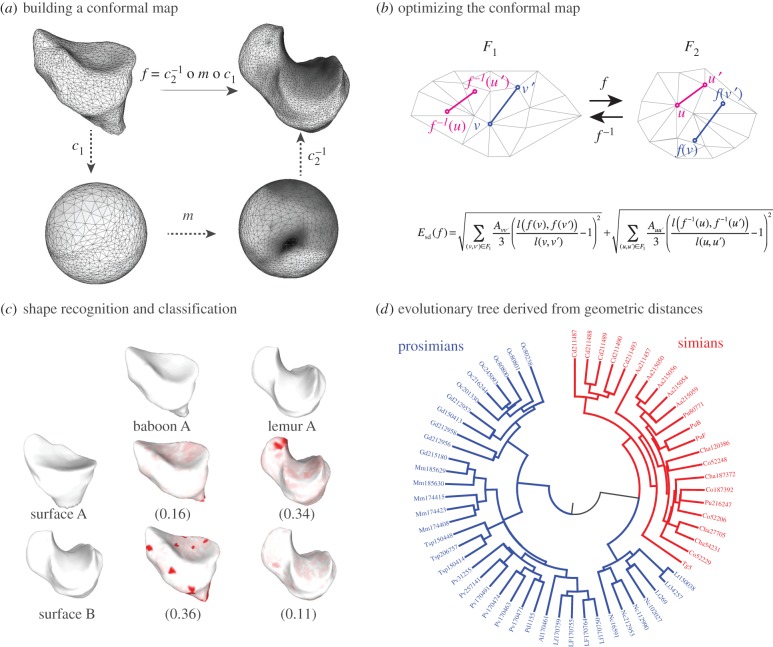
Figure 1.

An optimal conformal map and its applications. (a) The comparison of two surfaces F₁ and F₂ relies on the existence of a map f between these surfaces. When the two surfaces are of genus zero, it is possible to construct f as a composition of three maps C₁, m and C₂, where C₁ and C₂ are conformal maps from the surfaces F₁ and F₂ to the sphere and m is a bijective conformal map of the sphere to itself. The key to our approach is that the group of conformal self-maps of the sphere is the well-understood group of Möbius transformations. As such, m is defined by six parameters that can be optimized to yield minimal distortion. (b) Distortion is computed as the sum of the stretching induced by f on all edges 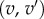in the mesh describing F₁, and of the stretching induced by 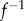on all edges 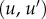in the mesh describing F₂. In the corresponding symmetric distortion energy E_sd(f), each edge is weighted by the areas of its adjacent triangles. The energy of the minimizing map defines a distance d_sd on the space of surfaces of genus 0. (c) Shape recognition is a natural application for the method described here. All surfaces shown here correspond to proximal metatarsal bones from baboons and lemurs. When the surface A is mapped onto the surfaces for baboon A and lemur A, the corresponding symmetric distortion distances d_sd are 0.16 and 0.34, respectively, identifying surface A as corresponding to a baboon. By contrast, surface B is closer to lemur A, and therefore corresponds to a lemur. Regions on the images with large stretching are coloured. (d) The unweighted pair group method with arithmetic mean (UPGMA) tree built from the distance matrix computed from a comprehensive comparison of all bones in database A clearly separates those bones into two categories, those from prosimians (left) and those from simians (right). This geometry-based categorization of the primates obtained from the metatarsal shapes can then be combined with other classifications to help understand their phylogeny. (Online version in colour.)