Fig. 2.

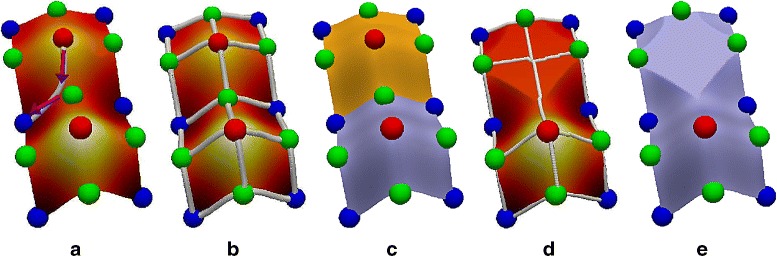
a Three types of criticalities in a Morse function defined on a smooth surface: maxima (red spheres), saddles (green spheres), and minima (blue spheres). An integral line originates at a minimum and terminates at a maximum. b The Morse-Smale complex is a partition of the domain into regions whose integral lines share a common source and destination critical point. The combinatorial structure of the Morse-Smale complex is a graph whose arcs are incident on an maximum-saddle or a saddle-minimum pair. c The descending manifold of a maximum is the region defined by the integral lines that converge to it. d The Morse-Smale complex may be simplified by local modification of the function resulting in the cancellation of a pair of critical points that are adjacent in the combinatorial structure. e After simplification, the descending manifold of the maximum that is adjacent to the canceled saddle expands to include the descending manifold of the canceled maximum