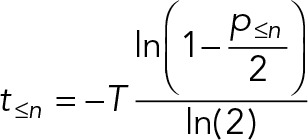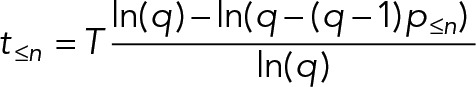Box 2.

If the ergodic assumptions are met, the timings of a series of stage-to-stage transitions in a cyclical process can be calculated using the following equations (derivations shown in the Supplemental Appendix).

For cycles with no offspring (cycles not linked with division events), (1) where t≤n is the time spent in stages up to and including stage n of the cycle, T is the time taken for one complete cycle, and p≤n is the proportion of cells observed in stages up to and including stage n of the cycle.

For cycles with two offspring (binary fission), (2)

For cycles with an arbitrary number of proliferative offspring (multiple fission, or a chance of terminal differentiation), (3) where q is the number of proliferative offspring per division.

For ergodic analyses based on classification of cells based on discrete features, p≤n is the proportion of cells that match the required features for that stage or any earlier stage of the cycle.

For ergodic analyses based on continuously varying features of cells, p≤n = r/k, where r is the rank position of that cell through the cycle and k is the total number of cells measured. Any set of continuously varying features, selected based on previous knowledge of the cycle, can be used to determine the rank position of the cell through the cycle.