A mechanistic in silico model predicts mitotic events and effects of perturbation in budding yeasts belonging to Ascomycota and Basidiomycota. The model identifies distinct pathways based on the population of cytoplasmic microtubules and cortical dyneins as determinants of nuclear and spindle positioning in these phyla.
Abstract
High-fidelity chromosome segregation during cell division depends on a series of concerted interdependent interactions. Using a systems biology approach, we built a robust minimal computational model to comprehend mitotic events in dividing budding yeasts of two major phyla: Ascomycota and Basidiomycota. This model accurately reproduces experimental observations related to spindle alignment, nuclear migration, and microtubule (MT) dynamics during cell division in these yeasts. The model converges to the conclusion that biased nucleation of cytoplasmic microtubules (cMTs) is essential for directional nuclear migration. Two distinct pathways, based on the population of cMTs and cortical dyneins, differentiate nuclear migration and spindle orientation in these two phyla. In addition, the model accurately predicts the contribution of specific classes of MTs in chromosome segregation. Thus we present a model that offers a wider applicability to simulate the effects of perturbation of an event on the concerted process of the mitotic cell division.
INTRODUCTION
Mitosis is a fundamental cellular process that enables faithful transmission of genetic material to the subsequent generation in eukaryotes. This process is well coordinated and requires the cumulative effort of several macromolecular machineries, including the centromere–kinetochore complex, the mitotic spindle, microtubule organizing centers (MTOCs), molecular motors, and microtubule-associated proteins (MAPs). The foundation for this process of chromosome segregation is provided by a specialized chromatin structure, the centromere, upon which 60–80 proteins assemble to form the kinetochore (KT). The KT connects centromeric chromatin to the mitotic spindle. The mitotic spindle, nucleated by MTOCs, is a bipolar array of microtubules (MTs) that provides the force required to segregate chromosomes. This mitotic spindle is synergistically modulated by motor proteins (Mallik and Gross, 2004), the plus end–directed kinesins and the minus end–directed dyneins, and MAPs, which dynamically alter the rate of MT stability. The unequal rate of MT polymerization and depolymerization provides the push–pull forces that mediate poleward movement of segregated chromosomes into two daughter cells. Apart from requiring the assembly of the segregation machinery on the centromere and push–pull forces to enable chromosomes to segregate, proper spindle positioning and orientation is crucial for carrying out faithful segregation of chromosomes (Segal and Bloom, 2001; Kusch et al., 2002).
In most organisms, MTs are largely localized to the cytoplasm until spindle formation begins during mitosis. These cytoplasmic MTs (cMTs) emanate from either multiple cytoplasmic MTOCs, as in metazoans, or from a single nuclear envelope (NE)-embedded MTOC, as in the budding yeast Saccharomyces cerevisiae. The cMTs, along with motor proteins, influence nuclear positioning and movement (Lee et al., 2000; Fink et al., 2006; Ten Hoopen et al., 2012). On the onset of mitosis, cMTs reorganize themselves to form the mitotic spindle between the two poles (spindle pole bodies [SPBs] in yeast or centrosomes in metazoans). The less dynamic minus ends of MTs are anchored to the SPBs, while the more dynamic plus ends radiate outward to facilitate interactions with other cellular components. Some of these MTs interact with KTs to become KT MTs (kMTs) and provide the pulling force on chromosomes during anaphase. Cytoplasmic (astral) MTs make contact with the cell cortex, aiding in spindle positioning, while interpolar MTs (ipMTs) are formed when the plus ends of MTs originating from opposite poles interact via sliding, resulting in an antiparallel array at the midzone. The combination of pushing force provided by ipMTs on SPBs along with the pulling force from kMTs and cMTs aids in segregation during anaphase.
The spindle positioning is not only crucial for proper chromosome segregation but also defines the site of division. In general, the spindle is positioned centrally in the dividing cell, and thus a mother cell gives rise to equal-sized daughter cells by the fission mode of division. While most organisms undergo this type of division, a few show variations in spindle positioning and hence give rise to cell polarity (Horvitz and Herskowitz, 1992; Neumuller and Knoblich, 2009). This type of division is mostly observed during developmental stages of multicellular organisms and in stem cells (Knoblich, 2008; Neumuller and Knoblich, 2009). Budding yeasts also undergo a similar unequal cell division, in which the site of division is defined before spindle positioning (Fraschini et al., 2008). A number of studies have been carried out to identify the factors that affect the dynamics of spindle positioning. Some of these regulatory factors are shown to be different between budding yeasts and multicellular organisms (Fraschini et al., 2008; Neumuller and Knoblich, 2009).
The process of chromosome segregation during budding has been well studied in S. cerevisiae and Candida albicans, both belonging to the fungal phylum Ascomycota. Recently these processes were studied in another phylum of fungi, Basidiomycota, represented by the yeasts Cryptococcus neoformans and Ustilago maydis. Although these organisms belong to two major fungal phyla and divide by budding, a striking variation is observed regarding the site of nuclear division that takes place in the mother cell in ascomycetes but in the newly budded daughter cell in basidiomycetes (Heath, 1980; Straube et al., 2005; Gladfelter and Berman, 2009; Kozubowski, Yadav, et al., 2013). In ascomycetes, the nucleus moves close to mother–daughter cell junction (neck) and divides into two equal halves. One half then moves to the daughter cell, and the other half is retained in the mother cell. In contrast, the nucleus moves completely to the daughter cell before division in basidiomycetes. Nuclear division takes place in the daughter cell, after which a divided nuclear mass moves back to the mother cell, while the other half is retained in the daughter cell. To address the molecular basis for this observed variability in mitosis between these yeast species, we first developed a common computational model that was subsequently modified to simulate the fungal phylum–specific nuclear dynamics during mitosis in ascomycetes or basidiomycetes. Mitosis has been studied extensively in several ascomycetous yeasts. To begin with, we established a computational model with available parameters that are well characterized for ascomycetes and then introduced varying parameters measured in vivo for both ascomycetes and basidiomycetes to develop two independent models. These models predict that cMT bias is required for directional nuclear movement in both ascomycetes and basidiomycetes. Both the models also accurately simulate the altered conditions that prevail during mitosis upon treatment of cells with various MT-specific depolymerizing drugs. We conclude that the models developed in this study offer a wider application toward understanding the consequences of not only short-lived mitotic events but also the consequences of small perturbations in the entirety of the mitotic cycle.
RESULTS
Generation of a computational model that replicates in vivo parameters of mitotic events
To model mitosis in budding yeast, we considered simplified versions of several cellular components known to play a role in chromosome segregation, including 1) SPB/MTOCs; 2) the centromere–KT complex; 3) cohesin complexes connecting sister chromatids before anaphase; 4) the MT network consisting of kMT, ipMT, and cMT; 5) cell cortex and cortical dyneins modulating cMT dynamics; and 6) kinesins involved in sliding overlapping ipMTs (Figure 1, A and B, and Table 1). The mother cell was considered an ellipsoid, while the nucleus was considered a spherical object placed randomly within the mother cell at the onset of simulations. To mimic the experimental scenario, we resorted to the same geometrical parameters of the mother cell as observed in our experiments (Table 1). Budding was initiated at a random location on the surface of the mother cell growing at the experimentally observed growth speed. MTs were modeled as straight filaments, and MT dynamics was replicated by incorporating stochastic switching between growing (lengthening) and shrinking (shortening) states by using standard computational techniques (see Materials and Methods). The cell cortex was taken as a rigid wall that resists free polymerization of the cMTs by applying a resistive force at the cMT tip. During mitosis, cortically anchored dynein motors that walk toward the minus end of the cMT generate a pulling force on the SPB and provide directional movement of the nucleus/SPB toward the cMT tip (Figure 1, A and B; see Materials and Methods for details). It is widely believed that cMT–cortex interactions play a vital role in nuclear migration in yeasts during mitosis (Carminati and Stearns, 1997; Adames and Cooper, 2000; Baumgartner and Tolic, 2014). We incorporated the idea of asymmetric loading of different protein molecules between the SPBs to ensure a biased nucleation of the cMTs in the model (Markus et al., 2012). Because we sought to understand the difference between the steady-state positioning of the spindles in ascomycetes and basidiomycetes, we ignored their instantaneous dynamics in this particular study.
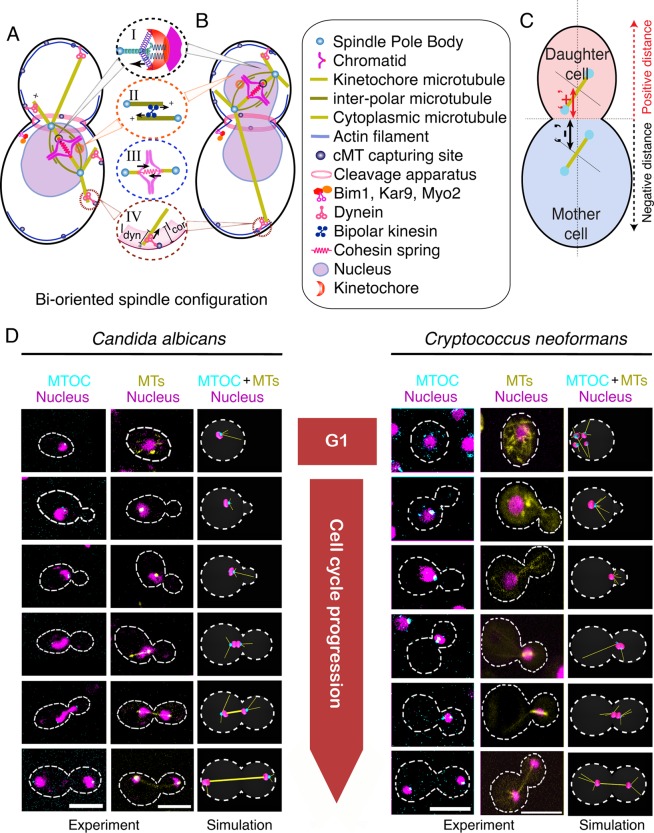
FIGURE 1:
Model development to study mitotic progression in ascomycetes and basidiomycetes. (A and B) Schematic of biorientation of chromosomes that occurs within (A) the mother cell in C. albicans and (B) the daughter cell in C. neoformans. Various forces are responsible for proper biorientation in both these organisms and are depicted in detail as follows: Depolymerization of kMTs at the KT enables poleward movement of chromosome (circle I). KTs interact with kMTs through spring-like attachments that regulate kMT dynamics. MT depolymerization at the KT pulls chromosomes toward the SPB. Before anaphase, this poleward force is countered by the sliding force generated by the plus end–directed kinesins acting along the ipMTs (circle II) and the cohesive force between the sister chromatids, which is considered as a spring between sister chromatids (circle III). cMTs interact with the cell cortex, where dynein pulls SPBs toward the cortex (circle IV). (C) The representative sign convention for labeling the spindle distance from the neck. (D) Cell cycle phase–specific dynamics of nucleus, MTOCs, and MTs in ascomycetes (C. albicans) and basidiomycetes (C. neoformans) was monitored by imaging a GFP-tagged component of MTOC or MTs along with nuclear dynamics, represented by DAPI-stained nuclei in C. albicans and mCherry-tagged histone H4 in C. neoformans. In C. albicans, a single MTOC, visible in unbudded cells, forms two active SPBs during S phase (small budded cells). The duplicated SPBs then migrate away from each other to establish a bipolar spindle (∼1.2 μm) in the mother cell during metaphase (large budded cells). In C. neoformans, multiple foci of MTOCs are observed at the beginning of the cell cycle. Observed MTOC foci merge together toward the onset of mitosis, forming an active SPB. After duplication, the SPBs migrate into the daughter bud and then establish a bipolar spindle evidenced by an increase in the distance (∼1.6 μm) between the SPBs. The nucleus, MTOCs, and MTs are false colored as magenta, cyan, and yellow, respectively. Scale bars: 5 μm.
TABLE 1:
Various parameters used to develop the model.
| Abbreviation | Meaning | Value for ascomycetes | Value for basidiomycetes | Reference |
|---|---|---|---|---|
| NKT | Number of KTs in haploid cell | 16 (S. cerevisiae) | 14 (C. neoformans) | Our experiment |
| NcMT | Number of cMTs | 4 | ∝4πrMTOC2 | Kosco et al., 2001 |
| acell, bcell, ccell | Dimension of the cell | 2.5–3.0 μm | 2.50–3.0 μm, | Our experiment |
| lcor | Width of cortex | 0.2 μm | 0.2 μm | Rodal et al., 2005 |
| Kcor | Spring constant of the cortex | 5.0 pN/μm | 5.0 pN/μm | This study |
| rnu | Initial radius of the nucleus | 1.0 μm | 1.0 μm | Our experiment |
| rSPB | Radius of single SPB | 0.125 μm | 0.125 μm | Seybold and Schiebel, 2013; Lee et al., 2014 |
| rKT | Radius of single KT | 0.05 μm | 0.05 μm | Haase, Mishra, et al., 2013 |
| vg, vs | Growth, shrinkage velocity of MT | 6.4 μm min−1, 26.6 μm min−1 | 10.4 μm min−1, 28.6 μm min−1 | Fink et al., 2006; Finley et al., 2008 |
| fc, fr | Catastrophe, rescue frequency of MT | 0.34 min−1, 0.02 min−1 | 1.0 min−1, 0.02 min−1 | Fink et al., 2006; Finley et al., 2008 |
| fs | Stall force of MT | 1.7 pN | 1.7 pN | Dogterom and Yurke, 1997 |
| fsdyn | Force produced by single dynein | 1.0 pN | 1.0 pN | Muller et al., 2008; Soppina et al., 2009 |
| λdyn | Density of dynein per unit length per MT | 6.0 /μm | 6.0/μm | Civelekoglu-Scholey et al., 2006 |
| λipMT | Density of ipMT motor per unit length | 1.0 /μm | 1.0/μm | Civelekoglu-Scholey et al., 2006 |
| ƒipMT | Force produced by single ipMT motors | 1.0 pN | 1.0 pN | This study |
| ηcell | Viscosity of cytoplasm | 5.0 pN s/μm2 | 5.0 pN s/μm2 | Civelekoglu-Scholey et al., 2006 |
| ηnu | Viscosity of nucleoplasm | 10.0 pN s/μm2 | 10.0 pN s/μm2 | Civelekoglu-Scholey et al., 2006 |
| ηNE | Viscosity of NE | 10.0 pN s/μm2 | 10.0 pN s/μm2 | Civelekoglu-Scholey et al., 2006 |
| Kcohesion | Spring constant of the cohesion springs | 0.1 pN/μm | 0.1 pN/μm | Joglekar and Hunt, 2002 |
| KC | Spring constant of the KT–kMT attached springs | 10.0 pN/μm | 10.0 pN/μm | Civelekoglu-Scholey et al., 2006; Sau et al., 2014 |
| Kfibrils | Spring constant of the KT fibrils | 5.0 pN/μm | 5.0 pN/μm | Civelekoglu-Scholey et al., 2006; Sau et al., 2014 |
| C | Repulsion strength of KTs | 1.0 pN/μm | 1.0 pN/μm | This study |
It is observed that KTs remain clustered in yeasts during mitosis (Jin et al., 2000; Anderson et al., 2009; Kozubowski, Yadav, et al., 2013; Varoquaux et al., 2015). Hence, to avoid overlapping of individual KTs, each KT was modeled to have a hard-core excluded volume. Assembly of sister KTs occurred immediately after centromere replication. To simplify the model, we assumed newly assembled sister KTs were captured instantaneously. It is observed that, in yeasts, the KTs always remain attached to the SPB during mitosis, except for a few minutes during chromosome duplication (Tanaka et al., 2005, 2010; Tanaka and Tanaka, 2009; Gandhi et al., 2011). Compared with mammalian cells, the KT capture process in ascomycetes occurs faster. Considering that nuclear migration per se is a much slower process than KT capture, instantaneous capturing of KTs is not expected to change our model prediction. At the ipMT overlap region, plus end–directed molecular motors slide the MTs apart, generating a pushing force on the SPBs (Kapoor and Mitchison, 2001; Marco, Dorn, et al., 2013). The kMT–KT interaction is mediated by spring-like KT fibrils (McIntosh et al., 2008). Before anaphase, two opposing forces on the KTs, an outward pulling force toward SPBs, driven by motor proteins and depolymerizing kMTs, and an inward cohesive force between the sister chromatids due to cohesin proteins must be balanced to satisfy the spindle-assembly checkpoint and subsequent entry to anaphase. For maintaining the experimentally observed separation between the KT cluster and SPBs, a length-dependent catastrophe of kMTs was incorporated (Foethke et al., 2009; Sau et al., 2014).
The nuclear mass always divides close to the mother bud junction in budding yeasts
The nuclear division or mitotic spindle formation in ascomycetes takes place in the mother cell, whereas it occurs in the daughter cell in basidiomycetes (Heath, 1980; Straube et al., 2005; Gladfelter and Berman, 2009; Kozubowski, Yadav, et al., 2013; Figure 1D, fourth and fifth row). Although the spindle positioning in ascomycetes is a relatively well-studied process (Piatti et al., 2006; Merlini and Piatti, 2011), very little is known about the same in basidiomycetes. We used fluorescence microscopy to understand the spindle and nuclear dynamics simultaneously in these two classes of yeasts. In ascomycetes, represented by S. cerevisiae and C. albicans henceforth, only one visible interphase MTOC serves as the SPB during mitosis (Figure 1D; Segal and Bloom, 2001). In contrast, among basidiomycetes, henceforth represented by C. neoformans and U. maydis, several MTOCs were seen spread throughout the cytoplasm during interphase (Figure 1D; Straube et al., 2003). These MTOCs subsequently coalesced to form an active SPB during mitosis.
In premitotic cells, SPBs are localized at a constant distance from each other after duplication, which segregates rapidly during the onset of mitosis (Figure 1D). The distance from the center of the mitotic spindle to the neck was measured in a number of cells (n = 30) during metaphase and early anaphase. The neck was taken as the origin, and the distance was marked as (+) or (−) for the presence of the spindle in the daughter cell or mother cell, respectively, during mitosis (Figure 1C). The net average neck–spindle distance for ascomycetes (−1 ± 0.22 μm) was found to be similar in basidiomycetes (+0.84 ± 0.23 μm). Thus the nucleus was found to be positioned close to the neck during mitosis, irrespective of the dynamics of nuclear movement in premitotic stages. In other words, the cellular machinery divides the nuclear mass into two equal halves across the neck in a well-conserved manner, irrespective of its earlier dynamics. The data obtained from these experiments and previously published results (Table 1) were incorporated into the universal model for mitosis described above to yield two working models, one each for ascomycetes and basidiomycetes (Figure 1, A and B, and Supplemental Videos 1 and 2).
Nuclear/spindle dynamics depends on the number of cMTs and dynein activity
Having developed these models, we probed for the underlying variation in nuclear migration observed between ascomycetes and basidiomycetes. Differential migration patterns and a large deformation of the nucleus during migration suggested that the magnitude of force pulling SPBs toward the bud is greater in basidiomycetes compared with ascomycetes (Straube et al., 2005; Fink et al., 2006; Kozubowski, Yadav, et al., 2013). The larger force generated could either be due to an increased population of cMTs and/or a higher dynein activity at the cortical region. It is widely believed that ascomycetes nucleate ∼4 cMTs (Kosco et al., 2001), whereas the number of cMTs in basidiomycetes is unknown. A previous study using U. maydis showed that the number of MTs in this organism is 10–15, indicating a higher number of cMTs in basidiomycetes (Straube et al., 2003).
Considering a conserved cMT–cortex interaction, our model revealed that the size of the cMT population must be more than eight for producing sufficient force to pull the nucleus into the daughter cell (Figure 2A). Assigning the number of cMTs as four for ascomycetes and eight for basidiomycetes, simulations predicted the mean distances between the neck and the spindle as −0.90 and +0.83 μm, respectively. These values are close to the experimental measurements (Figure 2B). Further, an increase in the density of cortical dyneins engaged in pulling the cMTs also provided enough pulling force for the migration of the nucleus into the daughter cell in the basidiomycetes model when other parameters were kept constant (Figure 2C). To test the model’s prediction of requiring a greater number of cMTs in basidiomycetes for migration of the nucleus into the daughter cell, we counted the cMTs in C. albicans (Figure 2D) and C. neoformans (Figure 2E; see Materials and Methods). Our experiments revealed that C. neoformans has an approximately at least two times higher number of cMTs than C. albicans (Figure 2, D–F). It was observed that approximately six to 15 cMTs formed a dense mesh-like network in C. neoformans, with an average number of cMTs per cell being approximately nine (Figure 2F), while each C. albicans cell has three to five cMTs with an average of approximately four cMTs per cell (Figure 2F). The results presented above confirm the importance of cMT and dynein in positioning the spindle. Disruption of any of these components leads to severe mitotic defects (Markus and Lee, 2011; Laan et al., 2012; Xiang, 2012; Best et al., 2013). Thus our model prediction, supported by experimental validation, confirms that an increased number of cMTs is required for migration of the nucleus/SPB into the daughter cell.
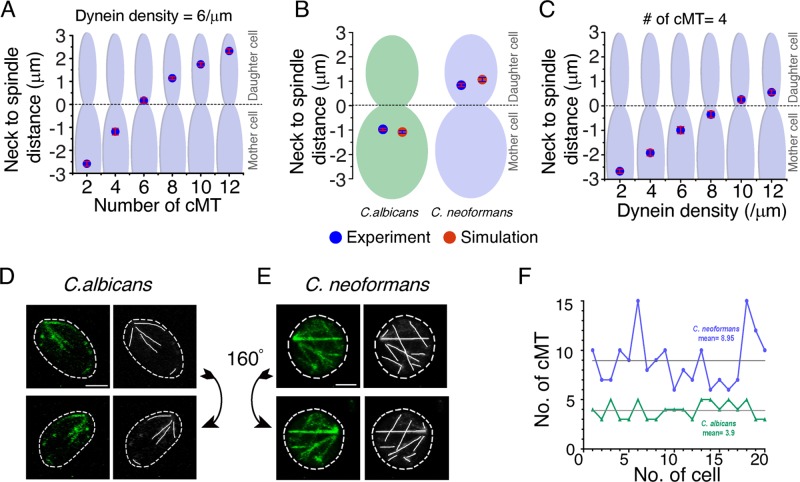
FIGURE 2:
Dependence of nuclear migration on the number of cMTs and dynein activity in ascomycetes and basidiomycetes. (A) In silico measurements of the neck to spindle distance upon altering cMT numbers per cell during mitosis. We observed that, for a fixed density of cortical dynein, a higher number of cMTs leads to a deeper penetration of the spindle into the daughter cell (bud). With four cMTs, the observed spindle distance from the neck is close to −1.0 μm, which is similar to that observed in ascomycetes. As we increase the number of cMTs, the spindle moves closer to the neck, and when there are six cMTs, the spindle just crosses over into the daughter cell. The spindle is strongly pulled and moved deep into the daughter cell when the number of cMTs is eight or more, resembling what is observed in experiments. (B) Mean distance of the spindle from neck is plotted as observed in simulation (n = 100) and experiments (n = 30) for both C. albicans and C. neoformans. Experimental measurements were carried out in a strain that had MTOCs tagged with GFP. Differential interference contrast was used as a reference point for calculating spindle mid to neck distance. The mean distance of the spindle from the neck in C. albicans is estimated as −1.0 ± 0.22 μm in experiments, while our in silico model prediction with four cMTs turns out to be −1.0 ± 0.02 μm. On the other hand, the spindle to neck distance in C. neoformans with eight or more cMTs is found to be +0.84 ± 0.23 μm and +1.0 ± 0.05 μm from experiments and in silico measurements, respectively. (C) The spindle migration can also be affected by an alternative pathway involving cortical dyneins. An increase in the cortical dynein density for a fixed number of cMTs results in similar nuclear dynamics obtained previously by altering the cMT number. SEM is shown in red bars. (D and E) C. albicans (YJB12856) and C. neoformans (CNVY109) strains expressing Tub1-GFP were used to monitor and estimate cMTs. To rule out false positives in counting, we used high-resolution three-dimensionally rendered images to trace cMTs before estimation of their numbers. The cMTs in all stacks were taken into consideration. Two different views over the y-axis (0°, top panels; 160°, bottom panels) of the three-dimensionally rendered images are shown to improve the visibility of cMTs that may be masked by others in a given orientation. Scale bar: 2 μm. (F) The cMTs were counted in a large number of cells of C. albicans and C. neoformans. These values were plotted, and the calculated mean of cMTs per cell in each case is represented by a gray line. C. neoformans was found to contain six to 15 cMTs per cell, with an average of 8.95, while C. albicans was found to contain three to five cMTs per cell, with an average of 3.9.
A biased “search and capture” by the cMTs is required for proper nuclear migration and spindle alignment
Next we analyzed whether the nuclear migration was governed by a random or polarized nucleation of cMTs. To test this, we performed simulations on both the models, keeping either an unbiased or a biased nucleation toward the daughter cell (Figure 3). The directional movement of the nucleus was impaired for an unbiased nucleation of cMTs, but the metaphase spindle length was found to be independent of cMT bias (Figure 3, A–D, and Supplemental Figure S1 and Videos 3 and 4). In both the cases, however, a biased dynamics of cMTs was crucial for proper nuclear migration (Figure 3, C and D, and Supplemental Figure S1). The resulting spindle–neck distances were found to be similar to the experimental values. Basidiomycetes showed some directional movement of the nucleus even in the absence of biased nucleation, which we attribute to a higher number of cMTs when compared with ascomycetes (Figures 2F and 3D). An unbiased cMT dynamics also failed to align the spindle with the mother–daughter cell axis, adding to the severity of the defect in these cases (Figure 3, E and F).
FIGURE 3:
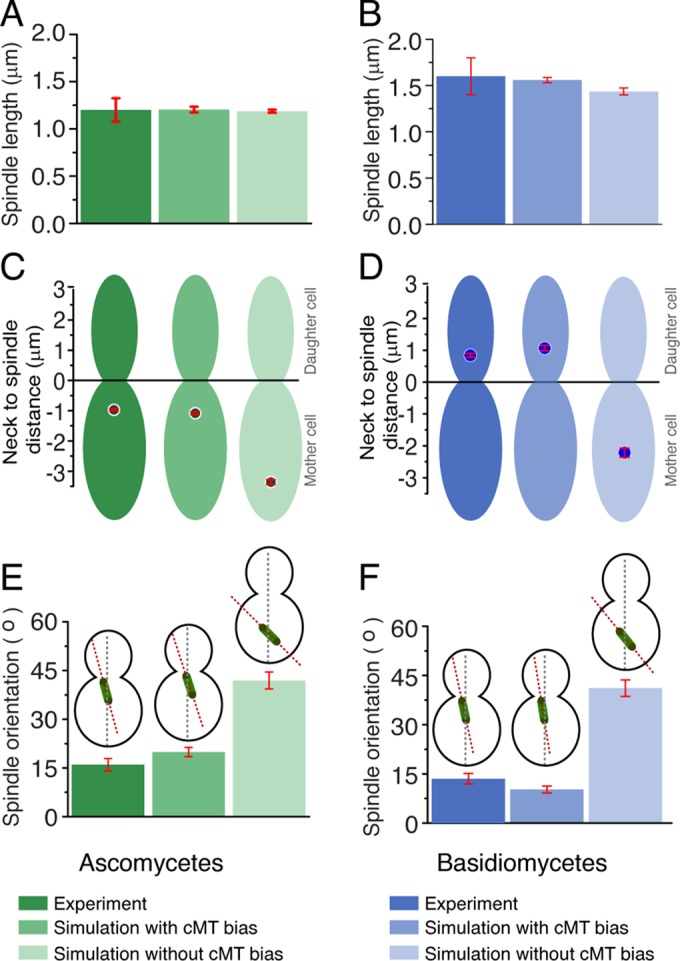
Biased vs. unbiased MT dynamics in maintaining spindle length, position, and orientation in ascomycetes and basidiomycetes. (A and B) The spindle length at metaphase was calculated in the model with biased or unbiased cMTs for both C. albicans and C. neoformans. Experimental measurements were carried out during mitosis to measure the spindle length. The model predicts that the spindle length at metaphase remains unaltered irrespective of cMT bias, as experimentally observed. (C and D) Neck to spindle distance is measured with or without cMT bias, while simultaneously comparing it with experimental data (wild type). With unbiased cMT, the spindle often failed to move to the predefined spatial positions in both ascomycetes and basidiomycetes. The spindle–neck mean distance changes from –1.0 to –3.35 μm during unbiased nucleation in ascomycetes. The spindle to neck mean distance in basidiomycetes, changes from +1.0 to –2.2 μm during unbiased nucleation. (E and F) Orientation of the spindle is calculated by measuring its tilt with respect to the mother–daughter cell axis. Unbiased cMT dynamics result in a larger angular orientation (∼42° in ascomycetes and ∼41° in basidiomycetes), with the mother–daughter cell axis reflecting the misaligned spindles for unbiased cMT dynamics. For biased cMT dynamics, the spindle aligned with the mother–daughter cell axis, and the angular orientation is measured as ∼21° ± 2.1° for ascomycetes and ∼10.25° for basidiomycetes. Red bars indicate SEM.
Clearly, biased cMTs produce a directed force on the nucleus/SPB, whereas uniformly nucleated cMTs generate force without any preferred directionality that therefore often fails to move the nucleus/SPB to the predefined position. Many studies revealed that a cortical actin-dependent mechanism, known as the “Kar9 pathway,” utilizes a myosin-V, Myo2-based machinery to guide the plus ends of cMTs along the cortex toward the neck at the early stage of the cell cycle (Beach et al., 2000; Yin et al., 2000). Reports also suggest that asymmetric loading of Kar9 at the SPB can produce a chemical cue that leads to a biased nucleation of cMTs toward the neck (Liakopoulos, Kusch, et al., 2003; Cepeda-Garcia et al., 2010). The current model exploits these results, providing an additional line of evidence for the same.
The model accurately reproduces experimental outcomes of various drugs affecting MT dynamics
Next we tested the model by simulating the effects of two drugs that are known to affect the dynamics of specific classes of MTs in vivo. To depolymerize all MTs present in the cell, the MT-depolymerizing drug nocodazole was used, whereas methyl benzimidazole carbamate (MBC; Akera et al., 2012) was used to disrupt ipMTs specifically. The depolymerizing kinetics for nocodazole treatment was simulated by increasing the catastrophe frequency of all the MTs in the model. Similarly, to simulate the effect of MBC, ipMT catastrophe was increased without altering the dynamics of cMTs or kMTs.
Our model accurately simulates the effect of nocodazole treatment, resulting in shorter spindles that failed to move to the bud (Figure 4 and Supplemental Videos 5 and 6). For both ascomycetes and basidiomycetes, the spindle length was drastically shorter than untreated cells (Figure 4, A and B). We also observed that the spindle is mispositioned and misaligned, as depicted by the higher mean values for the neck to spindle distance and a higher spindle orientation angle (Figure 4, C–F). Misaligned spindles are identified as those making angles greater than 30° with the mother–daughter axis, while mispositioned spindles position themselves farther than 1 μm away from the neck. Simulations for higher nocodazole concentration were achieved by increasing the catastrophe frequency of the MTs (8–12/min), resulting in shorter MTs. Under these circumstances, initial MTOC and KT clustering in basidiomycetes were highly affected due to altered cMT dynamics (Supplemental Figure S2). These simulated results correlated with the experimental results and accurately corroborated the in vivo observation of KTs failing to cluster upon nocodazole treatment, as reported previously (Kozubowski, Yadav, et al., 2013).
FIGURE 4:
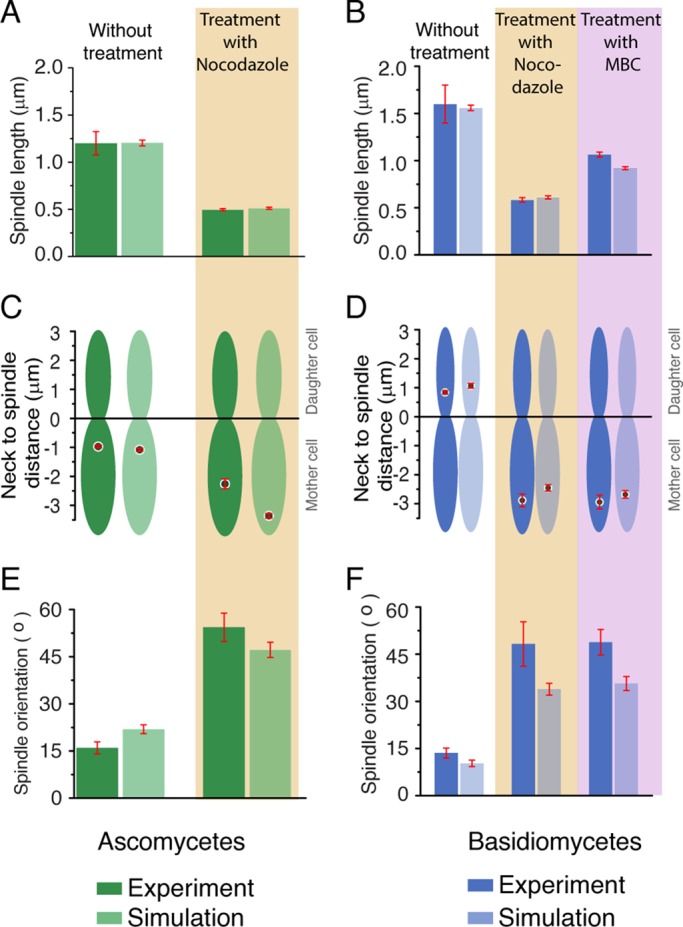
Comparison of in vivo and in silico results upon altering dynamics of MTs in ascomycetes and basidiomycetes. (A and B) Metaphase spindle lengths upon treatment with nocodazole or MBC are plotted for ascomycetes and basidiomycetes along with the unperturbed (dimethyl sulfoxide [DMSO] control) numerical and experimental data. For ascomycetes, we observed that, upon nocodazole treatment, the spindle length becomes ∼0.50 ± 0.04 μm, which is in accordance with our model prediction ∼0.52 ± 0.01 μm. Similarly, in basidiomycetes, the spindle length is reduced to ∼0.61 μm from its wild-type spindle length of ∼1.66 μm. This is in accordance with the experimental value 0.62 ± 0.04 μm. For MBC treatment, in basidiomycetes, the spindle length is shortened to 0.9 μm from its native value of 1.6 μm. This in silico result is in agreement with the experimental data for basidiomycetes as shown. (C and D) Measurements of spindle to neck distances for ascomycetes (with nocodazole) and basidiomycetes (either with nocodazole or MBC) revealed the inability of the spindles to move to their unperturbed spatial locations. The spindle always remained in the mother cell with an increased mean distance (∼ −2.7 μm for nocodazole) from the neck compared with its wild-type value (∼ −1.0 μm) in ascomycetes. In basidiomycetes, the spindle failed to move to the bud, and always remained in the mother cell during either nocodazole or MBC treatment. (E and F) The spindle orientation in the presence or absence of drugs was measured, and it was found to misalign with mother–daughter cell axis, as shown by the higher spindle orientation angle in both cases. Red bars indicate SEM.
After treatment with MBC, the spindle length was found to be shortened in basidiomycetes (Figure 4B and Supplemental Video 7). This effect was less drastic as compared with nocodazole, as the spindle length was longer for MBC-treated cells. Similar to the nocodazole treatment, mispositioned and misaligned spindles were also observed (Figure 4, D and F) when treated with MBC. These results suggest that the role of ipMTs is not crucial for SPB separation, but they are required for spindle migration and orientation in basidiomycetes. The effect of MBC treatment could not be examined in ascomycetes, because MBC does not affect the cell cycle events of C. albicans, as reported earlier (Finley and Berman, 2005). Taken together, the consequences of experimental perturbation of various species of MTs on chromosome segregation are accurately simulated in the model. On the basis of these results, we conclude that the model developed is a robust one and can replicate the events observed in the in vivo experiments with high precision.
DISCUSSION
In this study, we describe a model that accurately simulates the events of mitosis in distantly related budding yeasts belonging to the phyla Ascomycota and Basidiomycota. We also sought to understand the basis behind the differences in mitotic events observed in these two phyla. A universal model was developed for the budding mode of division, following which mitotic events were simulated and modeled both for ascomycetes and basidiomycetes by obtaining parameters either from the literature or through experimental measurements. When this information was compared, we observed that variations in the MT organization, orientation, and dynamics account for most of the variations in mitotic events observed between these two classes of yeasts.
While making experimental measurements for basidiomycetes using C. neoformans, it was observed that, although the spindle migrates entirely to the daughter cell during mitosis, it is always positioned close to the neck at metaphase. Similarly in ascomycetes, the nucleus moves very close to the neck, where the division takes place during mitosis. This indicates that the site of nuclear division with respect to the site of cytoplasmic division remains conserved in these two classes of yeasts in spite of the other observed differences. In metazoans, fission yeast, and filamentous forms of many fungi (including the ones studied here), the site of nuclear division defines the site of cytoplasmic division (Balasubramanian et al., 2000; Guertin et al., 2002; Wang et al., 2003; Gladfelter and Berman, 2009). Hence cells seem to have developed a mechanism, as nuclear division takes place close to the predefined cell cleavage site in budding yeasts. The interaction of MTs with septin proteins and other cleavage elements plays a determinant role in this process (Castillon et al., 2003; Rodal et al., 2005). Indeed, several reports in S. cerevisiae have shown that positioning of the spindle close to the neck is important for accurate chromosome segregation (Piatti et al., 2006; Merlini and Piatti, 2011). In the absence of proper alignment and positioning of the mitotic spindle, the spindle positioning checkpoint (SPOC) is activated in these cells delaying chromosome segregation (Piatti et al., 2006; Fraschini et al., 2008). Hence this conserved distance observed between the neck to the spindle is possibly due to the SPOC activity that uses cMTs to monitor the location of the spindle in dividing cells (Moore et al., 2009). Such a strict positioning of the spindle in basidiomycetes might reflect the conservation of the regulatory process.
The cytoskeletal elements, primarily MTs and their accessory network of proteins, have been shown to influence nuclear migration (Hwang et al., 2003; Straube et al., 2003; Martin et al., 2004; Fink et al., 2006; Gladfelter and Berman, 2009; Markus et al., 2012; Kozubowski, Yadav, et al., 2013). Our model revealed that nuclear migration toward the daughter cell would occur only if cMTs organized themselves in a biased manner in the direction of the newly emerging daughter cell. This was found to be applicable for both ascomycetes and basidiomycetes. Previously, several reports indicated that actin and other cytoskeleton elements reorganize during budding in yeasts, giving rise to cell polarity (Pruyne and Bretscher, 2000a, b). We show here that polarized MT nucleation plays an important role during the process of mitosis. This hypothesis is supported by experimental observations suggesting that an asymmetric recruitment of proteins (Myo2, Bim1, Kar9, etc.) may guide the cMTs to grow and stabilize toward the emerging daughter cell (bud; Miller et al., 1998; Miller and Rose, 1998; Yin et al., 2000; Huisman et al., 2004; Markus et al., 2012). Model simulations also predicted that at least eight cMTs are required to provide the necessary force to migrate the entire nucleus to the daughter cell in basidiomycetes. This was in agreement with our experimental observations that show each C. neoformans cell nucleates an average of approximately nine cMTs. Thus a greater number of cMTs in basidiomycetes (∼9 cMTs/cell) as compared with ascomycetes (∼4 cMTs/cell) provides a larger pulling force on the SPB toward the emerging daughter cell, resulting in a deeper penetration of the SPB in basidiomycetes. However, our model also predicts a redundant pathway in which an increased activity (population) of dynein motors present at the cortical region of the daughter cell could also provide sufficient force to pull the nucleus/SPB into the bud.
The role of various MTs was determined by varying MT dynamics both by model simulations and by performing specific experiments, while scoring for the dynamics of the nuclear mass and SPBs through the progression of the cell cycle. The model predicted that disruption of all or only ipMTs results in the formation of short spindles without any nuclear movement toward the daughter cell. Experiments with depolymerizing drugs followed by measurement of the spindle length, neck to spindle distance, and the spindle axis revealed cells are arrested at the short-spindle stage. These experimental measurements, being in strong agreement with the model predictions, provide additional lines of validation for the developed models.
As our model can be used to simulate major transitions in mitosis, biological events spanning a short timescale can be incorporated to understand their global effects on the entire process of mitosis. Although we focused solely on the role of MTs in this study, the model can also be used to address other contributing factors and their roles among these systems. For example, using this model, we aim to further analyze the role of motor proteins during mitosis and to define their roles more specifically. However, this model also has certain limitations, which include consideration of only mechanical forces, absence of NE dynamics, and lack of regulation by the mitotic checkpoint. DNA replication was considered as an instantaneous process, and MT dynamics was taken as constant throughout the cell cycle, further adding to the model constraints. However, this model lays the foundation for follow-up work that will help create a more refined and comprehensive model. It is important to mention here that the above-mentioned limitations/assumptions do not affect the quantitative conclusions presented in this study. The predictive nature and robustness also remained unaltered when model parameters were varied within a permissible window. Nevertheless, a parallel set of pathways based on novel assumptions may exist that could produce results similar to the ones presented here.
In the present study, we developed a model to cover a large fraction of the mitotic cell cycle that is the first of its kind to our knowledge. We could successfully characterize different mitotic events, including the nuclear migration, spindle orientation, and spindle-length dynamics in a quantitative manner utilizing a holistic approach across two major fungal phyla. This type of systems biology approach to develop a predictive computational model may aid in identifying targets across human pathogenic yeasts for developing antifungal drugs.
MATERIALS AND METHODS
Model development
In this section, we describe the model variables and governing equations in a simplified configuration to explain the mitotic mechanics in ascomycetes and basidiomycetes (Figure 1, A and B).
Construction of mother and daughter cell
We consider the mother cell as an ellipsoid of dimensions acell, bcell, and ccell along the x, y, and z axes, respectively, whereas the nucleus is considered to be a sphere of radius rnucleus placed at a random location within the mother cell at the beginning of the simulation. In ascomycetes, the SPB is embedded into the NE (Kahana et al., 1995; Jaspersen and Winey, 2004), whereas in basidiomycetes, no active SPB is reported to exist in the early stages of mitosis. However, multiple MTOCs are found that wade along the nuclear surface in basidiomycetes (Straube et al., 2005; Fink et al., 2006; Yamaguchi et al., 2009). It has been observed that these MTOCs converge to a single mass during mitosis, leading to SPB activation (Straube et al., 2003). Formation of the bud can occur anywhere on the cell surface. We considered that the final volume of the bud is ∼80–90% of the mother-cell volume, as observed in our experiments. We chose the growth rate of the daughter cell in our model such that it reflects the experimentally observed scenario. Our model predicts that the growth rate of the bud does not play any significant role in spindle positioning (Supplemental Figure S3); however, cell size variation affects the spindle positioning (Supplemental Figure S4).
Modeling of cMT and cMT and cortex–based interaction
The SPB nucleates cMTs that interact with the cell cortex via dynein motors (Carminati and Stearns, 1997; Adames and Cooper, 2000; Ten Hoopen et al., 2012). MTs are modeled as straight filaments elongating with velocity vg and shrinking with velocity vs. Stochastic switching of MTs from a growing state to a shortening state and then the shortening state to the growing state occur with catastrophe frequency fc and rescue frequency fr, respectively (Mitchison and Kirschner, 1984). One can successfully simulate the dynamics of an MT using these four parameters. We assume that the cell cortex acts as a static wall that resists the growth of a cMT. The growth velocity of a cMT within the cortical region decreases as vg = vg0exp(−Kcorldyn/fs) (Dogterom and Yurke, 1997; Janson et al., 2003), where vg0 is the unconstrained growth velocity of an MT, Kcor is the stiffness of the cortex, ldyn is the length of penetration of the cMT tip within the cortex, and fs is the stall force per MT. Dyneins engage with the cMTs, growing within the cortical region of width lcor, to pull the SPB and the nucleus toward the cortex (Carminati and Stearns, 1997; Adames and Cooper, 2000; Lee et al., 2000; Ten Hoopen et al., 2012). We assumed that several proteins like Tem1, Bub2, Bfa1, Elm1, and Num1 assemble close to the cleavage apparatus at the neck during mitosis (Huisman et al., 2004; Rodal et al., 2005; Cuschieri et al., 2006; Baumgartner and Tolic, 2014). These protein molecules stabilize the cMTs and allow cMTs to interact with the cleavage apparatus (Castillon et al., 2003). To achieve stable cMTs, rescue frequency of the cMTs is adjusted as a function of the distance of the cMT tip from neck as fr(x) ∞ exp(−x/l),where x is the distance between the tip of the cMT and neck, and l is a constant that is of the size of the cleavage apparatus (∼0.2 μm). The pulling force due to the dyneins is calculated using the following expression:
|
|
Here ldyn is the penetration length of cMT within the cortical region, λdyn is the number of dynein motors engaged per unit length of the cMT, and fdyns is the magnitude of the force exerted by a single dynein motor. Summing fdyn over all the cMTs, we can estimate the total pulling force Fdyn on the SPB/nucleus. The cMTs also exert a net pushing force Fpush (∼1 pN) when the tip hits the cell periphery. Pushing force arises due to the polymerization of the cMT tip in contact with the cell cortex. To apply a bias to the cMTs, we explored several schemes, such as modulation of the dynamical parameters and differential cortical interaction between the mother and the daughter cells, independently.
Modeling KT and KT–MT interaction
During mitosis, KTs remain clustered and linked to SPBs through kMTs. To avoid any overlap among the KTs, we include inter-KT repulsion in a simplistic manner. Whenever two interacting KT spheres, each of radius rkt, penetrate each other, a repulsive force keeps them separate. For the sake of simplicity, the repulsive force is considered as a linear function of the extent of overlap. The total repulsive force on the ith KT can be estimated as
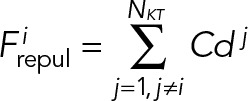 (2) (2)
|
Here C is a constant, NKT is the number of KTs present in the nucleus and dj is the maximum overlap length between the ith and the jth KT.
The dynamics of the kMT plus end plays a crucial role in positioning the KT in yeast (Gardner et al., 2008). We assume that kMTs remain attached to the KTs throughout mitosis (Westermann et al., 2007). The kMTs interact with the inner KT through spring-like KT fibrils (McIntosh et al., 2008). As the polymerizing kMT tip penetrates the KT, it applies a pushing force on the KT, namely, Fpoly= lpenKfibrils, where lpen is the length of penetration of the kMT tip within the KT, and Kfibrils is the effective spring constant of the KT fibrils. A depolymerizing kMT pulls the KT with a force Fdepoly= loutKc while trying to detach from the KT. Here lout is the separation between the kMT tip and the KT, and Kc is the force constant of the kMT–KT connecting springs (Wei et al., 2007; Powers et al., 2009). We calculate the total force acting between the SPB and KT as FSPB-KT= ∑(Fpoly + Fdepoly), where the sum over is the number of MTs interacting with a single KT. To maintain a constant distance between the SPB and the KT, we incorporated the notion of the length-dependent catastrophe of the kMT (Varga et al., 2006; Varga, Leduc, et al., 2009; Foethke et al., 2009; Sau et al., 2014), that is, catastrophe frequency of a kMT increases with its length lkMT as fc= hlkMT.
Modeling ipMTs
After the duplication of the SPB, overlapping ipMTs facilitate mechanical interaction between the SPBs. Due to the presence of kinesin 5 motors along the overlap (Kapoor and Mitchison, 2001; Marco, Dorn, et al., 2013), ipMTs tend to slide apart, essentially pushing the SPBs away from each other. The pushing force FipMT reads as
|
|
where loverlap is the total overlap length among all the ipMTs nucleated from the two SPBs, λipMT is the linear density of kinesin motors engaged along the ipMTs, and fipMT is the force produced by a single ipMT motor.
During SPB duplication, KTs detach from the kMTs and reattach right after successful duplication. We assume all the KTs are captured instantly by the MTs nucleated from the mother and the daughter SPB, such that chromosomes are bioriented. The actual capture process and achievement of the biorientation, though, are far more complex and occur over a finite timescale (Marco, Dorn, et al., 2013). In the present study, we ignore such details and focus on the spindle positioning and orientation during mitosis. It is noteworthy to mention that the KTs remain attached to the SPB throughout the cell cycle (except for 2–3 min during chromosome replication), and the average nuclear migration time is long (∼1 h). Thus it is safe to assume the KT capturing process is “instantaneous.” After chromosomal duplication, sister KTs remain attached to each other by cohesion springs. The cohesion springs, when stretched, generate tension between the sister KTs:
|
|
where Kcohesion is the spring constant of the cohesion springs and xKT is the separation between the sister KTs.
KTs always remain clustered in ascomycetes, whereas in basidiomycetes they are unclustered during interphase and each of them remains close to the NE in the beginning of mitosis. The KT clustering process ahead of mitosis was shown to be mediated by MTs (Kozubowski, Yadav, et al., 2013). Further, the clustering of the MTOCs and KTs occurs at the same time before mitosis (V.Y. and K.S., unpublished data). Hence, in this model, we assume a direct interaction between the MTOCs on the outer surface of the NE with the adjacent KTs present on the inner surface. All MTOCs in C. neoformans nucleate MTs in random directions and interact with each other via these MTs. If, by chance, a searching MT from one MTOC captures another MTOC, they migrate along the connecting MT toward each other and coalesce to form a unified MTOC, conserving the total volume. The number of MTs nucleated from the merged MTOC is proportional to its surface area. The “search and capture” of MTOCs continues until all MTOCs merge together to form a single SPB. Because MTs can bend, the search extends along the nuclear periphery. In this way, two MTOCs situated on the diametrically opposite ends of the nucleus can interact with each other. Because self-assembly of MTOCs is an MT-driven phenomenon, the efficiency of this process depends on the selection of the dynamical parameters that determine MT life cycles. For instance, a very small catastrophe frequency leads to long MTs, which are efficient in capturing distant MTOCs; however, misdirected MTs waste valuable search time while completing their life cycles. Similarly, a very large catastrophe frequency leading to short MTs is also inefficient in locating distant MTOCs (Supplemental Figure S2). Thus MT dynamics are tuned and optimized to assemble MTOCs within experimental time frames.
The equation of motion for KT, SPB, and nucleus can now be written as
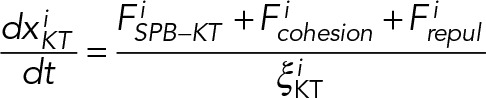 (5) (5)
|
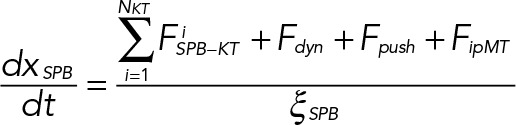 (6) (6)
|
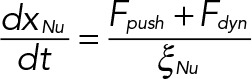 (7) (7)
|
Here the system of equations (Eqs. 5, 6, and 7) is derived in accordance with the well-known Stokes law, v = F/ξ; v, F, and ξ being the velocity, force, and viscous drag of a moving particle, respectively. The viscous drag obeys the formula ξ = 6πηr, where η is the coefficient of viscosity of the medium and r is the effective radius of the particle. Here ξKT, ξSPB, and ξNu correspond to the effective drag on a KT, SPB, and nucleus, respectively. In our model, the medium in which the KTs, SPB, and the nucleus move are the nucleoplasm, NE, and cytoplasm of the cell, respectively. The superscript i in Eq. 1 stands for the ith KT and all the “x”s in Eqs. 5, 6, and 7 are the instantaneous coordinates of the objects considered here. After SPB duplication, another set of similar equations of motion for sister KTs and daughter SPB are incorporated. The constrained motion of the SPBs along the NE is achieved using a tangential coordinate system. The constraint is relaxed once the SPBs reach the diametrically opposite ends of the nucleus. At each time step, all the forces are calculated using Eqs. 1, 2, 3, and 4, and then Eqs. 5, 6, and 7 are solved numerically to update the positions of the KTs, SPBs, and nucleus, respectively. We explore a range of values for the model parameters (Table 1) to evaluate the model predictions.
Construction of fluorescently tagged strains
The MTOC markers, Tub4 in C. albicans and Spc98 in C. neoformans, were C-terminally tagged with green fluorescent protein (GFP) to visualize the dynamics of MTOC/SPB in live cells. In C. albicans, the 3′ part of the TUB4 gene (Orf 19.1238) was amplified from the genome and cloned in a plasmid carrying the GFP-URA3, as a SacII-SpeI fragment. The plasmid was digested using PacI and transformed into C. albicans, SN148, to generate the Tub4-GFP–expressing strain. The resulting strain was used to visualize the MTOC with GFP and nuclear mass by 4′,6-diamidino-2-phenylindole (DAPI) staining during the imaging. For C. neoformans, histone H4 (ORF number CNAG_01648) was tagged with mCherry, and Spc98 (ORF number CNAG_01566) was tagged with GFP, using the overlap PCR strategy described earlier (Kozubowski, Yadav, et al., 2013). For this purpose, 1 kb each of the 3′ part of the gene and 3′ untranslated region was amplified from the genome. A GFP-NAT (nourseothricin) or mCherry-NEO (neomycin) fragment (∼3 kb) was amplified from pCN19 or pLK25 plasmids, respectively, and all three fragments were fused by overlap PCR, generating the cassettes. First, the Spc98-GFP-NAT cassette was transformed to get the Spc98-GFP strain, which was then transformed with H4-mCherry cassette to obtain a double-tagged strain. Similarly, the GFP-tubulin strain (Kozubowski, Yadav, et al., 2013) was transformed with H4-mCherry cassette to obtain the strain. The list of strains used is given in Supplemental Table S1.
Microscopy and estimation of cMT number
The dynamics of fluorescently tagged proteins within cells across various cell cycle stages were captured using a Carl Zeiss confocal laser-scanning microscope LSM 510 META (Carl Zeiss, Jena, Germany). The images were then processed using the LSM 5 Image Examiner software (Carl Zeiss) and/or Adobe Photoshop (Adobe Systems, San Jose, CA).
The number of cMTs per cell was determined by the method described previously (Kosco et al., 2001; Straube et al., 2003). Briefly, the GFP-tagged Tub1 strain of C. albicans (YJB12856) or C. neoformans (CNVY109) was grown till log phase, harvested, and mounted on an 2% agarose pad containing synthetic complete media (2% dextrose, 0.67% YNB w/o amino acids, 0.2% amino acid mix, and 100 mg/l of uridine or uracil for C. albicans or C. neoformans, respectively). GFP-tagged tubulin images of C. albicans and C. neoformans cells were captured with identical settings using a Carl Zeiss LSM 510 META confocal microscope. Images were three-dimensionally rendered using ImageJ (National Institutes of Health, Bethesda, MD). The cMTs were tracked manually using three-dimensionally rendered images across all planes. Bright clustered signals of Tub1-GFP, which represented MTOCs, were excluded from counting. Subsequent processing was performed using ImageJ and Adobe Photoshop. Cell number versus cMTs/cell was plotted using Prism (GraphPad Software, La Jolla, CA), with the calculated mean drawn for both C. albicans and C. neoformans.
MT depolymerization experiments
We performed MT depolymerization experiments using nocodazole (Sigma-Aldrich, St. Louis, MO) and MBC (Sigma-Aldrich), MT-depolymerizing drugs, to disrupt either MTs or ipMTs, respectively. Both C. albicans (LSK111) and C. neoformans (CNVY197) GFP-tagged MTOC strains were grown overnight. The overnight culture was transferred to fresh media with an initial OD600 of 0.2. The culture was grown for 3 h to get the cells in log phase (OD600 = 0.5–0.6). The cells were then treated with nocodazole (100 ng/ml for C. neoformans and 20 μg/ml for C. albicans) or MBC (1 μg/ml for C. neoformans) for 4 h. An aliquot of cells were treated with only dimethyl sulfoxide as a control. The cells were harvested after 4 h and washed with 1 ml of distilled water. Finally, cells were suspended in water, and images were captured using a microscope (DeltaVision, GE Healthcare Life Sciences) equipped with a CoolSnap HQ2 CCD. The images were then processed using ImageJ and Adobe Photoshop.
Supplementary Material
Acknowledgments
We acknowledge J. Berman for kindly providing the Tub1-GFP–expressing C. albicans strain. We are also grateful to S. Gross for interesting discussions and suggestions. We thank B. Suma for the confocal microscopy facility, Jawaharlal Nehru Centre for Advanced Scientific Research (JNCASR). Sabyasachi S., V.Y., Shreyas S., and L.S. thank the Council of Scientific and Industrial Research (CSIR), Government of India, for their fellowships. R.P. thanks the Department of Science and Technology, Government of India, for financial support (grant no. SR/S2/CMP-0107/2010). This project was partially funded by intramural funding from JNCASR to K.S.
Glossary
Abbreviations used:
- cMT
cytoplasmic microtubule
- DAPI
4′,6-diamidino-2-phenylindole
- GFP
green fluorescent protein
- ipMT
interpolar microtubule
- kMT
kinetochore microtubule
- KT
kinetochore
- MAP
microtubule-associated protein
- MBC
methyl benzimidazole carbamate
- MT
microtubule
- MTOC
microtubule organizing center
- NE
nuclear envelope
- SPB
spindle pole body
- SPOC
spindle positioning checkpoint.
Footnotes
This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E15-04-0236) on August 26, 2015.
REFERENCES
Boldface names denote co–first authors.
- Adames NR, Cooper JA. Microtubule interactions with the cell cortex causing nuclear movements in Saccharomyces cerevisiae. J Cell Biol. 2000;149:863–874. doi: 10.1083/jcb.149.4.863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akera T, Sato M, Yamamoto M. Interpolar microtubules are dispensable in fission yeast meiosis II. Nat Commun. 2012;3:695. doi: 10.1038/ncomms1725. [DOI] [PubMed] [Google Scholar]
- Anderson M, Haase J, Yeh E, Bloom K. Function and assembly of DNA looping, clustering, and microtubule attachment complexes within a eukaryotic kinetochore. Mol Biol Cell. 2009;20:4131–4139. doi: 10.1091/mbc.E09-05-0359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balasubramanian MK, McCollum D, Surana U. Tying the knot: linking cytokinesis to the nuclear cycle. J Cell Sci. 2000;113:1503–1513. doi: 10.1242/jcs.113.9.1503. [DOI] [PubMed] [Google Scholar]
- Baumgartner S, Tolic IM. Astral microtubule pivoting promotes their search for cortical anchor sites during mitosis in budding yeast. PloS One. 2014;9:e93781. doi: 10.1371/journal.pone.0093781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beach DL, Thibodeaux J, Maddox P, Yeh E, Bloom K. The role of the proteins Kar9 and Myo2 in orienting the mitotic spindle of budding yeast. Curr Biol. 2000;10:1497–1506. doi: 10.1016/s0960-9822(00)00837-x. [DOI] [PubMed] [Google Scholar]
- Best HA, Matthews JH, Heathcott RW, Hanna R, Leahy DC, Coorey NV, Bellows DS, Atkinson PH, Miller JH. Laulimalide and peloruside A inhibit mitosis of Saccharomyces cerevisiae by preventing microtubule depolymerisation-dependent steps in chromosome separation and nuclear positioning. Mol Biosyst. 2013;9:2842–2852. doi: 10.1039/c3mb70211a. [DOI] [PubMed] [Google Scholar]
- Carminati JL, Stearns T. Microtubules orient the mitotic spindle in yeast through dynein-dependent interactions with the cell cortex. J Cell Biol. 1997;138:629–641. doi: 10.1083/jcb.138.3.629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Castillon GA, Adames NR, Rosello CH, Seidel HS, Longtine MS, Cooper JA, Heil-Chapdelaine RA. Septins have a dual role in controlling mitotic exit in budding yeast. Curr Biol. 2003;13:654–658. doi: 10.1016/s0960-9822(03)00247-1. [DOI] [PubMed] [Google Scholar]
- Cepeda-Garcia C, Delgehyr N, Juanes Ortiz MA, ten Hoopen R, Zhiteneva A, Segal M. Actin-mediated delivery of astral microtubules instructs Kar9p asymmetric loading to the bud-ward spindle pole. Mol Biol Cell. 2010;21:2685–2695. doi: 10.1091/mbc.E10-03-0197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Civelekoglu-Scholey G, Sharp DJ, Mogilner A, Scholey JM. Model of chromosome motility in Drosophila embryos: adaptation of a general mechanism for rapid mitosis. Biophys J. 2006;90:3966–3982. doi: 10.1529/biophysj.105.078691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cuschieri L, Miller R, Vogel J. Gamma-tubulin is required for proper recruitment and assembly of Kar9-Bim1 complexes in budding yeast. Mol Biol Cell. 2006;17:4420–4434. doi: 10.1091/mbc.E06-03-0245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dogterom M, Yurke B. Measurement of the force-velocity relation for growing microtubules. Science. 1997;278:856–860. doi: 10.1126/science.278.5339.856. [DOI] [PubMed] [Google Scholar]
- Fink G, Schuchardt I, Colombelli J, Stelzer E, Steinberg G. Dynein-mediated pulling forces drive rapid mitotic spindle elongation in Ustilago maydis. EMBO J. 2006;25:4897–4908. doi: 10.1038/sj.emboj.7601354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finley KR, Berman J. Microtubules in Candida albicans hyphae drive nuclear dynamics and connect cell cycle progression to morphogenesis. Eukaryot Cell. 2005;4:1697–1711. doi: 10.1128/EC.4.10.1697-1711.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finley KR, Bouchonville KJ, Quick A, Berman J. Dynein-dependent nuclear dynamics affect morphogenesis in Candida albicans by means of the Bub2p spindle checkpoint. J Cell Sci. 2008;121:466–476. doi: 10.1242/jcs.015172. [DOI] [PubMed] [Google Scholar]
- Foethke D, Makushok T, Brunner D, Nedelec F. Force- and length-dependent catastrophe activities explain interphase microtubule organization in fission yeast. Mol Systems Biol. 2009;5:241. doi: 10.1038/msb.2008.76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraschini R, Venturetti M, Chiroli E, Piatti S. The spindle position checkpoint: how to deal with spindle misalignment during asymmetric cell division in budding yeast. Biochem Soc Trans. 2008;36:416–420. doi: 10.1042/BST0360416. [DOI] [PubMed] [Google Scholar]
- Gandhi SR, Gierlinski M, Mino A, Tanaka K, Kitamura E, Clayton L, Tanaka TU. Kinetochore-dependent microtubule rescue ensures their efficient and sustained interactions in early mitosis. Dev Cell. 2011;21:920–933. doi: 10.1016/j.devcel.2011.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner MK, Haase J, Mythreye K, Molk JN, Anderson M, Joglekar AP, O’Toole ET, Winey M, Salmon ED, Odde DJ, Bloom K. The microtubule-based motor Kar3 and plus end-binding protein Bim1 provide structural support for the anaphase spindle. J Cell Biol. 2008;180:91–100. doi: 10.1083/jcb.200710164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gladfelter A, Berman J. Dancing genomes: fungal nuclear positioning. Nat Rev Microbiol. 2009;7:875–886. doi: 10.1038/nrmicro2249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guertin DA, Trautmann S, McCollum D. Cytokinesis in eukaryotes. Microbiol Mol Biol Rev. 2002;66:155–178. doi: 10.1128/MMBR.66.2.155-178.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haase J, Mishra PK, Stephens A, Haggerty R, Quammen C, Taylor RM, II, Yeh E, Basrai MA, Bloom K. A 3D map of the yeast kinetochore reveals the presence of core and accessory centromere-specific histone. Curr Biol. 2013;23:1939–1944. doi: 10.1016/j.cub.2013.07.083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heath IB. Variant mitoses in lower eukaryotes: indicators of the evolution of mitosis. Int Rev Cytol. 1980;64:1–80. doi: 10.1016/s0074-7696(08)60235-1. [DOI] [PubMed] [Google Scholar]
- Horvitz HR, Herskowitz I. Mechanisms of asymmetric cell division: two Bs or not two Bs, that is the question. Cell. 1992;68:237–255. doi: 10.1016/0092-8674(92)90468-r. [DOI] [PubMed] [Google Scholar]
- Huisman SM, Bales OA, Bertrand M, Smeets MF, Reed SI, Segal M. Differential contribution of Bud6p and Kar9p to microtubule capture and spindle orientation in S. cerevisiae. J Cell Biol. 2004;167:231–244. doi: 10.1083/jcb.200407167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hwang E, Kusch J, Barral Y, Huffaker TC. Spindle orientation in Saccharomyces cerevisiae depends on the transport of microtubule ends along polarized actin cables. J Cell Biol. 2003;161:483–488. doi: 10.1083/jcb.200302030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janson ME, de Dood ME, Dogterom M. Dynamic instability of microtubules is regulated by force. J Cell Biol. 2003;161:1029–1034. doi: 10.1083/jcb.200301147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaspersen SL, Winey M. The budding yeast spindle pole body: structure, duplication, and function. Annu Rev Cell Dev Biol. 2004;20:1–28. doi: 10.1146/annurev.cellbio.20.022003.114106. [DOI] [PubMed] [Google Scholar]
- Jin QW, Fuchs J, Loidl J. Centromere clustering is a major determinant of yeast interphase nuclear organization. J Cell Sci. 2000;113:1903–1912. doi: 10.1242/jcs.113.11.1903. [DOI] [PubMed] [Google Scholar]
- Joglekar AP, Hunt AJ. A simple, mechanistic model for directional instability during mitotic chromosome movements. Biophys J. 2002;83:42–58. doi: 10.1016/S0006-3495(02)75148-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kahana JA, Schnapp BJ, Silver PA. Kinetics of spindle pole body separation in budding yeast. Proc Natl Acad Sci USA. 1995;92:9707–9711. doi: 10.1073/pnas.92.21.9707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kapoor TM, Mitchison TJ. Eg5 is static in bipolar spindles relative to tubulin: evidence for a static spindle matrix. J Cell Biol. 2001;154:1125–1133. doi: 10.1083/jcb.200106011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knoblich JA. Mechanisms of asymmetric stem cell division. Cell. 2008;132:583–597. doi: 10.1016/j.cell.2008.02.007. [DOI] [PubMed] [Google Scholar]
- Kosco KA, Pearson CG, Maddox PS, Wang PJ, Adams IR, Salmon ED, Bloom K, Huffaker TC. Control of microtubule dynamics by Stu2p is essential for spindle orientation and metaphase chromosome alignment in yeast. Mol Biol Cell. 2001;12:2870–2880. doi: 10.1091/mbc.12.9.2870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kozubowski L, Yadav V, Chatterjee G, Sridhar S, Yamaguchi M, Kawamoto S, Bose I, Heitman J, Sanyal K. Ordered kinetochore assembly in the human-pathogenic basidiomycetous yeast Cryptococcus neoformans. mBio. 2013;4:e00614–00613. doi: 10.1128/mBio.00614-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kusch J, Meyer A, Snyder MP, Barral Y. Microtubule capture by the cleavage apparatus is required for proper spindle positioning in yeast. Genes Dev. 2002;16:1627–1639. doi: 10.1101/gad.222602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laan L, Pavin N, Husson J, Romet-Lemonne G, van Duijn M, Lopez MP, Vale RD, Julicher F, Reck-Peterson SL, Dogterom M. Cortical dynein controls microtubule dynamics to generate pulling forces that position microtubule asters. Cell. 2012;148:502–514. doi: 10.1016/j.cell.2012.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee IJ, Wang N, Hu W, Schott K, Bahler J, Giddings TH, Jr., Pringle JR, Du LL, Wu JQ. Regulation of spindle pole body assembly and cytokinesis by the centrin-binding protein Sfi1 in fission yeast. Mol Biol Cell. 2014;25:2735–2749. doi: 10.1091/mbc.E13-11-0699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee L, Tirnauer JS, Li J, Schuyler SC, Liu JY, Pellman D. Positioning of the mitotic spindle by a cortical-microtubule capture mechanism. Science. 2000;287:2260–2262. doi: 10.1126/science.287.5461.2260. [DOI] [PubMed] [Google Scholar]
- Liakopoulos D, Kusch J, Grava S, Vogel J, Barral Y. Asymmetric loading of Kar9 onto spindle poles and microtubules ensures proper spindle alignment. Cell. 2003;112:561–574. doi: 10.1016/s0092-8674(03)00119-3. [DOI] [PubMed] [Google Scholar]
- Mallik R, Gross SP. Molecular motors: strategies to get along. Curr Biol. 2004;14:R971–R982. doi: 10.1016/j.cub.2004.10.046. [DOI] [PubMed] [Google Scholar]
- Marco E, Dorn JF, Hsu PH, Jaqaman K, Sorger PK, Danuser G. S. cerevisiae chromosomes biorient via gradual resolution of syntely between S phase and anaphase. Cell. 2013;154:1127–1139. doi: 10.1016/j.cell.2013.08.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markus SM, Kalutkiewicz KA, Lee W-L. Astral microtubule asymmetry provides directional cues for spindle positioning in budding yeast. Exp Cell Res. 2012;318:1400–1406. doi: 10.1016/j.yexcr.2012.04.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markus SM, Lee WL. Microtubule-dependent path to the cell cortex for cytoplasmic dynein in mitotic spindle orientation. Bioarchitecture. 2011;1:209–215. doi: 10.4161/bioa.18103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin R, Walther A, Wendland J. Deletion of the dynein heavy-chain gene DYN1 leads to aberrant nuclear positioning and defective hyphal development in Candida albicans. Eukaryot Cell. 2004;3:1574–1588. doi: 10.1128/EC.3.6.1574-1588.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McIntosh JR, Grishchuk EL, Morphew MK, Efremov AK, Zhudenkov K, Volkov VA, Cheeseman IM, Desai A, Mastronarde DN, Ataullakhanov FI. Fibrils connect microtubule tips with kinetochores: a mechanism to couple tubulin dynamics to chromosome motion. Cell. 2008;135:322–333. doi: 10.1016/j.cell.2008.08.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merlini L, Piatti S. The mother-bud neck as a signaling platform for the coordination between spindle position and cytokinesis in budding yeast. Biol Chem. 2011;392:805–812. doi: 10.1515/BC.2011.090. [DOI] [PubMed] [Google Scholar]
- Miller RK, Heller KK, Frisen L, Wallack DL, Loayza D, Gammie AE, Rose MD. The kinesin-related proteins, Kip2p and Kip3p, function differently in nuclear migration in yeast. Mol Biol Cell. 1998;9:2051–2068. doi: 10.1091/mbc.9.8.2051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller RK, Rose MD. Kar9p is a novel cortical protein required for cytoplasmic microtubule orientation in yeast. J Cell Biol. 1998;140:377–390. doi: 10.1083/jcb.140.2.377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchison T, Kirschner M. Dynamic instability of microtubule growth. Nature. 1984;312:237–242. doi: 10.1038/312237a0. [DOI] [PubMed] [Google Scholar]
- Moore JK, Magidson V, Khodjakov A, Cooper JA. The spindle position checkpoint requires positional feedback from cytoplasmic microtubules. Curr Biol. 2009;19:2026–2030. doi: 10.1016/j.cub.2009.10.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller MJ, Klumpp S, Lipowsky R. Tug-of-war as a cooperative mechanism for bidirectional cargo transport by molecular motors. Proc Natl Acad Sci USA. 2008;105:4609–4614. doi: 10.1073/pnas.0706825105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neumuller RA, Knoblich JA. Dividing cellular asymmetry: asymmetric cell division and its implications for stem cells and cancer. Genes Dev. 2009;23:2675–2699. doi: 10.1101/gad.1850809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piatti S, Venturetti M, Chiroli E, Fraschini R. The spindle position checkpoint in budding yeast: the motherly care of MEN. Cell Div. 2006;1:2. doi: 10.1186/1747-1028-1-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Powers AF, Franck AD, Gestaut DR, Cooper J, Gracyzk B, Wei RR, Wordeman L, Davis TN, Asbury CL. The Ndc80 kinetochore complex forms load-bearing attachments to dynamic microtubule tips via biased diffusion. Cell. 2009;136:865–875. doi: 10.1016/j.cell.2008.12.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pruyne D, Bretscher A. Polarization of cell growth in yeast. I. Establishment and maintenance of polarity states. J Cell Sci. 2000a;113:365–375. doi: 10.1242/jcs.113.3.365. [DOI] [PubMed] [Google Scholar]
- Pruyne D, Bretscher A. Polarization of cell growth in yeast. II. The role of the cortical actin cytoskeleton. J Cell Sci. 2000b;113:571–585. doi: 10.1242/jcs.113.4.571. [DOI] [PubMed] [Google Scholar]
- Rodal AA, Kozubowski L, Goode BL, Drubin DG, Hartwig JH. Actin and septin ultrastructures at the budding yeast cell cortex. Mol Biol Cell. 2005;16:372–384. doi: 10.1091/mbc.E04-08-0734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sau S, Sutradhar S, Paul R, Sinha P. Budding yeast kinetochore proteins, Chl4 and Ctf19, are required to maintain SPB-centromere proximity during G1 and late anaphase. PloS One. 2014;9:e101294. doi: 10.1371/journal.pone.0101294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Segal M, Bloom K. Control of spindle polarity and orientation in Saccharomyces cerevisiae. Trends Cell Biol. 2001;11:160–166. doi: 10.1016/s0962-8924(01)01954-7. [DOI] [PubMed] [Google Scholar]
- Seybold C, Schiebel E. Spindle pole bodies. Curr Biol. 2013;23:R858–R860. doi: 10.1016/j.cub.2013.07.024. [DOI] [PubMed] [Google Scholar]
- Soppina V, Rai AK, Ramaiya AJ, Barak P, Mallik R. Tug-of-war between dissimilar teams of microtubule motors regulates transport and fission of endosomes. Proc Natl Acad Sci USA. 2009;106:19381–19386. doi: 10.1073/pnas.0906524106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Straube A, Brill M, Oakley BR, Horio T, Steinberg G. Microtubule organization requires cell cycle-dependent nucleation at dispersed cytoplasmic sites: polar and perinuclear microtubule organizing centers in the plant pathogen Ustilago maydis. Mol Biol Cell. 2003;14:642–657. doi: 10.1091/mbc.E02-08-0513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Straube A, Weber I, Steinberg G. A novel mechanism of nuclear envelope break-down in a fungus: nuclear migration strips off the envelope. EMBO J. 2005;24:1674–1685. doi: 10.1038/sj.emboj.7600644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanaka K, Kitamura E, Tanaka TU. Live-cell analysis of kinetochore-microtubule interaction in budding yeast. Methods. 2010;51:206–213. doi: 10.1016/j.ymeth.2010.01.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanaka K, Tanaka TU. Live cell imaging of kinetochore capture by microtubules in budding yeast. Methods Mol Biol. 2009;545:233–242. doi: 10.1007/978-1-60327-993-2_14. [DOI] [PubMed] [Google Scholar]
- Tanaka TU, Stark MJ, Tanaka K. Kinetochore capture and bi-orientation on the mitotic spindle. Nat Rev Mol Cell Biol. 2005;6:929–942. doi: 10.1038/nrm1764. [DOI] [PubMed] [Google Scholar]
- Ten Hoopen R, Cepeda-Garcia C, Fernandez-Arruti R, Juanes MA, Delgehyr N, Segal M. Mechanism for astral microtubule capture by cortical Bud6p priming spindle polarity in S. cerevisiae. Curr Biol. 2012;22:1075–1083. doi: 10.1016/j.cub.2012.04.059. [DOI] [PubMed] [Google Scholar]
- Varga V, Helenius J, Tanaka K, Hyman AA, Tanaka TU, Howard J. Yeast kinesin-8 depolymerizes microtubules in a length-dependent manner. Nat Cell Biol. 2006;8:957–962. doi: 10.1038/ncb1462. [DOI] [PubMed] [Google Scholar]
- Varga V, Leduc C, Bormuth V, Diez S, Howard J. Kinesin-8 motors act cooperatively to mediate length-dependent microtubule depolymerization. Cell. 2009;138:1174–1183. doi: 10.1016/j.cell.2009.07.032. [DOI] [PubMed] [Google Scholar]
- Varoquaux N, Liachko I, Ay F, Burton JN, Shendure J, Dunham MJ, Vert JP, Noble WS. Accurate identification of centromere locations in yeast genomes using Hi-C. Nucleic Acids Res. 2015;43:5331–5339. doi: 10.1093/nar/gkv424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H, Oliferenko S, Balasubramanian MK. Cytokinesis: relative alignment of the cell division apparatus and the mitotic spindle. Curr Opin Cell Biol. 2003;15:82–87. doi: 10.1016/s0955-0674(02)00006-6. [DOI] [PubMed] [Google Scholar]
- Wei RR, Al-Bassam J, Harrison SC. The Ndc80/HEC1 complex is a contact point for kinetochore-microtubule attachment. Nat Struct Mol Biol. 2007;14:54–59. doi: 10.1038/nsmb1186. [DOI] [PubMed] [Google Scholar]
- Westermann S, Drubin DG, Barnes G. Structures and functions of yeast kinetochore complexes. Annu Rev Biochem. 2007;76:563–591. doi: 10.1146/annurev.biochem.76.052705.160607. [DOI] [PubMed] [Google Scholar]
- Xiang X. Nuclear positioning: dynein needed for microtubule shrinkage-coupled movement. Curr Biol. 2012;22:R496–R499. doi: 10.1016/j.cub.2012.04.044. [DOI] [PubMed] [Google Scholar]
- Yamaguchi M, Biswas SK, Ohkusu M, Takeo K. Dynamics of the spindle pole body of the pathogenic yeast Cryptococcus neoformans examined by freeze-substitution electron microscopy. FEMS Microbiol Lett. 2009;296:257–265. doi: 10.1111/j.1574-6968.2009.01643.x. [DOI] [PubMed] [Google Scholar]
- Yin H, Pruyne D, Huffaker TC, Bretscher A. Myosin V orientates the mitotic spindle in yeast. Nature. 2000;406:1013–1015. doi: 10.1038/35023024. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.