Local spectral anisotropy is a valid cue for figure-ground organization in natural scenes

Abstract

An important step in the process of understanding visual scenes is its organization in different perceptual objects which requires figure-ground segregation. The determination which side of an occlusion boundary is figure (closer to the observer) and which is ground (further away from the observer) is made through a combination of global cues, like convexity, and local cues, like T-junctions. We here focus on a novel set of local cues in the intensity patterns along occlusion boundaries which we show to differ between figure and ground. Image patches are extracted from natural scenes from two standard image sets along the boundaries of objects and spectral analysis is performed separately on figure and ground. On the figure side, oriented spectral power orthogonal to the occlusion boundary significantly exceeds that parallel to the boundary. This “spectral anisotropy” is present only for higher spatial frequencies, and absent on the ground side. The difference in spectral anisotropy between the two sides of an occlusion border predicts which is the figure and which the background with an accuracy exceeding 60% per patch. Spectral anisotropy of close-by locations along the boundary co-varies but is largely independent over larger distances which allows to combine results from different image regions. Given the low cost of this strictly local computation, we propose that spectral anisotropy along occlusion boundaries is a valuable cue for figure-ground segregation. A data base of images and extracted patches labeled for figure and ground is made freely available.

1. Introduction

The primary task of vision is to represent objects and their relationships in three-dimensional environment. Since the light from objects in three-dimensional space is projected onto the two-dimensional retina (or retinae), this is an inherently ill-posed problem. Biology and, to a lesser extent, computer vision has developed methods to deal with this difficulty heuristically. Even in complex scenes, humans and other visually oriented organisms are usually capable of gaining a good understanding of their surroundings from their visual input. Contributing to the elucidation of the mechanisms underlying this capability is the aim of this study.

Most visual objects occlude each other if they are located along the same line of sight. If the occlusion of one object by another is partial (which is the only interesting case), the question then becomes which of them is closer to the observer. The occluder is called the figure and the occluded is called ground or background. Determination of this relationship is usually referred to as figure-ground (FG) segregation, or solving the FG problem. The term is defined sometimes with a different (though related) meaning, e.g. in the context of graphics or arts, but we use it in this purely geometrical sense.

Given a scene containing objects that partially occlude each other, the task is thus to determine for each occlusion boundary (OB), which of its two sides is part of the figure and which is part of the background. The task can be solved using a multitude of cues. If two stereoscopically related images of the scene are available and the image has appropriate internal structure (a suitable texture on both the occluding and the occluded object), disparity (the distance between corresponding image elements in the two projections) can be used to determine the absolute distances of both objects from the observer. If either of these conditions is not met, or to complement a result obtained from disparity measurements, figure ground segregation needs to rely on a variety of monocular cues. These can be roughly subdivided into global and local cues, distinguished by the distance from the boundary at which information is being collected to make the FG decision.

Beginning nearly a century ago, Gestalt psychologists [2–4] established a number of “principles” that determine FG relationships. Much interest has been devoted to global cues. Some global cues of FG organization are symmetry [5], surroundedness [6], and size [7] of regions. Remarkably, in many cases FG organization can be determined from very schematic, simplified visual “scenes” with nearly exclusively global cues. Even more remarkably, von der Heydt and his colleagues [1, 8, 9] discovered that the activity of individual cells in primate extrastriate cortex represents the border-ownership relationships that likely underlie FG organization. Neuronal recordings in macaque monkeys show that the majority (about two-thirds) of orientation selective cells in area V2, the second largest visual area in macaque and the largest in humans, is border ownership selective [8, 9]. The visual stimuli in these experiments were devoid of most local cues, in fact all with the exception of a small number of L and T junctions, and even these were far away from the classical receptive fields of the recorded neurons. von der Heydt and his collaborators found that neurons in early and intermediate visual areas nevertheless represented the global structure of the scene. This was the case even though the classical receptive fields of the recorded neurons only covered a very small fraction of the perceived figure and ground elements. Understanding the mechanisms underlying these neuronal responses is a field of active study [10–13].

In more complex, realistic scenes, determination of figure ground relationships is not limited to global cues; instead, important contributions are made by local cues, too. Examples of local cues are T-junctions [14], convexity [15, 16], and shading [17], including extremal edges [18, 19]. Understanding how any or all of these local cues contribute to FG segregation is important for computational performance since, different from the global cues, they can be computed from a small number of pixels of the original image which can reduce computational complexity substantially. Even if a single local cue only gives incomplete information by providing a bias for one or the other (binary) interpretation, combining several or many of these cues may “solve” the FG determination problem in a statistical sense, and may require less computational resources than the use of global cues. Complex situations most likely require the integration of both global and local cues for a hybrid solution of the problem.

In this report, we focus on a novel class of local cues, the anisotropy of spectral power along and across the OBs. We show that this measure by itself is surprisingly informative about FG relationships, with a discrimination accuracy exceeding 60% when applied to a single location on the OB. These measures are related to the already mentioned shading patterns at the edges of objects [17], including extremal edges [18, 19].

We provide a context for our work in Section 2, introduce our basic measures in Section 3, define them formally in Section 4, and apply them to a large set of natural scenes in Section 5. We conclude with a Discussion in Section 6.

2. Related Work

In this study, we investigate the spectral properties of small patches of natural images extracted along the OBs for the purpose of identifying local cues of FG organization. Spectral properties of natural images have been studied from various perspectives. Several authors [20-23] have analyzed the statistics of entire images and shown that the power of the rotationally averaged spectrum varies inversely with spatial frequency, a key property that gives rise to scale-invariance in natural images. van der Schaaf and van Hateren [24] showed that the distribution of spectral power is not isotropic but is higher for horizontal and vertical than other orientations. It was shown that rough depth estimation [25] and limited scene categorization [26] can be performed based on the Fourier energy spectrum of entire images.

For the task of establishing FG relationships that we focus on, spatial frequency as a global cue has been studied behaviorally for more than a half century. Gibson [27] claimed that regions with low spatial frequency are likely to be perceived as figure and those with higher spatial frequency as ground. Contrastingly, in the psychophysical experiments of Klymenko and Weisstein [28], it was found that a region with higher spatial frequency was perceived as figure on more occasions than regions with lower spatial frequency. Note that in these and later behavioral studies, spatial frequency was averaged (separately) over the entire figural and ground regions. These studies did not consider variations of spatial frequency as a function of the distance from the figure/ground boundary nor as a function of orientation, along or orthogonal to the boundary, which is the analysis we perform in the present study. Moreover, in most of these earlier psychophysical experiments artificial stimuli were employed rather than natural scenes.

Fowlkes et al. [7] showed that figural regions are locally smaller and more convex, and that they are often situated below the OB. In a related investigation [29], the convexity of the OB, a local FG cue, was found to increase the perceived depth difference between figure and ground. Ren et al. [30] used local shapeme models to perform FG assignment in natural images. These authors used a logistic classifier algorithm to locally assign figure/ground labels, and a Conditional Random Field based global model to enforce consistency of FG relationships at T-junctions. Their local and global models achieve 64% and 78% accuracy respectively in determining correct FG relationships. Geisler et al. [31] train neurally-inspired models for, among other tasks, FG classification. Different from their work, our approach does not use any training; instead we directly exploit the statistics of natural scenes, as will be discussed below in Sections 3 and 6. Furthermore, the description of the stimulus encoder “neurons” in [31] is in the spatial domain while we use information in the spectrum. Another difference is that only foliage data is used in the Geisler et al. study [31] while we use images of natural scenes from a large number of different scene classes. A more recent abstract also reported results on the interaction of local cues (convexity and closure) for FG segregation [32].

An interesting heuristical approach in the computer vision literature combines various image cues, both local and global, to infer 3D depth information from 2D images [33, 34]. From a set of elementary assumptions, e.g., that neighboring pixels belong to the same surface if there is no edge between them, that long straight lines belong to structures like buildings, sidewalks or windows, that the sky is on top of the image etc, Saxena et al. [34] reconstruct a 3D depth map from a single 2D image. Even though these cues are not explicitly designed for FG segregation, inferring the depth-wise arrangement of a scene necessarily leads to the determination of FG relations in many cases.

In summary, previous investigations of FG relationships in the spectral domain have focused on either the global power spectrum of the entire image, or the local power spectrum in different parts of the image. We decided to extend these approaches by taking into account the location of OBs. In our study, we compute the local spectral power in small patches selected from natural scenes that are adjacent to known OBs, with the goal of determining on which side of the boundary the figure is situated. Specifically, we study the variation of spectral power in different orientations with respect to the FG boundary, parallel and orthogonal to it. Based on our analysis, we devise a simple FG discrimination rule.

3. Spectral Anisotropy Close to Object Boundaries

The study of spectral anisotropy (SA) at occlusion boundaries is motivated by the observation of fundamental properties of the physical world. Objects tend to be convex, opaque and textured, the combination of which leads to the appearance of a feature gradient near the OB. As a consequence, there are systematic differences in the local statistics between the areas of the figure and of the ground which are adjacent to the OB. While visual patterns in the background are not affected by the occlusion, features change in a characteristic way on the figure side. Following theoretical work by Huggins et al. [17], Palmer and Ghose [18] showed that the characteristic feature gradients on the figure side (the so-called extremal edges) can be used by human observers for figure ground segregation. The components of extremal edges in natural scenes can be identified and classified using Principal Component Analysis [17, 19]. We therefore decided to exploit the predicted differences between feature gradients along the OB and orthogonal to it by characterizing them in terms of local discrete Fourier transforms and then quantifying localized spectral image statistics on the two sides of the boundary.

We select pairs of image patches of size K × K that straddle the OB at a number of locations along the OB. At a given location on the OB, a pair of patches, one located on the figure side and its counterpart on the background side is extracted, see Appendix D for the procedure. The pixels on the OB between them are not considered part of either patch. A patch is denoted by ψ_s(x,y), where the subscript s denotes the side of OB containing figure (f) or ground (g),

$$s≔\{\begin{array}{cc}f\text{if}{\psi }_s(x,y)\hfill & \text{is on the figure side}\hfill \\ g\text{if}{\psi }_s(x,y)\hfill & \text{is on the ground side}\hfill \end{array}\phantom{\}}$$ (1)

Let us define a local coordinate frame in the patch ψ_s(x,y) with x varying parallel to the OB, and y orthogonal to it. The oriented power spectrum parallel to the OB of a patch on side s is defined as,

$$E_{s\parallel }(u,y)={\mid {\Psi }_s(u,y)\mid }^2$$ (2)

where Ψ_s(u,y) is the (windowed, see next paragraph) one-dimensional Discrete Fourier Transform (DFT) of ψ_s(x,y) with respect to x (parallel to the boundary, denoted by the symbol ∥) at distance y from the boundary, and u is the spatial frequency variable corresponding to parallel orientation.

The definition of Ψ_s(u,y) in eq 2 is ${\Psi }_s(u,y)={\mathcal{F}}_x\{{\psi }_s(x,y)\times h(x,y)\}$, where ${\mathcal{F}}_x(.)$ denotes the 1-D DFT with respect to x, and $h(x,y)=0.54-0.46\cos \left(2\pi \frac{x}{K}\right)$ is the 1-D Hamming window applied to row y. Note the absence of any dependence on y in the Hamming window, it is applied to each row independently before computing the DFT to reduce boundary artifacts [35]. Results do not depend critically on the windowing function, we repeated the analysis using a Bartlett window and obtained very similar results.

The average oriented power spectrum of the patch ψ_s(x,y) parallel to the OB is obtained as

$${\overline{E}}_{s\parallel }\left(u\right)=\frac{1}{K}\sum _{y=0}^{K-1}{E}_{s\parallel }(u,y)$$ (3)

The average oriented power spectrum of a patch orthogonal to the OB, ${\overline{E}}_{s\perp }$, is computed analogously, with the one-dimensional Fourier transform now performed on the y coordinates, and the Hamming window applied correspondingly.

The total oriented spectral power (a scalar) of ψ_s(x,y) in the frequency range {u₁,..., u₂}, parallel to the OB is,

$${\left[T_{s\parallel }\right]}_{u_1}^{u_2}={\int }_{u_1}^{u_2}{\overline{E}}_{s\parallel }\left(u\right)du$$ (4)

The total oriented spectral power of the patch orthogonal to the OB, ${\left[T_{s\perp }\right]}_{v_1}^{v_2}$, is computed analogously.

The ratio of orthogonal to parallel total oriented spectral power for patch ψ_s, s ∈ {f,g} is defined as the SA,

$${\rho }_s(u_1,u_2,v_1,v_2)=\frac{{\left[T_{s\perp }\right]}_{v_1}^{v_2}}{{\left[T_{s\parallel }\right]}_{u_1}^{u_2}}$$ (5)

When ρ_s(u₁, u₂, v₁, v₂) is equal to unity, the patch is said to be spectrally isotropic, otherwise it is spectrally anisotropic.

The unoriented total spectral power T̄_s(u₁, u₂, v₁, v₂) of a patch is defined as the average of the oriented spectral powers, ${\left[T_{s\parallel }\right]}_{u_1}^{u_2}$ and ${\left[T_{s\perp }\right]}_{v_1}^{v_2}$. For example,

$${\stackrel{‒}{T}}_f(u_1,u_2,v_1,v_2)=\frac{1}{2}({\left[T_{f\parallel }\right]}_{u_1}^{u_2}+{\left[T_{f\perp }\right]}_{v_1}^{v_2})$$

is the unoriented total spectral power of the figure side.

4. Data and Methods

We use two image databases freely available on the internet, the MIT LabelMe [36] collection and the Berkeley Segmentation Data Set, BSDS300 [37], to prepare our datasets of image patches.

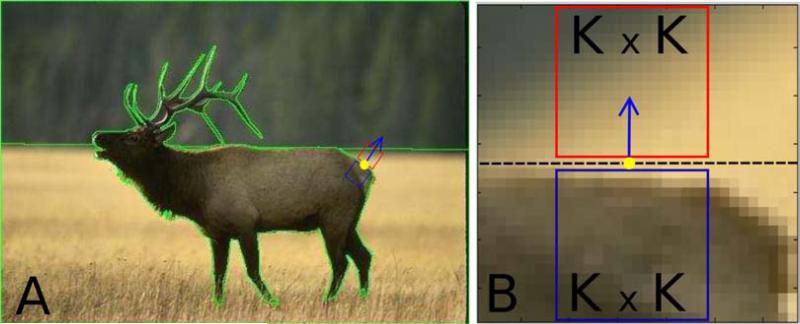
The BSDS300 database consists of 300 images, all with an image size of 481 × 321 pixels. The database also contains human-drawn contours along the object boundaries to segment objects in the scenes, with one boundary map per observer and image. Most images have multiple boundary maps. The number of segmented regions varies both across images, for the same observer, and across observers, for the same image. For each image, we chose the boundary map that had the smallest number of segmented parts (five images in the database did not have any associated boundary maps and were not used). The location along the OB (yellow dot in Figure 2A) at which K × K figure and ground patches were extracted is generated by randomly drawing (without replacement) one location (i.e., one pixel) from among all locations (pixels) in the boundary map. Patches were then rotated to a common orientation such that the orientations orthogonal and parallel to the OB in the image coincide with y- and x-axes respectively of the rotated patch as described in Appendix D. All patch rotations were done in the image plane and a bi-linear interpolation scheme [38] was used to compute pixel values at the rotated locations. We collected 5 figure patches and their background counterparts per image, a total of 1475 FG patch pairs from the BSDS300 dataset. We are interested in systematic effects along an OB but not in the influence of structural cues like L-junctions or T-junctions. Therefore, if any of the patches contained a clear T-junction or L-junction, it was replaced by another patch randomly selected from the same contour in the same image. This was the case in 113 out of the 1475 total (81 T-junctions and 32 L-junctions).

Figure 2.

Patch extraction. (A) Example image. The green lines are the human-labeled object boundaries, the yellow dot on the boundary is the randomly selected boundary location from which a pair of figure and ground patches is extracted. The blue and red boxes contain figure and ground patches respectively in their original orientation. The blue arrow points towards the background. (B) Image patches after rotation. The boundary of the object is the row of pixels in the center (dashed black line), which is considered a part of neither the figure, nor the ground. The bottom K × K blue square is the figure patch (occluding object) and the red top square is the ground patch. A slightly larger area containing figure and ground patches is shown so that context of patch on the boundary is clear. For all analyses except in Appendix A, K = 16.

The MIT LabelMe database consists of a very large number of user-contributed images with user-labeled objects but without accurate boundary maps. Our goal was to generate a set of images that is representative of a broad range of natural scenes, to avoid a systematic preselection for specific types of patches and to reduce the effect of biases such as illumination, frequently occurring foreground and background types, local curvatures, textures, color variations etc. Therefore we selected 585 images from five categories: office environment, other indoor scene (living room, kitchen etc), street, beach, and forest. Due to the heterogeneous nature of the database, the selected images varied in size from 256 × 256 to 2048 × 1500 pixels. Since no object boundary maps were provided, patch locations were selected on perceived boundaries by a human observer (the first author). Patches were then rotated to a common orientation, see Appendix D. Again, patches with T and L-junctions were avoided during the selection process. A total of 1761 figure patches and their ground counterparts were collected, with a varying number of patch pairs from each image. Numbers of images and FG patch pairs in the different categories are given in Table 1.

Table 1.

Number of images and figure-ground pairs used from the LabelMe Dataset, by image category.

Category	Number of Images	Number of patch pairs
Indoor	199	524
Beach	138	480
Office	62	204
Street	120	340
Forest	64	213
Total	585	1761

The patch extraction process is illustrated in Figure 2; for the detailed procedure see Appendix D. The blue and red boxes in Figure. 2A enclose a pair of figure and ground image patches respectively in their original orientation. The blue arrow is positioned at the OB location centered on the extracted patches, and it is oriented orthogonal to the OB pointing toward the background. The pair of rotated, bi-linearly interpolated patches, each denoted by ψ_s(x,y) are shown in Figure 2B (note pixelation). After rotation, patches are converted from RGB colorspace to 8-bit grayscale where the intensity I of the patch is obtained from the Red, Green and Blue color channels R, G and B as I = 0.2989 × R + 0.5870 × G + 0.1140 × B [39]. All analyses described in Section 3 are performed on these grayscale patches.

For all analyses throughout the paper, figure and ground patches of 16×16 pixels are used (other sizes are discussed in Appendix A), an example is shown in Figure 2B. One dimensional DFTs are computed on the figure and ground patches separately, as described in Section 3. We compare the distribution of spectral power in a patch between orthogonal and parallel orientations on a one-to-one basis (Equations 3 and 4). In the Fourier domain, this gives us 8 bins for each orientation. In Sections 5.1 and 5.2, comparison of both oriented and unoriented spectral power distributions is made between figure and ground.

We study the spectral properties of image patches in the BSDS300 and LabelMe databases separately because of the following reasons: (1) In the set derived from the LabelMe database, the images were contributed by users unknown to database providers, but the location of patches on the OB was hand-selected by a human observer (because boundary maps were unavailable), rather than randomly placed on the boundary. We want to make sure that any biases that may have been introduced by the manual selection of patch locations on the boundaries can be isolated by comparing with the BSDS300 (random selection on the boundaries) results, see Section 6 for related discussion. It should be pointed out though that at the time of patch collection (for both datasets), our goal was to identify all potential local cues of FG organization and that the human observer was unaware of the potential importance (and even existence) of any SA cues. (2) There are some major differences between the BSDS300 and LabelMe databases. While LabelMe consists of user contributed images of varying complexity and quality, ranging from shots taken by untrained observers with simple point-and-shoot cameras to images composed by professional photographers using high-performance equipment, BSDS300 images are hand-selected by database providers, have rich texture and uniformly smaller (481 × 321 pixels ≈ 0.15 megapixels) than more than half of LabelMe images (see Table B.5 for LabelMe image sizes). We want to verify SA is not affected by biases that may have been introduced at the time of image selection, see Section 6 for related discussion. (3) A wide range of image sizes available in LabelMe and a fixed image size of BSDS300 with human marked boundaries allow us to test the performance of SA as a function of a some relevant parameters. The robustness of SA as a FG cue with varying image sizes is discussed in Appendix B, while its effectiveness as a function of patch size in Appendix A.

All images and extracted patches labeled for figure and ground are available at cnslab.mb.jhu.edu.

5. Results

In the following sections, we perform a series of related analyses, using the same statistical procedure in all cases. Using a χ² goodness of fit test, we found that distributions are not normal. We therefore used Wilcoxon signed-rank tests, the analogue of paired sample student's t-tests for normal distributions, in all the following analyses, always with a significance level α = 0.05. The number of samples (FG patch pairs) is 1475 for BSDS300 and 1761 for LabelMe databases respectively. For the χ² goodness of fit test, 30 bins are used but results are not shown explicitly.

To orient the reader, we begin with a brief summary of the results. In Sections 5.1-5.3, we first check if mean pixel intensity (power in bin 1) or total unoriented power (T̄_s(1, 8, 1, 8)) of patches of the two sides can predict FG relationships. After verifying that those quantities are not useful, we find statistically significant differences in the spectral power of high frequency bins (specifically, T̄_f(3, 8, 3, 8) > T̄_g(3, 8, 3, 8)). We then investigate the origin of this difference by comparing oriented spectral power with two orientations, orthogonal and parallel to the OB. We find that in the background there is no difference between oriented spectral powers, parallel and orthogonal to the boundary (as one might expect) while on the figure side, ${\left[T_{f\perp }\right]}_3^8>{\left[T_{f\parallel }\right]}_3^8$ (which is a novel and, as we later show, useful observation). This effect is what we call SA. A more detailed explanation of the geometrical structure that likely gives rise to SA is given in Section 6.

After establishing SA as a valid cue for FG organization, we investigate in Section 5.4 how it varies as a function of the distance between patch locations along the boundary. This is important to evaluate the efficiency with which information from multiple boundary locations can be combined to make reliable FG classification decisions. Finally in Section 5.5 we train a non-linear Support Vector Machine to show how a non-linear classification rule improves FG classification accuracy based on SA. The method is robust to changes in patch and image sizes, as shown in Appendix A and Appendix B.

5.1. Basic spectral properties along the boundary

First we test whether there is a systematic intensity difference between the sides, i.e. whether the figure side is consistently brighter than the ground or vice-versa. We compare the distributions of unoriented spectral power in the first bin (corresponding to mean pixel intensity or DC level) across all patches using a Wilcoxon signed-rank test to verify whether the distribution medians are statistically different [40]. We cannot reject the null hypothesis that the two distributions are identical with similar medians (BSDS300 (T̄_f(1, 1, 1, 1) vs. T̄_g(1, 1, 1, 1)): p = 0.20; LabelMe: p = 0.66). Therefore, intensity cannot be used to determine figure ground organization. Next, we compare the distribution of total unoriented spectral power of all figure patches against those of ground patches (i.e. T̄_f(1, 8, 1, 8) vs. T̄_g(1, 8, 1, 8)). Again a Wilcoxon signed-rank test shows that the null hypothesis (medians are equal) cannot be rejected (BSDS300: p = 0.32; LabelMe: p = 0.67).

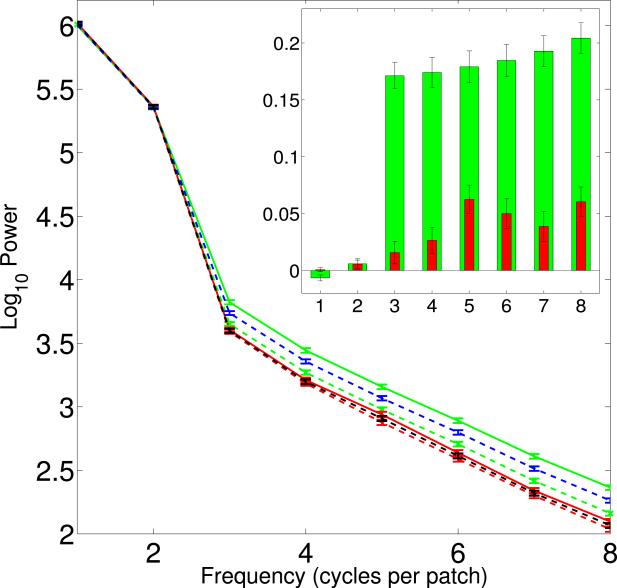
While there are thus no systematic differences in mean pixel intensity or total power on the two sides, we do observe power differences between T̄_f(3, 8, 3, 8) and T̄_g(3, 8, 3, 8). Figure 3 shows that the unoriented spectral power (dashed blue and black lines indicating figure and ground respectively) in bins {3,..., 8} on the figure side is higher than on the background side. Statistical significance tests confirm that T̄_f(3, 8, 3, 8) in figure is greater than T̄_g(3, 8, 3, 8) in ground (Wilcoxon signed-rank tests - BSDS300: p = 2.79 × 10⁻²⁴ ; LabelMe: p = 1.08 × 10⁻⁴).

Figure 3.

Average power spectra of all patches of BSDS300 data as function of spatial frequency. The unoriented spectra are represented by dashed blue (figure) and black (ground) lines. The oriented spectra in the plot are: ${\overline{E}}_{f\perp }$ (solid green line), ${\overline{E}}_{f\parallel }$ (dashed green line), ${\overline{E}}_{g\perp }$ (solid red line) and ${\overline{E}}_{g\parallel }$ (dashed red line). Inset: The difference in power orthogonal and parallel to the OB (${\log }_{10}({\stackrel{‒}{E}}_{s\perp }-{\stackrel{‒}{E}}_{s\parallel })$) as function of spatial frequency. Axes are the same as in the main figure. Green and red bars represent figure (s = f) and ground (s = g) differences respectively. Error bars are standard errors in figure and inset. Significant differences are only observed for higher frequencies (bins 3-8), and they are significantly larger for the figure than for the ground side. Results from the LabelMe database are similar, see Appendix C.

A possible explanation for the occurrence of elevated power levels in bins {3,..., 8} on the figure side is the presence of anisotropic spectral power distributions. Motivated by our and others’ observations of differences in the spatial structure on the two sides of an OB [17–19], we decided to consider oriented spectral power with respect to the OB.

5.2. Spectral Anisotropy

We quantify SA in figure and ground separately in two orthogonal orientations with respect to the OB, as detailed in Section 3. In Figure 3, we show the mean spectra of all patches in the BSDS300 dataset, for an analogous plot for LabelMe see Appendix C. The figure shows: the oriented power spectra of (1) figure orthogonal to the OB, ${\overline{E}}_{f\perp }$ (solid green line); (2) figure parallel to the OB, ${\overline{E}}_{f\parallel }$ (dashed green line); (3) ground orthogonal to the OB, ${\overline{E}}_{g\perp }$ (solid red line); (4) ground parallel to the OB, ${\overline{E}}_{g\parallel }$ (dashed red line); and also the unoriented power spectra (dashed blue and black lines representing figure and ground sides respectively). The error bars indicate standard error. We see that for bins 1-2, there are no differences between any of the oriented spectral power levels. Even at higher frequencies (bins 3-8), the mean spectra for the background in both orientations overlap with each other. However, at these higher frequencies, on the figure side, power orthogonal to the OB is higher than parallel to the boundary.

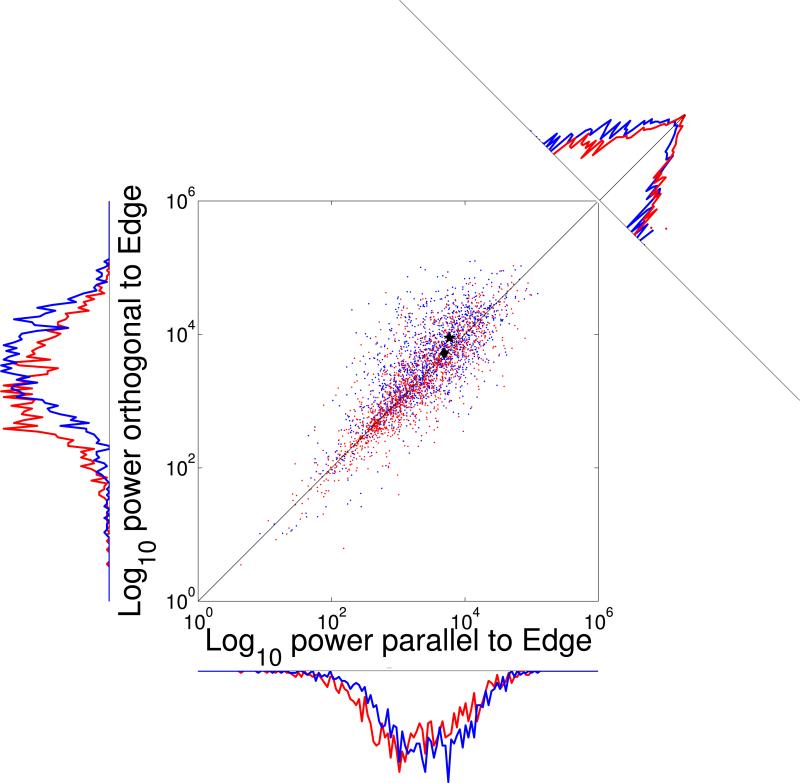
We therefore proceed to compare the oriented power on the two sides only for the high-frequency bins. The distribution of ${\left[T_{s\perp }\right]}_3^8$ vs. ${\left[T_{s\parallel }\right]}_3^8$ for all 1475 patches from the BSDS300 data set is shown in Figure 4, using blue dots for the foreground (${\left[T_{f\perp }\right]}_3^8$ against ${\left[T_{f\parallel }\right]}_3^8$) and red dots for the background (${\left[T_{g\perp }\right]}_3^8$ against ${\left[T_{g\parallel }\right]}_3^8$). The abscissa and ordinate thus represent total power (bins 3–8) parallel and orthogonal to the OB, respectively. The marginals along the two axes seem to show a shift towards higher frequencies of the figure vs. the ground both parallel and orthogonal to the edge. The origin of this shift is unclear; it could be due to the photographers focusing on the foreground rather than the background, resulting in more power in the higher spatial frequencies on the foreground than the background side. Therefore, we do not exploit this effect (which is absent in the LabelMe data, see Appendix C) for FG segregation. Instead, we observe a bias indicating ${\left[T_{f\perp }\right]}_3^8>{\left[T_{f\parallel }\right]}_3^8$ on the figure side (blue) relative to the background (red) in the marginals along the diagonal, as predicted by SA. Note that the large range required use of a logarithmic scale for the ordinate for this marginal (but not for the marginals along the axes) which graphically de-emphasizes the size of the effect.

Figure 4.

Two-dimensional distribution of spectral power in bins 3–8 orthogonal vs. parallel to the OB for all BSDS300 patches. Red, background (${\left[T_{g\perp }\right]}_3^8$ vs. ${\left[T_{g\parallel }\right]}_3^8$); blue, figure (${\left[T_{f\perp }\right]}_3^8$ vs. ${\left[T_{f\parallel }\right]}_3^8$). The black diamond, very close to the identity line, shows the mean of the background. The black asterisk, above the identity, shows the mean of the figure. The distance between the figure-side mean and the identity line is even larger for LabelMe, see Appendix C. The marginal distributions along the scatter plot axes, with linear ordinates, show that average power on the figure side exceeds that on the ground side both parallel and orthogonal to the OB. While this effect seems quite strong here, we do not exploit it for FG segregation since it is absent in the LabelMe data. The marginal distribution at the top right collapses data along the diagonal and has a logarithmic ordinate since the values of the central bins vastly surpass those of other bins. This marginal shows the presence of spectral anisotropy (blue curve above the red one left of diagonal). Again, the effect is stronger in the LabelMe data.

Next, we test if this difference is statistically significant. The comparison is made for the two sides separately. The distributions were found to be non-normal with χ² goodness-of-fit tests. A Wilcoxon signed-rank tests indicate that for the figure, the power orthogonal (${\left[T_{f\perp }\right]}_3^8$) to the OB is higher than that parallel (${\left[T_{f\parallel }\right]}_3^8$) to the figure/ground boundary (BSDS300: p = 3.03 × 10⁻³¹; LabelMe: p = 2.18 × 10⁻⁸⁵). In contrast, for the ground, oriented power levels (${\left[T_{g\parallel }\right]}_3^8$ and ${\left[T_{g\perp }\right]}_3^8$) are not significantly different (BSDS300: p = 0.72; LabelMe: p = 0.26). This indicates an anisotropic distribution of high frequency spectral power on the figure, but not the ground side. A linear regression model, with slope as the only parameter (forced to pass through the origin), was fitted to the distributions of the log₁₀-transformed power, ${\left[T_{s\parallel }\right]}_3^8$ and ${\left[T_{s\perp }\right]}_3^8$, for figure and ground separately. The model exhibits different slopes, with non-overlapping confidence intervals. The slopes significantly exceed unity on the figure side but not on the ground side. Results for both data sets are shown in Table 2.

Table 2.

Regression of log₁₀-transformed high-frequency spectral power in orthogonal and parallel orientations with slope as the only parameter. Results for both datasets show slopes close to unity in the background and greater than unity (and higher than background) in the figure, with their confidence intervals (CIs) non-overlapping. This indicates higher oriented spectral power orthogonal to the boundary than parallel to it on the figure side.

		slope(radians)	CI (low)	CI (high)	R 2
BSDS300	Figure (orthogonal vs. parallel)	1.036	1.030	1.043	0.53
	Ground (orthogonal vs. parallel)	0.998	0.993	1.004	0.71
LabelMe	Figure (orthogonal vs. parallel)	1.0722	1.065	1.079	0.53
	Ground (orthogonal vs. parallel)	1.006	0.995	1.006	0.57

5.3. Figure-ground classification based on SA

Can the observed SA be used for determining figure-ground segregation? To answer this question, we developed a FG classification test based on the ratio of oriented spectral powers, bins 3–8. Note that our method does not involve any training, instead, the test is developed from first principles, i.e. the statistics of natural scenes discussed above, see also Huggins et al. [17], Palmer and Ghose [18], and then validated on two different data sets.

Let us denote the two sides of a given patch pair by s₁ and s₂ respectively, where s₁ and s₂ can be either figure or ground. Let ρ_s1(3, 8, 3, 8) and ρ_s2(3, 8, 3, 8) be the corresponding ratios (defined in Eq 5) of the two sides. We decide whether side s₁ is figure or ground based on the following rule:

$$s_1≔\{\begin{array}{cc}\text{figure}\hfill & \text{if}{\rho }_{s_1}>{\rho }_{s_2}\hfill \\ \text{ground}\hfill & \text{if}{\rho }_{s_2}\ge {\rho }_{s_1}\hfill \end{array}\phantom{\}}$$ (6)

where we omitted the arguments of ρ_s1 and ρ_s2. The classification rule in Equation. 6 is a maximum likelihood classification rule, where a patch is classified as belonging to one of the two classes only if its likelihood of belonging to that class is maximum (see Appendix G for a detailed explanation). The test yields a classification accuracy of 62.57% for the BSDS300 and 64.51% for the LabelMe datasets respectively. This is a central result of our study. Inverting the pixel intensities on both sides gives very similar results (BSDS300: 61.15%, LabelMe: 66.21%). This again indicates that SA is purely a function of spatial frequency content of the local patch along the OB and that mean pixel intensities have no influence on the properties observed.

As an illustration of FG classification results, a sample of 8 images from the BSDS300 database is shown in Figure 5. Half of the images show a sharp background (large depth of field, DOF) and the other half a blurry background (small DOF). A blue rectangle is drawn around the patches; green and red arrows indicate correct (pointing to figure side) and incorrect (pointing to ground side) classifications, respectively, based on SA (Section 5.2 and Eq. 6). The length of an arrow is proportional to the ratio ${\rho }_{s_1}(3,8,3,8)∕{\rho }_{s_2}(3,8,3,8)$ and signifies confidence in the decision. Figure-ground classification is effective both in images with small and with large DOF.

Figure 5.

Example FG assignments for BSDS300. Blue boxes indicate figure and ground patches, green arrows correct FG assignment, red arrows incorrect assignment. Length of the arrows indicates the confidence level in our classification method. The top four images have large DOF where the entire scene is in focus. In the bottom four images a specific object is focused by the photographer leaving the rest of the scene blurred. As the arrows on the randomly selected patches show (most are green), spectral anisotropy is a useful indicator of figure vs. ground.

5.4. Combining multiple classification decisions

Can evidence about FG relations from multiple patches along an OB be combined to improve the reliability of the classification? The extent to which this is possible is determined by the degree of dependence between decisions at individual patches. Here we study the simplest case of pairwise correlations between figure/ground classification decisions at two locations that are r pixels distant.

The analysis is done for the BSDS300 database only. We used the same 1475 figure/ground patch pairs from Section 5.1 which we call Dataset 1. In an image, I^j(x,y), j ∈ {1,..., 300}, at location ${\mathbf{u}}_i^j=(x_i^j,y_i^j)$ (yellow dot in Figure 6) on an OB in Dataset 1, we draw a circle (dashed black) whose radius r is a random number uniformly distributed between 1 and 50. The circle intersects the boundary in, at least, two points. One of these is selected randomly (with equal probability) and the figure/ground patch pair at this location ${\mathbf{u}}_k^j=(x_k^j,y_k^j)$ (red dot in Figure 6) is an entry in a new set of 1475 image patch pairs that we call Dataset¹ 2.

Figure 6.

Extracting Dataset 2 patches. The yellow dot on the boundary (green line) is the center of one patch pair (red and blue squares) from Dataset 1. A circle of radius r (black dashed line) is drawn around it, and one of its intersections with the contour (red dot) is selected as the center of a new patch pair which is entered into Dataset 2.

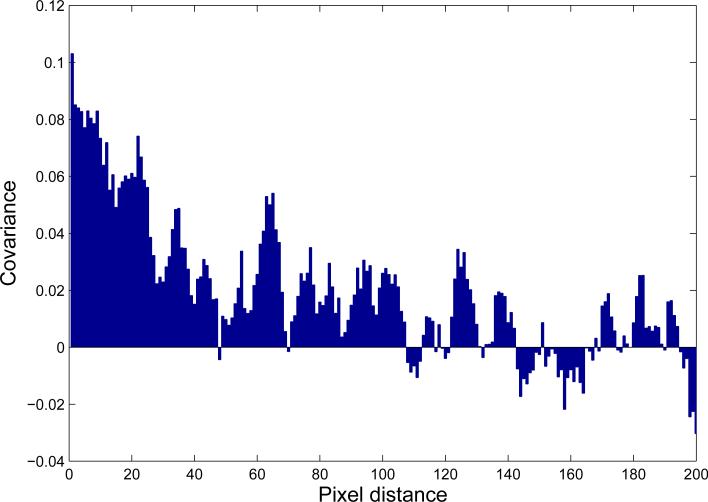
Let $d_i^j$ be a figure/ground classification decision associated with a pair of figure/ground patches at ${\mathbf{u}}_i^j$, where $d_i^j=0$ stands for a correct and $d_i^j=1$ for an incorrect decision. The expectation value $E\left[d_i^j\right]$ of $d_i^j$ is the probability of classification error, $P_e\left(d_i^j\right)$. For the BSDS300 data set, the probability of correct classification is 0.625, therefore the probability of error $P_e\left(d_i^j\right)$ is 0.375. If $d_i^j$ and $d_k^j$ are independent, the joint probability of error is $P_e(d_i^j,d_k^j)=P_e\left(d_i^j\right)P_e\left(d_k^j\right)$. But, if they are not independent, by the definition of covariance, $P_e(d_i^j,d_k^j)=E\left[d_i^j\right]E\left[d_k^j\right]+{\sigma }_e(d_i^j,d_k^j)$, where ${\sigma }_e(d_i^j,d_k^j)$ is the covariance between $d_i^j$ and $d_k^j$. We therefore determined the error covariance, ${\sigma }_e(d_i^j,d_k^j)$ between all possible decision pairs $(d_i^j,d_k^j)$ within each image to see at which distance r between patches the error covariance term is small enough so we can drop it.

A plot of ${\sigma }_e(d_i^j,d_k^j)$ vs. r is shown in Figure 7. The covariance is positive for small distances (as could be expected), and then falls off quite rapidly. For r ≈ 30, at which the two locations on the boundary are separated by a distance double the patch size, covariance is already quite small, about 0.02. Values remain mainly positive until r ≈ 100 which may reflect the average size of objects in the images. Beyond this distance, correlations fluctuate around zero.

Figure 7.

Covariance of classification decision, ${\sigma }_e(d_i^j,d_k^j)$ vs. pixel distance r along the OB. The covariance is high and positive for small distance, less than 5 pixels. Covariance drops off as r increases. For distances up to about 100 pixels, ${\sigma }_e(d_i^j,d_k^j)$ is mainly positive after which it is small and fluctuates randomly. A smoothing running average filter of width 7 is used.

In conclusion, covariance analysis shows that decisions are only weakly correlated at distances exceeding about twice that of a patch (r ≳ 2K). Such patches can be regarded as independent, and the FG decisions from those locations can be combined to improve classification reliability.

5.5. Classification By Support Vector Machine

In Section 5.3, we used a linear discrimination rule based on the SA property, namely the difference in ratios of spectral power of figure and ground. We arrived at this rule based on statistical significance tests and regression analysis. From the logarithmic plots of total power in high frequency bins (Fig 4), we see that there is overlap in the distribution of these ratios. We therefore hypothesized that in a higher dimensional space, the four spectral power levels may be well separated, hence amenable to higher classification accuracy. Therefore we go from the ratios of spectral power levels to a four-dimensional space (the four spectral power levels) and train a Support Vector Machine (SVM) model in the 4D dimensional space. We use a non-linear classification rule by training the model with radial basis function kernels. The analysis was carried out for LabelMe and BSDS300 databases separately. The patch databases (1761 patch pairs for LabelMe, 1475 for BSDS300) were divided into training and test sets. Two thirds of the samples were used for training and the remaining one third for testing, and the partition into these subsets was random. The training patch pairs are further divided into correct (positive) and incorrect (negative) classification examples (50:50 ratio). The SVM model was trained with ten-fold cross validation. Full details about training and testing can be found in Ramenahalli et al. [41]. From the results (Table 3), we see that use of the SVM improves classification accuracy for both datasets, reaching nearly 70% for BSDS300.

Table 3.

SVM results. For both databases (column 1), we show the number of image patch pairs in the test set (column. 2) and the percentage of correct FG assignments (column 3).

Database	Number of test patch pairs	Accuracy
LabelMe	587	67.12
BSDS300	491	69.25

6. Discussion

Our results show that spatial frequency power perpendicular to the object boundary exceeds that parallel to the object boundary at high spatial frequencies, and that no such difference exists on the background side. We believe that this difference is caused by the visual compression of features on the figure due to the surface curvature of convex objects, as discussed in the next paragraph. Therefore, this SA measure can be used to distinguish the figure from the ground side. We also show that no statistically significant difference exists for the lower spatial frequencies, including mean intensity.

The physical background for our observation is, we believe, the simple fact that most objects are convex. At the object boundary, surface markings on the object undergo spatial compression due to perspective projection. As a result, uniform features spread across a larger region in depth get packed into smaller viewing angles on the figure due to the surface curvature. This means, within the same viewing angle, more high frequency content is present on the figure side compared to the ground side. This only occurs in the orientation orthogonal to the boundary but not parallel to it, resulting in the observed anisotropy. This feature of the visual world has been observed previously in the spatial domain [18] and shown to be useful for FG segregation [17, 19] but ours is the first study to make use of it in the spectral domain. This is important since the effect is straightforward to quantify in spectral terms, as we show in this report. Furthermore, the computation is made very efficient by the use of Fourier techniques, and thus suitable for machine vision applications.

Given that all image data we used are taken in one way or the other by a human photographer who is likely to have controlled, among other parameters, the depth of field, an important concern is that he or she may have selected to focus on the foreground object while leaving the background blurry [42]. An algorithm for FG segregation that relies on this difference would be of limited use since it would be aided by the photographer's decision. It is therefore of importance to make sure that our algorithm does not rely on this cue. We confirmed that this is the case by three different, independent analyses.

First, we observe that differences in focus between figure and background can explain differences between the spectral powers of the figure and the ground side, the quantity we use is anisotropy on the figure side only. While a photographer may treat figure and background differently, he or she cannot control the oriented spectra (orthogonal and parallel to the OB) separately on either figure or ground since the orientation of the OB varies with each foreground object (and, of course, with each patch in each object).

Second, we are not looking for anisotropy along any arbitrary orientations on figure or ground, but along a specific set of orientations, chosen a priori. Our decision to compare spectral powers in orthogonal and parallel orientations in relation to the OB is based on theoretical considerations about statistics of the physical world [17] and on empirical psychophysics [18]. The pattern of feature gradients at the OB expected from these results will give rise to maximal differences in power between directions parallel and orthogonal to the OB, not in some other arbitrary set of orientations. This can be seen directly in the 2D mean power spectra of foreground and background patches analyzed separately. We find that the spectral power orthogonal to the OB substantially exceeds that parallel to the OB on the figure side, while there is no such difference on the background side. Results are shown in Appendix F, specifically Figure F.14. The effect is clear for both BSDS and LabelMe.

Third, we generated a subset of patch pairs by removing those in which either the foreground or the background was rendered blurry. This yielded a set of 1025 patch pairs for BSDS (out of the 1475 total) and 1716 for LabelMe (out of 1761). We then re-performed the analysis described on the remaining sharply focused patches. We essentially replicated the results obtained for the full set of patches, results are shown in Appendix E.

Together, we can conclude that the observed SA cannot be an artifact of a particular photography technique.

Another possible confound that needs to be addressed is the effect of the rotation of the image patches which is necessary to perform the Fourier transforms efficiently. Patch rotation by arbitrary angles, as is necessary due to the arbitrary orientations of the OBs, results in pixels being placed in “non-integer” locations relative to the grid defined by the image. When realigning the pixels, their values need to be interpolated. The simplest method is to replace pixel values by that of their nearest neighbors. We found that this leads to excessively jagged patches. We therefore used a simple bi-linear interpolation scheme [38] to determine the rotated pixel values. Is it possible that rotation followed by bi-linear interpolation creates a bias in the statistics? To answer this question, let us consider the effect of each operation on an isotropic field of pixels. Since rotation is a rigid transform, no bias with respect to rotation angles is introduced, so whatever was isotropic before remains isotropic after rotation. In bi-linear interpolation, the weights used for calculating the pixel value at the rotated position from its four neighbors depend on the rotation angle. But all pixels in figure and ground patches are rotated by the same angle, therefore the weights will be the same for all “new” rotated pixel locations. Hence, an isotropic field remains isotropic after bi-linear interpolation. So, a rotation followed by bi-linear interpolation transforms an isotropic field of pixels into another isotropic field, hence no bias/anisotropy is introduced by these set of operations. We also note that bi-linear interpolation has a low-pass filtering effect, as is the case to some extent with other interpolation schemes [43, 44]. But the low-pass effect in a given patch pair will be the same for both figure and ground, since both are rotated by the same amount. As our signal is the difference in high-frequency oriented powers between figure and background side, and since both sides are treated equally in the rotation process,no systematic bias is introduced.

As mentioned in the last paragraph of Section 4, one reason for our decision to analyze two different image databases (BSDS300 and LabelMe) separately was to verify that no unintentional biases were introduced in LabelMe by the human observer (S.R.) who selected patches along the object boundaries. The overall agreement in results from the two databases indicates that this is, indeed, the case. Another reason was to verify SA is not influenced by any potential bias in the type, size or quality of images. Again, consistency of results between data sets indicates that this is not the case. However, the effect of SA is less pronounced in BSDS300 than in LabelMe. The small size of BSDS300 images (≈ 0.15 megapixels) could be a possible reason, since more global information is included in the patch when image dimensions are small. The FG classification accuracy of BSDS300 images (62.5%) and that of the subset of LabelMe images which are of comparable size (< 0.5 megapixels) are very close (classification accuracy: 63.3%), further strengthening the argument.

The FG classification accuracy we obtain compares favorably with other stand-alone local cues. As we are not aware of any previous work where spectral properties of local regions on both sides of the boundary were used to make FG classifications, a direct comparison with previous work is not possible. However, the best FG classification accuracies reported in [7] for local cues such as convexity (60.1%), size (64.4%) and lower region (67.8%) are in the same range as ours. Furthermore, the method used in that study required the training of a logistic classifier model, whereas our's requires no training. Proper training has the potential to obtain better classification results. Indeed, we found that when we adopted a training-based strategy with SVM classifiers, our accuracy levels increased to 67.12% for LabelMe and 69.25% for BSDS. For the BSDS database which was used in our work as well as in [7], and for the case of a stand-alone local cue, our SVM based FG classification model performs better than all the local cues reported in [7]. On the other hand, training on realistic data sets usually requires substantial computational effort, much more than methods which can be derived directly from the statistics of natural scenes. Another advantage of methods based directly on hypotheses about natural scene statistics, without intercalation of training procedures, is that they usually allow to draw more direct conclusions about the validity of these hypotheses.

An interesting new observation is the covariance of FG classification decisions along the boundary. Since the classification is based on spectral properties of figure and ground sides, it reveals information about the variation of these properties along the boundary. Spectral properties of neighboring patches are correlated, hence there is some dependence between decisions at neighboring locations along the boundary. Beyond a certain distance (about twice the overlap of neighboring patches, r ≳ 2K), the spectral properties become essentially independent. This allows us to combine results from different locations on the same boundary to obtain more accurate results.

We finally address the question whether SA mechanisms may be exploited in biology. Spectral anisotropy captures variations in intensity gradients as well as texture variation. Both of these phenomena have a common cause – the curvature of the underlying surface. It may be possible that neurons are sensitive to such cues, meaning that they are selective to gradients in spatial frequencies. Indeed, responses of neurons in the primate parietal cortex have been reported to correlate with texture gradients compatible with 3D depth perception of tilted surfaces [45]. Responses were invariant over different types of texture patterns and most of these neurons were also sensitive to a disparity gradient, suggesting that they play an important role in the perception of 3D shapes. These or similar neuronal populations may implement the local mechanisms studied in this report and thus complement the global FG segregation mechanisms observed in extrastriate cortex [1, 8, 9]. It will be interesting to develop detailed computational models of neuronal circuitry that combine these different sources of information for FG segregation.

7. Conclusion

An analysis of spectral properties of local image patches in the context of figure ground organization is presented. The oriented high frequency spectral power distribution close to the occlusion boundary is mostly uniform in the background, whereas differences are shown to exist in the figure. For the figure side, the oriented high frequency spectral power orthogonal to the boundary exceeds that parallel to it. The figural spectral anisotropy can thus be used for figure ground discrimination. A statistical test of the ratio of orthogonal to parallel high frequency spectral powers discriminates figure from ground with 60% or greater accuracy per patch, in both datasets tested. Spectral anisotropy co-varies for close-by locations, but mostly independent over larger distances along the boundary and robust to variation in patch or image sizes.

Figure 1.

Figure ground organization with overlapping geometrical shapes. The letter F appears as figure and its boundaries are assigned to it (“owned by it”). In contrast, the ground regions do not own their borders and even if easily recognizable patterns are part of the background (see the light-colored letter G to the left of the F), they are found only through effortful scrutiny. Reproduced, with permission, from Qiu et al. [1]

Textures differ between figure and ground at occlusion boundaries in natural scenes

On the figure side, spectral power orthogonal to the boundary exceeds that along it

This asymmetry is absent on the background side

We show that this difference is a valid cue for figure-ground segregation

This local measure is easily quantifiable and it can be computed efficiently