Vacuum space charge effects in sub-picosecond soft X-ray photoemission on a molecular adsorbate layer

Abstract

Vacuum space charge induced kinetic energy shifts of O 1s and Ru 3d core levels in femtosecond soft X-ray photoemission spectra (PES) have been studied at a free electron laser (FEL) for an oxygen layer on Ru(0001). We fully reproduced the measurements by simulating the in-vacuum expansion of the photoelectrons and demonstrate the space charge contribution of the high-order harmonics in the FEL beam. Employing the same analysis for 400 nm pump-X-ray probe PES, we can disentangle the delay dependent Ru 3d energy shifts into effects induced by space charge and by lattice heating from the femtosecond pump pulse.

I. INTRODUCTION

The development of X-ray photon sources delivering femtosecond X-ray pulses, combined with the possibility of triggering chemical reactions by means of femtosecond lasers, paved the way to the realization of the surface femtochemistry dream, i.e., the possibility to follow on a femtosecond timescale the evolution of the electronic structure during a chemical reaction at a surface. By employing as a probe X-rays pulses from an X-ray free electron laser (FEL) and as a pump a femtosecond infrared laser synchronized with the probe, recent time resolved X-ray emission (XES) and time resolved X-ray absorption (XAS) experiments have shown the possibility to study simple catalytically relevant reactions at surfaces. In particular, precursor states in the desorption reaction of CO from ruthenium have been probed for the first time.¹ Moreover, it has been possible to probe the transition state of the CO oxidation reaction on ruthenium.² Along with XES and XAS, time resolved photoemission spectroscopy (PES) is an X-ray spectroscopy perfectly suited to reveal dynamical changes in the electronic structure. In fact, core level PES is a well established tool to study the physical and chemical properties of materials and allows investigation of the local charge state of an element in a complex solid as well as analysis of the chemical environment and the coordination of specific atoms.³ In order to perform femtosecond time resolved core level PES, femtosecond soft X-ray photon pulses are required as a probe. They can be produced at table top laser sources via high-order harmonic generation (HHG), i.e., by focusing an infrared laser onto a gas. Femtosecond time resolved PES experiments at HHG sources have been performed for studying surface reactions.^4–6 The major limitation of the time resolved core level PES at HHG sources is the number of photons per second in a given bandwidth that can be reached for higher photon energies. Hence, studies with HHG sources have been limited to photon energies that are usually below 100 eV. Most of the core levels like O 1s, C 1s, and N 1s that are usually probed in surface chemistry studies at synchrotrons, cannot be reached. Very recent developments have shown the possibility to achieve even higher photon energies at HHG, but this set-ups are still under development^7–10 and are far from reaching the number of photons per pulse that are readily available at FELs. FELs, in particular, with high repetition rate such as FLASH, European XFEL and LCLS II, offer therefore unique sources when it comes to the use of core level PES for femtochemistry but also in general to the study of the non-equilibrium dynamics in complex materials such as correlated systems.^11–13 However, pioneering PES experiments on solids at FELs have revealed several experimental challenges.^14–16 A very recent time resolved PES study of charge transfer on a molecular dye absorbed on a surface has shown the possibility of performing dynamical chemical analysis at FELs;¹⁷ however, the application to other systems requires a detailed study due to the difficulties in the data interpretation because of modifications in the PES spectra known as vacuum space charge effects.¹⁸ In particular, the electrons photoemitted from the sample within the duration of a femtosecond X-ray pulse can be described as enclosed in a cloud of charges originated from the sample and travelling to the analyser.¹⁸ The cloud width in the direction of the analyzer is determined by the kinetic energy distribution of the emitted electrons and the X-ray pulse length. Due to the fact that photon pulses from FELs are extremely brilliant, the electron density within the photoemitted electron cloud is very high and the electrons experience Coulomb repulsion while travelling to the analyzer. As a result, the kinetic energy distribution within the cloud is modified and this leads to shifts and broadening of the photoemission lines in measured PES spectra. The X-ray induced spectral modifications render the chemical analysis at FELs a challenging task, and the FEL beam has to be attenuated to allow for acquisition of spectra comparable to static references measured at synchrotrons. Moreover, the unavoidable strong intensity fluctuations between monochromatized X-ray pulses from self amplified spontaneous emission (SASE) FELs, like FLASH¹⁹ at DESY in Hamburg, LCLS²⁰ at SLAC in Stanford, or SACLA²¹ in Japan, lead to varying vacuum space charge conditions for each FEL pulse. Hellmann et al.¹⁵ developed methods of data analysis to overcome this problem by employing the total number of detected electrons per FEL pulse in the electron analyzer as a measurement for the photon flux and by sorting the acquired data accordingly. When performing a pump-probe experiment, a short laser pump pulse in the visible or UV is needed to trigger the dynamics under study. Such an optical pulse causes additional emission of low energy electrons that introduce pump-induced vacuum space charge effects (i.e., peak shift and broadening of the core level lines in PES spectra) that need to be considered in addition to X-ray induced vacuum space charge. In femtochemistry experiments, high pump fluences on the sample are usually required to trigger the reactions,²² therefore pump-induced vacuum space charge effects are expected to strongly influence the measurement of core level PES spectra.

Here, we report on a feasibility study of time resolved core level PES for femtochemistry experiments. We performed an optical pump (400 nm, 3.1 eV) soft X-ray probe PES experiment at LCLS on a p(2 × 1) oxygen layer chemisorbed on Ru(0001). At first, we have studied soft X-ray induced vacuum space charge effects on the kinetic energy of photoelectrons emitted from Ru 3d and O 1s core levels. By improving the data analysis scheme proposed by Hellmann et al.,¹⁵ we fully explained the kinetic energy shifts of the two core levels as a function of photon fluence and we identified the role of high harmonics contained in the FEL beam. Furthermore, we have studied the kinetic energy shift of photoelectrons emitted from Ru 3d core levels as a function of the delay between the optical pump and the X-ray probe at two different fluences. We were able to distinguish between a contribution to the spectra due to the vacuum space charge and a contribution that we associate with the lattice heating of the sample after excitation by the optical pump pulse.

II. EXPERIMENT

The experiments were performed at the soft X-ray (SXR) beamline²³ at LCLS by employing the surface science endstation (SSE). The experimental setup and sample preparation have been described in previous work.²⁴ The clean Ru(0001) single crystal was exposed at 300 K to O₂ to obtain a p(2 × 1) oxygen structure.²⁵ The LCLS was operating at 60 Hz for all presented measurements. The O 1s and Ru 3d X-ray induced vacuum space charge PES data were measured with pulses of 820 eV and 581 eV photon energy, monochromatized, focused to 300 × 300 μm² and 200 × 100 μm² and impinging on the sample at 4° to the surface plane. The optical pump-X-ray probe Ru 3d PES measurements were performed at 575 eV and 581 eV photon energy. The optical pump induced vacuum space charge effect on the emitted electrons was evaluated in two different datasets. In the first set, the optical fluence was estimated to be 70 J/m² and the laser was running at 60 Hz. Reference unpumped data were acquired through blocking the laser. The monochromatized X-ray beam was focussed to 50 × 40 μm² and the beam was impinging at 1° to the surface plane. The second dataset was acquired with 100 J/m² absorbed optical fluence. Here, the laser was running at 30 Hz and the unpumped references have been taken interleaved in the 60 Hz X-ray data. The X-ray focus here was 200 × 100 μm² and the angle of incidence of both beams was 4° to the surface plane. The optical laser pulse length was 50 fs in both cases. Despite the different beamline settings employed in the two pump-probe datasets from consecutive beamtimes which were used to enhance surface sensitivity for X-ray spectroscopy while keeping the probe fluence well below the damage threshold, the data have been acquired with comparable X-ray attenuation settings and are therefore fully comparable.

The photoemitted electrons from the sample were measured in normal emission using a VG Scienta R3000 electron analyzer working with fixed kinetic energy at pass energy 200 eV. The detector consists of a stack of MCPs, a phosphor screen, and a OPAL 1000 Adimec charge coupled device (CCD) synchronized with LCLS. For each X-ray shot, a CCD image was acquired. Only few hits (up to 60 counts) on the CCD are detected per X-ray shot. The single shot images are analyzed as in Hellmann et al.¹⁵ by identifying via a particle analysis algorithm the center of mass of each count above a pre-selected intensity threshold. The obtained positions for each count are then accumulated into a histogram by integrating over the axis perpendicular to the dispersive direction to obtain a PES spectrum. In summary, a PES spectrum and the total number of detected counts are extracted for each X-ray shot. The number of detected counts has subsequently been normalized with the respective photoemission cross sections of the measured core levels (${\sigma }_{820\hspace{0.17em}\text{eV}}(\mathrm{O}\hspace{0.17em}1\mathrm{s})=0.2\hspace{0.17em}\text{Mb},\hspace{0.17em}{\sigma }_{820\hspace{0.17em}\text{eV}}(\text{Ru}\hspace{0.17em}3\mathrm{d})=0.9\hspace{0.17em}\text{Mb}$ and ${\sigma }_{581\hspace{0.17em}\text{eV}}(\text{Ru}\hspace{0.17em}3\mathrm{d})=2\hspace{0.17em}\text{Mb}$).²⁶ Assuming a linear detector response, ensured by the pulse counting method used for analysing the single shot images,²⁷ the number of detected electrons is proportional to the total number of emitted electrons, which scales with the photon flux via the photoemission cross section. Therefore, the number of detected electrons is a photon flux measurement. To improve the statistics of single shot PES spectra (comprising up to 60 counts max), they have been accumulated after sorting the X-ray shots according to the number of detected counts. The PES spectra obtained have then been fitted with Gaussian distributions for the O 1s and the Ru 3d lines to determine their kinetic energy.

III. RESULTS AND DISCUSSION

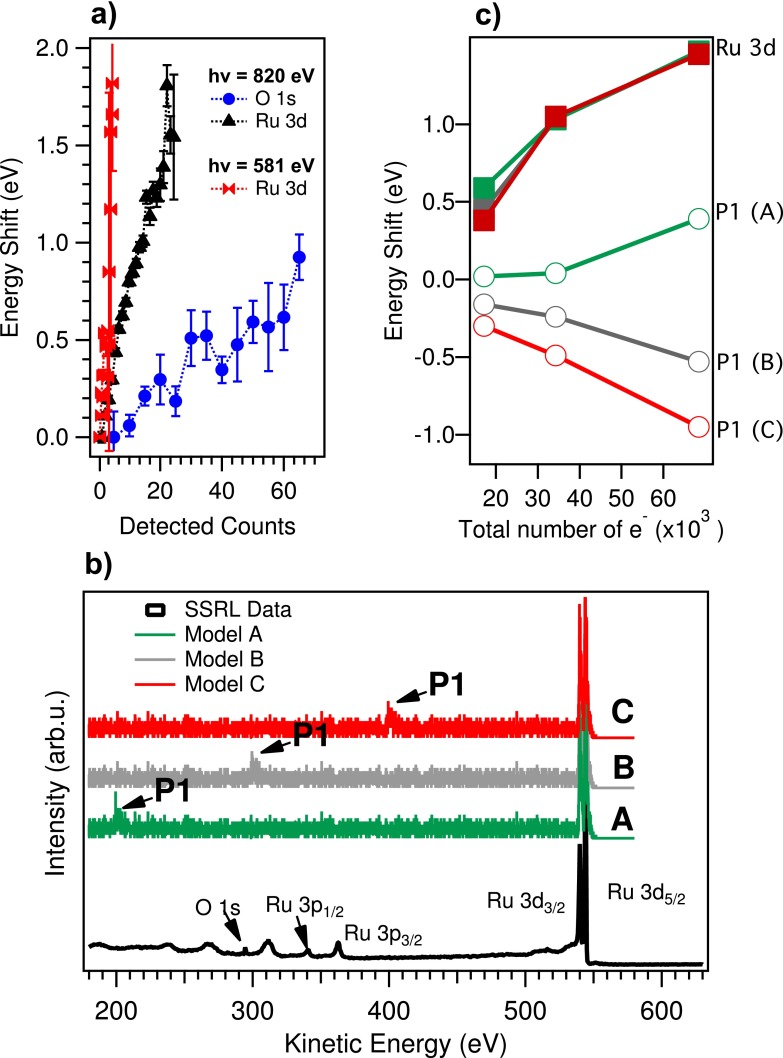
Fig. 1(a) displays the photoelectron kinetic energy shift as a function of photon flux (detected counts) for the O 1s and Ru 3d_5∕2 core levels measured with 820 eV and 581 eV photon energy, respectively. The kinetic energy of Ru 3d_5∕2 measured at 820 eV photon energy is about 540 eV. The kinetic energy of Ru 3d_5∕2 measured at 581 eV photon energy and the kinetic energy of O 1s measured at 820 eV photon energy are both about 290 eV. The energy shift in Fig. 1(a) was referenced to the lowest achievable flux measurements, i.e., one count per shot. When comparing the Ru 3d core levels measured at different photon energy, we observe, as expected, that the faster electrons (emitted with 820 eV photon energy) are less influenced by vacuum space charge. However, we also observe that the O 1s and Ru 3d measurements at 820 eV, characterized by the same total number of emitted electrons, present strong differences in their vacuum space charge shift. To understand the behavior of the different photoelectron kinetic energy shifts, the trajectories of photoelectrons emitted from the sample have been simulated by means of the ASTRA code.²⁸ In particular, an electron beam originating from a spot of 100 × 100 μm² on the sample with Gaussian momentum distribution in the surface x,y plane and normalized emittance 1 π mm mrad has been considered.²⁹ In the sample surface normal z, pointing towards the analyzer, the momentum distribution mimics the experimental spectrum, modelled by the sum of a plateau distribution and three Gaussian distributions representing the Ru 3d_5∕2, Ru 3d_3∕2, and O 1s core levels. The vacuum space charge is simulated in cylindrical symmetry with mirror charges in the sample. Particles are emitted during a 100 fs window. The initial energy distributions considered in the simulations (models A, B, and C) are compared to the synchrotron measurements performed at SSRL in Fig. 1(b). We considered a Gaussian distribution for a core level P1 at 300 eV to model the O 1s (model B), but also at 200 eV and 400 eV (models A and C) to establish how its position influences the vacuum space charge evolutions. In Fig. 1(c), the different simulated energy shifts are plotted. The shift of the Ru 3d lines is always towards higher kinetic energy independent of the position of P1 and scales nearly linearly with the total number of emitted electrons. The shift of P1 depends on its energy position as a result of the balance between the cloud of faster electrons at kinetic energies bigger than P1 that repels the slower P1 electrons and decelerates them, and the slower electrons at kinetic energies smaller than P1 that repel the P1 electrons and accelerate them. The role of the kinetic energy distribution of electrons emitted from the sample in determining the spectral modifications of the measured electrons has been shown in previous ultraviolet photoemission (UPS) work by comparing the position in UPS spectra of photoemission lines and of the secondary cut-off.^18,30 Our study is the first measurement of this effect in core level photoemission employing soft X-rays. It clearly demonstrates that when considering different core levels, e.g., for chemical composition studies, detailed simulations and a detailed knowledge of energy and momentum distribution of the photoemitted electrons are mandatory. As an example, in the presented measurements at 820 eV photon energy if we would reference all the spectra measured at the different photon fluxes to the Ru 3d_5∕2 core level lines, we would observe an energy shift of the O 1s increasing with photon flux that might be related to sample properties. We demonstrated that the shift is fully due to vacuum space charge and is not a core level shift induced by dynamic effects in the sample. We conclude that in future core level PES experiments, the data cannot be analyzed only considering the number of detected counts in the analyzer in a small energy window (i.e., the one comprising one core level), but a full characterization of the spectral distribution of all emitted electrons is necessary.

FIG. 1.

(a) Energy shift of the Ru 3d_5∕2 and O 1s core level peaks as a function of the number of counts per shot in the analyzer normalized by the photoemission cross section (detected counts). (b) Measured and simulated PES wide spectrum with one Gaussian distribution at 200 eV, 300 eV, and 400 eV, respectively (models A, B, and C) in addition to the Ru 3d lines. The Ru 3d lines of the “SSRL data” spectrum have been aligned to 544 eV kinetic energy. The spectrum was acquired with 750 eV photon energy. (c) Energy shift with respect to the initial position of the simulated core levels (labeled in the figure) as a function of the total number of electrons in the electron cloud.

A further example that the detected counts do not fully describe incoming photon flux on the sample is presented in Fig. 2. Here, the photoelectron kinetic energy shifts of the Ru 3d_5∕2 photoemission line (shown in the inset) as a function of detected counts measured for different pressures of N₂ in the LCLS gas attenuator are shown. Increasing the N₂ pressure in the gas attenuator corresponds to an overall lower incoming photon flux on the sample. However, the LCLS FEL beam contains higher harmonics.³¹ In particular, at 820 eV photon energy in the fundamental, about 0.2% of second harmonic (1640 eV) and 2% third harmonic (2460 eV) are present.³¹ The third harmonic contribution is suppressed by the SXR beamline mirrors, while the second harmonic contribution is still present at the sample position.^32,33 In Fig. 2, the estimated number of photons at the sample is reported. In particular, we considered the transmission of the 340 cm gas attenuator, the beamline efficiency^32,33 and additionally we assumed that the transmission of the second order of the monochromator is about 10% (this was estimated by considering the efficiencies at the different energies in Ref. 32). According to the analysis based on the detected electrons, spectra comprising the same number of detected counts correspond to the same photon flux on the sample. However, the Ru 3d kinetic energy increases when lowering the gas pressure in the attenuator instead of remaining constant. The experimental observation can be explained by taking into account that the higher harmonics of the 820 eV FEL radiation are not attenuated by N₂. In particular, by increasing the N₂ pressure in the attenuator from 2.2 Torr to 3.9 Torr, the first harmonic (820 eV) is attenuated by three orders of magnitude, while the second harmonic contribution in the beam decreases by only few percent. The Ru 3d counts measured in the analyzer for the different attenuator settings are generated by the first order beam (820 eV). By lowering the gas pressure, a larger second harmonic contribution in the LCLS beam causes an increasing number of electrons with high kinetic energy to be emitted, which contribute in decelerating the Ru 3d electrons created by the first harmonic and originates the measured shift.

FIG. 2.

Energy position of the Ru 3d_5∕2 core level as a function of number of detected counts for different N₂ pressures in the gas attenuator. The estimated number of photons in first and second order is also reported. For each attenuation setting, the measurement lasted between 2 and 6 min. In the inset, the measured Ru 3d lines at two attenuations (colour encoded) with four detected counts in the analyzer are plotted.

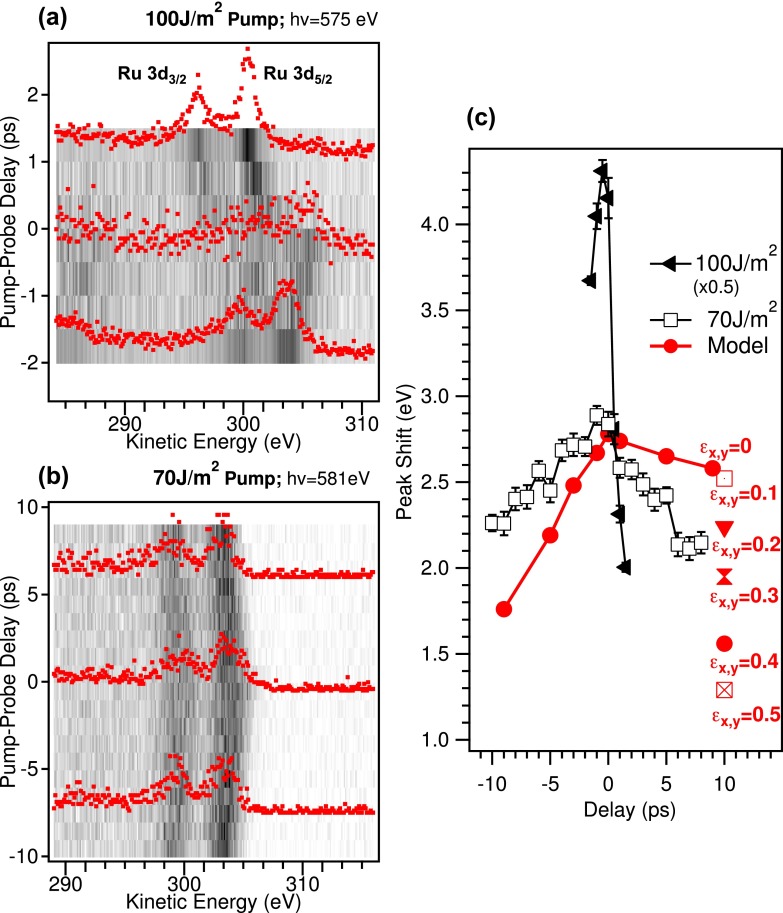
We fully understood the energy shifts of the Ru 3d and O 1s core level lines as a function of the X-ray fluence on the sample. We now move to the analysis of the pump-probe data. Figs. 3(a) and 3(b) show the measured Ru 3d_5∕2 and Ru 3d_3∕2 core levels as a function of delay between the 400 nm optical pump and the X-ray probe for two different optical fluences. The energy shift of the measured photoemission lines as a function of pump-probe delay is due to the optical pump.

FIG. 3.

Ru 3d photoemission lines as a function of pump-probe delay with optical fluence on the sample 100 J/m² and 70 J/m² ((a) and (b)). Positive pump-probe delay indicates that the probe pulse hits the sample after the pump. Spectra at selected time delays are displayed on the 2D plots. The acquisition time for each 2D plot was about 1.5 h. (c) Measured energy shift of Ru 3d_5∕2 with respect to the unpumped case in (a) and (b) (black lines). The high fluence data have been scaled by 0.5. In red, the modelled energy shift by using ASTRA for normalized emittance equal to zero is plotted, i.e., no momentum broadening on the pump ejected electrons. The energy shift at 10 ps calculated for several beam emittances (π mm mrad) is indicated by the labels close to the respective markers.

In Fig. 3(c), the difference between the fitted position of the Ru 3d_5∕2 line and its respective unpumped measurement is plotted as a function of pump-probe delay for the two pump fluences. At higher fluence, the overall shift of the photoemission lines is larger than for low fluence. In fact, more electrons are emitted by the pump pulse yielding a denser cloud that accelerates the fast X-ray emitted electrons, therefore increasing their kinetic energy. The detailed behaviour as a function of pump-probe delay is also fluence dependent. In particular, the measured energy shift is asymmetric with respect to time zero: the spectra measured after the pump pulse has impinged on the sample (positive delays) are less shifted with respect to the ones measured before the pump hits the sample (negative delays). By following the modelling described by Hellmann et al.,¹⁵ we have simulated the data with ASTRA considering electrons arising from the pump pulse due to multiphoton processes (above threshold photoemission ATP). We added a Gaussian energy distribution centered at 10 eV to the above described electron distributions employed for the X-ray vacuum space charge modelling. The additional electron distribution is a simplification of an ATP spectrum as measured, e.g., by Aeschlimann et al.³⁴ We adopted a model with a Gaussian at 10 eV because if we consider a Gaussian distribution closer to zero kinetic energy better reproducing an ATP spectrum, more electrons are lost towards the cathode during the in vacuum expansion in the simulation. To achieve the measured energy shifts we would therefore need to further increase the number of electrons in the simulation, which would then be rather time-demanding. We considered 10⁴ electrons per shot emitted from the X-rays. To achieve the energy shift of about 2 eV at time zero (as in the 70 J/m² case), 5 × 10⁵ electrons per shot at 10 eV have to be added with a normalized emittance in x and y equal to zero (ϵ_x,y). The simulated shift as a function of pump-probe delay is reported in Fig. 3(c). This model reproduces a time-dependent shift of the measured photoemission lines, however, the experimentally observed asymmetry with respect to time zero is not reproduced: the low energy electron cloud created by the 400 nm optical pump produces in the model a larger vacuum space charge effect at positive pump probe delays, because this corresponds to introducing a high density cloud of electrons before the Ru 3d electrons are ejected by the X-rays. The experimental observation can be explained if sample heating is taken into account. At 10 ps after the optical pump pulse, the induced electron and lattice temperature changes are already equilibrated and are on the order of 1000 K for the two considered fluences as can be deduced from the two-temperature model.³⁵ This enhanced sample temperature will cause a broader momentum distribution in the emitted electrons, which results in less vacuum space charge. This condition was simulated by changing the normalized beam emittance parameter of the 10 eV electrons at +10 ps. The normalized transverse beam emittance is a measurement of the electron beam phase space density that might be deduced by measuring the beam divergence at a cathode for a given spot size. For a perfectly flat cathode, the thermal emittance is defined as ${\mathrm{ϵ}}_n={\sigma }_x\frac{p_{x,rms}}{\mathit{m}\mathit{c}}$, where m is the electron mass, c is the speed of light, ${\sigma }_x=\sqrt{x^2}$ with x the electron position, and $p_{x,rms}=\sqrt{p_x^2}$ with p the momentum.³⁶ The thermal emittance therefore depends on the laser beam spot size (related to σ_x) and on the transverse momentum distribution of the photoemitted electrons. An increase in beam emittance is equivalent to an increased momentum distribution which is expected to be due to temperature effects:^37,38 the 400 nm laser adds momentum to the low energy electrons therefore increasing the thermal emission. From the trends depicted in red in Figure 3(c), it can be seen that by increasing the emittance in the simulation, the Ru 3d_5∕2 kinetic energy shift at +10 ps peak decreases with respect to negative pump-probe delays. We conclude that the measured shifts are due to vacuum space charge in the negative pump probe delay range and to combination of vacuum space charge and momentum broadening of the emitted electron distribution caused by increased temperature in the positive pump probe range.

IV. CONCLUSIONS

In conclusion, we have shown first soft X-ray PES measurements at LCLS on an adsorbate layer on a metal. We concluded that the energy shift measured for the different core level spectral lines due to vacuum space charge effects depends on the specific energy distribution of emitted electrons and not only on the total number of electrons emitted (and on the detected counts). This observation is particularly relevant in future for studies of chemical composition by means of PES, which therefore become challenging and have to be supported by appropriate data modelling. The same consideration is valid for the optical pump (400 nm)-X-ray probe photoemission measurements presented. We attribute the pump-probe delay dependent Ru 3d energy shifts to be a result of vacuum space charge and lattice heating from the femtosecond pump pulse. Both effects can be reproduced and understood by simulations. The presented vacuum space charge shifts induced by the optical pump pulse are unavoidable in femtochemistry experiments on surfaces since high optical fluences are required to trigger the chemical reactions. It is therefore mandatory to develop an appropriate data modeling.