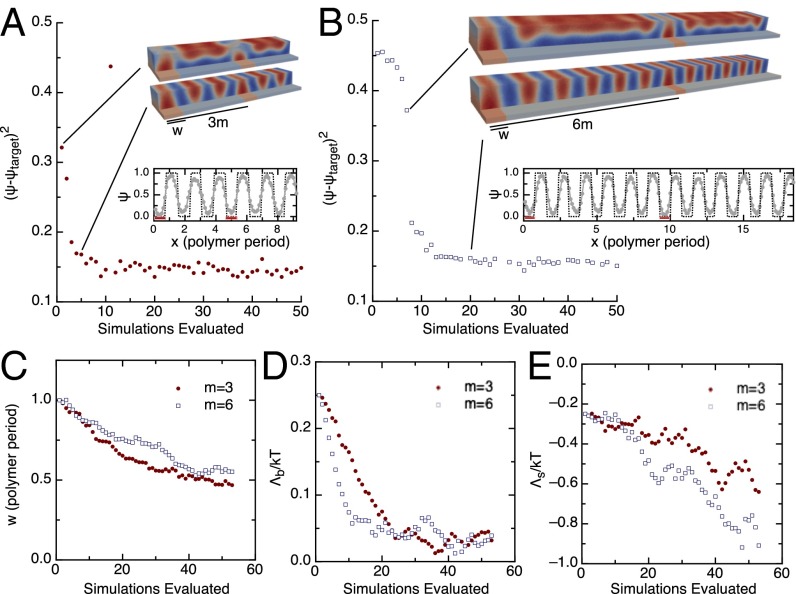
Fig. 5.

Optimizing directed self-assembly. Here we design the width of the stripe, the strength of its attraction to the red polymer beads ${\mathrm{\Lambda }}_s$, and the attraction strength of the background substrate ${\mathrm{\Lambda }}_b$ toward the blue polymer beads, to match the self-assembled phase as closely as possible to the target of alternating stripes. We quantify the success of our optimizer by comparing an order parameter $\mathrm{\Psi }\left(x\right)=\left(n_a\right)/\left(n_a+n_b\right)$ binned along the x axis of the box and averaged over y and z to the target stripe pattern. With Eq. 2, we are able to produce optimized parameters for 3× (A) and 6× (B) density multiplication after simulating 10 and 20 parameter choices. Two characteristic configurations are plotted in A and B, Insets, separated by just a handful of iterations, yet displaying markedly different phases of the polymer. Asymptotic configurations depicting Ψ (solid, marked line) and the target (dashed line) (A and B, Insets) show that the optimized parameters match the desired morphology, typically within $80\text{\%}$ or better. In plotting the parameters generated by Eq. 2 (C–E), we find that the interaction with the background brush is the most relevant parameter in directed self-assembly. For both the 6× and 3× problems, the rapid convergence toward the optimized state takes place once the background strength is reduced to ${\mathrm{\Lambda }}_b\approx 0.05$. After a weak background is established, the strip width and strength function as fine-tuning parameters that facilitate defect-free assembly.