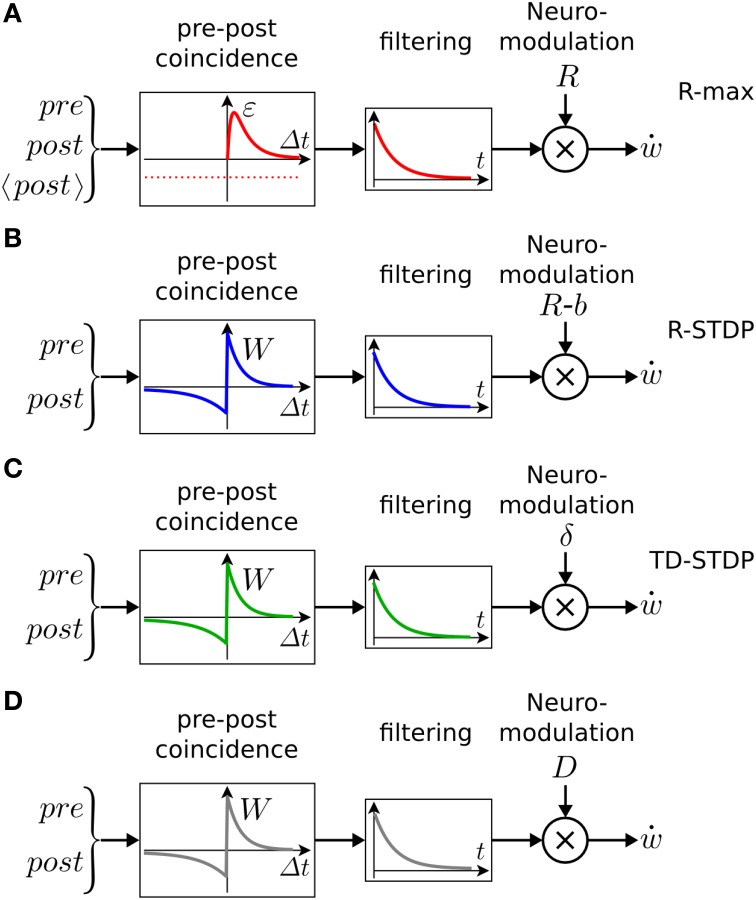
Figure 5.

Schematic of reward-modulated learning rules. Boxes on the left show the magnitude of plasticity as a function of the time difference Δt = t_post−t_pre, between post- and presynaptic spike firing. (A) R-max (Pfister et al., 2006; Baras and Meir, 2007; Florian, 2007; Frémaux et al., 2010). The learning rule is maximal for “pre-before-post” coincidences (red line, ϵ) and rides on a negative bias representing the expected number of postsynaptic spikes 〈post〉 (red dashed line). This Hebbian coincidence term is then low-pass filtered by an exponential filter, before being multiplied by the delayed reward R transmitted by a neuromodulator. (B) R-STDP (Farries and Fairhall, 2007; Florian, 2007; Izhikevich, 2007; Legenstein et al., 2008; Vasilaki et al., 2009; Frémaux et al., 2010). Similar to A, except for the shape of the pre-post coincidence window W which is bi-phasic and does not depend on the expected number of postsynaptic spikes. The Hebbian coincidence term is, after filtering, multiplied with the neuromodulator transmitting the success signal M = R − b where b is the expected reward. (C) TD-STDP (Frémaux et al., 2013). Similar to B, except for the modulating factor which in this case is the TD error M = δ^TD. (D) Generalized learning rule. Changing the meaning of the neuromodulator term M = D allows the switching between different regimes of the learning rule.