Myocardial T1 Mapping at 3.0T Using an Inversion Recovery Spoiled Gradient Echo Readout and Bloch Equation Simulation with Slice Profile Correction (BLESSPC) T1 Estimation Algorithm

Abstract

Purpose

To develop an accurate and precise myocardial T1 mapping technique using an inversion recovery spoiled gradient echo readout at 3.0T.

Materials and Methods

The modified Look-Locker inversion-recovery (MOLLI) sequence was modified to use fast low angle shot (FLASH) readout, incorporating a BLESSPC (Bloch Equation Simulation with Slice Profile Correction) T1 estimation algorithm, for accurate myocardial T1 mapping. The FLASH-MOLLI with BLESSPC fitting was compared to different approaches and sequences with regards to T1 estimation accuracy, precision and image artifact based on simulation, phantom studies, and in vivo studies of 10 healthy volunteers and 3 patients at 3.0T.

Results

The FLASH-MOLLI with BLESSPC fitting yields accurate T1 estimation (average error = −5.4±15.1 ms, percentage error = −0.5%±1.2%) for T1 from 236–1852 ms and heart rate from 40–100 bpm in phantom studies. The FLASH-MOLLI sequence prevented off-resonance artifacts in all 10 healthy volunteers at 3.0T. In vivo, there was no significant difference between FLASH-MOLLI-derived myocardial T1 values and “ShMOLLI+IE” derived values (1458.9±20.9 ms vs. 1464.1±6.8 ms, p=0.50); However, the average precision by FLASH-MOLLI was significantly better than that generated by “ShMOLLI+IE” (1.84±0.36% variance vs. 3.57±0.94%, p<0.001).

Conclusion

The FLASH-MOLLI with BLESSPC fitting yields accurate and precise T1 estimation, and eliminates banding artifacts associated with bSSFP at 3.0T.

INTRODUCTION

Myocardial T1 mapping is an emerging technique that measures T1 relaxation time for myocardial tissue characterization (1, 2). Compared to the standard late gadolinium enhancement (LGE) technique (3, 4), myocardial T1 mapping avoids potential drawbacks of conventional LGE MRI, including limited ability to detect diffuse fibrosis (5, 6), inhomogeneous radiofrequency coil sensitivity profile, and ambiguity in infarct grey zone assessment. Myocardial T1 mapping provides a promising approach to quantitative, longitudinal estimation of inter- and intra-individual diffuse alterations in myocardial tissue. Native myocardial T1 values change in the presence of a variety of pathological conditions such as acute myocardial edema (7) and amyloidosis (8). This approach enables characterization of pathologic conditions without the complications introduced by use of contrast agents.

As clinical MRI systems shift to higher field strengths for neuromuscular and body imaging (9, 10), cardiac imaging will need to adapt to higher field strengths, providing higher signal-to-noise ratio (SNR) at higher field MR for quantitative imaging.

Recent myocardial T1 mapping techniques include modified Look-Locker inversion recovery (MOLLI) (11, 12), ShMOLLI (13), SASHA (14), AIR (15), SAPPHIRE (16), and ANGIE (17) T1 mapping. These sequences are typically based on balanced steady state free precession (bSSFP) readouts, which are particularly sensitive to off-resonance banding artifacts, leading to limited utility at higher field strengths (18). The MOLLI sequence is one of the most widely used pulse sequences for myocardial T1 mapping due to the high dynamic range available using inversion preparation, high precision, and reproducibility (19–21). Proposed improvements of the MOLLI sequence include new acquisition schemes to reduce acquisition time (22), improved design of adiabatic inversion pulses, and introduction of an inversion factor correction algorithm (23) and an improved T1 estimation algorithm (24); however, a recent study using bSSFP-based MOLLI for myocardial T1 mapping at 3.0T demonstrated that at least one myocardial segment was excluded from analysis in 34 out of 59 subjects (57.6%) due to off-resonance artifacts or incorrect motion correction (25). For all 79 excluded segments in this study, 91.1% (72 segments) were excluded because of off-resonance artifacts (25).

Fast low angle shot (FLASH) imaging is more robust in limiting off-resonance artifacts than bSSFP because FLASH is a spoiled gradient echo acquisition; therefore, using a FLASH readout instead of bSSFP readout in combination with the MOLLI acquisition scheme should mitigate off-resonance artifacts for myocardial T1 mapping at 3.0T. The technique has documented promising results at 7.0T (26), with additional considerations on the inversion imperfections inherent to high field MRI; however, the “ShMOLLI+IE” sequence (26) requires a relatively long breath-hold (more than 20 heart beats), and the SNR is low at 3.0T due to a very low flip angle (5°) FLASH readout. Overall, FLASH-based myocardial T1 mapping techniques are less developed than bSSFP-based techniques, and conventional T1 calculation algorithms for a bSSFP-based readout are often not directly applicable to FLASH-based sequences.

We propose to use FLASH readouts instead of bSSFP readouts in the standard MOLLI sequence with an improved T1 mapping reconstruction approach, i.e. Bloch Equation Simulation with Slice Profile Correction (BLESSPC), for accurate and precise myocardial T1 mapping to eliminate the banding artifacts seen with bSSFP at 3.0T.

THEORY

In a standard MOLLI sequence, single-shot bSSFP images are acquired at different inversion times (TIs) using a modified Look-Locker scheme (11). Subsequently, the images are sorted according to their TIs and a 3-parameter exponential curve fitting (i.e. y = A − B exp(−TI/T1*)) is performed for each pixel. T1 is estimated using T₁ = T₁^* (B/A − 1), which is the conventional Look-Locker correction; however, the standard bSSFP-MOLLI tends to substantially underestimate T1 values (23, 27), notably due to imperfect inversion efficiency. Assuming the inversion factor δ is known, the inversion factor correction algorithm T_1corrected = T1/δ proposed by Kellman et al. (23) can be applied to improve the T1 estimation accuracy. In this manuscript, the standard fitting algorithm with Look-Locker correction and inversion factor correction is referred to as “exponential curve fitting” method.

If the readout is changed from bSSFP to FLASH in the MOLLI sequence, which is referred to as the FLASH-MOLLI sequence in this report, the T1 map calculation algorithms that have been developed for MOLLI are no longer directly applicable. Rodgers et al. (26) proposed a fitting model to improve T1 estimation accuracy for their “ShMOLLI+IE” sequence, which uses a 5° FLASH readout with linear phase-encoding order. Rodgers’ fitting method simulates the signal evolution of the sequence for T1 estimation; however, it assumes that each single-shot FLASH readout occurs instantaneously during the central k-space line, without considering each individual radiofrequency (RF) excitations or imperfect slice profile. Previous studies have documented that including the slice profile correction can generate more accurate relaxation parameter maps for Look-Locker based sequences (28, 29).

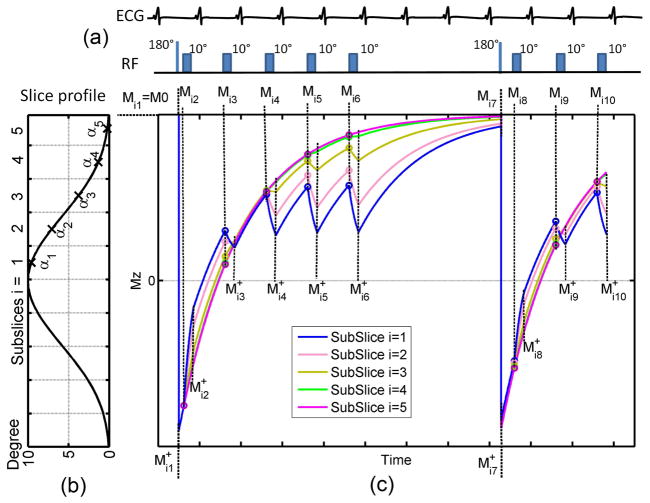
We propose a more comprehensive model - Bloch Equation Simulation with Slice Profile Correction (BLESSPC) - to calculate T1 values for each pixel. BLESSPC simulates the signal evolution of the FLASH-MOLLI sequence, and assumes that 1) the inversion pulse occurs instantaneously at the end of each inversion pulse with inversion factor δ; 2) each individual RF excitation occurs instantaneously; and 3) the transverse magnetization is completely spoiled before the next RF pulse is applied. To ensure the accuracy of the simulated signal, each pixel is evenly divided into a few sub-slices, where the sub-slice flip angle α_i is assumed to follow the expected flip angle slice profile of the RF pulse applied. Subsequently, the signal evolution of each sub-slice is simulated separately (Fig. 1).

Figure 1.

Illustration of the BLESSPC model for the FLASH-MOLLI sequence using 5-(3)-3 acquisition scheme. (a) The FLASH-MOLLI sequence acquires 8 images in 11 heart beats using a 10° single-shot FLASH readout; (b) BLESSPC divides each pixel into a few sub-slices with sub-slice flip angle α_i according to the slice profile of the RF pulse applied; (c) the longitudinal magnetization signal evolution of the FLASH-MOLLI sequence for each sub-slice. Each circle indicates the beginning of a FLASH readout. M_ij and M⁺_ij are the simulated longitudinal signals of the ith sub-slice immediately before and after an inversion pulse or a FLASH readout is applied, respectively.

Assuming an unknown T1, flip angle (α), initial magnetization M0 that we are solving for, and further assuming that the excitation pulse has a well-defined profile of sub-slice flip angles α_i due to the Fourier relationship between the RF pulse and the slice profile, the equations to calculate the signal evolution of the ith sub-slice are below.

1. The longitudinal signal immediately after an inversion, which is M_ij⁺ (j = 1or 7) in Fig. 1, is calculated by

   $${M_{ij}}^{+}=-\delta ·M_{ij}$$ [1]

   where M_ij(j = 1or 7) is the signal immediately before an inversion. The initial signal immediately before the first inversion pulse is M_i1 = M0.

2. The longitudinal signal immediately after each FLASH readout, which is M_ij⁺ (j = 2–6, 8–10) in Fig. 1, can be calculated by simulating the longitudinal signal perturbation by each individual RF pulse in a FLASH readout. To improve the processing efficiency, the following equations (Eq. [2]) are used to calculate the longitudinal signal changes due to single-shot FLASH readout in the FLASH-MOLLI sequence. These equations can be derived analytically based on Bloch equations (Appendix I).

   $$\{\begin{array}{l}{M_{ij}}^{+}=[K^{(p-1)}·M_{ij}+b]cos({\alpha }_i)\hfill \\ K=E_{1}cos({\alpha }_i),E_1=exp(-TR/T1)\hfill \\ b=M_0(1-E_1)(1-K^{(p-1)})/(1-K)\hfill \end{array}$$ [2]

   where M_ij (j = 2–6, 8–10 in Fig. 1) is the signal immediately before the first RF pulse that is applied in each single-shot FLASH readout. TR is the RF pulse repetition time and p is the number of RF pulses applied in each single-shot FLASH readout.

3. During the intervals without an inversion pulse or a FLASH readout, which are the intervals between M_i(j−1)⁺ and M_ij (j = 2,…,10 in Fig. 1), the longitudinal magnetization recovers with a T1 relaxation time. M_ij can be calculated by

   $$M_{ij}=M0+[{M_{i(j-1)}}^{+}-M0]exp[-{dt}_{(j-1)}/T1]$$ [3]

   where dt_j−1 denotes the time interval between M_i(j−1)⁺ and M_ij.

The total transverse signal M_xy(k) can be calculated as a sum over all the sub-slice signals

$$M_{xy}(k)=\sum _{i=1}^{Ns}\mathit{Mimage}(i,k)sin({\alpha }_i)$$ [4]

where Ns is the number of simulated sub-slices, Mimage(i,k) denotes the simulated longitudinal signal of sub-slice i when the k-space center point of the kth single-shot image is acquired. For centric FLASH readout, Mimage(i,1) = M_i2, Mimage(i,2) = M_i3, …, Mimage(i,8) = M_i10 in Fig. 1.

For each pixel with the actually measured signal intensity S(k) (k = 1,2,…, number of FLASH images), the model assumes that M_xy(k) is proportional to S(k), and there are four unknowns - M0, T1, α and δ - to calculate M_xy(k). We assume the inversion factor δ is known (see Inversion Factor Estimation below), which is similar to the previous work by Kellman et al. (23), and perform a 3-parameter BLESSPC fitting of M0, T1 and α. In our 3-parameter fitting model, we use the Levenberg-Marquardt (LM) algorithm to solve for the M0, T1 and α, resulting in the best match in the mean squared error between the simulated signal M_xy(k) and the measured signal S(k) for each pixel. The signal polarity for the measured signal was assigned by a phase-sensitive method (26).

Inversion Factor Estimation

In order to use the proposed 3-parameter fitting, the inversion factor δ needs to be estimated. For phantom studies, Kellman et al. (23) have shown the inversion factor matched well with simulation, therefore can be easily estimated by simulation of the inversion pulse applied; however, for in vivo studies, a previous work (24) has shown that the inversion factor on myocardium can be significantly different from the inversion factor measured in phantoms, and need to be estimated in vivo. The in vivo inversion factor was estimated using the approach previously proposed (24). Specifically, we implemented a sequence (“FLASH-MOLLI+M0”) where an additional proton density weighted image without an inversion pulse was acquired in 5 seconds (five dummy heart beats for HR = 60 bpm) following the 5-(3)-3 FLASH-MOLLI acquisition. Both the FLASH-MOLLI and M0 images were acquired during a single breath-hold. To reduce the influence of noise in the M0 image on inversion factor estimation, the additional M0 image was treated as another single-shot image with a much longer TI instead of using it as M0. Based on data from the “FLASH-MOLLI+M0” sequence, the BLESSPC 4-parameter fitting (M0, T1, α and δ) was used to estimate the average δ in vivo at the ventricular septum in a small group of subjects. The same measured inversion factor was subsequently used for all subjects participating in this study.

METHODS

Pulse Sequence

The FLASH-MOLLI pulse sequence was implemented on a 3.0T MRI scanner (Trio, Siemens Healthcare; Erlangen, Germany), which was later updated to Prisma (Siemens Healthcare; Erlangen, Germany). The traditional bSSFP-MOLLI and the “ShMOLLI+IE” sequence (26) were implemented for comparison. The acquisition scheme for FLASH-MOLLI and bSSFP-MOLLI was 5-(3)-3. For the bSSFP-MOLLI acquisitions, the shortest TIs in each inversion were chosen based on those proposed by Kellman et al. (22): 120 ms and 200 ms. When using FLASH readout, the shortest TIs in each inversion set were set to 120 ms and 320 ms. Each single-shot FLASH image for FLASH-MOLLI was acquired with a nominal flip angle (FA) = 10° and centric phase-encoding order. For “ShMOLLI+IE” sequence, an FA = 5° with linear phase-encoding order was used. For bSSFP-MOLLI, five dummy start-up RF pulses with linear flip angle increments, FA = 35°, and linear phase-encoding order was used. The following parameters were identical for all three sequences: matrix = 192 × 124, interpolated to 192 × 154, 6/8 partial Fourier acquisition, 2X GRAPPA with 36 k-space auto-calibration lines.

Simulations

To evaluate the T1 estimation accuracy of BLESSPC when compared with the exponential curve fitting technique (23) and Rodgers’ fitting method (26), detailed Bloch equation simulations of the FLASH-MOLLI signal were performed in MATLAB (the Mathworks, Natick, MA). Identical sequence parameters as described in the pulse sequence were used in the Bloch simulation: TR/TE = 3.6/1.4 ms, 64 RF excitations. The inversion factor δ was assumed to be 0.96, the T1 ranged from 200 – 1800 ms (200 ms increments), the heart rate (HR) ranged from 40 – 100 bpm (20 bpm increments), T2 = 45 ms, and nominal FA = 10°. Additionally, the effects of imperfect (non-rectangular) slice profiles of the 2D excitation pulse [duration = 480 μs, time bandwidth product = 1.6] (28, 30), RF-spoiling and gradient spoiling (31) were included in the Bloch simulations.

The standard deviation (SD) of T1 estimation for the FLASH-MOLLI sequence and the “ShMOLLI+IE” sequence was estimated by Monte-Carlo simulation with 65,536 trials using the T1s, T2s and SNRs measured from the phantom study (below) as known parameters. The estimated SD was then compared to the actual measured SD for each phantom.

Phantom Study

Eleven 50ml Agar and CuSO₄ gel phantoms with T2 = 36 ms – 71 ms, T1 = 236 ms – 1852 ms were scanned at 3.0T (Prisma) using a body phased array and the spine coil. Reference T1 values were determined by a standard inversion recovery spin-echo technique with 12 TIs (TI = 50 ms – 5000 ms), TR/TE = 10s/4.6ms. Reference T2 values were determined using a standard spin-echo technique with 11 TEs (TE = 5 ms – 250 ms). ROIs for each tube were selected, and the mean values of T1 and T2 for each tube were used as reference T1 and T2 values.

The FLASH-MOLLI source image sets were acquired with field-of-view (FOV) = 340 × 273 mm², TR/TE = 3.6/1.4 ms, interpolated pixel size = 1.8 × 1.8 mm², slice thickness= 8 mm, readout bandwidth = 511 Hz/pixel and the following two groups of parameters: (I) nominal FA = 10°, simulated ECG signals with HR = 40, 60, 80, 100 bpm, and (II) simulated ECG signals HR = 60 bpm, nominal FA = 10°,8°,6°,4°. The different FA experiments were added to study the effect of flip angle variations on the accuracy of T1 estimation, as the actual flip angle in vivo may be spatially varying due to B1 inhomogeneity.

A third group of FLASH-MOLLI images (phantom group III) were acquired with reduced FOV = 220 × 177 mm², TR/TE = 3.6/1.4 ms, interpolated pixel size = 1.2 × 1.2 mm², slice thickness= 5 mm, readout bandwidth = 722 Hz/pixel, nominal FA = 10°, and simulated HR = 60 bpm. The “ShMOLLI+IE” images were acquired with the same FOV, TR/TE, pixel size, slice thickness, readout bandwidth and HR for comparison. Both the FLASH-MOLLI and the “ShMOLLI+IE” acquisitions were repeated 15 times to assess the T1 estimation precision of these two techniques.

In Vivo Study

The study was approved by the Institutional Review Board and was compliant with the Health Insurance Portability and Accountability Act. All subjects provided written informed consent. Ten healthy volunteers (8 males, aged 28.1±3.5 years) underwent MRI using the Trio system. The “FLASH-MOLLI+M0” pulse sequence was performed on five of the ten volunteers (4 male, age 28.6±3.0 years) to establish the average in vivo inversion factor for the specific inversion pulse used in the MOLLI sequence at both the Trio and the Prisma scanner. Raw images of the mid-left ventricular short-axis were acquired at end-expiration using the FLASH-MOLLI sequence with TR/TE = 3.6/1.4 ms, slice thickness = 8 mm, readout bandwidth = 511 Hz/pixel, and the standard bSSFP-MOLLI sequence with same FOV, pixel size, TR/TE = 2.5/1.1ms, readout bandwidth = 930 Hz/pixel. The FOV was adjusted according to subject’s size and was in the range 260–400 × 209–321 mm². The other sequence parameters are described in the pulse sequence section.

Additional in vivo images were acquired using the 3.0T Prisma system (Siemens Medical Solutions, Erlangen, Germany) on both healthy volunteers and patients who underwent cardiac MRI examinations. Six of the 10 volunteers scanned on the Trio system (5 male, age 28.8 ± 3.9 years) were rescanned to evaluate the reproducibility of T1 measurement by the FLASH-MOLLI sequence. The FLASH-MOLLI sequence was performed twice with a 5 min break in between, during which time the subject was brought outside of the scanner room. The “ShMOLLI+IE” sequence scans were performed with the same FOV, TR/TE, interpolated pixel size, slice thickness and readout bandwidth. Pre- and post-contrast FLASH-MOLLI images of the mid-LV short axis were acquired in three patients (3 male, age 42.0±16.8 years). Post-contrast images were obtained about 20min after contrast agent injection. (0.15 mmol perkg body weight; Gadobenate dimeglumine, Multihance, Bracco Diagnostics, Monroe Township, NJ).

Data Analysis

T1 values or maps were generated offline using the simulated or raw image data. For simulation and phantom studies, three different T1 estimation methods (BLESSPC fitting, Rodgers’ fitting (26) and “exponential curve fitting”) were applied to generate T1 values for the FLASH-MOLLI sequence, assuming δ = 0.96 (23). The T1 estimation errors of these three different methods for the FLASH-MOLLI sequence were evaluated and compared. In addition, to evaluate the benefit of using slice profile correction with 5 sub-slices, the BLESSPC algorithm was evaluated without slice profile correction (1 sub-slice), with 5 sub-slices and with 100 sub-slices in the phantom experiments (group I), and in one of the in vivo experiments. For BLESSPC fitting of each pixel, the T1 and α fitting ranges were restricted to [10, 2500] ms and [0°, 20°], respectively, with initial values T1_initial = 800 ms, α _initial =10°, and M0 _initial = 10×S_max, where S_max represents the highest greyscale of a pixel in the raw images for all TIs. For the in vivo studies, the proposed BLESSPC fitting was used to generate T1 maps for the FLASH-MOLLI sequence. The inversion factor δ was varied for one subject to study the influence of inversion factor error on in vivo T1 estimation. For the “ShMOLLI+IE” sequence in all studies, Rodgers’ fitting (26) was used. For the bSSFP-MOLLI sequence, “exponential curve fitting” was used. Table 1 lists the corresponding T1 estimation algorithm used in the current set of experiments.

Table 1.

The T1 estimation algorithm used in the current set of experiments.

Sequence	Experiments	T1 estimation algorithm
FLASH-MOLLI	Simulation	BLESSPC vs. Rodgers’ fitting vs. exponential curve fitting
	Phantom group I	BLESSPC vs. Rodgers’ fitting vs. exponential curve fitting
	Phantom group II, III	BLESSPC
	In vivo	BLESSPC
ShMOLLI+IE	Phantom	Rodgers’ fitting
	In vivo
bSSFP-MOLLI	In vivo	Exponential curve fitting

To improve processing efficiency, the main T1 estimation algorithms were implemented using C++, and embedded in MATLAB. When generating the T1 map, only pixels with S_max > Tgreyscale were processed. Tgreyscale is a low threshold so that most of pixels in the lung and the background regions are not processed to reduce computation time. In this work, Tgreyscale was set at 8% in normalized scale [0, 1]. The coefficient of determination (R²) was used to determine the quality of the fit for each pixel. T1 values of pixels not processed or with R² < 0.98 were set to zero in the T1 map.

T1 estimation errors were calculated as T1_error = T1_cal − T1_reference and T1_error(%) = (T1_cal − T1_reference)/T1_reference × 100% for the simulation and phantom studies, where T1_cal is the calculated T1 value. For the phantom study group III, the SNR of the FLASH-MOLLI and the “ShMOLLI+IE” sequences were calculated and compared to demonstrate the benefits of being able to apply larger flip angle (10°) when using our BLESSPC fitting algorithm. The SNR calculation was based on the 5^th FLASH image (the one with longest TI in the first inversion set of images) and was calculated pixel-wise as mean signal intensity of 15 repeated measurements divided by the standard deviation. Similarly, T1 standard deviation maps were generated using 15 T1 maps generated from the repeated scans. Native myocardial T1 values were generated by manually drawing ROIs in the inter-ventricular septal (IVS) region of the in vivo T1 maps.

Results are reported as mean ± standard deviation (SD). The precision of T1 estimation in vivo was evaluated using coefficient of variation (CV = SD_ROI/Mean_ROI × 100%). The reproducibility error was calculated by $\sqrt{({\displaystyle \sum _{i=1}^{Pn}}T{1}_{\mathit{dif}}^2(i))/Pn}$, where T1_dif(i) is the T1 difference between the two repeated scans for subject number i and Pn is the number of scanned subjects. Two-tailed Student’s t tests were used for comparison, and a p value < 0.05 was considered significant.

RESULTS

Simulation and Phantom Study

For the FLASH-MOLLI sequence, the BLESSPC T1 estimation difference between using 5 sub-slices (Ns = 5) and using 100 sub-slices (Ns = 100) was small (absolute difference <0.1 ms for each pixel) in phantom studies. For T1 > 1000 ms in phantom experiments (group I), the maximum T1 estimation variations among different HRs are significantly reduced by BLESSPC T1 estimation with Ns = 5 compared to that without slice profile correction (3.8±2.0 ms or 0.2%±0.1% vs. 30.4±10.8 ms or 1.9%±0.5%, p<0.001); Therefore, Ns = 5 was used for BLESSPC fitting (Fig. 1) in this work to ensure T1 estimation accuracy while reducing processing time compared to using Ns = 100 sub-slices.

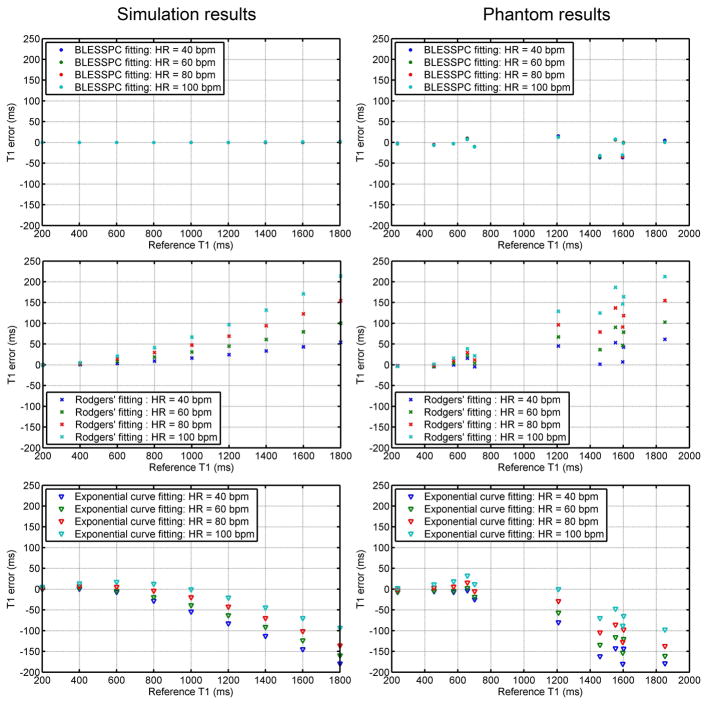
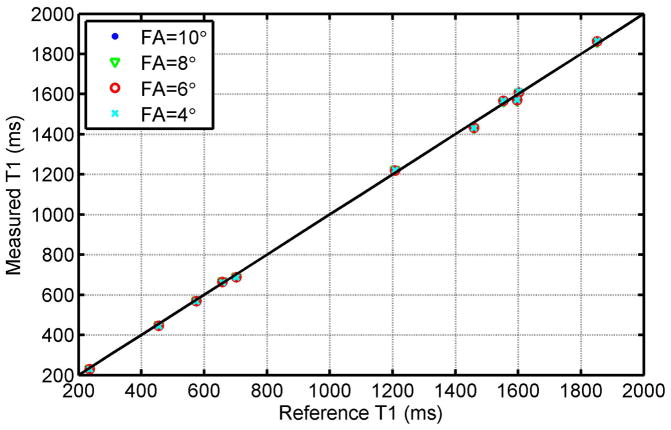
Fig. 2 shows T1 estimation errors of the three T1 estimation approaches - BLESSPC fitting, Rodgers’ fitting (26), and “exponential curve fitting” - for a range of T1 values and heart rates from simulation (left column) and phantom studies (right column) using the FLASH-MOLLI 5-(3)-3 sequence. Detailed T1 estimation results by FLASH-MOLLI with BLESSPC fitting in phantom studies are shown in Table 2 as its corresponding data points overlaps in Fig. 2. Simulation and phantom results match well for all three algorithms. The proposed BLESSPC T1 estimation algorithm provided more accurate T1 values, with much reduced sensitivity to heart rate (HR) variations when compared to Rodgers’ fitting or “exponential curve fitting” across a wide range of HRs and T1 values. Especially for T1 values > 1000ms, Rodgers’ fitting tends to overestimate T1 values, and “exponential curve fitting” tends to underestimate T1 values for the FLASH-MOLLI sequence. In the phantom results (group I), the average T1 estimation error using the proposed BLESSPC fitting was −5.4±15.1 ms (percentage error −0.5%±1.2%) with maximum absolute error of 36.9 ms for T1 ranging from 236 – 1852 ms. In comparison, the average error of Rodgers’ fitting was 55.0±60.1 ms (percentage error 3.8%±3.9%) with maximum absolute error of 212.4 ms, and that of the exponential curve fitting was −58.2±65.3 ms (percentage error −3.7%±4.3%) with maximum absolute error of 180.0 ms across the same range of T1 values. The FLASH-MOLLI sequence with BLESSPC fitting was not sensitive to RF flip angle variations (from 4° to 10°) in phantom studies (group II) [Fig. 3].

Figure 2.

T1 estimation errors by three different fitting algorithms compared to reference T1 values in both simulation and phantom studies. Phantom reference T1 values were obtained using standard inversion recovery spin-echo. The BLESSC fitting, Rodger’ fitting, and exponential curve fitting (with Look-Locker correction and inversion factor correction) approaches were applied to the FLASH-MOLLI sequence. Compared to the other two fitting methods, BLESSPC improves T1 estimation accuracy, and is insensitive to heart rate variations.

Table 2.

Measured T1 values by BLESSPC fitting in a set of FLASH-MOLLI phantom experiments (group I) with T1s 236 – 1852 ms and emulated HRs 40 – 100 bpm.

Phantom index	Ref T1(ms)	Ref T2(ms)	Measured T1 (ms) by BLESSPC fitting
			HR=40	HR=60	HR=80	HR=100	Mean
1	236	45	234	232	233	233	233±0.6
2	455	40	450	449	449	449	449±0.6
3	575	40	572	572	572	572	572±0.1
4	658	67	668	667	666	665	667±1.5
5	702	36	692	692	691	691	692±0.4
6	1208	71	1223	1220	1220	1220	1221±1.4
7	1459	39	1422	1425	1427	1427	1425±2.5
8	1553	63	1560	1559	1560	1561	1560±0.8
9	1597	38	1560	1562	1562	1566	1563±2.6
10	1602	67	1601	1602	1600	1600	1601±0.8
11	1852	67	1857	1853	1852	1852	1854±2.4

Figure 3.

The relationship between the measured T1 values using FLASH-MOLLI with BLESSPC fitting and the corresponding reference T1 values for different nominal radio frequency flip angles (FA) of the FLASH readout. The diagonal line represents the ideal identity line. Data points representing different FAs overlap each other (the blue points and green triangles cannot be seen clearly due to overlapping), indicating that FLASH-MOLL with BLESSPC T1 estimation is insensitive to flip angle variations.

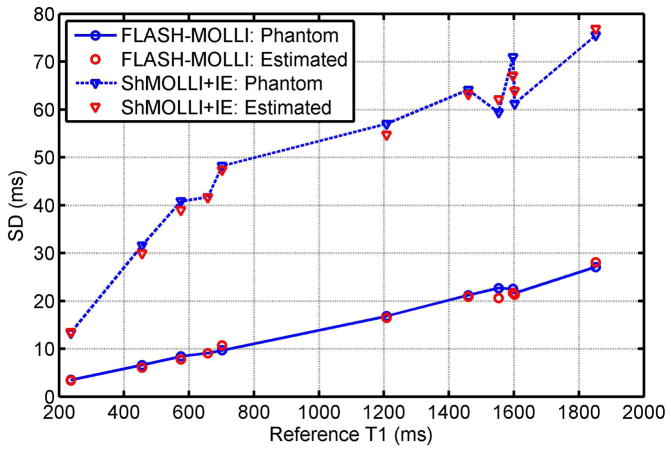
For phantom study group III, the average SNR by the FLASH-MOLLI pulse sequence was significantly higher than observed for the “ShMOLLI+IE” sequence (59.3±12.2, range [43 77] vs. 34.3±5.0, range [27 42], p<0.001). The coefficient of variation (CV) of T1 estimation for each phantom by FLASH-MOLLI with BLESSPC fitting was significantly lower than that by the “ShMOLLI+IE” sequence (1.4%±0.05% vs. 5.3%±0.13%, p<0.001). Fig. 4 summarizes SD of T1 estimation by the two sequences in phantom studies and corresponding simulation results. The simulated T1 SD matched well with measured T1 SD for both FLASH-MOLLI with BLESSPC fitting and “ShMOLLI+IE”. The SD of T1 measurement was much smaller for proposed FLASH-MOLLI with BLESSPC, indicating improved T1 estimation precision.

Figure 4.

Standard deviation (SD) of T1 measurements using the FLASH-MOLLI with BLESSPC fitting vs. “ShMOLLI+IE” in phantom experiments and Monte-Carlo simulations. Phantom results matched well with the Monte-Carlo simulations. The FLASH-MOLLI with BLESSPC fitting improved T1 estimation precision compared to the “ShMOLLI+IE” sequence.

In Vivo Study

The average inversion factor of native myocardial tissues for the inversion pulse used in the in vivo study was 0.89±0.007 in the preliminary group of five subjects with differences less than 0.005 between Trio and Prisma scanners. Subsequently, 0.89 was used as the inversion factor δ in FLASH-MOLLI and bSSFP-MOLLI for in vivo myocardial T1 mapping in 10 healthy subjects (average HR = 62.5±9.9 bpm) scanned using the Trio scanner, as well as 6 healthy subjects (average HR = 64.0±9.4 bpm) and 3 patients (average HR = 61.3±10.4 bpm) scanned using the Prisma scanner. In vivo results confirmed that the 100 sub-slices simulation did not improve the T1 estimation results compared to 5 sub-slices simulation in BLESSPC fitting (T1 absolute difference < 0.1 ms for each pixel in the entire myocardial region). The offline processing time for calculation of a T1 map (matrix = 192 × 154) on a typical desktop computer by BLESSPC (Ns=5) was less than 6 sec. The native myocardial T1 values by FLASH-MOLLI with BLESSPC fitting were significantly higher than that by the standard bSSFP-MOLLI (with inversion factor correction) by 99.0±31.7ms (1454.9±23.6 ms vs. 1355.8±23.9ms, relative 7.3%±2.4%, p<0.001). When the inversion factor used in BLESSPC fitting was increased or decreased by 0.01, the estimated T1 values decreased or increased by 19 ms (1.3%), respectively.

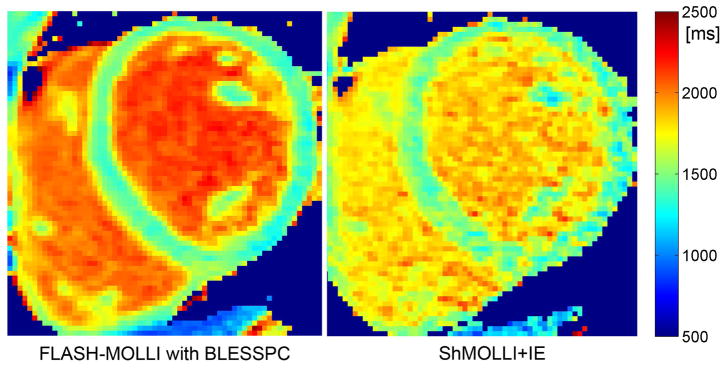
For the 6 healthy subjects (average HR = 64.0±9.5 bpm) rescanned on the Prisma scanner, there was no significant difference between the myocardial T1 values by FLASH-MOLLI and that by “ShMOLLI+IE” (1458.9±20.9 ms vs. 1464.1±6.8 ms, p = 0.50); however, the average CVs by FLASH-MOLLI were significantly lower than “ShMOLLI+IE” (1.84%±0.36% vs. 3.57%±0.94%, p < 0.001). Fig. 5 provides an example of an in vivo T1 map using FLASH-MOLLI with BLESSPC fitting (left) and a T1 map using “ShMOLLI+IE” (right) acquired from the same volunteer. The reproducibility error was 16.9 ms (1.16% of mean) for FLASH-MOLLI.

Figure 5.

Example in vivo T1 map (left) using the FLASH-MOLLI with BLESSPC fitting and (right) using “ShMOLLI+IE”. Both images were acquired from the same volunteer.

Off-resonance banding artifacts were present in six out of the ten volunteers acquired using bSSFP-MOLLI - all of which occurred in the inferior/inferolateral wall. They were absent in all ten volunteer studies using FLASH-MOLLI. Fig. 6a depicts sample images in two healthy volunteers acquired using bSSFP-MOLLI, with severe banding artifacts observed in the inferolateral wall despite careful shimming. Using the images in Fig. 6a for T1 estimation of the inferolateral wall resulted in unreliable fitting (R²<0.98), or reduced and inhomogeneous T1 values on the bSSFP-MOLLI T1 maps (Fig. 6c), especially at and around the region of banding artifacts. Using of FLASH-MOLLI resulted in homogeneous T1 maps (Fig. 6d).

Figure 6.

Example of raw bSSFP-MOLLI and FLASH-MOLLI images and T1 maps of the mid-left ventricular short-axis at 3.0T in two healthy volunteers. The raw bSSFP-MOLLI images (a) show severe off-resonance artifacts in the inferolateral wall, while the raw FLASH-MOLLI images (b) do not have artifacts. Corresponding bSSFP-MOLLI T1 maps (c) show reduced and inhomogeneous T1 values in the same region (arrow indicates region), and at extended regions beyond the locations with off-resonance artifacts while FLASH-MOLLI T1 maps (d) do not have these artifacts and have homogeneous myocardial T1 values.

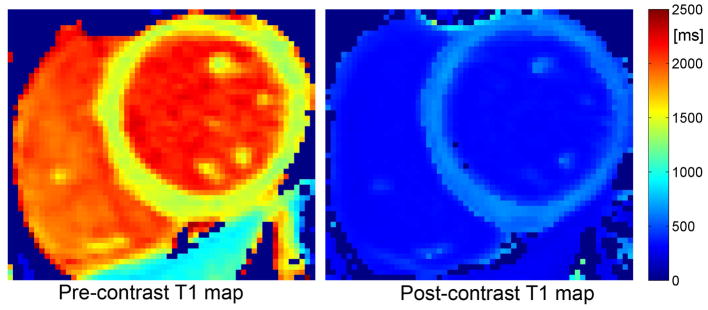
The pre- and post-contrast myocardial T1 values and CVs measured by FLASH-MOLLI with BLESSPC fitting on each patient are summarized in Table 3. Figure 7 shows an example of pre- and post-contrast T1 maps of a patient using FLASH-MOLLI with BLESSPC fitting.

Table 3.

Pre- and post-contrast myocardial T1 values and CVs of the three patients measured by FLASH-MOLLI with BLESSPC fitting

Patient	Age (years)	HR (bpm)	pre-contrast		post-contrast
			T1 (ms)	CV	T1 (ms)	CV
1	23	73	1483.7±28.1	1.89%	575.5±15.6	2.71%
2	55	58	1449.6±26.1	1.87%	629.3±16.9	2.69%
3	48	53	1477.6±27.8	1.88%	751.0±14.9	1.98%

Figure 7.

Example of pre- and post-contrast T1 maps acquired on a patient using the FLASH-MOLLI with BLESSPC fitting.

DISCUSSION

This study demonstrates the feasibility and benefits of using the FLASH-MOLLI sequence with the BLESSPC T1 estimation algorithm for accurate and precise myocardial T1 mapping at 3.0T. The primary motivation for using a FLASH readout in MOLLI at 3.0T was to avoid off-resonance banding artifacts associated with traditional bSSFP-MOLLI sequences at 3.0T. Higher SNR for FLASH-MOLLI sequences can be achieved at 3.0T relative to 1.5T. With the increasing availability of 3.0T scanners and a number of promising cardiovascular MRI applications at 3.0T - contrast enhanced MR angiography (32) and coronary imaging (33) - a robust myocardial T1 mapping sequence at 3.0T is highly desirable. The FLASH-MOLLI sequences require new T1 calculation algorithms since the fitting algorithm for bSSFP-MOLLI would is not suitable due to the much greater disturbance of the longitudinal magnetization when using FLASH readouts.

We used a FLASH readout with 10° flip angle and centric phase-encoding order, which resulted in significant T1 errors when using the exponential curve fitting or Rodgers’ fitting (26). Although Rodgers’ fitting algorithm was proposed for a FLASH-based T1 mapping sequence (“ShMOLLI+IE”), there are key differences between the BLESSPC algorithm and Rodgers’ fitting algorithm. Specifically, Rodgers’ fitting algorithm assumes that the single-shot FLASH readout occurs instantaneously during the central k-space line. This maybe a reasonable assumption at low flip angles (5°), but we found it less accurate for higher flip angle (10°) FLASH readouts with centric phase-encoding order, as demonstrated in the simulation and phantom study results. Rodgers et al. (26) have shown that using higher flip angle (>5°) does not improve the T1 estimation precision for the “ShMOLLI+IE” sequence with Rodgers’ fitting. They proposed to use a 5° flip angle, which results in much noisier images when compared to the FLASH-MOLLI sequence used in this study. In addition, our BLESSPC fitting method simulates the signal evolution of the FLASH-MOLLI sequence more accurately, taking into consideration the imperfect slice profile and the influence of each individual RF pulse on the longitudinal magnetization in single-shot FLASH readouts. Integrating detailed Bloch simulations helped the BLESSPC algorithm achieve superior T1 estimation accuracy, precision and coefficient of variation when compared with the standard exponential curve fitting or Rodgers’ fitting for FLASH-MOLLI. The BLESSPC algorithm is generally applicable to other variants of FLASH readout-based MOLLI sequences. For instance, it is possible to apply the BLESSPC algorithm to the “ShMOLLI+IE” sequence, allowing it to use a higher flip angle to achieve better precision. Using the centric phase-encoding order instead of linear phase-encoding order helps to increase image SNR.

In the BLESSPC fitting, 1, 5 and 100 sub-slices were simulated because 1 sub-slice represents T1 mapping without any slice profile correction, 5 sub-slices are our proposed approach, and 100 sub-slices were used to demonstrate that using 5 sub-slices would provide sufficiently accurate slice profile corrections when compared with 100 sub-slices, which we assume was a sufficiently large number to ensure an accurate slice profile correction. Phantom study and in vivo results show that using more than 5 sub-slices does not improve T1 estimation accuracy, and using 5 sub-slices does improve T1 estimation accuracy compared to that without using slice profile correction.

In vivo results showed that the average myocardial T1 values measured by the proposed FLASH-MOLLI with BLESSPC fitting were significantly higher than that by the bSSFP-MOLLI sequence, but there was no significant myocardial T1 measurement difference between FLASH-MOLLI with BLESSPC fitting and “ShMOLLI+IE”. The average myocardial T1 values measured using FLASH-MOLLI with BLESSPC fitting and “ShMOLLI+IE” were in better agreement with a previous study which measured native myocardial T1 (1501±69 ms) by AIR mapping (15). This was expected since it is well documented that the bSSFP-MOLLI sequence with standard exponential curve fitting tends to underestimate T1 values (23, 24), while the “ShMOLLI+IE” sequence routinely measures T1 values accurately (26). The FLASH-MOLLI achieves a T1 estimation accuracy similar to the “ShMOLLI+IE” sequence, with a much higher precision in both phantom studies results and in vivo results. BLESSPC may also be applied to the bSSFP-MOLLI sequence to improve its T1 estimation accuracy. Tissue T2 information is needed to calculate the signal evolution of bSSFP readout accurately, and the Bloch simulation for bSSFP readout would be more complex than for FLASH readout.

Previous studies have shown that RF spoiling can have large effects on the stability and accuracy of T1 estimation when using variable flip angle (VFA) FLASH-based readouts. It is important to use optimal RF phase increments for RF spoiling (34, 35). However, the effect of imperfect RF spoiling on inversion recovery (IR) T1 mapping may be much smaller than VFA-based T1 mapping. In the FLASH-MOLLI sequence, different T1 contrasts are obtained from the inversion recovery with different inversion times rather than from the actual FLASH imaging readouts where the RF spoiling is applied; whereas the VFA methods produce different T1 contrasts using a small number of flip angles for the excitation pulses and are hence more sensitive to signal variations caused by non-ideal RF spoiling during the imaging readout. Furthermore, our simulation results evaluating the effects of RF spoiling and gradient spoiling for the FLASH-MOLLI matched well with phantom results, indirectly confirming that imperfect RF spoiling, if any, does not have a significant impact on T1 estimation accuracy in our implementation.

The inhomogeneity in the RF field strength (B1) could affect the variations of actual local flip angles, which is larger at higher field strength, making it imperative to quantify the flip angle dependency of T1 mapping techniques. The FLASH-MOLLI sequence with BLESSPC fitting is not sensitive to RF flip angles changes in the range of 4° – 10°. The flip angle α for BLESSPC is calculated adaptively as an unknown parameter for each pixel; therefore, the proposed T1 estimation is relatively insensitive to B1 field variations.

Our study has limitations. Only a small number of healthy volunteers and limited number of patients are studied. A larger patient cohort validation is clearly warranted before widespread clinical utility of our technique. Although the accuracy of T1 estimation using our technique was validated and compared with gold standard inversion recovery spin-echo measurements on phantoms, there was no in vivo gold standard to validate our T1 measurements in patients. From a technical perspective, each single-shot image was acquired in the transient state in the FLASH-MOLLI sequence. The higher flip angle FLASH readout produces more image blurring, and the T1 estimation may be more sensitive to partial volume effects; therefore flip angle > 10° was not used in this study although it can potentially achieve higher SNR. The FLASH-MOLLI 5-(3)-3 was used for both pre- and post-contrast T1 mapping, which may not be optimal for post-contrast T1 mapping. The post-contrast tissue T1 is much shorter than pre-contrast tissue T1. Similar to the bSSFP-MOLLI sequence, a different sampling scheme that can sample more short TIs, such as the 4-(1)-3-(1)-2 scheme proposed by Kellman et al. (22) for bSSFP-MOLLI, may improve precision for post-contrast FLASH-MOLLI T1 mapping.

Accuracy and precision are important considerations for T1 mapping and are affected by image artifacts (18). It is well documented that bSSFP is sensitive to off-resonance artifacts at 3.0T, which has significantly limited the use of 3.0T systems for cardiac MRI. With recent advances of myocardial T1 mapping with increased spatial resolution for imaging thinner structures, such as the atrial wall (36) and the right ventricle (17), the off-resonance artifacts from bSSFP readouts are also expected to increase. This results from the longer TR that is required to achieve a higher spatial resolution. Furthermore, for patients with implanted cardiac devices, bSSFP is not suitable even at 1.5T due to severe off-resonance. In these cases, a FLASH-based T1 mapping sequence is a promising alternative when a wideband inversion is used (37). In conclusion, the feasibility of T1 mapping provided by FLASH-MOLLI with BLESSPC fitting eliminates issues due to off-resonance artifacts that are often associated with bSSFP-MOLLI at 3.0T and enable assessment of diffuse fibrosis at higher field strengths.

APPENDIX I

Denote the longitudinal magnetization immediately before and after the i^th RF pulse in the k^th single-shot FLASH imaging by Mz(k,i), Mz(k,i)⁺, and the flip angle by α. Then

$$Mz{(k,i)}^{+}=Mz(k,i)cos(\alpha )$$ [App.1]

According to Bloch equations, the relationship between Mz(k,i) and Mz⁺(k,i − 1) is

$$Mz(k,i)=M0(1-E_1)+{Mz}^{+}(k,i-1)E_1$$ [App.2]

where E₁ = exp(−TR/T1).

According to Eq. [App.1] and Eq. [App.2], the longitudinal magnetization signal prior to the last RF pulse (p^th RF pulse) of the k^th single-shot FLASH imaging

$$\begin{array}{l}Mz(k,p)=M0(1-E_1)+{Mz}^{+}(k,p-1)E_1\\ =M0(1-E_1)+Mz(k,p-1)K\\ =M0(1-E_1)+[M0(1-E_1)+Mz(k,p-2)K]K\\ =M0(1-E_1)(1+K)+Mz(k,p-2)K^2\\ =\dots \\ =M0(1-E_1)(1+K+\dots +K^{p-2})+Mz(k,1)K^{p-1}\\ =M0(1-E_1)(1-K^{p-1})/(1-K)+Mz(k,1)K^{p-1}\end{array}$$ [App.3]

where K = E₁ cos(α).

Therefore, the longitudinal magnetization signal after the last RF pulse (p^th RF pulse) of the k^th single-shot FLASH imaging is

$$\begin{array}{l}{M}^{+}(k)={Mz}^{+}(k,p)=Mz(k,p)cos(\alpha )\\ =[M0(1-E_1)(1-K^{p-1})/(1-K)+Mz(k,1)K^{p-1}]cos(\alpha )\\ =(K^{p-1}M(k)+b)cos(\alpha )\end{array}$$ [App.4]

where b = M0(1−E₁)(1 − K^p−1)/(1−K), and M(k) = Mz(k,1) is the longitudinal magnetization signal immediately prior to the first RF pulse of the k^th single-shot FLASH imaging.