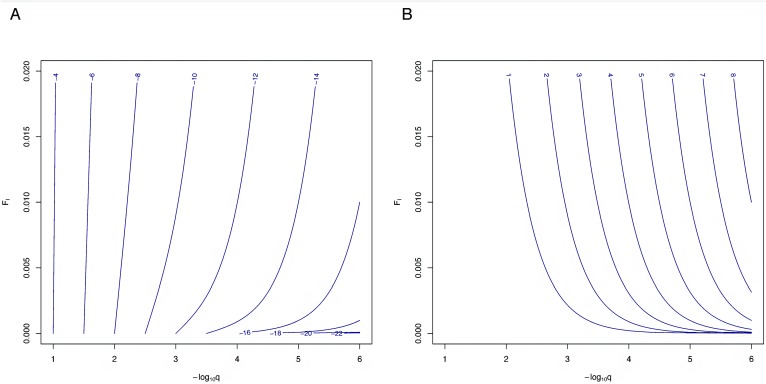
Fig 4. Co-occurrence of two recessive diseases under consanguinity.
Probabilities are calculated for a model of two recessive diseases, each being caused by a single fully penetrant locus with identical susceptibility allele frequency, q, and both loci being unlinked. (A) Log10 value of the probability to observe two recessive diseases in a single family by chance as a function of consanguinity level FI in the general population and the same risk allele frequency, q, at both unlinked loci. (B) Log10 value of the increase in the co-occurrence probability due to consanguinity compared to the non-consanguineous case (FI = 0). Probabilities and allele frequencies are depicted using their decadic logarithm (log10). For example, when assuming values of FI = 0.01 and q = 0.001 = 10−3, the two diseases will jointly occur in a single family with a probability of roughly 10−10, which equals approximately an 102 = 100-fold increase in probability in comparison to a non-consanguineous population.