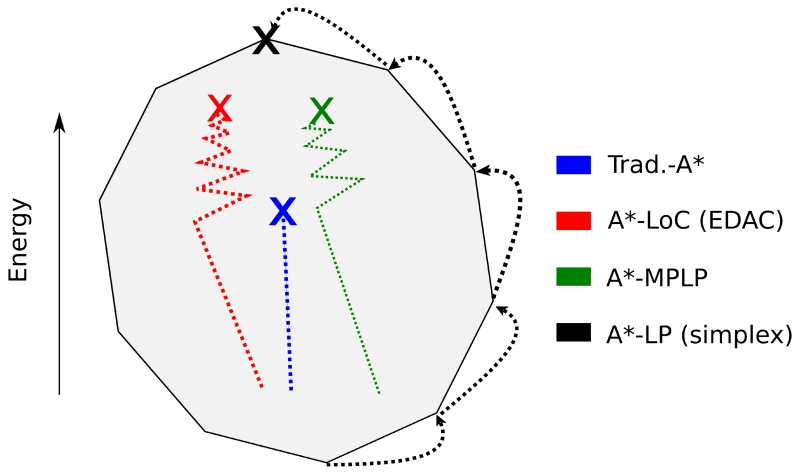
Figure A1. Several algorithms compute f-score bounds based on the dual of the protein design program.

In the relaxation of the LP formulation of the CSPD problem (the primal problem), the feasible space of solutions is a high-dimensional convex polyhedron. The dual of this formulation is also a convex polyhedron (cartooned here in 2 dimensions in grey) and any solution to the dual is a lower bound on the primal (an f-score lower bound). These f-scores can be used by algorithms, such as A* to find the optimal integer solution to the CSPD problem. The traditional A* algorithm (shown in blue) uses a simple pairwise summation (Eq. 4) to bound the protein design score. We show that the traditional A* f-score is a point in the dual of the LP and it is therefore a worse bound than the LP solution (Appendix). The EDAC algorithm [42] (red) based on local consistency and used in WCSP solvers [70], and the MPLP algorithm [38] (green) approximate the optimal LP relaxation solution. These algorithms are often more efficient than algorithms that find the exact LP solution, such as simplex (in black). Note that in this example simplex finds the optimal solution to the LP dual, which is equivalent to the optimal solution of the LP primal.