Fig. 3.

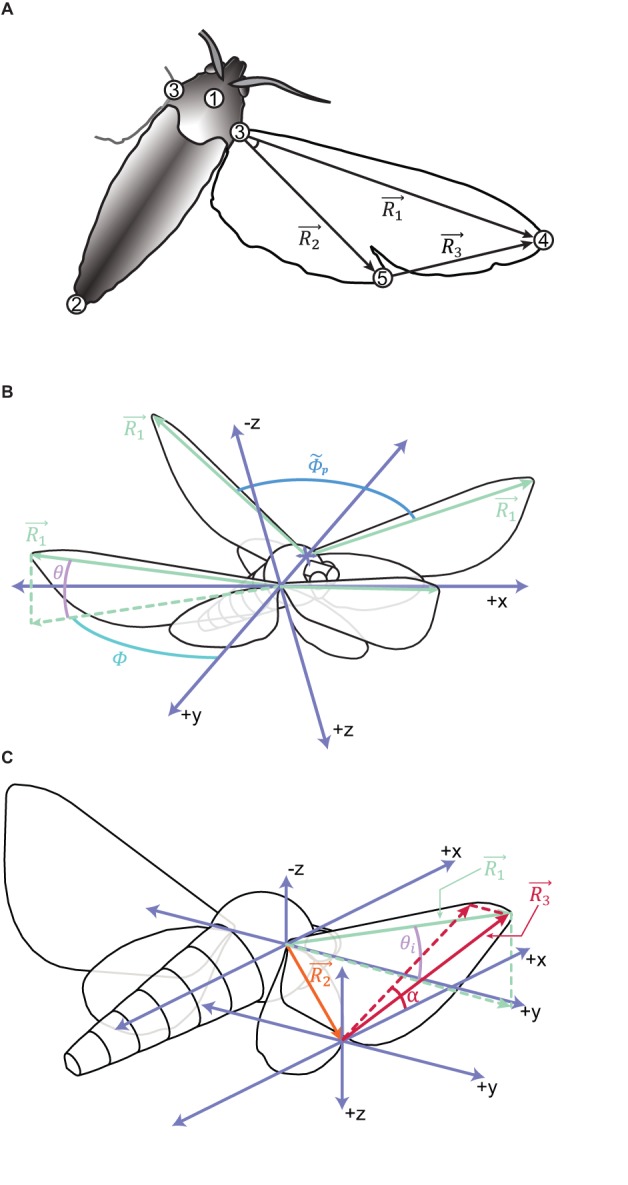
Digitization and wing angle calculation scheme. (A) Digitized points and resulting vectors used in wing position and orientation calculations. Only the body and right wing are shown in this image, but we marked points with bilateral symmetry on both sides of the sagittal plane. Point 1 was marked in an anterior portion of the scutum, point 2 at the tip of the abdomen, and point(s) 3 at the wing bases(s). We used points 1-3, measured in the GRF, to calculate yaw, pitch, and roll. These angles were then used to compute body point positions in the moth's BRF (Stengel, 2004). We next constructed an MGRF in which z remained vertical, but the x/y plane was rotated in yaw so that x was parallel with a vector running from the distal tip of the abdomen (point 2) to the geometric centroid of points 1-3, projected onto the GRF horizontal. In the MGRF, positive x movement is forwards for the moth, positive z movement is parallel with gravity (downwards), and positive y movement is to the moth's right. 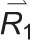is the vector which stretches from the wing base point (3) to the forewing tip (4). 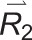is the vector which stretches from the wing base point (3) to the hindwing tip (5), and 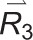stretches from (5) to (4). (B,C) To compute wing pitch angle (α), we projected 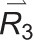onto the BRF x/z plane and took α as the angle between this projected vector and the BRF horizontal. Midstroke wing pitch angles are all positive; we measured downstroke α relative to the positive moth BRF x-axis and upstroke α relative to the negative moth BRF x-axis. θ is the angle 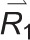makes with the BRF horizontal; at midstroke, when measured ipsilateral to the direction of roll, we call it θ_i. Peak-to-peak amplitude 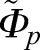is the angle between 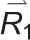's BRF position at the top of upstroke and the end of downstroke, and vv. for the following halfstroke. Sweep amplitude, Φ_p, is the projection of 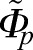onto the BRF x/y plane, while θ_p (not shown) is the projection of onto the BRF x/z plane.