Abstract.
This work focuses on volume estimation of “multidensity” lung nodules in a phantom computed tomography study. Eight objects were manufactured by enclosing spherical cores within larger spheres of double the diameter but with a different density. Different combinations of outer-shell/inner-core diameters and densities were created. The nodules were placed within an anthropomorphic phantom and scanned with various acquisition and reconstruction parameters. The volumes of the entire multidensity object as well as the inner core of the object were estimated using a model-based volume estimator. Results showed percent volume bias across all nodules and imaging protocols with slice thicknesses ranging from to 6.6% for the entire object (standard deviation ranged from 1.5% to 7.6%), and within to 5.7% for the inner-core measurement (standard deviation ranged from 2.0% to 17.7%). Overall, the estimation error was larger for the inner-core measurements, which was expected due to the smaller size of the core. Reconstructed slice thickness was found to substantially affect volumetric error for both tasks; exposure and reconstruction kernel were not. These findings provide information for understanding uncertainty in volumetry of nodules that include multiple densities such as ground glass opacities with a solid component.
Keywords: volume estimation, multidensity nodules, thoracic computed tomography, phantom study
1. Introduction
The precision and accuracy of volume estimation of lung nodules with thoracic computed tomography (CT) is affected by a number of interrelated factors including acquisition and reconstruction parameters, nodule characteristics, and measurement tools.1,2 Understanding and quantifying the effect of these factors are crucial in determining the utility of volumetric CT as a potential metric of nodule size and change in size in clinical practice. A number of studies examining the effect of such factors on nodule size estimation were summarized in a 2009 review by Gavrielides et al.1 and a recent updated review.3 In previous work, we developed a model-based volume estimator4 and applied it in a number of phantom studies to examine the effect of imaging protocols4–8 and to determine the minimum detectable change in volume.9 The use of phantom data allows for a framework where true size is known, thus allowing for the analysis of both bias and variance.
The aforementioned studies examined “solid” nodules for a wide range of radiodensities ( to 100 HU). This work focuses on volume estimation of “multidensity” nodules, constructed here as opacities of a fixed radiodensity, surrounded by an outer shell with a different radiodensity. These synthetic nodules mimic nodules with surrounding inflammation, nodules with necrotic centers, or ground glass opacities (GGO) with a solid component. Quantifying the size or change in size of such nodules is one clinical approach for long-term monitoring and evaluating response to treatment in patients with lung cancer. It is, therefore, important to examine the uncertainty in estimating the size (in this study, volume) of these types of nodules.
The purpose of this work was to quantify measurement uncertainty in the volumetric assessment of multidensity lung nodules in a phantom CT study. Analyses included both the measurement of the entire multidensity object as well as the measurement of the inner core of the object. To the best of our knowledge, this is one of the first studies examining volumetry of mixed-density nodules in either phantom or clinical studies. Related work includes the study by Scherzinger et al.,2 where nodules of the same design were used to compare the effects of exposure (40 versus 200 mAs) on solid and mixed-density nodules. In this study, we used a model-based volume estimation method instead of a segmentation method, and in addition to exposure, we examined the effects of nodule characteristics and imaging parameters including nodule size and radiodensity, slice collimation, slice thickness, and reconstruction filter. Other studies10–13 focused on the measurement of solid (uniform-density) GGOs as opposed to the mixed-density objects used in this study. The current nodule set included mixed-density nodules with low-density outer shell and high-density inner core that mimic GGOs with a solid component, as well as high-density outer shell and low-density inner shell that might mimic a low-density nodule with surrounding inflammation or a nodule with necrotizing center.
2. Materials and Methods
2.1. Anthropomorphic Phantom and Synthetic Nodules
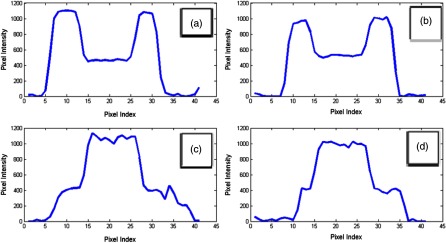
Eight synthetic spherical nodule cores were manufactured (CIRS, Norfolk, Virginia) and completely enclosed within a second larger sphere of double the diameter, but with a different density. Both the core and shell were of uniform density. Different combinations of outer/inner diameters (, ) and densities (, , , ) were created. All nodules were placed within the vasculature of an anthropomorphic phantom, as (Lungman N1, Kyotokagaku, Japan) shown in Fig. 1. Regions of interest showing central CT slices of the four outer/inner HU combinations for the nodules are shown in Fig. 2 to demonstrate the nodule properties. Corresponding axial intensity profiles are shown in Fig. 3.
Fig. 1.
(a) Photographs of the anthropomorphic phantom used in this study and (b) the inner vasculature to which synthetic nodules were attached.
Fig. 2.
Regions of interest (ROI) from CT scans of the multidensity nodules with outer/inner shell diameters of and outer/inner shell HU values of (a) , (b) , (c) , and (d) . These ROIs were extracted from scans acquired with 120 KVP, 100 mAs, 1.2 pitch, slice collimation, and reconstructed with 0.75 mm slice thickness and a b40f reconstruction kernel. In addition to the four nodules shown here, the study utilized four nodules with corresponding HU values but outer/inner shell diameters of . Note that due to the manufacturing process the spheres are not exactly concentric.
Fig. 3.
Intensity profiles acquired vertically through the inner-core centers of the multidensity nodules, as indicated with arrows in Fig. 2. Pixel intensities are related to HU values as: . It can be seen that for the nodules with outer shell of (bottom 2 nodules), a plateau for the outer shell at is not clearly visible due to the modulation transfer function of the CT system.
2.2. Imaging Protocols
The phantom was scanned with a 16-detector row CT scanner (Phillips Mx8000 IDT). Ten repeat scans were acquired per acquisition protocol using exposures of 20, 100, and 200 mAs [with corresponding values ranging within (0.9 to 1.3 mGy), (4.4 to 6.6 mGy), (8.9 to 13.2 mGy), respectively, with values varying due to different options in pitch and collimation], slice collimations of and , and a pitch of 1.2. Slice data were reconstructed with slice thicknesses of 0.8, 1.5, and 3.0 mm for the collimation and 2.0, 3.0, and 5.0 mm for the collimation, using two reconstruction filters (medium and standard), for a total of 360 reconstructed CT datasets.
2.3. Nodule Volume Estimation
There were two estimation tasks examined in this study: the estimation of the volume of the entire mixed-density nodule and the estimation of just the inner-core volume. For both tasks, object volumes were estimated from the reconstructed CT scans using a modified model-based approach based on a previously developed method for lung nodules.4 Briefly, the method minimized a cost function involving the target nodule and a bank of simulated three-dimensional nodule templates. From the reconstructed scans, volumes of interest (VOI) enclosing each of the nodules were extracted based on user-defined seed points approximately at the nodule centers. Each VOI was twice the size of the outer-shell diameter in each direction. The VOIs of the scanned synthetic nodules were matched to simulated templates of the same size. The simulated nodule templates were generated using a model of the helical multidetector CT (MDCT) imaging system (MDCT simulator), which included parameters specific to a scanner, (source-to-isocenter and source-to-detector distances, number of detector rows, detector element size), accounted for specified acquisition and reconstruction parameters, and included a forward projection of the object shape followed by filtered back projection-based image reconstruction.4 This model-based approach has the advantage of incorporating both knowledge of the nodule properties (e.g., shape and densities) and the imaging process (e.g., the image acquisition and reconstruction parameters) into the volume-estimation process.
Specific to this study, the simulated templates had the same basic geometrical structure as the nodules, with a spherical outer shell and a spherical inner core. Since the nodules did not have the exact designed radiodensities due to manufacturing imperfections, the templates were generated with inner cores and outer shells with a range of varying attenuations to capture the physical characteristics of the multidensity objects. To generate simulated templates with an outer shell of radiodensity and an inner core of radiodensity for a given mixed-density object, the procedure shown in Fig. 4 was followed.
Fig. 4.
Schematic of the mixed-density template generation process.
First, a template was simulated as a spherical object with size using an attenuation coefficient , equal to the ratio of the attenuation coefficients needed to produce the radiodensities and , defined as
where and were the linear attenuation coefficients associated with and , respectively. The linear attenuation coefficient of the background, , was assumed to be zero in this implementation. Then another template of half the size () and with a linear attenuation coefficient equal to was simulated and added to the first template. The result of the sum was a mixed-density template with a spherical object of size with an inner core of size and ratio of between the outer shell and inner core. The mixed-density template was then processed through the MDCT simulator using the same acquisition and reconstruction parameters as those used in the actual imaging process. Prior to matching (applying the cost function), the template was multiplied with the average pixel value of a neighborhood around the inner core centroid of the actual nodule to be measured, thus producing a scaled intensity profile (and values of and ) similar to that of the nodule.
Templates were generated with ranging from 70% to 130% of the target value in increments of 0.1 times the target value. For the low-density component of the nodules, a target HU value of was used for calculating instead of the designed , because HU values were observed to be consistently higher than the designed values. For the task of estimating the volume of the entire object, templates were generated with outer-shell diameters ranging from 90% to 110% of the target diameter with increments of 1%, and inner core diameters were fixed to the designed inner-core diameter. For the task of estimating the volume of inner cores, templates were generated with inner-core diameters ranging from 90% to 110% of the target diameter with increments of 1%, and outer-shell diameters were fixed to the designed nodule diameter. All templates were generated with inner cores shifted around a neighborhood, resulting in 27 templates for each size and combination, to account for the objects’ inner core and outer shell not being exactly concentric due to the manufacturing process, as can be seen in Fig. 5. The same nodule centroids were used for both estimation tasks.
Fig. 5.
Cross-section of a mixed-density nodule and a set of sample of templates used in estimating the volume of the nodule’s inner core. (a) Cross-section of a synthetic nodule (20 mm, ) outer shell and (10 mm, ) inner core, scanned at 100 mAs and reconstructed at 0.75 mm slices. (a) Template with outer shell/inner core. (c) and (d) Templates with 10 mm inner core horizontal shifted of 1, and , respectively. (e) and (f) Templates with and outer shell/inner core, respectively. The other variables used to create a complete set of templates were shifts in the vertical and axial direction, and the ratio of outer shell to inner-core radiodensities in addition to horizontal shifts and changes in the inner core to outer shell size ratio.
The sum of absolute differences cost function ( norm of the difference image) was minimized to find the best matching template.4 It was beyond the scope of this work to examine the effect that different cost functions might have on this volume-estimation task. The effect of cost function selection was examined to an extent in our previous work, and it was found that using the sum of absolute differences provided better results in terms of bias and variance compared to the sum of squared differences or normalized cross-correlation.4 The same cost function was used for both estimation tasks; the difference between the two tasks was the use of the different template banks as described earlier. For the task of estimating the volume of the entire nodule, the nodule volume of the best-matching template was used as the estimate. Similarly, the inner-core volume of the best-matching template was used as the estimate for the task of estimating the volume of the inner core.
2.4. Assessment of Volume Estimation
Prior to our analysis, all data were log-transformed (natural log) to make the data better suited for subsequent analyses such as repeated measures analysis of variance (ANOVA) which assumes homoscedasticity (equal variance across groups).14 A total of 2880 volume estimates were derived for each volume estimation task, consisting of eight measurements (eight nodules) in each of the 360 scans. From the log-transformed estimates, estimation “bias” within a group of measurements was defined as the difference between the expected value of the measurements and the measurand (true value). In our study, was defined as the nodule set and group of imaging protocols. The measurand was approximated by the reference standard value , which was based on measurements of nodule volumes from high resolution micro-CT scans. The bias on was then estimated in the log-transformed domain first as
| (1) |
where the subscript refers to the log transformation of the volume measurements, refers to the lung nodule volume measurement of the ’th nodule under the ’th imaging protocol and ’th replicate scan , and refers to the reference standard value of the ’th nodule. For easier interpretation, bias was converted into a percentage [hereafter referred to as “percent bias”(PB)] using
| (2) |
where the subscript refers to the conversion to PB. Similarly, the standard deviation of measurements in was estimated in the log-transformed domain as
| (3) |
where and equals the number of measurements in . Values were converted to percentage in the same way as in Eq. (2), and reported as standard deviation of percent error (SPE).
PB and SPE were measured for each of the eight mixed-density nodules used in the study, as well as for selected subgroups of volume estimates. Ninety-five percent confidence intervals (95% CI) of PB measures were calculated using Student’s t statistics, as implemented in the MATLAB Statistics Toolbox (version 9.0, R2014a, Mathworks, Natick, Massachusetts). The 95% CI for the SPE measures were calculated using chi statistics.
Subgroups of volume estimates were selected based on the results of n-way ANOVA with two-way interaction analysis. The individual factors included were “exposure,” “reconstruction kernel,” “slice thickness/collimation,” and “nodule size,” The factor slice thickness/collimation refers to slice thickness reconstructed from a certain detector collimation (thickness of 0.75, 1.5, and 3 mm derived from collimation and 2, 3, and 5 mm derived from ) so that the reconstructed scans with 3-mm slice thickness derived from would be distinguished from those derived using a collimation. Nodule size referred to the outer-shell/inner-core combination, which could be either or . The implemented model treated variables as fixed factors. The analysis included hypothesis testing using -statistics to determine whether each variable or interaction contributes significantly to the overall variance. “Eta-squared”15 was used for ranking substantial contribution to overall error. The eta-squared, interpreted as the proportion of the total variance that is attributed to an explanatory variable, was calculated as the ratio of the between-group sum of squares to the total sum of squares.
3. Results
The results of the ANOVA analysis, summarized in Table 1, indicated that nodule size, “slice collimation/thickness,” and the interaction of these two factors, were the most significant factors in terms of their contribution to overall variance, as indicated by achieving statistical significance and having an eta-squared value above 0.05. As such, PB and SPE were further calculated as a function of nodule size across different slice collimation/thickness values.
Table 1.
Results of N-way ANOVA analysis to determine significant factors and two-way interactions between factors. “Slice coll./thickness” refers to a slice thickness specific to a certain slice collimation. “Recon. kernel” refers to reconstruction kernel.
| Variable | -value | Eta-squared | -value | Eta-squared | ||
|---|---|---|---|---|---|---|
| Entire object | Inner core | |||||
| Nodule size | 385.6 | 0 | 0.09 | 229.8 | 0 | 0.05 |
| Slice coll./thickness | 108.5 | 0 | 0.13 | 194.1 | 0 | 0.21 |
| Exposure | 7.3 | 0.0007 | 0.6 | 0.5315 | ||
| Recon. kernel | 14.2 | 0.0002 | 1.9 | 0.1705 | ||
| 48.2 | 0 | 0.06 | 107.6 | 0 | 0.12 | |
| 5.5 | 0.0042 | 2.1 | 0.1279 | |||
| 2.9 | 0.0898 | 7.2 | 0.0075 | |||
| 3.9 | 0 | 0.01 | 5.5 | 0 | 0.01 | |
| 0.2 | 0.9638 | 0.5 | 0.7748 | |||
| 0.0 | 0.9654 | 0.00 | 0.1 | 0.8657 | 0.00 | |
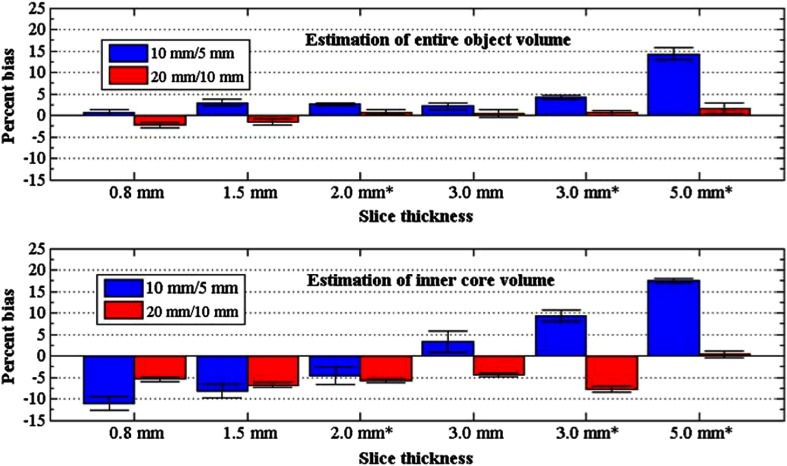
Results are listed in Table 2, specific to the two estimation tasks examined in this study, the estimation of the entire object volume and the estimation of the inner-core volume. Figures 6 and 7 show the findings of Table 2 for the analysis of PB and SPE, respectively. For these analyses, volume estimates from nodules of the same size (i.e., estimates from the four nodules with outer shell/inner core of , as well as estimates from the four nodules with outer shell/inner core of ) were pooled together. Looking at the “effect of nodule size” for the estimation of the entire object, it can be seen (Fig. 6) that the differences in PB between the and nodule sizes were in the order of 4.6% or less across slice thickness, except for scans reconstructed with 5 mm slice thickness, where the difference reached 12.7%. For the estimation of the inner core, differences in PB between the two sizes (10 and 5 mm) across all slice thicknesses were higher, ranging from 1.4% to 17.1%. Similar patterns were observed for differences between the SPE values across nodule size (Fig. 7); for the entire object task differences in SPE were in the order of 2.7% or less, whereas for the inner core task differences ranged more widely from 2.2% to 16.2%.
Table 2.
Volume estimation error across nodule size and slice collimation/thickness. Values in square brackets indicate 95% confidence intervals.
| Slice coll./thickness across nodule size | PB for entire object (95% C.I.) | SPE for entire object (95% C.I.) | PB for inner core (95% C.I.) | SPE for inner core (95% C.I.) |
|---|---|---|---|---|
| 0.7 [0.0 1.4] | 5.6 [5.1 6.1] | [] | 14.9 [13.6 16.5] | |
| [] | 5.2 [4.8 5.7] | [] | 5.1 [4.7 5.6] | |
| 3.0 [2.2 3.7] | 5.7 [5.2 6.2] | [] | 13.8 [12.6 15.3] | |
| [] | 5.6 [5.1 6.2] | [] | 5.2 [4.7 5.7] | |
| 2.2 [1.4 3.0] | 6.4 [5.9 7.1] | 3.3 [0.9 5.7] | 20.1 [18.3 22.3] | |
| 0.5 [ 1.4] | 7.0 [6.4 7.7] | [] | 3.9 [3.6 4.3] | |
| 2.6 [2.3 2.8] | 2.1 [2.0 2.3] | [] | 17.7 [16.1 19.6] | |
| 0.7 [0.2 1.4] | 4.8 [4.4 5.2] | [] | 4.2 [3.8 4.6] | |
| 4.2 [3.7 4.7] | 3.7 [3.4 4.0] | 9.3 [7.9 10.6] | 10.2 [9.4 11.3] | |
| 0.6 [ 1.2] | 5.1 [4.7 5.7] | [] | 5.8 [5.3 6.3] | |
| 14.3 [13.0 15.7] | 9.9 [9.1 10.9] | 17.5 [17.0 18.1] | 3.8 [3.5 4.2] | |
| 1.6 [0.4 2.8] | 9.6 [8.8 10.6] | 0.4 [ 1.1] | 6.0 [5.5 6.6] |
Fig. 6.
PB across slice thickness for the two nodule sizes used in the study (outer-shell/inner-core combinations of and ). Slice thickness values were based on slice collimation of except from those indicated with * (slice collimation of ). Top plot refers to the estimation of the entire object volume; bottom plot refers to the estimation of the inner-core volume. Error bars indicate 95% confidence intervals.
Fig. 7.
SPE across slice thickness for the two nodule sizes used in the study (outer-shell/inner-core combinations of and ). Slice thickness values were based on slice collimation of except from those indicated with * (slice collimation of ). Top plot refers to the estimation of the entire object volume; bottom plot refers to the estimation of the inner-core volume. Error bars indicate 95% confidence intervals.
Looking at the “effect of slice collimation/thickness,” it can be seen from Fig. 6 that for the task of estimating the entire object volume, PB varied mildly within the range of to 4.6% with varying slice collimation/thickness, with the exception of measuring the smaller nodules () using the 5 mm slice thickness scans, where PB reached 14.3%. However, the effect of slice collimation/thickness was more pronounced for the estimation of the inner core; PB varied in the range of to 17.5% across slice collimation/thickness for the smaller nodules (). The effect was less pronounced for the nodules where PB varied within to 0.5%. Regarding variance, it can be seen from Fig. 7 that SPE values spanned a wider range (3.8% to 20.1%) across slice collimation/thickness in the inner-core measurement of the nodules compared to the entire object measurement (5.2% to 7.0%). For the nodules, smaller SPE differences were observed across slice collimation/thickness as well as across the entire object and inner-core measurements.
For the estimation of the inner core, neither exposure [the “product of tube current and time” (mAs)] nor reconstruction kernel were found to be statistically significant individual factors in the ANOVA analysis (Table 1). These two factors were found to be statistically significant for the estimation of the “entire object,” but their effect (based on eta-squared values) was small compared to the effect of nodule size and slice collimation/thickness.
In terms of bias and variance, exposure and reconstruction kernel showed small differences (not shown in Table 2) between settings for PB (in the order of 1% or less) and SPE (in the order of 1.6% or less). The results regarding exposure were in line with the reported results by Scherzinger et al.2 on nodules of the same design in that volumetric bias was not influenced by changes in CT dose.
In addition to the analysis of PB and SPE across the most significant factors (nodule size and slice collimation/thickness), values of PB and SPE were calculated for each of the eight nodules used in our study. Results are shown in Tables 3 and 4, for the estimation of the outer shell and inner core, respectively. For this analysis, estimates were pooled across all imaging protocols, except from the 5 mm slice thickness which was shown in the analysis above to produce substantially higher PB and wider 95% C.I for the nodules.
Table 3.
Entire object volume estimation results for the multidensity synthetic lung nodules. Results were derived from volume estimates pooled together across all different imaging parameters except for the 5 mm slice thickness (300 total measurements for each object). Values in square brackets indicate 95% confidence intervals.
| Object | Outer-shell/inner-core characteristics | Volume estimation results for entire object | ||
|---|---|---|---|---|
| Diameter | Radiodensity (HU) | PB | SPE | |
| 1 | 0.1 [ 1.0] | 7.6 [7.1 8.3] | ||
| 2 | 3.2 [2.8 3.5] | 3.1 [2.9 3.4] | ||
| 3 | 4.9 [4.4 5.3] | 3.8 [3.5 4.2] | ||
| 4 | 2.4 [2.1 2.7] | 2.8 [2.6 3.1] | ||
| 5 | [] | 3.1 [2.8 3.3] | ||
| 6 | [] | 1.5 [1.4 1.7] | ||
| 7 | 2.1 [1.7 2.5] | 3.5 [3.3 3.8] | ||
| 8 | 6.6 [6.4 6.9] | 2.5 [2.3 2.7] | ||
Table 4.
Inner core volume estimation results for the multidensity synthetic lung nodules. Results were derived from volume estimates pooled together across all different imaging parameters except for the 5 mm slice thickness (300 total measurements for each object). Values in square brackets indicate 95% confidence intervals.
| Object | Outer-shell/inner-core characteristics | Volume estimation results for inner core | ||
|---|---|---|---|---|
| Diameter (mm) | Radiodensity (HU) | PB | SPE | |
| 1 | [] | 17.7 [16.4 19.2] | ||
| 2 | [] | 16.2 [15.0 17.6] | ||
| 3 | 5.0 [4.0 6.0] | 8.8 [8.2 9.6] | ||
| 4 | 5.7 [4.4 6.7] | 9.2 [8.5 10.0] | ||
| 5 | [] | 4.5 [4.2 4.9] | ||
| 6 | [] | 4.5 [4.2 4.9] | ||
| 7 | [] | 2.0 [1.9 2.2] | ||
| 8 | [] | 3.1 [2.9 3.4] | ||
Table 3 lists results for estimating the volume of the entire object for each of the mixed-density nodules. Results show PB values across all nodules and imaging protocols ranging from to 6.6% and SPE values ranging from 1.5% to 7.6%. In related work by Scherziger et al.,2 a segmentation-based method was applied to nodules of the same design as those in our study. Results showed relative bias in the order of 15% (standard deviation in the order of 20%). The relative increase in bias and variance compared to the results seen in our study could be due to the use of a segmentation method; in related work, Li et al.16 reported differences of similar magnitude between the estimation error using this model-based approach and a segmentation method. No substantial trends specific to the different outer-shell/inner-core radiodensity combinations were observed.
Values of PB and SPE for estimating the volume of the “inner core” for each of the mixed-density nodules are tabulated in Table 4. Results show PB values across all nodules and imaging protocols ranging from to 5.7% and SPE values ranging from 2.0% to 17.7%. The range of PB was larger and the values of SPE were higher for the inner-core measurement. Both findings are in line with literature findings that volumetric estimation error decreases with increasing nodule size.1 Again, no trends specific to the different outer-shell/inner-core radiodensity combinations were observed.
4. Discussion
The above results regarding factors affecting lung nodule volumetric error provide further evidence to literature findings1 regarding the interaction of slice thickness with nodule size; it can generally be concluded that nodules with diameters of can be measured with reasonable bias and variance using slice thickness , whereas subcentimeter nodules should preferably be measured with slice thickness .
Our study had some limitations. The implementation of the model-based estimation method utilized in our study was not ideal, since it assumed that the inner cores were either concentric or offset by an integer pixel in relation to the entire object; for some nodules this assumption was not true, thus creating a small measurement bias. By design, the model-based estimator was informed of the nodule’s shape. As such, it had an advantage over segmentation methods that do not have this information available. In theory, this model-based estimator would yield estimates with low bias so the identified factors affecting lung nodule volume measurements would likely be from the nodule and the CT system themselves and less dependent on the volume estimation method compared to using a segmentation algorithm. In that context, the results in this study are intended to approximate a lower bound on estimation error. Second, in the estimation of the entire object or inner core, the corresponding inner core or entire object sizes, respectively, were held constant. The reason for not simultaneously varying both the outer-shell and inner-core diameters was that it was too computationally intensive considering that and the templates’ centroids were also varied. Varying the sizes of those components, e.g., the entire object when measuring the inner core, could affect the choice of the matching template. It has to be noted that our volume estimation method was not intended for application to clinical nodules, but only for quantifying and ranking the different factors affecting volumetric CT. In future work, we will address the impact, in terms of estimation error, of providing the estimator with less information regarding the nodule properties, such as not providing the nodule shape.
Another limitation of the study is the lack of parenchyma in the phantom lung. As such, the error values reported here might be different when measurements are made of nodules with lower contrast-to-background ratios or when using different volume estimation methods. Additionally, this work was limited to spherical objects (both the entire and inner core) and did not address issues related to complexity in nodule shape. Finally, the CT scans used in our study were acquired using a single Phillips scanner. Although there is no a priori reason why these results would not generalize to other scanners, additional studies would still be useful to verify the generalizability of these results to other scanners.
Overall, the results show that the volume of different components of multidensity nodules can be measured with relatively small error (PB on the order of less than ) when accounting for the heterogeneous nature of the nodule. This finding is comparable to results from our previous work4,6 that focused on single-density spherical nodules with diameters ranging in size between 5 and 20 mm and densities of to 100 HU, and showed absolute PB of 9.1% or less. As a point of reference, the quantitative imaging biomarkers alliance profile for CT-based lung tumor volume change claims that “there is a 95% probability that the measured change within the range of to encompasses the true tumor volume change.”17 As expected, the PB seen in our study was less than the 30% value due to less complex nodules and surrounding background in our phantom compared to clinical nodules and the use of a model-based estimation method that was designed to indicate a lower bound of estimation error.
As part of our ongoing effort to share data,18 the CT datasets used in this study will become publicly available through the Cancer Imaging Archive in 2016 (as part of the Phantom FDA collection), along with corresponding digital object identifier.
5. Conclusions
The results show that the volumes of different components of multidensity nodules can be measured with relatively small error (PB on the order of less than ) when accounting for the heterogeneous nature of the nodule. These findings provide information for understanding uncertainty in clinical measurements of nodules that include components of different densities such as GGO with a solid component.
Acknowledgments
This work was supported in part through a Critical Path grant from the U.S. Food and Drug Administration (FDA). The CT scanner used in the study was made available through an Interagency Agreement between the Center for Interventional Oncology at the National Institutes of Health and the FDA. The mention of commercial entities, or commercial products, their sources, or their use in connection with material reported herein is not to be construed as either an actual or implied endorsement of such entities or products by the Department of Health and Human Services or the U.S. FDA.
Biographies
Marios A. Gavrielides received a PhD in biomedical engineering from Duke University in 2001. He is currently a staff scientist with the Division of Imaging, Diagnostics, and Software Reliability, Office of Science and Engineering Laboratories, Center for Devices and Radiological Health at the Food and Drug Administration in Silver Spring, Maryland. His research interests include the development and assessment of quantitative imaging methodologies, with emphasis on volumetric computed tomography, digital pathology, and computer-aided diagnosis.
Qin Li is a postdoc in the Division of Imaging, Diagnostics, and Software Reliability at the U.S. Food and Drug Administration. Her current research interests include image quality assessment and evaluation of quantitative imaging biomarker with a focus on CT.
Rongping Zeng is a research scientist in the Office of Science and Engineering Laboratories, Center for Devices and Radiological Health within the Food and Drug Administration in USA. Her research interests include objective image quality assessment, image reconstruction and image processing, quantitative imaging for CT, and breast tomosynthesis.
Kyle J. Myers received her bachelor’s degrees in mathematics and physics from Occidental College in 1980 and a PhD in optical sciences from the University of Arizona in 1985. She has worked for FDA’s Center for Devices and Radiological Health, where she currently heads the Division of Imaging, Diagnostics, and Software Reliability, since 1987. She is a fellow of OSA, SPIE, and AIMBE and a member of the National Academy of Engineering.
Berkman Sahiner, PhD, is a senior biomedical research scientist at the Division of Imaging, Diagnostics and Software Reliability within the U.S. Food and Drug Administration, Center for Devices and Radiological Health. His research interests include computer-aided diagnosis, quantitative imaging, image analysis, breast imaging, image perception, and performance assessment methodologies.
Nicholas Petrick received his PhD in electrical engineering from the University of Michigan, in the area of medical imaging systems. He is currently the acting director of the Division of Imaging, Diagnostics and Software Reliability at the Center for Devices and Radiological Health, U.S. Food and Drug Administration and holds an adjunct appointment in the University of Michigan Medical School. His research interests include quantitative imaging, computer-aided diagnosis, and assessment methods for medical imaging devices.
References
- 1.Gavrielides M. A., et al. , “Non-calcified lung nodules: volumetric assessment with thoracic CT,” Radiology 251(1), 26–37 (2009). 10.1148/radiol.2511071897 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Scherzinger A., et al. , Quantitative Measurement of Part-Solid Nodule Size on CT in a Chest Phantom: Effect of Dose on Accuracy, RSNA, Chicago, Illinois: (2013). [Google Scholar]
- 3.Gavrielides M. A., et al. , “Volumetric analysis of non-calcified lung nodules with thoracic CT: an updated review of related work over the last 5 years,” J. Radiol. Radiat. Ther. 2(2), 1040 (2014). [Google Scholar]
- 4.Gavrielides M. A., et al. , “Information-theoretic approach for analyzing bias and variance in lung nodule size estimation,” IEEE Trans. Med. Imag. 29(10), 1795–1807 (2010). 10.1109/TMI.2010.2052466 [DOI] [PubMed] [Google Scholar]
- 5.Gavrielides M. A., et al. , “A template-based approach for the analysis of lung nodules in a volumetric CT phantom study,” Proc. SPIE 7260, 726009 (2009). 10.1117/12.813560 [DOI] [Google Scholar]
- 6.Gavrielides M. A., et al. , “Benefit of overlapping reconstruction for improving the quantitative assessment of CT lung nodule volume,” Acad. Radiol. 20(2), 173–180 (2013). 10.1016/j.acra.2012.08.014 [DOI] [PubMed] [Google Scholar]
- 7.Li Q., et al. , “Volume estimation of low-contrast lesions with CT: a comparison of performances from a phantom study, simulations and theoretical analysis,” Phys. Med. Biol. 60, 671–688 (2015). 10.1088/0031-9155/60/2/671 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Li Q., et al. , “Statistical analysis of lung nodule volume measurements with CT in a large-scale phantom study,” Med. Phys. 42(7), 3932–3947 (2015). 10.1118/1.4921734 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Gavrielides M. A., et al. , “Minimum detectable change in lung nodule volume in a phantom CT study,” Acad. Radiol. 20(11), 1364–1470 (2013). 10.1016/j.acra.2013.08.019 [DOI] [PubMed] [Google Scholar]
- 10.Oda S., et al. , “Computer-aided volumetry of pulmonary nodules exhibiting ground-glass opacity at MDCT,” Am. J. Roentgenol. 194(2), 398–406 (2010). 10.2214/AJR.09.2583 [DOI] [PubMed] [Google Scholar]
- 11.Doo K. W., et al. , “Accuracy of lung nodule volumetry in low-dose CT with iterative reconstruction: an anthropomorphic thoracic phantom study,” Br. J. Radiol. 87(1041) (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Linning E., Daqing M., “Volumetric measurement pulmonary ground-glass opacity nodules with multi-detector CT: effect of various tube current on measurement accuracy—a chest CT phantom study,” Acad. Radiol. 16(8), 934–939 (2009). 10.1016/j.acra.2009.02.020 [DOI] [PubMed] [Google Scholar]
- 13.Siegelman J. W., Supanich M. P., Gavrielides M. A., “Pulmonary nodules with ground-glass opacity can be reliably measured with low-dose techniques regardless of iterative reconstruction: results of a phantom study,” Am. J. Roentgenol. 204(6), 1242–1247 (2015). 10.2214/AJR.14.13820 [DOI] [PubMed] [Google Scholar]
- 14.Raunig D. L., et al. , “Quantitative imaging biomarkers: a review of statistical methods for technical performance assessment,” Stat. Methods Med. Res. 24, 27–69 (2014). 10.1177/0962280214537344 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Cohen J., “Eta-squared and partial eta-squared in fixed factor ANOVA designs,” Educ. Psychol. Meas. 33(1), 107–112 (1973). 10.1177/001316447303300111 [DOI] [Google Scholar]
- 16.Li Q., et al. , “Factors affecting uncertainty in lung nodule volume estimation with CT: comparisons of findings from two estimation methods in a phantom study,” Proc. SPIE 9414, 94140C (2015). 10.1117/12.2081489 [DOI] [Google Scholar]
- 17.CT Volumetry Technical Committee, “CT tumor volume change profile, quantitative imaging biomarkers alliance,” version 2.2, Reviewed Draft, QIBA, 2012, https://www.rsna.org/uploadedFiles/RSNA/Content/Science_and_Education/QIBA/QIBA_CT%20Vol_TumorVolumeChangeProfile_v2.2_PubliclyReviewedVersion_08AUG2012.pdf.
- 18.Gavrielides M. A., et al. , “A resource for the assessment of lung nodule size estimation methods: database of thoracic CT scans of an anthropomorphic phantom,” Opt. Express 18(4), 15244–15255 (2010). 10.1364/OE.18.015244 [DOI] [PMC free article] [PubMed] [Google Scholar]