Abstract
The present study employed data simulation techniques to investigate the one-year stability of alternative classification schemes for identifying children with reading disabilities. Classification schemes investigated include low performance, unexpected low performance, dual-discrepancy, and a rudimentary form of constellation model of reading disabilities that included multiple criteria. Data from Spencer et al. (2014) were used to construct a growth model of reading development. The parameters estimated from this model were then used to construct three simulated datasets wherein the growth parameters were manipulated in one of three ways: A stable-growth pattern, a mastery learning pattern and a fan-spread pattern. Results indicated that overall the constellation model provided the most stable classifications across all conditions of the simulation, and that classification schemes were most stable in the fan-spread condition, and were the least stable under the mastery learning growth pattern. These results also demonstrate the utility of data simulations in reading research.
How can we determine if someone has a reading disability? An answer to this question is fundamentally important to helping individuals with reading problems and for making advancements in research. Yet there is no consensus on the best approach for identifying and classifying students with a reading disability. The inability to consistently identify students with a reading disability puts a strain on families, teachers and schools, because without accurate classification it makes it hard to help children struggling to read. Researchers are actively proposing and testing different models and classification schemes that would identify children as having a reading disability, however these models have shown low to moderate agreement with each other in terms of who gets identified (Spencer et al., 2014). Perhaps the most widely used model of reading disability has been the aptitude-achievement model in which reading disability is defined by a significant discrepancy between aptitude, which serves as an estimate of expected level of achievement in reading, and achievement in reading (Bateman, 1965). This approach has been criticized on a number of reasons, including the argument that differences between aptitude-achievement discrepant poor readers and poor readers without such a discrepancy are minimal (see Fletcher, Lyon, Fuchs, & Barnes, 2007 for a review). A potential replacement for the aptitude-achievement model has been a response-to-intervention model in which a reading disability is defined by a poor response to instruction and intervention (D. Fuchs & L. Fuchs, 2006). Finally, “hybrid” models have been proposed in which multiple sources of information are used to define reading disability (Bradley, Danielson, & Hallahan, 2003; Fletcher et al., 2013; Spencer et al., 2014; Wagner, 2008).
Research into these classification schemes indicate that their ability to identify the same students as being disabled is moderate to poor (Brown Waesche et al., 2011) and that the longitudinal stability within each classification is also very low. Brown Waesche et al. (2011) investigated rates of agreement and longitudinal stability of alternative definitions of reading disabilities in a large statewide database of over a quarter of a million children. In this study, operational definitions of discrepancy models and two forms of RTI models were developed and students were identified as being reading disabled based upon these classification schemes. Agreement among the different schemes was moderate to poor, with agreement indices ranging from as low as 8% and with many of the agreement rates below 50%. The longitudinal stability within each classification was even lower, with almost all of the agreement rates below 50% and none of them higher than 58%. Finally, Brown Waesche et al. (2011) also demonstrated that as the cut-score used to identify students decreased, the agreement rates across classifications and longitudinal stability decreased.
Barth et al. (2008) also found the same pattern of low agreement among different RTI classification schemes in a sample of 399 first graders. Students were classified as non-responders based upon either dual-discrepancy models, low-growth models, or normalization models. Barth et al. (2008) reported classification agreements in the 50% range among those identified by at least one method as being a nonresponder, however these agreements were found when the cut-score was only one-half a standard deviation below the mean and this liberal cut-score produced an incidence rate that identified over half the sample. When using a more stringent cut score of one full standard deviation below the mean, the agreement rates dropped into the 30% range.
Spencer et al., (2014) investigated the longitudinal stability of alternative classification schemes in a dataset of 31,000 first and second grade students who had been assessed four times in each grade on a set of fluency measures that are commonly used in an RTI model of classification and instruction. Six classification schemes were operationalized. Two Low-Achievement groups were formed based on their performance on oral reading fluency (ORF) or nonword fluency (NWF). Two Unexpected Low Achievement groups were also formed for both ORF and NWF by forming groups of students who performed below what would be expected based upon their vocabulary performance (which served as a proxy for verbal aptitude). A dual-discrepancy (Speece and Case, 2001) classification group was also identified. Finally, a sixth scheme was investigated based upon a relatively new classification scheme called a hybrid or constellation model (Fletcher et al., 2013; Wagner, 2008). These hybrid or constellation models recognize that all indicators of reading problems (cognitive, behavioral, or genetic) are imperfect indicators of a reading problem and contain error, and one possible way to mitigate this issue is by the use of multiple “signs” of reading problems. The constellation model is in many ways analogous to the practice of increasing the number of items on a test in order to make the overall score more reliable. In the Spencer et al. (2014) study, multiple constellation models were investigated based upon the number of times a student was identified using the previous 5 classification schemes. The findings from the Spencer et al. (2014) study replicated previous findings of low stability for the classification schemes that relied on single indicators or reading problems. For the constellation models, they found slightly larger stability as measured by kappa and substantially larger stability based upon estimates of consistency, which reflect the likelihood that a student will be classified as having a problem in the second year given that the student was identified in the first year.
Some of the inconsistency seen with all of these models may be due to the high probability that we are fitting categorical classification systems onto what is most likely a multidimensional and normally distributed construct with no distinct subgroups of people (Braunum-Martin, Fletcher, & Stuebing, 2013; Snowling and Hulme, 2012). However, even if it is the case that we are fitting categorical classification schemes onto a multidimensional construct – perhaps for the purposes of research or deciding levels of intervention – one would still expect a higher level of cross-categorical agreement and longitudinal stability. We have identified three potential reasons for the observed low agreements and longitudinal instability: Measurement error, regression to the mean, and true interindividual differences in change.
Assessing reading ability (or any psychological construct for that matter) requires the use of assessments and these all contain at least some amount of error. The particular items chosen to represent a construct, the testing particulars of that day, and the variability in the precision of the assessment across the range of ability can all produces errors in scores that are used to create these categories. Measurement errors in most assessments are also greater in magnitude the farther the score is from the mean as most reading assessments are designed to be more precise in the middle of the distribution (Francis et al., 2005). This imprecision in measurement results in students at the lower end of the distribution having a higher likelihood of fluctuating around a cut-point (Brown Waesche et al., 2011).
Directly related to measurement error is the phenomena known as regression to the mean (Rogosa, 1995; Furby, 1973). Conceptually, regression to the mean states that on average a score that is farther away from the mean on the first assessment will be closer to the mean on a second assessment, when the correlation between the first and second assessments is less than 1.0. Because all scores are measured with at least some error, a correlation between scores obtained at two time points will most likely to be less than 1.0. For this reason, regression to the mean has been thought to be unavoidable. The impact of regression to the mean on classifying children is that as the cut-point used becomes farther away from the mean, the more likely students in that group will have scores that are closer to the mean on a second assessment. As the cut-point moves toward the tails of the distribution, longitudinal instability will increase.
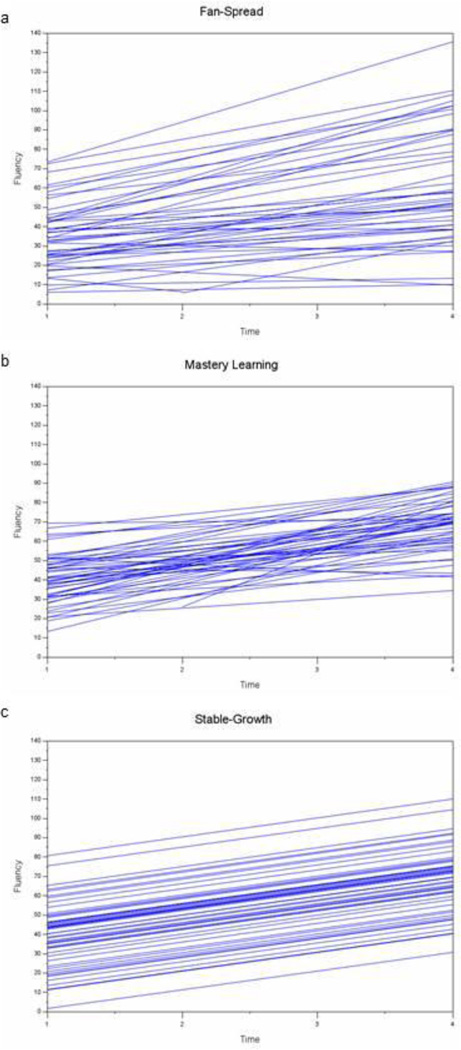
However, Rogosa (1995) points out that regression to the mean is not unavoidable. It is unavoidable only if the standard deviations of the scores at both time points are assumed to be equal. But if that assumption is relaxed, regression to the mean is avoidable. In fact, it is even possible to have “egression” from the mean (Rogosa, 1995; Nesselroade, Stigler, & Baltes, 1995). This could occur in a situation of fan-spread growth (Figure 1a). In a fan-spread growth pattern, observations that are below the mean change more slowly than observations that are above the mean. The result of this pattern of growth is a positive correlation between initial score and change, and increasing variance in scores over time. It is possible that this pattern of growth could provide more longitudinal stability in the classification schemes because fewer students would be growing out of the disability category. This pattern of growth has been referred to as a “Matthew Effect” in in reading research (Stanovich, 1986) and is thought to arise in the presence of reciprocal relations between reading skills and either vocabulary or reading motivation.
Figure 1.
The three patterns of growth investigated in this paper: (a) Fan-Spread Growth, (b) Mastery Learning, and (c) Stable-Growth.
The opposite pattern of growth is also possible. That is, a pattern of growth where students who are initially below average grow faster than above average students. This pattern is called a mastery learning pattern of growth (Venter, Maxwell, & Bolig, 2002; See Figure 1b). This pattern of growth could result in lower longitudinal stability as more kids in the lowest group are growing faster and may not be classified as disabled at the second measurement point. This pattern of change is the expected outcome when implementing a multi-tiered intervention where the lowest performing students received the most intensive instruction. Finally, it should be noted that regression to the mean can be operating in the presence of both forms of growth, where it exacerbates classification instability in the presence of mastery learning growth pattern and lowers the stability expected from a fan-spread growth pattern.
The third reason that longitudinal instability may exist is that students are truly changing categories. In the presence of a substantial amount of true inter-individual change in growth rates, it should be expected that students will correctly move in and out of these classifications. More generally, in the presence of substantial individual differences in growth, the actual meaning of longitudinal stability comes into question. In most classification studies, the presence of longitudinal stability is implicitly seen as a proxy for the ability to identify a trait that is stable and not prone to change. Therefore, longitudinal instability in a trait that thought to be stable is viewed as a problem with the classification scheme or measurement error. But if a large proportion of instability is due to true change, then using longitudinal stability as an index of classification validity no longer makes sense.
Three potential reasons for categorical and longitudinal instability have been posited: Measurement error and regression to the mean, true growth, and pattern of true growth. Investigating these factors in observed data would be difficult if not impossible to accomplish. The amount of measurement error, true growth, and pattern of change are all constants in an observed dataset and are not directly manipulable. However they are manipulable in a simulation study. Simulations have been successfully employed in reading research to address a number of issues. Francis et al., 2005 used simulations to investigate the impact of measurement error around a cut-point when classifying children with learning disability. Branum-Martin, Fletcher, & Stuebing, (2013) employed simulation techniques that explored the consequences of creating categories in the presence of co-morbid conditions and also the concordance of different classification schemes in identifying students using different cognitive discrepancy models (Stuebing, Fletcher, Branum-Martin, & Francis, 2012).
In all three of the previously mentioned simulation studies, the parameters used in the simulations were all based upon observed parameter estimates from existing datasets. In the present simulation, we also use an original dataset to obtain realistic population estimates. Data from the Spencer et al. (2014) were used to construct our simulation. This study differs from previous simulations by incorporating growth estimates across multiple domains thought to be related to reading in an attempt to more realistically capture overall level of reading-related abilities at a particular point in time and how they grow and influence each other over time. To obtain the most realistic estimates of growth and relations among different reading skills, we needed to fit a statistical model to the original data that would accomplish three things: Fit the observed data adequately, generate estimates of growth in multiple constructs, and allow for growth in one construct to impact growth in another other. To that end, we decided to fit a parallel process growth curve model (Preacher, Whichman, MacCallum, & Briggs, 2002). This model allows for the simultaneous estimation of growth in two or more constructs while allowing overall ability level and growth in each construct to influence overall level and growth in the others. We needed to be able to simultaneously estimate growth in two constructs (oral reading fluency and nonword fluency) to replicate and extend the work of Spencer et al., 2014. Although low NWF alone or unexpected low performance on NWF would most likely not ever be used to classify students as being reading impaired, it was necessary to classify students on their ability to read nonsense words as these classifications are a part of the proposed hybrid or constellation model (Spencer et al., 2012).
Estimates of overall ability, variation in growth, and relations among constructs were then used as population estimates for our simulation, and some of them were manipulated to provide different possible growth scenarios under which the performance of various classification schemes might be investigated. Specifically, three simulated datasets were constructed to investigate the roles of different patterns of change, measurement error and regression to the mean, and true individual differences in change on the accuracy of differing proposed classification schemes. In the first dataset, no parameters from the original model were manipulated. This model best represents the original dataset and the parameters of this model showed evidence of fan-spread growth In addition to this dataset, two more were created. In the second dataset, we set true growth to zero. That is, the simulated subjects in this dataset are exhibiting overall no true growth over time, although their overall levels of ability (intercepts) are allowed to vary (Figure 1c). The parameters of the third dataset are identical to the first in all respects except one: The correlation between intercept and slope was made to be the same size as in the first dataset but in the opposite direction. This will produce a modest mastery-learning pattern of growth.
Comparing the longitudinal classification stability of the fanspread-growth dataset to the mastery learning dataset will yield information about the impact of the form of growth, while comparing the result of the no- or stable-growth simulation to the other two growth datasets will inform us about the role of true-growth in classification scheme instability, since in the stable-growth dataset instability can only be due to measurement error and regression to the mean. If the classification results in the stable-growth dataset are similar to the other two datasets, it would imply that true change is not a large reason for longitudinal classification instability. We predict that the stable-growth dataset will produce more stable longitudinal classifications than the datasets that contain true individual differences in growth, and in the datasets that have some true variation in growth, we predict increased longitudinal classification stability when growth is in a fan-spread pattern than when growth is in a master-learning pattern. Finally, based upon previous simulation, we predict that as the cut-point chosen for identification moves away from the mean, the classification stability will decrease.
Method
Participants
The participants included a total of 31,339 first grade students who were in Florida schools for the 2003–2004 school-year, of whom 24,687 were followed to the end of second grade. Forty one percent of the students were White, 32% were Black, 21% were Hispanic, 4% reported mixed ethnicity and 1% where Asian/Pacific Islander. About 75% of the students were reportedly receiving free or reduced priced lunch benefits. These are the same students whose data were used in the Spencer et al. (2014) study. The data from this study were collected during the beginning years of The Reading First Initiative of the No Child Left Behind Act (2001) in Florida. In the summer before the 2003–2004 school year, teachers were required to attend a Reading First teacher training academy provided by the Florida Department of Education. This training was designed to help them practice and learn strategies for effective instruction in the areas of phonological awareness, decoding, vocabulary, and reading comprehension. Schools were also required to dedicate at least 90 minutes per day to reading instruction, and the curriculum used in the classroom had to be one of the 5 approved curricula from the state adoption list that was determined by state officials and research consultants to be aligned with evidence-based practices. At the time, RTI was not being used as a method for classifying students, but the results of the progress monitoring assessments were being used to create subgroups of students to differentiate instruction.
Measures
DIBELS Nonsense Word Fluency (NWF)
This measure requires the child to read vowel-consonant and consonant-vowel-consonant, single syllable pseudowords all of which have the short vowel sound. After a practice trial, the examiner instructs the child to read the “make believe” words as quickly and accurately as possible. If the child does not respond within 3 seconds, the examiner prompts with “next?” The stimuli are presented in 12 rows of five words each. Alternate-forms reliability is good (r =. 83 to .94; Speece, Mills et al., 2003) and predictive and concurrent criterion-related validity coefficients with reading (r =. 36 to .91; Speece, Mills et al., 2003) are adequate to good. There are 20 alternate forms. The original scoring guidelines give credit for correctly producing individual phonemes or for producing the pseudoword as a blended unit. Thus, if the nonsense word is “vab,” 3 points are awarded if the child says /v/ /a/ /b/ or “vab.” Three alternate forms were administered at each of 8 time points and the median number of words read correctly at each time point was used as their score for that time-point.
DIBELS Oral Reading Fluency (ORF)
This measure is a test of accuracy and fluency with connected text. The ORF passages are calibrated for the goal level of reading for each grade level. Student performance is measured by having students read a passage aloud for one minute. Words omitted, substituted, and hesitations of more than three seconds are scored as errors. Words self-corrected within three seconds are scored as accurate. The number of correct words per minute from the passage is the oral reading fluency rate. Speece and Case (2001) reported parallel forms reliability coefficient of .94 and predictive criterion-related validity coefficient of .78 (October to May) with the Basic Reading Skills Cluster score. These data correspond with other reports of strong technical adequacy of these measures (e.g., Deno, 1985). Three alternate forms were administered at each of 8 time point and the median number of words read correctly was their score.
Peabody Picture Vocabulary Test – III (PPVT). The PPVT – III is a measure of receptive vocabulary. Students are asked to point to one of four pictures that best matches a spoken vocabulary word. Split-half reliability of the PPVT-III is .93 (Dunn & Dunn, 1997).
Procedures
Students were assessed a total of 10 times over a two-year period for the data used in this study. The DIBELS assessments were administered four times in first grade (October, December, February, and April) and four times in second grade by a trained reading coach that had been assigned to each school. The PPVT-III was administered in the middle of each school year and was also administered by the same trained reading coach.
Data Analytic Plan
Model growth
The overall data analytic plan was to model growth in ORF and NWF and their relations with PPVT in order to obtain parameter estimates that would be used in a simulation of how these skills change and relate to each other over the two-year period. We chose to model growth in ORF and NWF using a piece-wise parallel process linear growth curve model. This model was chosen over other potential models primarily because of its ability to allow for the estimation of a different growth parameter for the first grade and second grade years respectively. We fit a two-rate model (Bryk and Raudenbush, 1992) that fit a single intercept (set at the beginning of the first grade, and two slope terms representing the linear rate of change in both first grade and second grade. This model was fit using a structural equation modeling framework and produced six latent variables: two intercept factors representing initial status in ORF and NWF, and four slope factors, representing the rates of change in ORF and NWF for first grade and second grade respectively. All six of these factors were allowed to correlate with each other as well as with the PPVT-III scores measured at both the middle of first and middle of second grade. Once this model was fit, estimates of the covariance among the six latent variables (and two manifest variables) along the latent means and variances and the residual variances from the 16 observed variables (8 ORF and 8 NWF) were used to construct our different simulations.
Simulations
Three different synthetic datasets containing 18 variables each were created using some or all of the parameters obtained from the original dataset. The first synthetic dataset, named the fan-spread dataset, was based completely on the intercept, slope, latent mean, and residual variance parameters obtained from the original dataset. The original piece-wise parallel linear growth curve model estimated fan spread growth for ORF and NWF in first grade, and smaller fan-spread growth for ORF and NWF in second grade. This dataset was constructed to examine how a simulated dataset would compare to an original dataset. The second dataset, the stable-growth dataset, was constructed from the parameters from the fan-spread model, with some differences. In this model, the latent slope means and variances for both ORF and NWF were set to zero. This implies that the students only differ from each other in their initial status in reading skill, and that at least at the population level, none of the students should change categories. The final dataset is called the mastery learning dataset. This dataset was constructed with the parameters from the fan-spread model, with one important distinction: The covariances between intercept and the slope terms for ORF and NWF were changed from positive to negative (with the magnitude of the covariance remaining unchanged).
All three of these datasets were constructed to have 31,000 students, which closely approximates the number of students in the original dataset. Finally, the simulated students in each of these datasets were identified as reading disabled or not reading disabled based upon the classification scheme described in the next section.
Classification schemes
The classification schemes used to classify students as reading disabled were closely based upon the operational definitions described in Spencer et al. (2014). Six classification schemes were operationalized. Low-Achievement was defined as low performance at the end of first and second grade for both ORF and NWF. These binary classifications were formed by creating z-scores of the observed simulated end-of-year ORF and NWF variables and using the standard normal distribution to identify three different cut-points that correspond to the 25th, 15th, or 5th percentiles. Unexpected Low Achievement for ORF and NWF was operationalized by regressing the end-of-year ORF and end-of year NWF scores onto PPVT scores (which served as a proxy for verbal aptitude) for first grade and second grade. The residuals from these four regressions were z-scored and three different cut-points were used to identify students who were below the 25th, 15th, or 5th percentiles. Dual Discrepancy was operationalized by fitting a hierarchical linear model (HLM) to ORF performance separately for first grade and second grade. The HLM centered the intercept at the end of the year, and allowed for a random intercept and random slope. The intercept and slope terms were both z-scored and students were identified as dual discrepant if both their intercept (predicted end of year performance) and slope (growth throughout the year) were below the 25th, 15th, or 5th percentiles. It should be noted that this operationalization was different than in Spencer et al. (2014), who created a composite of the intercept and slope scores and created classifications based upon that summed score. We decided to go with the dual discrepancy definition that most closely resembles the one employed in practice, even though it would yield different incidence rates than the other schemes. Finally, the Constellation Model was operationally defined as the presence of any one (or two) of the previous five possible classifications: Low Achievement on ORF or NWF, Unexpected Low Achievement on ORF or NWF, or Dual Discrepant.
Results
Descriptives
Means, standard deviations, and numbers of students taking each assessment are presented in Table 1. In general, there appears to be mean growth in both the ORF and NWF scores over time, as well as increasing variance in these scores over the 8 measurement time points. The PPVT-III standard scores indicate that the sample is performing slightly below the normative sample, but the standard deviations are close to the normative sample.
Table 1.
Means, Standard Deviations, and Maximum Likelihood Estimated Correlations.
| NWF1 | NWF2 | NWF3 | NWF4 | NWF5 | NWF6 | NWF7 | NWF8 | ORF1 | ORF2 | ORF3 | ORF4 | ORF5 | ORF6 | ORF7 | ORF8 | PPVT1 | PPVT2 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NWF1 | 1.00 | |||||||||||||||||
| NWF2 | .76 | 1.00 | ||||||||||||||||
| NWF3 | .71 | .78 | 1.00 | |||||||||||||||
| NWF4 | .65 | .72 | .79 | 1.00 | ||||||||||||||
| NWF5 | .63 | .68 | .75 | .78 | 1.00 | |||||||||||||
| NWF6 | .58 | .64 | .70 | .74 | .80 | 1.00 | ||||||||||||
| NWF7 | .56 | .62 | .69 | .73 | .77 | .81 | 1.00 | |||||||||||
| NWF8 | .53 | .58 | .65 | .70 | .73 | .77 | .82 | 1.00 | ||||||||||
| ORF1 | .73 | .66 | .63 | .57 | .55 | .50 | .49 | .46 | 1.00 | |||||||||
| ORF2 | .73 | .72 | .69 | .63 | .61 | .56 | .55 | .52 | .93 | 1.00 | ||||||||
| ORF3 | .73 | .73 | .76 | .71 | .68 | .64 | .63 | .61 | .85 | .91 | 1.00 | |||||||
| ORF4 | .70 | .71 | .74 | .74 | .71 | .67 | .67 | .65 | .76 | .83 | .93 | 1.00 | ||||||
| ORF5 | .68 | .69 | .73 | .72 | .75 | .69 | .69 | .67 | .71 | .79 | .89 | .93 | 1.00 | |||||
| ORF6 | .66 | .68 | .72 | .72 | .73 | .72 | .71 | .68 | .69 | .77 | .87 | .91 | .94 | 1.00 | ||||
| ORF7 | .64 | .66 | .70 | .70 | .72 | .69 | .73 | .70 | .63 | .71 | .82 | .88 | .92 | .93 | 1.00 | |||
| ORF8 | .61 | .64 | .68 | .68 | .70 | .67 | .69 | .70 | .59 | .67 | .78 | .86 | .90 | .90 | .95 | 1.00 | ||
| PPVT1 | .36 | .35 | .33 | .32 | .32 | .32 | .30 | .30 | .34 | .35 | .38 | .38 | .39 | .38 | .40 | .38 | 1.00 | |
| PPVT2 | .38 | .37 | .36 | .35 | .36 | .35 | .35 | .34 | .36 | .38 | .42 | .42 | .44 | .44 | .45 | .43 | .80 | 1.00 |
| Mean | 27.60 | 42.87 | 49.62 | 59.66 | 57.30 | 70.90 | 77.18 | 84.39 | 13.30 | 20.00 | 33.77 | 48.76 | 56.36 | 56.72 | 71.36 | 85.02 | 92.90 | 94.79 |
| SD | 20.42 | 23.44 | 26.77 | 30.88 | 30.21 | 35.43 | 37.74 | 40.56 | 18.77 | 22.36 | 27.77 | 32.37 | 32.71 | 31.93 | 35.41 | 37.69 | 14.73 | 14.47 |
| N | 31328 | 30070 | 29298 | 28925 | 25504 | 23815 | 24851 | 24670 | 31325 | 30069 | 29296 | 28922 | 25516 | 23828 | 24868 | 24687 | 28721 | 24417 |
Note: ORF = Oral Reading Fluency; NWF=Nonword Fluency; PPVT1=Peabody Picture Vocabulary Test administered in the middle of first grade; PPVT2=Peabody Picture Vocabulary Test administered in the middle of second grade; The numbers after the abbreviations represent time points with 1=October 1st grade, 2=December, 1st grade, 3=February, 1st grade, 4=April, 1st grade, 5=October, 2nd grade, 6=December, 2nd grade, 7=February, 2nd grade, 8=April, 2nd grade.
Growth Model for ORF and NWF
Mplus version 7.11 (Muthen & Muthen, 1998–2012) was used to fit a piecewise parallel linear growth curve model to estimate growth in both ORF and NWF over first grade and second grade. The intercept was centered at the first time period and the intercept and both slope terms were allowed to vary for both ORF and NWF. The variances, covariances, and correlations of the latent growth parameters, along with their latent means, are presented in Table 2. The positive correlations between ORF intercept – Grade 1 ORF slope (r=.33) and NWF intercept and NWF grade 1 slope (r=.23) indicate a small-to-moderate amount of fan-spread growth occurring in Grade 1 for both fluency variables. In second grade, however, the intercept-slope correlations are near zero for ORF (r=.10) and for NWF (r=.06). The latent slope means indicate that the students did improve on average over the course of the two years on these fluency tasks. The overall fit of this model was marginal (χ2= 35012.9, df=129, p<.0001; TLI=.90, RMSEA=.09). Further model testing indicated that the model fit was not improved by adding a quadratic growth term in either first grade or second grade for either ORF or NWF. Simulations and classifications. Using the Monte-Carlo facility in Mplus version 7.11 (Muthen & Muthen, 1998–2011) three synthetic datasets were created based upon the parameters estimated in the piecewise parallel growth model described previously, along with the error variances of the indicators. The Fan-spread dataset was simulated based upon all the parameters obtained from the original analysis, the stable-growth dataset used all the parameters from the original analysis, but set the slope means and slope variances to zero, and the mastery learning dataset used the original parameters but changed the relationship of the intercept and slopes from positive to negative. These simulations created 31,000 subjects with 8 NWF scores, 8 ORF scores, and 2 PPVT scores each. These data were then uploaded to SAS Version 9.4 to create the six different classifications described previously for the 25th, 15th, and 5th percentiles.
Table 2.
Variances, Covariances, and Latent Means from the Piecewise Parallel Growth Curve Model.
| Latent actors | ORF Int | Orf Slope G1 |
Orf Slope G2 |
NWF Int | NWF Slope G1 |
NWF Slope G2 |
PPVT G1 | PPVT G2 |
|---|---|---|---|---|---|---|---|---|
| ORF Int | 344.27 | .33 | .10 | .82 | .14 | .05 | .34 | .36 |
| Orf Slope G1 | 39.97 | 42.94 | −.56 | .50 | .66 | .23 | .31 | .36 |
| Orf Slope G2 | 7.94 | −15.47 | 17.92 | .00 | .16 | .54 | .12 | .16 |
| NWF Int | 281.05 | 60.51 | −0.33 | 338.50 | .23 | .06 | .40 | .42 |
| NWF Slope G1 | 14.60 | 23.55 | 3.79 | 22.93 | 29.65 | .24 | .11 | .18 |
| NWF Slope G2 | 4.88 | 7.77 | 12.08 | 6.04 | 6.90 | 27.60 | .12 | .15 |
| PPVT G1 | 92.31 | 29.68 | 7.52 | 107.49 | 11.74 | 9.04 | 217.74 | .65 |
| PPVT G2 | 97.92 | 33.72 | 9.56 | 111.52 | 14.54 | 11.53 | 170.80 | 210.05 |
| Latent Means | 29.07 | 9.71 | 6.01 | 12.79 | 10.70 | 8.98 | 92.73 | 94.61 |
Note: Correlations are above the diagonal, covariances are below the diagonal, and variances are on the diagonal. Int=Intercept which represents average level of performance at the beginning of first grade, ORF=Oral Reading Fluency, NWF=Nonword Fluency, PPVT=Peabody Picture Vocabulary Test, G1=First Grade, G2=Second Grade. Note: Correlations are above the diagonal, covariances are below the diagonal, and variances are on the diagonal. Int=Intercept which represents average level of performance at the beginning of first grade, ORF=Oral Reading Fluency, NWF=Nonword Fluency, PPVT=Peabody Picture Vocabulary Test, G1=First Grade, G2=Second Grade.
To describe and quantify the one year stability of the differing classification schemes, a number of indices were used and are reported in Tables 3 through 6. The incidents rates for reading disabilities for each classification scheme are reported for first and second grade. To the extent that the data are normally distributed, these incidence rates should reflect the percentile cut-offs used to create the groupings. Additionally, three indices of stability are reported. Kappa, which reports on the percent classification agreement between first grade and second grade, adjusted for chance agreement, the affected status agreement statistic (Brown Waesche et al, 2011) which represents the percentage of time a student is classified as reading disabled in both grades, conditioned upon whether they were identified as reading disabled in either grade, and consistency, which is the percentage of students who were identified as reading disabled in first grade that were also identified as reading disabled in second grade. It should be noted that consistency can also be called positive predictive power.
Table 3.
Incidence Rates, Kappa, ASA, and Consistency Values for Alternative Definitions of Reading Disabilities with Cut-Points at the 25th Percentile
| Incidence |
||||||
|---|---|---|---|---|---|---|
| Classification | Type of Growth | Grade 1 | Grade 2 | Kappa | ASA | Consistency |
| Low NWF | Stable-Growth | .25 | .25 | .37 | .36 | .53 |
| Low NWF | Mastery Learning | .25 | .25 | .35 | .34 | .51 |
| Low NWF | Fan-spread | .25 | .25 | .44 | .41 | .58 |
| Unexpected NWF | Stable-Growth | .25 | .25 | .31 | .32 | .48 |
| Unexpected NWF | Mastery Learning | .25 | .25 | .26 | .29 | .45 |
| Unexpected NWF | Fan-spread | .25 | .25 | .38 | .37 | .54 |
| Low ORF | Stable-Growth | .25 | .25 | .55 | .49 | .66 |
| Low ORF | Mastery Learning | .25 | .25 | .47 | .43 | .60 |
| Low ORF | Fan-spread | .25 | .25 | .58 | .52 | .69 |
| Unexpected ORF | Stable-Growth | .25 | .25 | .51 | .46 | .63 |
| Unexpected ORF | Mastery Learning | .25 | .25 | .33 | .33 | .49 |
| Unexpected ORF | Fan-spread | .25 | .25 | .50 | .46 | .62 |
| Dual Discrepancy | Stable-Growth | .24 | .24 | .78 | .72 | .86 |
| Dual Discrepancy | Mastery Learning | .14 | .14 | .33 | .28 | .47 |
| Dual Discrepancy | Fan-spread | .19 | .19 | .37 | .31 | .41 |
| ANY1PLUS | Stable-Growth | .50 | .50 | .60 | .67 | .81 |
| ANY1PLUS | Mastery Learning | .47 | .47 | .56 | .62 | .78 |
| ANY1PLUS | Fan-spread | .47 | .47 | .60 | .65 | .81 |
| ANY2PLUS | Stable-Growth | .28 | .28 | .72 | .67 | .80 |
| ANY2PLUS | Mastery Learning | .26 | .26 | .62 | .56 | .71 |
| ANY2PLUS | Fan-spread | .25 | .25 | .69 | .63 | .78 |
Note: ASA = Affected Status Agreement Statistic, NWF=Nonword Fluency, ORF=Oral Reading Fluency, ANYPLUS1=Has at least one or more of the five possible classifications of reading disabilities at both time points, ANYPLUS2=Has at least two or more of the five possible classifications of reading disabilities at both time points.
Table 3–5 contain the stability indices for the six classification schemes under three growth patterns for classifications based upon using the 25th, 15th, and 5th percentile cut-offs respectively. Table 6 contains the mean stability indices for type of growth collapsed over classification scheme and percentile cut-off, and classification scheme means collapsed over type of growth and percentile cut-offs. Overall, it appears from Table 6 that the classification schemes are the most stable in the presence of no (stable) growth (consistency=.59), followed by fan-spread growth (consistency=.53), and are the least stable in the presence of a mastery learning growth pattern (consistency=.46). In terms of which classification schemes are the most stable, it appears that the constellation model produces classifications that remain the most stable from first grade to second grade (consistency ranges from .70 to .68). Classifications were also more stable using the ORF measures than they were using the NWF measure. The unexpected low achievement classifications were less stable than their respective regular low achievement definitions for ORF and NWF, and were in fact the least stable classifications. But overall, the constellation model classification scheme produced considerably more stable classifications than the other schemes.
Table 5.
Incidence Rates, Kappa, ASA, and Consistency Values for Alternative Definitions of Reading Disabilities with Cut-Points at the 5th Percentile
| Incidence |
||||||
|---|---|---|---|---|---|---|
| Classification | Type of Growth | Grade 1 | Grade 2 | Kappa | ASA | Consistency |
| Low NWF | Stable-Growth | .05 | .05 | .26 | .17 | .29 |
| Low NWF | Mastery Learning | .05 | .05 | .24 | .16 | .27 |
| Low NWF | Fan-spread | .05 | .05 | .33 | .22 | .35 |
| Unexpected NWF | Stable-Growth | .05 | .05 | .22 | .15 | .25 |
| Unexpected NWF | Mastery Learning | .05 | .05 | .18 | .12 | .22 |
| Unexpected NWF | Fan-spread | .05 | .05 | .27 | .18 | .30 |
| Low ORF | Stable-Growth | .05 | .05 | .45 | .31 | .47 |
| Low ORF | Mastery Learning | .05 | .05 | .37 | .25 | .39 |
| Low ORF | Fan-spread | .05 | .05 | .49 | .35 | .52 |
| Unexpected ORF | Stable-Growth | .05 | .05 | .39 | .27 | .42 |
| Unexpected ORF | Mastery Learning | .05 | .05 | .22 | .15 | .25 |
| Unexpected ORF | Fan-spread | .05 | .05 | .40 | .28 | .43 |
| Dual Discrepancy | Stable-Growth | .05 | .05 | .73 | .59 | .76 |
| Dual Discrepancy | Mastery Learning | .02 | .02 | .17 | .10 | .21 |
| Dual Discrepancy | Fan-spread | .03 | .03 | .22 | .13 | .18 |
| ANY1PLUS | Stable-Growth | .13 | .13 | .56 | .45 | .64 |
| ANY1PLUS | Mastery Learning | .12 | .12 | .47 | .37 | .54 |
| ANY1PLUS | Fan-spread | .11 | .11 | .54 | .42 | .62 |
| ANY2PLUS | Stable-Growth | .05 | .05 | .67 | .52 | .67 |
| ANY2PLUS | Mastery Learning | .04 | .04 | .48 | .33 | .47 |
| ANY2PLUS | Fan-spread | .04 | .04 | .64 | .49 | .63 |
Note: ASA = Affected Status Agreement Statistic, NWF=Nonword Fluency, ORF=Oral Reading Fluency, ANYPLUS1=Has at least one or more of the five possible classifications of reading disabilities at both time points, ANYPLUS2=Has at least two or more of the five possible classifications of reading disabilities at both time points.
Table 6.
Kappa, ASA, and Consistency Estimate by Type of Growth and Classification Scheme
| Type of Growth | Kappa | ASA | Consistency |
|---|---|---|---|
| Fan-spread | .46 | .39 | .53 |
| Mastery Learning | .36 | .31 | .46 |
| Stable Growth | .51 | .44 | .59 |
| Classification Scheme | |||
| Low NWF | .33 | .28 | .42 |
| Unexpected NWF | .27 | .24 | .37 |
| Low ORF | .48 | .39 | .56 |
| Unexpected ORF | .39 | .32 | .48 |
| Dual Discrepancy | .43 | .35 | .48 |
| ANY1PLUS | .56 | .53 | .70 |
| ANY2PLUS | .64 | .53 | .68 |
Note: ASA = Affected Status Agreement Statistic, NWF=Nonword Fluency, ORF=Oral Reading Fluency, ANYPLUS1=Has at least one or more of the five possible classifications of reading disabilities at both time points, ANYPLUS2=Has at least two or more of the five possible classifications of reading disabilities at both time points.
But the collapsed information in Table 6 does not tell the whole story. Inspecting Tables 3–5 reveals that some new patterns emerge. First, all the classification schemes are more stable using the 25th percentile as the cut-off, and become increasing less stable as the percentile cut-off decreases. Second, it appears that the pattern of stability for the dual-discrepancy model does not follow the pattern of the rest of the classification schemes. Specifically, dual-discrepancy was the most stable in the stable-growth condition, and was considerably less stable in both the fan-spread growth condition and the mastery learning condition. For the rest of the classification schemes, it appears that for the most part, classification schemes were at their most stable in the presence of fan-spread growth, and were at their least stable in the presence of mastery learning. Fourth, it appears that as the cut-off percentile decreases, the difference in stability between fan-spread growth and mastery learning increased, with the classification schemes being much more stable in the presence of fan-spread growth as opposed to mastery learning growth. Finally, in comparing the two different versions of the constellation model, it appears that identifying students if one or more positive classification occurred on the five other schemes identified about twice as many students as the other schemes. However, using the classification scheme of having two or more other classifications at both first grade and second grade demonstrated incidence rates in line with the other schemes, and still had higher stability indices.
Discussion
Three datasets of synthetic observations were simulated that reflected three patterns of growth: stable-growth, fan-spread growth, and mastery-learning. Results from our simulation indicate that, in general, longitudinal stability was highest in the fan-spread condition and the lowest in the mastery learning condition. One notable exception to this finding occurred in for the dual-discrepancy classification, which was sizably more stable in the stable-growth condition than in either the mastery learning or fan-spread growth condition. Additionally, all classifications were less stable as the cut-score value was decreased. Finally, the rudimentary form of a constellation model classification scheme that included multiple criteria produced the most stable classifications, and the discrepancy models produced the least stable classifications.
The prediction that the stable-growth condition would produce the most stable classifications held for the dual-discrepancy classification, but did not hold for the others. By only allowing the initial level of reading ability to vary by student it implies that none of the students should change categories except due to measurement error and regression to the mean. It’s clear from the low stability indices for the stable-growth condition that measurement error and regression to the mean play a large role in longitudinal instability. Stability in the stable-growth condition was considerable higher for the dual-discrepancy definition, which uses direct estimates of growth and intercept in the definition. But with the average consistency of .59 for the stable-growth condition collapsed across classification scheme and cut-scores, it’s clear that in this simulation, true individual differences in growth is not playing a large role the longitudinal instability seen in these classifications.
The comparison of the fan-spread growth condition and mastery learning condition produced the expected pattern of higher stability in the fan-spread growth condition. Students that are identified as low performing at the beginning of the study who also grow more slowly are more likely to remain in the bottom percentiles of reading skill than if they were growing more quickly. This makes intuitive sense and this prediction was borne out in the simulation. More interestingly, however, was the finding that the classifications were more stable in the fan-spread condition as compared to the stable-growth condition. That is, even though there were true individual differences in growth trajectories in the fan-spread growth condition, it produced more stable classifications than the condition that had no reliable individual differences in growth. One possible explanation for this result is that the pattern of growth in the fan-spread condition worked to counter-act the effect of regression to the mean that is occurring in the stable-growth condition.
Finally, it appears that the rudimentary version of a constellation model produces the most stable classifications. This finding replicates and extends the findings from Spencer et al. (2014). Particularly interesting in this paper was the finding that the classification rule of at least two out of five “symptoms” had to present at both time points to be classified as disabled produced incidence rates that were directly in line with the specified cut-points and produced much higher stability rates than the other classification schemes that had the same incidence rates. We can only speculate as to why this classification scheme produced greater longitudinal stability. It’s possible that in the presence of measurement error and regression to the mean occurring, any classification scheme that is based upon one or two measured scores is likely to produce more identified children that “cross the threshold” and are no longer identified. Adding additional symptoms to the constellation model, and not requiring that any one single symptom be present, may make it less likely that, for example, two symptoms are present solely due to measurement error, and that they are also less likely to both cross the cut-score threshold.
There are limitations to this study. First, this study was based upon the dataset used in the Spencer et al. (2014) study that used quick-to-administer CBM measures that may contain a large amount of measurement error. However, Barth et al. (2008) reported similarly poor rates of agreement despite the use of more reliable measures. Relatedly, our study (along with Spencer et al, 2014) only used four assessments per grade to estimate growth in each grade. This may have produced a larger amount of unreliability in the estimation of growth in this study than would be experienced if more assessments per year were obtained. The smaller number of assessments would most likely impact the stability of the dual-discrepancy classification scheme the most. Secondly, our paper makes the assumption that oral reading fluency and nonword fluency are measuring the same construct to the same degree over the entire age range. If this assumption does not hold, it could also introduce longitudinal classification instability. Thirdly, our operationalization of RTI did not include any classroom observations or assurances that the students were receiving “high quality” tier 1 instruction. In this study, tier 1 was the presence of general education. Thirdly, our simulations were based upon the parameters obtained from the Spencer et al. (2014) dataset. It’s possible that more (or less) stable classification results may have been obtained if another sample was used to base our simulation. However, we do expect that the general findings about classification stability in the presence of different forms of growth to remain regardless of sample. Additionally, since this simulation is solely based upon the parameters obtained in the Spencer et al.,(2014) study, the results may not generalize to other samples or populations, especially where mastery growth may be present since mastery growth was not observed in the Spencer et al.,(2014) dataset and therefore its magnitude had to be estimated.
There are a couple of implications from the results of this study. First, the increased stability evidenced by the version of a constellation model implemented implies that researchers and practitioners alike should have more confidence that a child has a reading disability when multiple signs of its presence are present. Due to measurement error and the idiosyncrasies inherent in every assessment tool, it might not make sense to rely on any one particular assessment to diagnose a reading disability, or to maintain that a reading disability exists over time. The second implication stems from the result that true-interindividual differences in growth plays a minimal role in the large amount of observed classification instability seen in this study and most likely others. This implies that either (a) large amounts of error exist in our assessments of reading ability, (b) our models of reading disability are inadequate, or (c) perhaps both. Finally, we wanted to note that even though a constellation model that uses multiple sources of information proved to be the most stable, it does not necessarily imply that reading disorders are multi-dimensional. That is, it’s possible that a unitary or a multidimensional construct could produce a pattern of results similar to those seen in this paper.
In conclusion, this study provides further empirical support for the relative stability of hybrid or constellation models of reading (Wagner, 2008) in which multiple, theoretically coherent, sources of information are examined. An important next step is to develop and evaluate more sophisticated versions of constellation models. For example, it would be possible to combine multiple sources of information dimensionally by using a weighted average of indicators that predict the probability of the existence of a reading disability, thereby minimizing the effects of cut-points on continuous distributions. The results of this study also illuminate the conditions by which we should expect greater or lesser amounts of stability in classification. It also appears that the main driver of classification instability is measurement error and that true interindividual differences in growth play a much smaller role. A potentially important area for future research would be to conduct more simulation studies that identify just how much measurement precision is needed to obtain a satisfactory level of stability for different classification schemes, and to determine how much more effort is needed to develop those assessments.
Table 4.
Incidence Rates, Kappa, ASA, and Consistency Values for Alternative Definitions of Reading Disabilities with Cut-Points at the 15th Percentile
| Incidence |
||||||
|---|---|---|---|---|---|---|
| Classification | Type of Growth | Grade 1 | Grade 2 | Kappa | ASA | Consistency |
| Low NWF | Stable-Growth | .15 | .15 | .34 | .28 | .43 |
| Low NWF | Mastery Learning | .15 | .15 | .30 | .26 | .40 |
| Low NWF | Fan-spread | .15 | .15 | .40 | .33 | .49 |
| Unexpected NWF | Stable-Growth | .15 | .15 | .28 | .24 | .39 |
| Unexpected NWF | Mastery Learning | .15 | .15 | .23 | .21 | .34 |
| Unexpected NWF | Fan-spread | .15 | .15 | .35 | .28 | .44 |
| Low ORF | Stable-Growth | .15 | .15 | .53 | .43 | .59 |
| Low ORF | Mastery Learning | .15 | .15 | .44 | .35 | .53 |
| Low ORF | Fan-spread | .15 | .15 | .55 | .45 | .62 |
| Unexpected ORF | Stable-Growth | .15 | .15 | .47 | .38 | .55 |
| Unexpected ORF | Mastery Learning | .15 | .15 | .29 | .25 | .40 |
| Unexpected ORF | Fan-spread | .15 | .15 | .47 | .38 | .55 |
| Dual Discrepancy | Stable-Growth | .14 | .14 | .78 | .69 | .84 |
| Dual Discrepancy | Mastery Learning | .07 | .07 | .28 | .20 | .37 |
| Dual Discrepancy | Fan-spread | .10 | .10 | .31 | .23 | .30 |
| ANY1PLUS | Stable-Growth | .33 | .33 | .60 | .58 | .75 |
| ANY1PLUS | Mastery Learning | .31 | .31 | .54 | .52 | .70 |
| ANY1PLUS | Fan-spread | .30 | .30 | .59 | .56 | .74 |
| ANY2PLUS | Stable-Growth | .16 | .16 | .72 | .61 | .75 |
| ANY2PLUS | Mastery Learning | .14 | .14 | .58 | .47 | .63 |
| ANY2PLUS | Fan-spread | .14 | .14 | .68 | .57 | .72 |
Note: ASA = Affected Status Agreement Statistic, NWF=Nonword Fluency, ORF=Oral Reading Fluency, ANYPLUS1=Has at least one or more of the five possible classifications of reading disabilities at both time points, ANYPLUS2=Has at least two or more of the five possible classifications of reading disabilities at both time points.
References
- Barlow DH. Introduction to the special issue on diagnosis, dimensions, and DSM-IV: The science of classification. Journal of Abnormal Psychology. 1991;100:243–244. doi: 10.1037/h0092428. [DOI] [PubMed] [Google Scholar]
- Barth AE, Stuebing KK, Anthony JL, Denton C, Mathes PG, Fletcher JM, Francis DJ. Agreement among response to intervention criteria for identifying responder status. Learning and Individual Differences. 2008;18:296–307. doi: 10.1016/j.lindif.2008.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bateman BD. An educational view of a diagnostic approach to learning disabilities. In: Hellmuth J, editor. Learning disorders. Vol. 1. Seattle, WA: Special Child Publications; 1965. pp. 219–239. [Google Scholar]
- Bradley R, Danielson L, Hallahan DP, editors. Identification of learning disabilities: Research to practice. Mahwah, NJ: Lawrence Erlbaum Associates Publishers; 2002. [Google Scholar]
- Branum-Martin L, Fletcher JM, Stuebing KK. Classification and identification of reading and math disabilities: the special case of comorbidity. Journal of Learning Disabilities. 2013;46(6):490–499. doi: 10.1177/0022219412468767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown Waesche JS, Schatschneider C, Maner JK, Ahmed Y, Wagner RK. Examining agreement and longitudinal stability among traditional and RTI-based definitions of reading disability using the affected-status agreement statistic. Journal of Learning Disabilities. 2011;44(3):296–307. doi: 10.1177/0022219410392048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bryk AS, Raudenbush SW. Hierarchical linear models: Applications and data analysis methods. Newbury Park, CA: Sage; 1992. [Google Scholar]
- Deno SL. Curriculum-based measurement. The emerging alternative. Exceptional Children. 1985;52:219–232. doi: 10.1177/001440298505200303. [DOI] [PubMed] [Google Scholar]
- Dunn LM, Dunn DM. Peabody Picture Vocabulary Test-Third Edition. Circle Pines, MN: AGS Publishing; 1997. [Google Scholar]
- Fletcher JM, Lyon GR, Fuchs LS, Barnes MA. Learning disabiliries: From identification to intervention. New York, NY: Guilford Press; 2007. [Google Scholar]
- Fletcher JM, Steubing KK, Morris RD, Lyon GR. Classification and identification of learning disabilities: A hybrid model. In: Swanson HL, Harris K, editors. Handbook of learning disabilities. 2nd. New York: Guilford Press; 2013. pp. 33–50. [Google Scholar]
- Francis DJ, Fletcher JM, Stuebing KK, Lyon GR, Shaywitz BA, Shaywitz SE. Psychometric Approaches to the Identification of LD: IQ and Achievement Scores Are Not Sufficient. Journal of Learning Disabilities. 2005;38(2):98–108. doi: 10.1177/00222194050380020101. [DOI] [PubMed] [Google Scholar]
- Fuchs D, Fuchs LS. Introduction to response to intervention: What, why, and how valid is it? Reading Research Quarterly. 2006;41:93–99. [Google Scholar]
- Furby L. Intrpresting regression toward the mean in developmental research. Developmental Psychology. 1973;8:172–179. [Google Scholar]
- Good RH, Simmons DC, Kame’enui EJ. The importance and decision-making utility of a continuum of fluency-based indicators of foundational reading skills for third grade high-stakes outcomes. Scientific Studies of Reading. 2001;5:257–288. [Google Scholar]
- Muthen L, Muthen B. Mplus Users Guide. 7th. Los Angeles, CA: Muthen & Muthen; 1998–2012. [Google Scholar]
- Nesselroade JR, Stigler SM, Baltes PB. Regression toward the mean and the study of change. Psychological Bulletin. 1980;88:622–637. [Google Scholar]
- Rogosa D. Myths and methods: “Myths about longitudinal research” plus supplemental questions. In: Gottman JM, editor. The Analysis of Change. LEA: Mahway, NJ; 1995. pp. 3–66. [Google Scholar]
- Schatschneider C. I am ROC curves (and so can you)! In: Petscher Y, Schatschneider C, Compton D, editors. Applied Quantitative Analysis in Education and the Social Sciences. New York, NY: Routledge; 2013. pp. 65–92. [Google Scholar]
- Snowling MJ, Hulme C. Annual research review: The nature and classification of reading disorders: A commentary on the proposals for the DSM-5. Journal of Child Psychiatry and Psychology. 2012;53:593–607. doi: 10.1111/j.1469-7610.2011.02495.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Speece DL, Case LP. Classification in context: An Alternative approach to identifying early reading disability. Journal of Educational Psychology. 2001;93:735–749. [Google Scholar]
- Speece DL, Mills C, Ritchey KD, Hillman E. Initial Evidence That Letter Fluency Tasks Are Valid Indicators of Early Reading Skill. The Journal of Special Education. 2003;36(4):223–233. [Google Scholar]
- Spencer M, Wagner RK, Schatschneider C, Quinn JM, Lopez D, Petscher Y. Incorporating RTI in a Hybrid Model of Reading Disability. Learning Disability Quarterly. 2014;37:161–171. doi: 10.1177/0731948714530967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stuebing KK, Fletcher JM, Branum-Martin L, Francis DJ. Evaluation of the Technical Adequacy of Three Methods for Identifying Specific Learning Disabilities Based on Cognitive Discrepancies. School Psychology Review. 2012;41:3–22. [PMC free article] [PubMed] [Google Scholar]
- Venter A, Maxwell SE, Bolig E. Power in randomized group comparisons: The value of adding a single intermediate time point to a traditional pretest-posttest design. Psychological Methods. 2002;7(2):194–209. doi: 10.1037/1082-989x.7.2.194. [DOI] [PubMed] [Google Scholar]
- Wagner RK. Rediscovering dyslexia: New approaches for identification and classification. In: Reid G, Fawcett A, Manis F, Seigel L, editors. The Handbook of Dyslexia. Thousand Oaks, CA: Sage; 2008. pp. 174–191. [Google Scholar]