Figure 1.

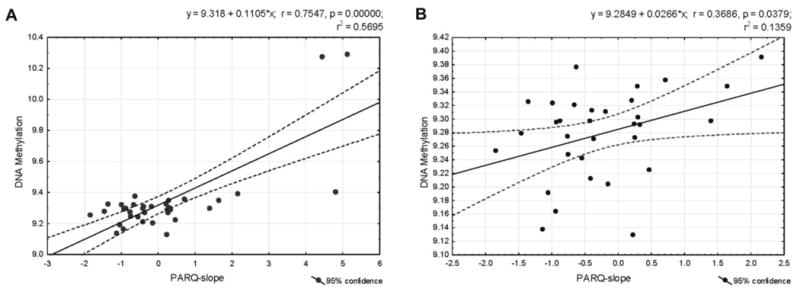
Linear regression model that relates the score of dynamic change in perceived parental rejection (PARQ-slope) and the mean methylation levels of 818 parenting-associated markers, or 300bp MBD-seq fragments for the entire sample of 35 individuals (A) and for 32 samples, with the exclusion of extreme cases (B). Figure 1A shows that the sample contains three extreme cases. One case had an unusually high PARQ-slope value (4.82) with average DNA methylation compared to the rest of the sample (i.e., exerting a leverage on the regression line). Two cases showed discrepancies as reflected in high PARQ-slope values (5.12 and 4.45) and high DNA methylation. A set of diagnostic analyses of the regression of mean methylation on PARQ-slope values and the covariates was performed to identify any concerns with these extreme cases. Results showed (1) no concerning leverage of mean methylation on the fitted values as indicated by hat values (values were 0.48, 0.46, and 0.46; mean hat value was 0.17); (2) no unusual large or small residuals as indicated by most studentized residuals within the ± 2 range (largest studentized residual was 2.64 with a Bonferroni-adjusted p-value of .47); (3) no major influence on the regression coefficients of PARQ-slope as indicated by a plot of residuals against leverage (Cook's d values were 0.87, 0.54, and 0.84). Given the small sample size, we have tested and evaluated other types of robust regression models using high breakdown point (M- or MM-) estimators as these models tend to be less vulnerable to unusual data. Estimators such as “least trimmed squares” and “least median of squares” are alternatives to ordinary least squares regression that account better for the effect of extreme values. However, these methods led to problems of convergence in many of the regression models we tested. In robust regression using M-estimators, Wald-type inference of the significance of coefficients typically requires larger samples—due to the unreliable asymptotic covariance matrix in small samples—than the data available in this study. Thus, although we were aware of the potential influence of these cases on the regression, we decided to utilize ordinary least squares regression but cautiously interpret the results. Figure 1B shows that the association between the PARQ-slope and the mean of ME-markers is high and significant within the sample after removing the three extreme cases. The y-axis (mean DNA-methylation) has been rescaled to better illustrate the linear interrelation.