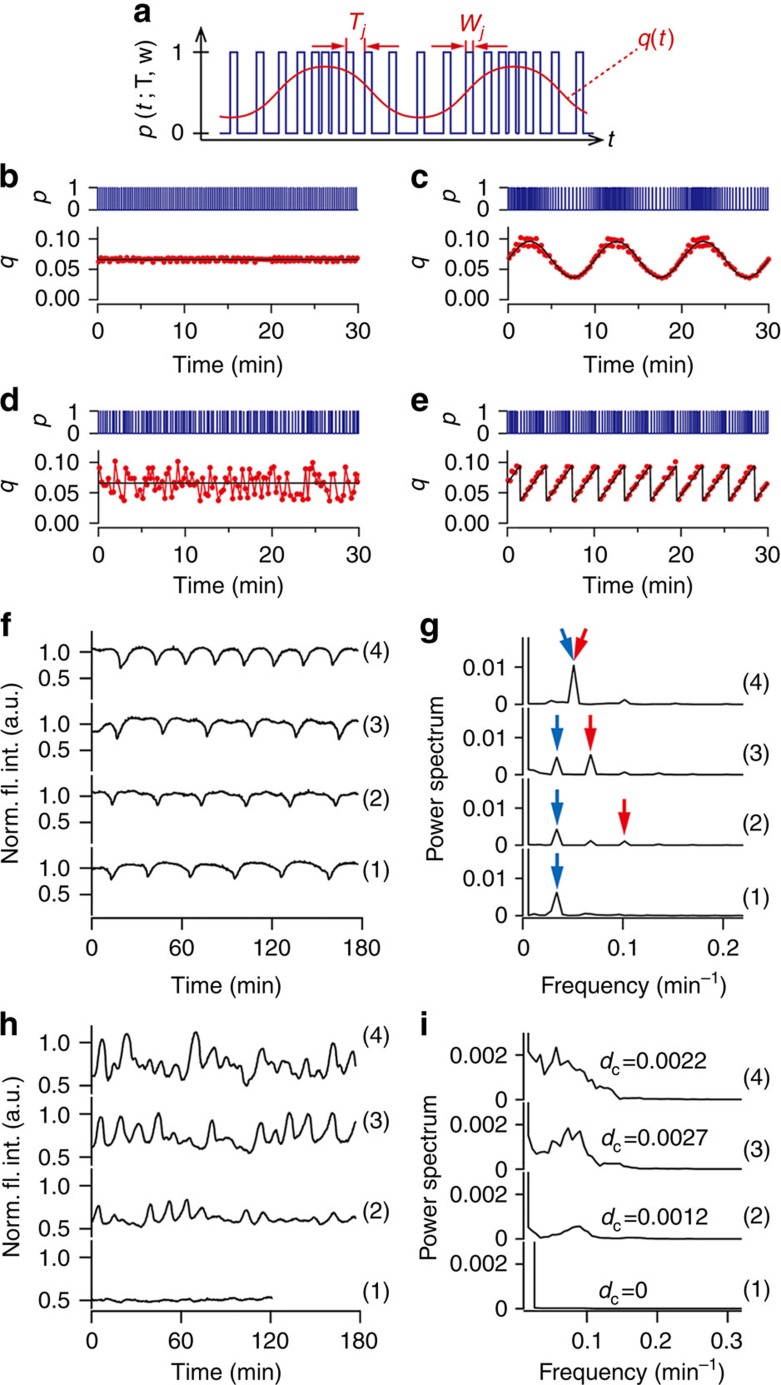
Figure 4. Time-variable external control of chemical oscillation dynamics using the droplet open-reactor system.

(a) Schematic diagram of the pulse-density modulation control of time-variable q(t). When the pulse train of p(t; T, w) is denser, q(t) is higher, and vice versa. (b–e) Generation of p and q. Blue lines: pulse trains of p(t; T, w); black lines: (b,c,e) theoretical curves of q(t) and (d) theoretical average of q(t); red dots and lines: q(t) generated in experiments, calculated as q(t=τ_j)=w_j/T_j. w_j=0.99 s (fixed for all j). (b) Constant (Z_C(t)). (c) Sinusoidal wave (Z_S(t), A_q=0.45, T_q=10 min). (d) White noise (Z_N(t), A_q=0.45). (e) Saw-tooth wave functions (Z_St(t), A_q=0.45, T_q=3 min). Z_C(t), Z_S(t), Z_N(t) and Z_St(t) are described in detail in the Methods section. The baseline value of q(t): 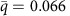. (f) Entrainment of the chemical oscillation to the external sinusoidal signal. 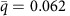. (1) A_q=0 (without sinusoidal signal) and (2–4) A_q=0.45. (2) T_q=10 min, (3) T_q=15 min and (4) T_q=20 min. (g) Power spectra of f. (h) Noise-induced pulsed excitation when white noise was added to SSL. 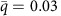. (1) A_q=0 (without noise), (2) A_q=0.15, (3) A_q=0.3 and (4) A_q=0.45. (i) Power spectra of h. 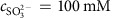. The compositions of the solutions in the transporter and reactor are given in the Methods section. Norm. fl. int., normalized fluorescence intensity.