Abstract
The indentation test is widely used to determine the in situ biomechanical properties of articular cartilage. The mechanical parameters estimated from the test depend on the constitutive model adopted to analyze the data. Similar to most connective tissues, the solid matrix of cartilage displays different mechanical properties under tension and compression, termed tension-compression nonlinearity (TCN). In this study, cartilage was modeled as a porous elastic material with either a conewise linear elastic matrix with cubic symmetry or a solid matrix reinforced by a continuous fiber distribution. Both models are commonly used to describe the TCN of cartilage. The roles of each mechanical property in determining the indentation response of cartilage were identified by finite element simulation. Under constant loading, the equilibrium deformation of cartilage is mainly dependent on the compressive modulus, while the initial transient creep behavior is largely regulated by the tensile stiffness. More importantly, altering the permeability does not change the shape of the indentation creep curves, but introduces a parallel shift along the horizontal direction on a logarithmic time scale. Based on these findings, a highly efficient curve-fitting algorithm was designed, which can uniquely determine the three major mechanical properties of cartilage (compressive modulus, tensile modulus, and permeability) from a single indentation test. The new technique was tested on adult bovine knee cartilage and compared with results from the classic biphasic linear elastic curve-fitting program.
Keywords: Biphasic, Fiber-reinforced, Curve-fitting, Creep, Optimization
Introduction
Indentation testing is a commonly-used technique to determine the mechanical properties of articular cartilage, as it is site-specific, non-destructive, and suitable for testing of small joints with a limited amount of tissue.5, 7, 31 To obtain mechanical properties from indentation data, a specific constitutive model has to be employed to describe the cartilage mechanical behavior, and the model response curve-fitted to the data. Due to the complexity of the boundary conditions, theoretical indentation solutions can be difficult to develop, especially for comprehensive constitutive models.25 When cartilage is treated as linear elastic material, the Hertzian contact solution on an infinite half space is widely used, which is specifically suitable for nano- or micro-indentation tests.24 For larger-scale indenters, Hayes solution17 is often used since it removes the infinite half-space assumption in the Hertzian contact problem. In the early 1980's, Mow and coworkers32 developed a porous elastic model for articular cartilage. An indentation solution was also developed based on the theory.28 Using this theoretical solution, a curve-fitting algorithm was established that can simultaneously determine the Young's modulus, shear modulus, and permeability of the cartilage from a single indentation creep curve.30 Besides these closed-form solutions, many other linear, numerical solutions for cartilage indentation have been developed to account for the variety of experimental parameters, such as the geometry of the indenter tip and the loading profile.2, 6, 14, 16, 38 All of these linear solutions have been widely-used to extract the biomechanical properties of cartilage from indentation tests.4, 6, 9, 22, 26, 36
However, the mechanical behavior of the cartilage's solid matrix itself is nonlinear and strain-dependent due to the nature of the collagen networks and trapped proteoglycans. In particular, the tensile modulus of cartilage is found to be an order of magnitude higher than the compressive modulus.8, 19 A few TCN constitutive models have been proposed to account for this, including a conewise linear elastic (CLE) model with cubic symmetry and several fibril reinforced models.13, 37, 43 Simulations based on these models show that the prominent nonlinearity in the stress-strain relationship of the solid matrix regulates the flow-dependent viscosity and is therefore an essential characteristic of the transient mechanical behavior.34, 43 A few recent studies have analyzed indentation or nano-indentation tests using these nonlinear constitutive models.15, 29, 39 However, since these nonlinear models typically contain multiple parameters, determination of all the relevant cartilage properties by curve-fitting a single indentation curve is often complicated by over-fitting, local minima, and multiple solutions.20 For instance, to avoid local minima, multiple optimizations are often performed with different initial guess of the tissue properties. However, little knowledge is available about the different roles of each individual mechanical properties in shaping the creep behavior of cartilage, or whether these features can benefit or accelerate the curve-fitting algorithm. Indeed, no strategies are currently available that can uniquely determine the tensile and compressive properties of cartilage based on a single indentation test.
In this study, a highly efficient technique was developed to determine the nonlinear biphasic properties of cartilage from a single indentation creep test. First, the roles of the three key individual properties (compressive modulus E, permeability k, and fiber modulus ξ) in the indentation response of cartilage were analyzed and identified. Second, an optimization algorithm was designed based on these findings, which can simultaneously and uniquely determine the three properties by fitting a single indentation curve. This new algorithm was then applied to analyze experimental data from adult bovine knee cartilage. The results were validated by comparison with the classical biphasic linear elastic program.
Materials and Methods
1. Indentation Test
Seventeen cartilage-bone blocks, with intact cartilage surface, were harvested from the trochlear groove of two skeletally mature (18 months old) bovine knee joints, in a region where the articular surface has relatively small curvature. Indentation testing was performed as described previously.5, 26 In brief, samples were submerged in PBS supplemented with protease inhibitors and tested on an indentation device equipped with a rigid, porous, flat-ended cylindrical indenter tip (ϕ = 2.1 mm). A 20 mN tare load was first applied for 0.5 h to ensure full contact between the indenter and cartilage surface. Then a 200 mN step load was applied and maintained for another 2 h or until the creep deformation reached equilibrium. The cartilage thickness at the testing spot was later measured using the needle penetration method.30
2. Simulation with Nonlinear Constitutive Models
In the numerical simulations, the cartilage is modeled as a biphasic material with a tension-compression nonlinear solid matrix, which is treated as a compressible isotropic neo-Hookean ground matrix reinforced with fibers. The fibers can only sustain tensile stress, therefore the compressive modulus of the material is defined to be the Young's modulus of the neo-Hookean background at small strain.43 The permeability is also a property of the neo-Hookean solid matrix. When the fibers are organized in three orthogonal directions, this constitutive model displays mechanical behaviors similar to a CLE material with cubic symmetry and henceforth is referred to as the CLE model. Based on earlier experimental results,8 the strain energy density function of the fiber bundles is defined as3
| (1) |
and the Cauchy stress of the fiber is given by
| (2) |
| (3) |
| (4) |
In these equations, N is the unit vector in the fiber direction, C is the right Cauchy-Green deformation tensor, λn is the stretch ratio, F is the deformation gradient, J is the Jacobian of the deformation, and H is a Heaviside function used to ensure zero resistance of the fibers under compression. The parameter ξ is nonlinearly correlated with the fiber stiffness, and is referred to as the fiber modulus in this model. Constants α and β are set to 0 and 2 to render an almost linear stress-strain relationship at small strains,3 in which case the tissue tensile modulus Ef in the fiber direction can be written as
| (5) |
Alternatively, a number of studies assume the fibers are continuously distributed, known as a continuous fiber distribution (CFD) model. In this case, the strain energy density function of the fibers is still given by Eq. 1, while the Cauchy stress is integrated over all possible fiber directions.3
| (6) |
| (7) |
Here, φ and θ are the spherical angles of the fiber orientation in the local coordinate system.
In this study, the hydraulic permeability of the cartilage is assumed to be constant, homogeneous, and isotropic. Poisson's ratio of the neo-Hookean ground matrix is assumed to be 0 as suggested in the literature.8, 37 Two 3D FE models for the indentation creep test were built in FEBio 2.0,27 based on the biphasic CLE and CFD models respectively. Taking advantage of the axisymmetric nature of the indentation test, a 1° wedge of the cartilage and indenter (modeled as rigid) was analyzed with symmetry boundary conditions applied on the circumferential faces. The other boundary conditions are defined to be consistent with the actual experimental conditions (Fig 1). The FE mesh was biased in order to capture the rapid variation of the strain field and fluid pressure near the cartilage-indenter interface. A mesh convergence study was performed and the resulting mesh contained 2627 nodes and 1250 elements, including 1225 HEX8 type and 25 PENTA6 type elements. In the FE simulation, a constant force is applied on the indenter as a Heaviside function, and the displacement of indenter tip is calculated to generate the creep deformation curve. The results of the FE program serve as the basis for the curve-fitting technique to determine the mechanical properties from the indentation experiments.
Fig. 1.
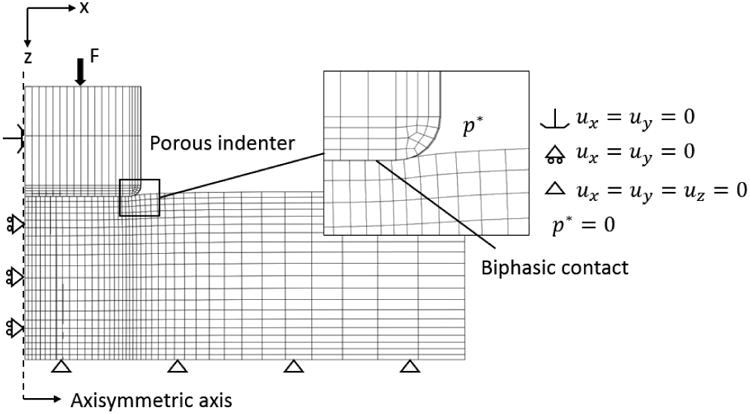
A one-degree wedge of cartilage and indenter is meshed and analyzed based on the axial symmetric nature of indentation tests. The bottom of the cartilage is impermeable and fixed in all directions to mimic the cartilage-bone interface. Deformation of the contact surface is associated with the movement of the indenter tip, and the fluid pressure is set to be zero (porous indenter). Ux,y,z represents the displacement in x, y, and z directions, respectively, and P is the fluid pressure.
3. Optimization Algorithm
As an initial step toward developing the curve-fit algorithm, the FE models were used to perform parametric studies to identify the effect of individual mechanical properties on the indentation creep deformation. Each of the three key parameters (compressive modulus E, permeability k, and fiber modulus ξ) was varied within the physiological range while keeping the other two constant. Results based on the biphasic CLE model are plotted over time on a logarithmic scale in Fig 3. The CFD model displayed the same trends (results not shown). The compressive modulus E has a significant effect on the equilibrium deformation (Fig 3a), while the fiber modulus mainly regulates the transient deformation in the early portion of the curve (Fig 3c). Varying the permeability does not change the overall slope of the curve or the equilibrium deformation, but shifts the deformation curve along the time axis (Fig 3b).
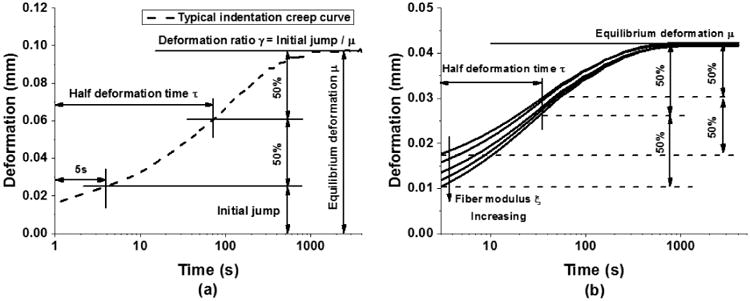
Fig. 3.
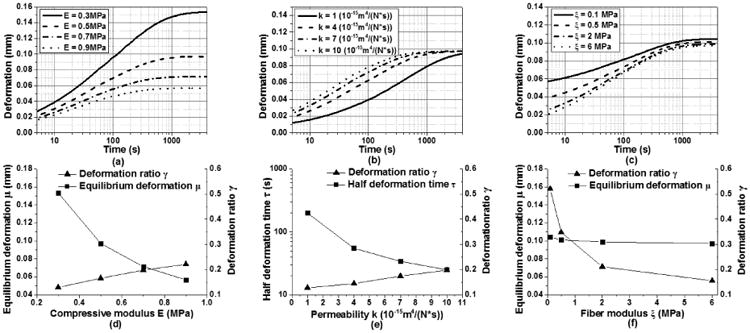
(a) A typical indentation creep curve from tests on bovine knee cartilage and the definition of three curve-related parameters, including the initial jump, equilibrium deformation, and half deformation time. (b) When the equilibrium deformation and half deformation time are fixed, the initial jump of the curve is regulated by the fiber modulus
In light of these observations, three defining characteristics of the creep curve are identified (Fig 2a): the equilibrium deformation μ, the deformation ratio γ, and the half deformation time τ. Equilibrium deformation μ is the deformation at steady state. The deformation ratio γ represents the ratio between the initial jump and equilibrium deformation, where the initial jump equals the indenter displacement at 5 s after the onset of loading. Half deformation time τ is the time at which the deformation reaches the halfway point between the initial jump and equilibrium deformation, and is an indication of the tissue viscosity. The correlations between these parameters (i.e., μ, γ, and τ) and the three mechanical properties (i.e., E, k, ξ) were calculated and plotted in Fig 3d-f. Both the fiber modulus and compressive modulus are negatively correlated with the tissue equilibrium deformation, and they have opposite effects on the deformation ratio (Fig 3d, f). The permeability is positively correlated with the deformation ratio and negatively correlated with the half deformation time (Fig 3e).
Fig. 2.
Roles of each individual mechanical property in shaping the indentation creep curve in biphasic CLE model. Creep curves are plotted by varying one of the three properties in the physiological range and keeping the other two constants. (a) compressive modulus, (b) permeability, and (c) fiber modulus. (d-f) Monotonic correlations between the mechanical properties and the deformation ratio, half deformation time, or equilibrium deformation of the creep curves.
In order to determine the individual mechanical properties (E, k, and ξ) from a single indentation experiment, the FE prediction is curve-fitted to the experimental creep curve. First, a fiber modulus ξ at the middle of the search range, which is set to be 0-5 MPa for CLE model and 0-2 MPa for CFD model based previous studies,3, 41 is selected as the starting value. The equilibrium deformation μ is a function of both the compressive modulus E and fiber modulus ξ, but not the permeability k. When ξ is fixed, μ decreases monotonically with increasing E (Fig 3d),
| (8) |
Therefore, a value for E corresponding to the assumed ξ can quickly be determined using a binary search based on μ. Next, a similar process is used to find the appropriate value of k corresponding to the assumed value of ξ According to Fig 3e, an increase in the permeability k shifts the creep curve to the left with no effect on the equilibrium deformation,
| (9) |
Thus k can also be determined using a binary search based on the half deformation time τ.
What remains is to check the accuracy of the assumed magnitude of ξ which can be done by considering the remaining parameter of the creep curve, the deformation ratio γ. With fixed values of E and k, variations in ξ significantly change the initial jump (Fig 3 c), which in turn affects the deformation ratio γ. When and τ are fixed, ξ is found to be monotonically related to the deformation ratio γ (Fig 2b). Thus another binary search can be used to find the value of ξ corresponding the experimental determined μ and τ,
| (10) |
This updated value of ξ is then used as the new starting value, and the entire process is repeated. The overall curve-fitting strategy is a two-level embedded binary search as illustrated in Fig 4. At the lower level, the compressive modulus and permeability are searched sequentially to match the equilibrium deformation and half deformation time for an assumed fiber modulus ξ. At the higher level, ξ is optimized to match the deformation ratio of the creep curve. Since the calculation of the equilibrium deformation is merely a static mechanics problem with no time dependent integration, the computational cost of this step is negligible. Moreover, all three parameters are determined using a binary search algorithm. The running time of the algorithm is O(log2n), where n is the number of partitions in the search range. Therefore, the optimization strategy runs efficiently and avoids the possible optimization complications of multiple solutions and local minima.
Fig. 4.
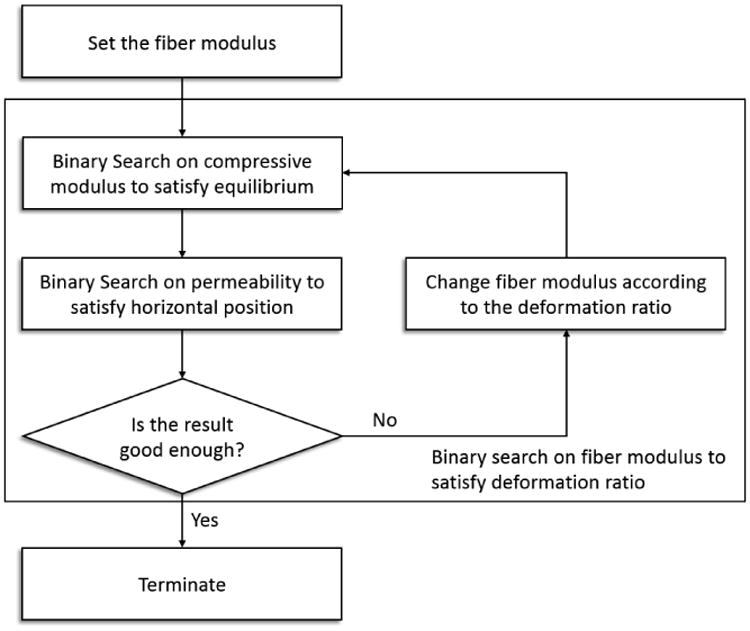
The optimization scheme involves two levels of binary search. At the lower level, given a fiber modulus, the compressive modulus and permeability are optimized to fit the equilibrium deformation and half deformation time of the curve. At the higher level, the fiber modulus is searched to match the deformation ratio. Adjustment of fiber modulus requires a new search of compressive modulus and permeability.
The optimization program is implemented in MATLAB 2013a (The MathWorks Inc.), where indentation creep simulations are handled by calling the FEBio program for each iteration. The error tolerance in the optimization was chosen as 0.5%. The creep data from the indentation tests on bovine cartilage have been analyzed using both CLE and CFD models, and the accuracy of the fit is measured by
| (11) |
where fi and yi are the ith simulation and ith experimental data point, respectively, and ȳ is the mean of y. The corresponding mechanical properties in the CLE and CFD models are correlated using a linear regression test, and they were also compared with those given by the classic curve-fitting program based on the BLE model.5, 30 The aggregate moduli, which is defined as the modulus under confined compression (=λ+2μ, λ and μ are Lame constants), and permeability from the three models were compared by one-way ANOVA with Tukey's post hoc test (p<0.05) on repeated measures.
Results
Two typical experimental indentation creep curves fitted by the optimization technique using both biphasic CLE and CFD models, as well as the classical BLE curve fitting program, are shown in Fig 5a. The CLE and CFD models generate nearly overlapping curves that match the experiments well over the entire time domain. The BLE fits the equilibrium deformation accurately, but not the short-term transient response since it is based on the elastic Hayes solution. In the actual experiment, immediately after the step loading, the cartilage behaves like an incompressible material, due to the interstitial fluid pressurization.34 Thus the compressive deformation in the loading direction has to be associated with tissue expansion in the radial direction. However, the relatively high tensile stiffness of the tissue provides resistance to this radial expansion, which in turn constrains the initial axial deformation. The high tensile stiffness featured in the CLE and CFD models allows these models to capture this short-term response and significantly improves the curve-fitting accuracy by reducing the initial jump. The average R-squared value of the fitted curves is 0.988±0.014 for the CLE model, 0.988±0.013 for the CFD model, and 0.781±0.082 for the BLE model. To determine the three mechanical properties using an experimental creep curve, ∼600 seconds computing time is required on a personal computer (Intel i5 3rd generation processor, 4 cores @ 3.4 GHz, and 16 GB memory). A typical optimization process is plotted in Fig 5b, which shows that four iterations may be enough to obtain a satisfactory fit to the fiber modulus ξ. For each creep curve, ∼36 iterations are required during the optimization to obtain the mechanical properties in the biphasic CLE model. In contrast, optimization using the Nelder-Mead simplex method takes 100-300 iterations to determine a set of mechanical properties, and the success of the optimization is dependent on the initial guess of properties.
Fig. 5.

(a) Typical indentation creep displacement history of adult bovine knee cartilage and the curve-fittings based on BLE and biphasic CLE and CFD models. (b) Typical searching process for fiber modulus ξ. The dashed lines are simulated curves over different ξ values after fixing equilibrium deformation and half deformation time.
The mechanical properties determined from the curve-fits using the three different constitutive models are listed in Table 1. The aggregate moduli were 0.438±0.253 MPa, 0.415±0.248 MPa, and 0.451±0.228 MPa for the CLE, CFD, and BLE models, respectively. One-way ANOVA shows that all three models differ from each other and the BLE model generates the highest compressive modulus, which is expected as the BLE model lumps the effect of the high tensile stiffness into the aggregate modulus and therefore increases the calculated value of the compressive modulus. The compressive moduli from the two nonlinear models are linearly correlated with each other, with a correlation coefficient R of 0.99 (Fig 6a). The slope of the linear fit is 1.02, and the offset is 0.01 MPa. The aggregate moduli from both nonlinear models are highly correlated with those from the BLE model (r > 0.99) (Fig 7a).
Table 1.
Mechanical properties determined by BLE, CLE, and CFD models.
| CFD model | CLE model | BLE model | |
| Aggregate modulus (MPa) | 0.415 ± 0.248 | 0.438 ±0.253* | 0.451 ± 0.228*+ |
| Fiber modulus (MPa) | 0.288 ± 0.209 | 1.519 ± 1.099* | / |
| Permeability (10−15m4/(N * s)) | 5.041 ± 2.154 | 5.597 ± 3.559 | 4.626 ± 2.322+ |
| R-squared | 0.988 ± 0.014 | 0.988 ± 0.013 | 0.781 ± 0.082*+ |
: different from CFD;
: different from CLE.
Fig. 6.
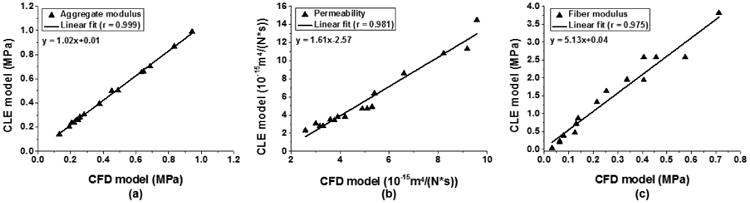
Correlations between mechanical properties determined by biphasic CLE and CFD models. (a) aggregate modulus, (b) permeability, and (c) fiber modulus.
Fig. 7.
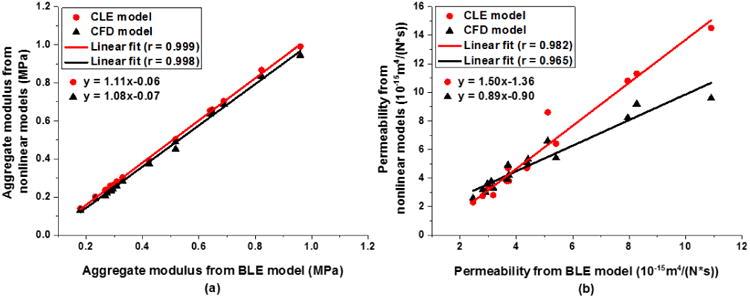
(a) Aggregate modulus and (b) permeability obtained from CLE and CFD models are linearly correlated with those from the BLE model.
The permeability determined from the curve-fits is 5.597±3.559×10-15 m4/(Ns), 5.041±2.154×10-15 m4/(Ns) and 4.626±2.322×10-15 m4/(Ns) for the CLE, CFD and BLE models, respectively. A significant difference is only detected between the CLE and BLE models (p = 0.007). Similar to the aggregate moduli, the permeability values from the three models are highly correlated with each other in a linear relationship (r > 0.96) (Fig 6b, 7b). As the fiber moduli in the two nonlinear models have different physical meanings, their magnitudes are not comparable with each other, but nevertheless they are linearly correlated (r = 0.98) (Fig. 6c).
To evaluate the effect of different Poisson's ratios on the outcome of our curve-fitting program, a parametric study was performed by varying the Poisson's ratio from 0 to 0.45 (Fig 8). Over this range, the R-squared value of the curve-fitting varies from 0.996 to 0.998, indicating that the assigned magnitude of Poisson's ratio has little effect on the goodness of curve-fit. When the Poisson's ratio is varied from 0 to 0.15, the calculated permeability and fiber modulus change 5% and 7%, respectively, and the aggregate modulus increases by 1%.
Fig. 8.

Curve-fitting is performed with different Poisson's ratios on a single creep curve, and its effect on the determined mechanical properties is plotted. All the mechanical properties are normalized by their maximum value.
Discussion
In the present study, the uniqueness of the curve-fit is a result of the distinct role that each of the three mechanical properties plays in shaping the simulated creep curve. The monotonic correlations between the curve characteristics and the mechanical properties shown in the parametric studies (Figs 2 and 3) contribute to this uniqueness and improve the efficiency of optimization. An essential observation that makes this curve-fitting technique viable is that variation in the permeability only shifts the half deformation time of the simulated creep curve along the logarithmic time scale. The same phenomenon has been noted previously and served as an important constraint in the indentation curve-fitting program based on the BLE model.30 Our current study shows that this useful phenomenon is retained when tension-compression nonlinearity is incorporated into the constitutive law. Moreover, the permeability values determined from the curve-fitting based on the BLE and CFD models (Table 1) displayed no statistical difference, which implies that the permeability in linear and nonlinear models may play similar, if not identical, roles in controlling the cartilage response under indentation.
The compressive moduli from the two nonlinear models are highly correlated with the modulus from the classic BLE model (r > 0.998), which helps confirm the accuracy of the FE program and the curve-fitting strategy. The determined mechanical properties of the bovine trochlear groove cartilage are consistent with other experimental measurements as well,42 which showed the aggregate modulus and the permeability to be 0.37±0.02 MPa and ∼10-15 m4/(Ns) respectively. In addition, the aggregate moduli from the CLE and CFD models are linearly correlated to each other with a slope close to 1, which confirms that the compressive modulus in the two nonlinear models are comparable with each other.
It should be noted that the tensile parameters in the two models have very different physical meanings. The fiber modulus ξ is correlated nonlinearly with the tensile modulus of the cartilage measured in the experiments, which itself is strain-dependent.3, 44 According to the correlation in Eq. 5, the CLE model gives an approximate tensile modulus of 6 MPa in this study, which is consistent with the physiological range of adult bovine knee cartilage.37, 41 However, the tensile modulus of the superficial tangential zone in cartilage has been shown to be approximately 2 times higher than that in the middle-deep zone.19 Since the deformation field in cartilage under large-scale indentation is heterogeneous, with higher tensile strains in the superficial layer, the tensile property determined by indentation could be affected more by the superficial tangential zone rather than the deep zone cartilage. The fiber modulus ξ in the CFD model has an implicit correlation with the engineering tensile modulus. Due to the continuous angular distribution of fibers, unidirectional tension will induce different levels of stretching among the fibers oriented in different directions. Therefore, the fiber modulus ξ has drastically different physical meaning in two models, and should only be compared directly with the values obtained from the same model as indicated previously.3 For healthy hyaline cartilage, the CFD model has been shown to explain the observed tissue behaviors, especially the strain-dependent Poisson's ratio, better than the CLE model.3 Consequently, the CLE model is more suited for some fibrous cartilage tissues with collagen fibers uniformly aligned in one or two directions, such as meniscus,23 the superficial zone of cartilage 35 and some fibrous cartilage.1, 11
The effective compressive Poisson's ratio of cartilage, measured directly by optical techniques,8, 12, 21, 40 is inherently small for a tension-compression nonlinear material, because the high tensile modulus confines the expansion of the tissue in the lateral direction. Since the tensile modulus is nonlinearly strain-dependent, the measured Poisson's ratio demonstrates a similar trend.3, 8 Poisson's ratio is higher at small compressive strains and sharply decreases to a value close to zero (∼0.03) as the compressive strain becomes higher than 4%.8 The Poisson's ratio used in both the CLE and CFD models, however, is assigned to the non-fibril ground matrix. Therefore the value chosen should be slightly higher than the tissue's effective Poisson's ratio.44 As there is no existing measurement of this parameter, it has been assumed to be somewhere between 0 and 0.15 in literature.29, 37, 44 Since Poisson's ratio decreases significantly from the deep zone to the superficial zone of cartilage 40 and the indentation response of cartilage is primarily regulated by the top layer, its value was fixed at 0 for this study.
A number of limitations in this study should be noted. First, the two nonlinear constitutive models employed are based on the continuum assumption, i.e., the basic assumption of porous elastic theory, which assumes there is a mixture of solid and fluid phases in any infinitesimal small volume. Since commercial nano-indenters recently became readily available, nano-indentation has been widely used for the characterization of cartilage.16, 24, 33 When the indenter size is on the same scale as collagen fibrils or chondrocytes,10 the continuum assumption is no longer valid, and the technique developed here is therefore not suitable for estimation of mechanical properties at the nano-scale. Secondly, articular cartilage has a much more complicated structure than that described by the two nonlinear models here. For example, the collagen fibers are organized heterogeneously across the cartilage, mainly aligned in the horizontal directions in the superficial zone and vertically in the deep zone. The hydraulic permeability is anisotropic and nonlinearly dependent on the dilatation of the solid matrix. In addition, the osmotic pressure induced by negatively charged proteoglycans contributes to the compressive stiffness. None of these is accounted for in the two tension-compression nonlinear models. Therefore, although the two current models can describe the overall transient mechanical behaviors of cartilage better than the linear isotropic theory, they represent simplifications of the real structure of the tissue. To quantify the predictive capability of the two nonlinear models, an initial analysis has been performed to verify whether the properties obtained from the curve-fitting can be used to predict the indentation response at a different level of load. The detailed methods and results are presented in the supplementary information. A thorough investigation of the predictive capability of the two constitutive models under various testing profiles represents an important future direction of this study. Furthermore, the intrinsic viscosity of solid matrix, which is a key factor regulating the short-term response of cartilage,18 is not considered in the two constitutive models. As the contribution of the intrinsic viscosity is lumped into the elastic properties of solid matrix, the tensile moduli determined using the CLE and CFD models may be an overestimation of the actual values. Thirdly, the tensile modulus in the nonlinear model can significantly affect the initial deformation or “jump” of the creep curve. To be consistent, we defined this “jump” at a specific time after the step loading. A parametric study showed that any time in the range of 1-15 seconds gave identical curve-fitting results. This selection disappears if a ramp loading is employed, in which case the initial jump can be defined as the deformation at the end of the loading phase.
In summary, a highly-efficient curve-fitting technique was developed which can uniquely and simultaneously determine the tensile modulus, compressive modulus and permeability of cartilage based on a single indentation test. Moreover, in light of the finite element analysis, the new curve-fitting program was built to be applied for various experimental profiles. For example, the loading profile could be step loading, ramp loading or some other loading function. In addition, the type of indenter tip, porous or impermeable, is also an adjustable parameter. The curve-fitting program will be available for free download in the FEBio forum and on our laboratory website.
Supplementary Material
Acknowledgments
DOD W81XWH-13-1-0148, Musculoskeletal Transplant Foundation, and NIH U54-GM104941. We also want to acknowledge the free, open-source FEBio software.
Footnotes
Conflict of Interest Statement: All authors state that they have no conflicts of interest.
References
- 1.Allen KD, Athanasiou KA. Viscoelastic characterization of the porcine temporomandibular joint disc under unconfined compression. J Biomech. 2006;39:312. doi: 10.1016/j.jbiomech.2004.11.012. [DOI] [PubMed] [Google Scholar]
- 2.Appleyard RC, Ghosh P, Swain MV. Biomechanical, histological and immunohistological studies of patellar cartilage in an ovine model of osteoarthritis induced by lateral meniscectomy. Osteoarthritis Cartilage. 1999;7:281. doi: 10.1053/joca.1998.0202. [DOI] [PubMed] [Google Scholar]
- 3.Ateshian GA, Rajan V, Chahine NO, Cana CE, Hung CT. Modeling the matrix of articular cartilage using a continuous fiber angular distribution predicts many observed phenomena. J Biomech Eng. 2009;131:061003. doi: 10.1115/1.3118773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Athanasiou KA, Agarwal A, Dzida FJ. Comparative study of the intrinsic mechanical properties of the human acetabular and femoral head cartilage. J Orthop Res. 1994;12:340. doi: 10.1002/jor.1100120306. [DOI] [PubMed] [Google Scholar]
- 5.Athanasiou KA, Rosenwasser MP, Buckwalter JA, Malinin TI, Mow VC. Interspecies comparisons of in situ intrinsic mechanical properties of distal femoral cartilage. J Orthop Res. 1991;9:330. doi: 10.1002/jor.1100090304. [DOI] [PubMed] [Google Scholar]
- 6.Bae WC, Lewis CW, Levenston ME, Sah RL. Indentation testing of human articular cartilage: effects of probe tip geometry and indentation depth on intra-tissue strain. J Biomech. 2006;39:1039. doi: 10.1016/j.jbiomech.2005.02.018. [DOI] [PubMed] [Google Scholar]
- 7.Bae WC, Temple MM, Amiel D, Coutts RD, Niederauer GG, Sah RL. Indentation testing of human cartilage: sensitivity to articular surface degeneration. Arthritis Rheum. 2003;48:3382. doi: 10.1002/art.11347. [DOI] [PubMed] [Google Scholar]
- 8.Chahine NO, Wang CC, Hung CT, Ateshian GA. Anisotropic strain-dependent material properties of bovine articular cartilage in the transitional range from tension to compression. J Biomech. 2004;37:1251. doi: 10.1016/j.jbiomech.2003.12.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chen X, Zimmerman BK, Lu XL. Determine the equilibrium mechanical properties of articular cartilage from the short-term indentation response. J Biomech. 2015;48:176. doi: 10.1016/j.jbiomech.2014.10.036. [DOI] [PubMed] [Google Scholar]
- 10.Darling EM, Zauscher S, Guilak F. Viscoelastic properties of zonal articular chondrocytes measured by atomic force microscopy. Osteoarthritis Cartilage. 2006;14:571. doi: 10.1016/j.joca.2005.12.003. [DOI] [PubMed] [Google Scholar]
- 11.Detamore MS, Athanasiou KA. Tensile properties of the porcine temporomandibular joint disc. J Biomech Eng. 2003;125:558. doi: 10.1115/1.1589778. [DOI] [PubMed] [Google Scholar]
- 12.DiSilvestro MR, Zhu Q, Wong M, Jurvelin JS, Suh JK. Biphasic poroviscoelastic simulation of the unconfined compression of articular cartilage: I--Simultaneous prediction of reaction force and lateral displacement. J Biomech Eng. 2001;123:191. doi: 10.1115/1.1351890. [DOI] [PubMed] [Google Scholar]
- 13.Fortin M, Soulhat J, Shirazi-Adl A, Hunziker EB, Buschmann MD. Unconfined compression of articular cartilage: nonlinear behavior and comparison with a fibril-reinforced biphasic model. J Biomech Eng. 2000;122:189. doi: 10.1115/1.429641. [DOI] [PubMed] [Google Scholar]
- 14.Guo H, Spilker RL. An augmented Lagrangian finite element formulation for 3D contact of biphasic tissues. Comput Methods Biomech Biomed Engin. 2014;17:1206. doi: 10.1080/10255842.2012.739166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gupta S, Lin J, Ashby P, Pruitt L. A fiber reinforced poroelastic model of nanoindentation of porcine costal cartilage: a combined experimental and finite element approach. J Mech Behav Biomed Mater. 2009;2:326. doi: 10.1016/j.jmbbm.2008.09.003. [DOI] [PubMed] [Google Scholar]
- 16.Han L, Frank EH, Greene JJ, Lee HY, Hung HH, Grodzinsky AJ, Ortiz C. Time-dependent nanomechanics of cartilage. Biophys J. 2011;100:1846. doi: 10.1016/j.bpj.2011.02.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hayes WC, Keer LM, Herrmann G, Mockros LF. A mathematical analysis for indentation tests of articular cartilage. J Biomech. 1972;5:541. doi: 10.1016/0021-9290(72)90010-3. [DOI] [PubMed] [Google Scholar]
- 18.Huang CY, Soltz MA, Kopacz M, Mow VC, Ateshian GA. Experimental verification of the roles of intrinsic matrix viscoelasticity and tension-compression nonlinearity in the biphasic response of cartilage. J Biomech Eng. 2003;125:84. doi: 10.1115/1.1531656. [DOI] [PubMed] [Google Scholar]
- 19.Huang CY, Stankiewicz A, Ateshian GA, Mow VC. Anisotropy, inhomogeneity, and tension-compression nonlinearity of human glenohumeral cartilage in finite deformation. J Biomech. 2005;38:799. doi: 10.1016/j.jbiomech.2004.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Julkunen P, Wilson W, Isaksson H, Jurvelin JS, Herzog W, Korhonen RK. A review of the combination of experimental measurements and fibril-reinforced modeling for investigation of articular cartilage and chondrocyte response to loading. Comput Math Methods Med. 2013;2013:326150. doi: 10.1155/2013/326150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Jurvelin JS, Buschmann MD, Hunziker EB. Optical and mechanical determination of Poisson's ratio of adult bovine humeral articular cartilage. J Biomech. 1997;30:235. doi: 10.1016/s0021-9290(96)00133-9. [DOI] [PubMed] [Google Scholar]
- 22.Le NA, Fleming BC. Measuring fixed charge density of goat articular cartilage using indentation methods and biochemical analysis. J Biomech. 2008;41:715. doi: 10.1016/j.jbiomech.2007.09.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.LeRoux MA, Setton LA. Experimental and biphasic FEM determinations of the material properties and hydraulic permeability of the meniscus in tension. J Biomech Eng. 2002;124:315. doi: 10.1115/1.1468868. [DOI] [PubMed] [Google Scholar]
- 24.Li Q, Doyran B, Gamer LW, Lu XL, Qin L, Ortiz C, Grodzinsky AJ, Rosen V, Han L. Biomechanical properties of murine meniscus surface via AFM-based nanoindentation. J Biomech. 2015;48:1364. doi: 10.1016/j.jbiomech.2015.02.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lu XL, Mow VC. Biomechanics of articular cartilage and determination of material properties. Med Sci Sports Exerc. 2008;40:193. doi: 10.1249/mss.0b013e31815cb1fc. [DOI] [PubMed] [Google Scholar]
- 26.Lu XL, Sun DD, Guo XE, Chen FH, Lai WM, Mow VC. Indentation determined mechanoelectrochemical properties and fixed charge density of articular cartilage. Ann Biomed Eng. 2004;32:370. doi: 10.1023/b:abme.0000017534.06921.24. [DOI] [PubMed] [Google Scholar]
- 27.Maas SA, Ellis BJ, Ateshian GA, Weiss JA. FEBio: finite elements for biomechanics. J Biomech Eng. 2012;134:011005. doi: 10.1115/1.4005694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Mak AF, Lai WM, Mow VC. Biphasic indentation of articular cartilage--I. Theoretical analysis. J Biomech. 1987;20:703. doi: 10.1016/0021-9290(87)90036-4. [DOI] [PubMed] [Google Scholar]
- 29.Makela JT, Huttu MR, Korhonen RK. Structure-function relationships in osteoarthritic human hip joint articular cartilage. Osteoarthritis Cartilage. 2012;20:1268. doi: 10.1016/j.joca.2012.07.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Mow VC, Gibbs MC, Lai WM, Zhu WB, Athanasiou KA. Biphasic indentation of articular cartilage--II. A numerical algorithm and an experimental study. J Biomech. 1989;22:853. doi: 10.1016/0021-9290(89)90069-9. [DOI] [PubMed] [Google Scholar]
- 31.Mow VC, Gu WY, Chen FH. Structure and function of articular cartilage and meniscus. In: Mow VC, Huiskes R, editors. Basic orthopaedic biomechanics and mechano-biology. Philadelphia: Lippincott Williams & Wilkins; 2005. pp. 181–258. [Google Scholar]
- 32.Mow VC, Kuei SC, Lai WM, Armstrong CG. Biphasic creep and stress relaxation of articular cartilage in compression? Theory and experiments. J Biomech Eng. 1980;102:73. doi: 10.1115/1.3138202. [DOI] [PubMed] [Google Scholar]
- 33.Moyer JT, Abraham AC, Haut Donahue TL. Nanoindentation of human meniscal surfaces. J Biomech. 2012;45:2230. doi: 10.1016/j.jbiomech.2012.06.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Park S, Krishnan R, Nicoll SB, Ateshian GA. Cartilage interstitial fluid load support in unconfined compression. J Biomech. 2003;36:1785. doi: 10.1016/s0021-9290(03)00231-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ruggiero L, Zimmerman BK, Park M, Han L, Wang L, Burris DL, Lu XL. Roles of the Fibrous Superficial Zone in the Mechanical Behavior of TMJ Condylar Cartilage. Ann Biomed Eng. 2015 doi: 10.1007/s10439-015-1320-9. [DOI] [PubMed] [Google Scholar]
- 36.Simha NK, Jin H, Hall ML, Chiravarambath S, Lewis JL. Effect of indenter size on elastic modulus of cartilage measured by indentation. J Biomech Eng. 2007;129:767. doi: 10.1115/1.2768110. [DOI] [PubMed] [Google Scholar]
- 37.Soltz MA, Ateshian GA. A conewise linear elasticity mixture model for the analysis of tension-compression nonlinearity in articular cartilage. J Biomech Eng. 2000;122:576. doi: 10.1115/1.1324669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Spilker RL, Suh JK, Mow VC. A finite element analysis of the indentation stress-relaxation response of linear biphasic articular cartilage. J Biomech Eng. 1992;114:191. doi: 10.1115/1.2891371. [DOI] [PubMed] [Google Scholar]
- 39.Taffetani M, Griebel M, Gastaldi D, Klisch SM, Vena P. Poroviscoelastic finite element model including continuous fiber distribution for the simulation of nanoindentation tests on articular cartilage. J Mech Behav Biomed Mater. 2014;32:17. doi: 10.1016/j.jmbbm.2013.12.003. [DOI] [PubMed] [Google Scholar]
- 40.Wang CC, Deng JM, Ateshian GA, Hung CT. An automated approach for direct measurement of two-dimensional strain distributions within articular cartilage under unconfined compression. J Biomech Eng. 2002;124:557. doi: 10.1115/1.1503795. [DOI] [PubMed] [Google Scholar]
- 41.Williamson AK, Chen AC, Masuda K, Thonar EJ, Sah RL. Tensile mechanical properties of bovine articular cartilage: variations with growth and relationships to collagen network components. J Orthop Res. 2003;21:872. doi: 10.1016/S0736-0266(03)00030-5. [DOI] [PubMed] [Google Scholar]
- 42.Williamson AK, Chen AC, Sah RL. Compressive properties and function-composition relationships of developing bovine articular cartilage. J Orthop Res. 2001;19:1113. doi: 10.1016/S0736-0266(01)00052-3. [DOI] [PubMed] [Google Scholar]
- 43.Wilson W, van Donkelaar CC, van Rietbergen B, Huiskes R. A fibril-reinforced poroviscoelastic swelling model for articular cartilage. J Biomech. 2005;38:1195. doi: 10.1016/j.jbiomech.2004.07.003. [DOI] [PubMed] [Google Scholar]
- 44.Wilson W, van Donkelaar CC, van Rietbergen B, Ito K, Huiskes R. Stresses in the local collagen network of articular cartilage: a poroviscoelastic fibril-reinforced finite element study. J Biomech. 2004;37:357. doi: 10.1016/s0021-9290(03)00267-7. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


