Private algorithms for the protected in social network search

Significance

Motivated by tensions between data privacy for individual citizens, and societal priorities such as counterterrorism, we introduce a computational model that distinguishes between parties for whom privacy is explicitly protected, and those for whom it is not (the “targeted” subpopulation). Within this framework, we provide provably privacy-preserving algorithms for targeted search in social networks. We validate the utility of our algorithms with extensive computational experiments on two large-scale social network datasets.

Abstract

Motivated by tensions between data privacy for individual citizens and societal priorities such as counterterrorism and the containment of infectious disease, we introduce a computational model that distinguishes between parties for whom privacy is explicitly protected, and those for whom it is not (the targeted subpopulation). The goal is the development of algorithms that can effectively identify and take action upon members of the targeted subpopulation in a way that minimally compromises the privacy of the protected, while simultaneously limiting the expense of distinguishing members of the two groups via costly mechanisms such as surveillance, background checks, or medical testing. Within this framework, we provide provably privacy-preserving algorithms for targeted search in social networks. These algorithms are natural variants of common graph search methods, and ensure privacy for the protected by the careful injection of noise in the prioritization of potential targets. We validate the utility of our algorithms with extensive computational experiments on two large-scale social network datasets.

The tension between the useful or essential gathering and analysis of data about citizens and the privacy rights of those citizens is at an historical peak. Perhaps the most striking and controversial recent example is the revelation that US intelligence agencies systemically engage in “bulk collection” of civilian “metadata” detailing telephonic and other types of communication and activities, with the alleged purpose of monitoring and thwarting terrorist activity (1). Other compelling examples abound, including in medicine (patient privacy vs. preventing epidemics), marketing (consumer privacy vs. targeted advertising), and many other domains.

Debates about (and models for) data privacy often have an “all or nothing” flavor: privacy guarantees are either provided to every member of a population, or else privacy is deemed to be a failure. This dichotomy is only appropriate if all members of the population have an equal right to, or demand for, privacy. Few would argue that actual terrorists should have such rights, which leads to difficult questions about the balance between protecting the rights of ordinary citizens, and using all available means to prevent terrorism. [A recent National Academies study (2) reached the conclusion that there are not (yet) technological alternatives to bulk collection and analysis of civilian metadata, in the sense that such data are essential in current counterterrorism practices.] A major question is whether and when individual privacy should be sacrificed in service of such societal priorities. Similarly, in the medical domain, epidemics (such as the recent international outbreak of Ebola; ref. 3) have raised serious debate about the clear public interest in controlling contagion versus the privacy rights of the infected and those that care for them.

The model and results in this paper represent a step toward explicit acknowledgments of such trade-offs, and algorithmic methods for their management. The scenarios sketched above can be broadly modeled by a population divided into two types. There is a protected subpopulation that enjoys (either by law, policy, or choice) certain privacy guarantees. For instance, in the examples above, these protected individuals might be nonterrorists, or uninfected citizens (and perhaps informants and health care professionals). They are to be contrasted with the “unprotected” or targeted subpopulation, which does not share those privacy assurances. A key assumption of the model we will introduce is that the protected or targeted status of individual subjects is not known, but can be discovered by (possibly costly) measures, such as surveillance or background investigations (in the case of terrorism) or medical tests (in the case of disease). Our overarching goal is to allow parties such as intelligence or medical agencies to identify and take appropriate actions on the targeted subpopulation, while also providing privacy assurances for the protected individuals who are not the specific targets of such efforts, all while limiting the cost and extent of the background investigations needed.

As a concrete example of the issues we are concerned with, consider the problem of using social network data (for example, telephone calls, emails, and text messages between individuals) to search for candidate terrorists. One natural and broad approach would be to use common graph search methods: beginning from known terrorist “seed” vertices in the network, neighboring vertices are investigated, in an attempt to grow the known subnetwork of targets. This general practice is sometimes referred to as contact chaining (section 3.1 of ref. 2). A major concern is that such search methods will inevitably encounter protected citizens, and that even taking action against only discovered targeted individuals may compromise the privacy of the protected.

To rigorously study the trade-offs between privacy and societal interests discussed above, our work introduces a formal model for privacy of network data that provides provable assurances only to the protected subpopulation, and gives algorithms that allow effective investigation of the targeted population. These algorithms are deliberately “noisy” and are privacy-preserving versions of the widely used graph search methods mentioned above, and as such represent only mild, but important, departures from commonly used approaches. At the highest level, one can think of our algorithms as outputting a list of confirmed targeted individuals discovered in the network, for whom any subsequent action (e.g., publication in a most-wanted list, further surveillance, or arrest in the case of terrorism; medical treatment or quarantine in the case of epidemics) will not compromise the privacy of the protected.

The key elements of our model include the following:

• i)Network data collected over a population of individuals and consisting of pairwise contacts (physical, social, electronic, financial, etc.). The contacts or links of each individual comprise the private data they desire to protect. We assume a third party (such as an intelligence agency or medical organization) has direct access to this network data, and would like to discover and act upon targeted individuals.
• ii)For each individual, an immutable “status bit” that determines their membership status in the targeted subpopulation (such as terrorism or infection). These status bits can be discovered by the third party, but only at some nontrivial cost (such as further surveillance or medical testing), and thus there is a budget limiting the number of status bits that an algorithm can reveal. One might assume or hope that in practice, this budget is sufficient to investigate a number of individuals that is of the order of the targeted subpopulation size (so they can all be discovered), but considerably less than that needed to investigate every member of the general population.
• iii)A mathematically rigorous notion of individual data privacy (based on the widely studied differential privacy; ref. 4) that provides guarantees of privacy for the network data of only the protected individuals, while allowing the discovery of targeted individuals. Informally, this notion guarantees that compared with a counterfactual world in which any protected individual arbitrarily changed any part of their data, or even removed themselves entirely from the computation, their risk (measured with respect to the probability of arbitrary events) has not substantially increased.

We emphasize two important points about our model. First, we assume that the process of investigating an individual to determine their status bit is unobservable, and leaks no information itself. This assumption is justified in some settings—for example, when the investigation involves secretly intercepting digital communications, like emails and phone calls, or when it involves performing tests on materials (like blood samples) or information already obtained. However, our model does not fit situations in which the investigations themselves are observable—for example, if the investigation requires interviewing an individual’s family, friends, and colleagues—because the very fact that an individual was chosen for an investigation (regardless of its outcome) might disclose their private data. The second point is that “privacy” is a word that has many meanings, and it is important to distinguish between the types of privacy that we aim to protect (see, for example, Solove’s taxonomy of privacy; ref. 5). Our goal is to quantify informational privacy—that is, how much information about a protected individual can be deduced from the output of an analysis. However, it is important to note that the status bit investigations our algorithms make, even if unobservable, are a privacy loss that Solove calls “intrusion.” Our results can be viewed as providing a quantitative trade-off between informational privacy and intrusion: using our algorithms, it is possible to guarantee more informational privacy at the cost of a higher degree of intrusion, and vice versa.

Our main results are:

• i)The introduction of a broad class of graph search algorithms designed to find and identify targeted individuals. This class of algorithms is based on a general notion of a statistic of proximity—a network-based measure of how “close” a given individual v is to a certain set of individuals S. For instance, one such closeness measure is the number of short paths in the network from v to members of S. Our (necessarily randomized) algorithms add noise to such statistics to prioritize which status bits to query (and thus how to spend the budget).
• ii)A theoretical result proving a quantitative privacy guarantee for this class of algorithms, where the level of privacy depends on a measure of the sensitivity of the statistic of proximity to small changes in the network.
• iii)Extensive computational experiments in which we demonstrate the effectiveness of our privacy-preserving algorithms on real social network data. These experiments demonstrate that in addition to the privacy guarantees, our algorithms are also useful, in the sense that they find almost as many members of the targeted subpopulation as their nonprivate counterparts. The experiments allow us to quantify the loss in effectiveness incurred by the gain in privacy.

Our formal framework is the first to our knowledge to introduce explicit protected and targeted subpopulations with qualitatively differing privacy rights. This is in contrast to the quantitative distinction proposed by Dwork and McSherry (6), which still does not allow for the explicit discovery of targeted individuals. We also note that our definition of privacy can be expressed in the Blowfish privacy framework (7) (although this had not previously been done). Our algorithms are the first to provide mathematically rigorous privacy guarantees for the protected while still allowing effective discovery of the targeted. More generally, we believe our work makes one of the first steps toward richer privacy models that acknowledge and manage the tensions between different levels of privacy guarantees to different subgroups.

Preliminaries

Consider a social network in which the individuals have an immutable status bit which specifies whether they are members of a targeted subpopulation or not (in which case we say they are part of the protected subpopulation). These status bits induce a partition on the population—we write $\mathcal{T}$ to denote the targeted subpopulation and $\mathcal{P}$ to denote protected subpopulation. Individuals correspond to the vertices V in the network, and the private data of each individual v is the set of edges incident to v. We assume that the value of an individual’s status bit is not easily observed, but can be discovered through (possibly costly) investigation. Our goal is to develop search algorithms to identify members of the targeted subpopulation, while preserving the privacy of the edge set of the protected population.

Any practical algorithm must operate under an investigation budget, which limits the number of status bits that are examined. Our goal is a total number of status bit examinations that is on the order of the size of the targeted subpopulation $\mathcal{T}$, which may be much smaller than the size of the protected population $\mathcal{P}$. This is the source of the tension we study—because the budget is limited, it is necessary to exploit the private edge set to guide our search (i.e., we cannot simply investigate the entire population), but we wish to do so in a way that does not reveal much about the edges incident to any specific protected individual.

The privacy guarantee we provide is a variant of differential privacy, an algorithmic definition of data privacy. It formalizes the requirement that arbitrary changes to a single individual’s private data should not significantly affect the output distribution of the data analysis procedure, and so guarantees that the analysis leaks little information about the private data of any single individual. We introduce the definition of differential privacy specialized for the network setting. We treat networks as a collection of vertices representing individuals, each represented as a list of its edges (which form the private data of each vertex). For a network G and a vertex v, let $D_v\left(G\right)$ be the set of edges incident to the vertex v in G. Let ${\mathcal{G}}_n$ be the family of all n vertex networks.

Definition 1. [Vertex differential privacy (4, 8–10)] The networks $G,G\prime$ in ${\mathcal{G}}_n$ are neighboring if one can be obtained from the other by an (arbitrary) rewiring of the edges incident to a single vertex v; i.e., if for some vertex v, $D_u\left(G\right)\mathrm{\setminus }\left\{\left(u,v\right)\right\}=D_u(G\prime )\mathrm{\setminus }\left\{\left(u,v\right)\right\}$ for all $u\ne v$. An algorithm ${A:\mathcal{G}}_n\to \mathcal{O}$ satisfies ε-differential privacy if for every event $S\subseteq \mathcal{O}$ and all neighboring networks ${G,G\prime \in \mathcal{G}}_n$,

$$\text{Pr}\left[\mathcal{A}\left(G\right)\in S\right]\le e^{\epsilon }\text{Pr}\left[\mathcal{A}(G\prime )\in S\right].$$

Differential privacy is an extremely strong guarantee—it has many interpretations (see discussion in ref. 11), but most straightforwardly, it promises the following: simultaneously for every individual v, and simultaneously for any event S that they might be concerned about, event S is almost no more likely to occur given that individual v’s data is used in the computation, compared with if it were replaced by an arbitrarily different entry. Here, “almost no more likely” means that the probability that the bad event S occurs has increased by a multiplicative factor of at most $e^{\epsilon }$, which we term the risk multiplier. As the privacy parameter ε approaches 0, the value of the risk multiplier approaches 1, meaning that individual v’s data has no effect at all on the probability of a bad outcome. The smaller the risk multiplier, the more meaningful the privacy guarantee. It will be easier for us to reason directly about the privacy parameter ε in our analyses, but semantically it is the risk multiplier $e^{\epsilon }$ that measures the quality of the privacy guarantee, and it is this quantity that we report in our experiments.

Differential privacy promises the same protections for every individual in a network, which is incompatible with our setting. We want to be able to identify members of the targeted population, and to do so, we want to be able to make arbitrary inferences from their network data. Nevertheless, we want to give strong privacy guarantees to members of the protected subpopulation. This motivates our variant of differential privacy, which redefines the neighboring relation between networks. In contrast to the definition of neighbors given above, we now say that two networks are neighbors if and only if one can be obtained from the other by arbitrarily rewiring the edges incident to a single member of the protected population only. Crucially, two networks are not considered to be neighbors if they differ in either:

• i)The way in which they partition vertices between the protected and targeted populations $\mathcal{P}$ and $\mathcal{T}$, or
• ii)any edges that connect pairs of vertices $u,v\in \mathcal{T}$ that are both members of the targeted population.

What this means is that we are offering no guarantees about what an observer can learn about either the status bit of an individual (protected vs. targeted), or the set of edges incident to targeted individuals. However, we are still promising that no observer can learn much about the set of edges incident to any member of the protected subpopulation. This naturally leads us to the following definition:

Definition 2. (Protected differential privacy) Two networks $G,G\prime$ in ${\mathcal{G}}_n$ are neighboring if they:

• i)Share the same partition into $\mathcal{P}$ and $\mathcal{T}$, and
• ii)G can be obtained from $G\prime$ by rewiring the set of edges incident to a single vertex $v\in \mathcal{P}$.

An algorithm $\mathcal{A}:{\mathcal{G}}_n\to \mathcal{O}$ satisfies ε-protected differential privacy if for any two neighboring networks $G,G\prime \in {\mathcal{G}}_n$, and for any event $S\subseteq \mathcal{O}$:

$$\text{Pr}\left[\mathcal{A}\left(G\right)\in S\right]\le e^{\epsilon }\text{Pr}\left[\mathcal{A}(G\prime )\in S\right].$$

Formally, our network analysis algorithms take as input a network and a method by which they may query whether vertices v are members of the protected population $\mathcal{P}$ or not. The class of algorithms we consider are network search algorithms—they aim to identify some subset of the targeted population. Our formal model is agnostic as to what action is ultimately taken on the identified members (for example, in a medical application they might be quarantined, in a security application they might be arrested, etc.). From the perspective of informational privacy, all that is relevant is that which members of the targeted population we ultimately identify is observable. Hence, without loss of generality we can abstract away the action taken and simply view the output of the mechanism to be an ordered list of individuals who are confirmed to be targeted.

Our privacy definition promises that what an observer learns about an individual “Alice” (e.g., that Alice is in contact with a particular individual Bob, or an entire class of individuals, such as members of a religious group) is almost independent of Alice’s connections, so long as Alice is not herself a member of the targeted population. On the other hand, it does not prevent an observer from learning that Alice exists at all. This models a setting in which (for example) a national government has access to an index of all of its citizens (through birth and immigration records), but nevertheless would like to protect information about their interactions with each other.

We note that the Blowfish privacy framework gives a general definition of privacy with different neighboring relations (7). Our definition can be seen as an instantiation of this general framework. This is in contrast to other kinds of relaxations of differential privacy, which relax the worst-case assumptions on the prior beliefs of an attacker as in Bassily et al. (12), or the worst-case collusion assumptions on collections of data analysts as in Kearns et al. (13). Several works have also proposed assigning different differential privacy parameters to different individuals (see, e.g., ref. 14). However, this is not compatible with identifying members of a targeted population.

Algorithmic Framework

The key element in our algorithmic framework is the notion of a statistic of proximity (SoP), a network-based measure of how close an individual is to another set of individuals in a network. Formally, an SoP is a function f that takes as input a graph G, a vertex v, and a set of targeted vertices $S\subseteq \mathcal{T}$, and outputs a numeric value $f\left(G,v,S\right)$. Examples of such functions include the number of common neighbors between v and the vertices in S, and the number of short paths from v to S. In our use, when we compute a statistic of proximity, the set S will always be the set of vertices confirmed through the status bit investigations so far to be members of the targeted population. Hence, the SoP should be viewed as a measure of closeness in the network to the known portion of the targeted subnetwork.

Algorithms in our framework rely on the SoP to prioritize which status bits to examine. Because the value of the SoP depends on the private data of a vertex, we perturb the values of the SoP by adding noise with scale proportional to its sensitivity, which captures the magnitude by which a single protected vertex can affect the SoP of some targeted vertex. The sensitivity of the SoP f, denoted $\mathrm{\Delta }\left(f\right)$, is defined to be the maximum of $\left|f\left(G,t,S\right)-f\left(G\prime ,t,S\right)\right|$ over all choices for the subset $\mathcal{T}$ of targeted vertices, all neighboring pairs of graphs G and $G\prime$, all $t\in \mathcal{T}$, and all $S\subseteq \mathcal{T}$. Crucially, note that in this definition—in contrast to what is typically required in standard differential privacy—we are only concerned with the degree to which a protected individual can affect the SoP of a targeted individual.

We next describe the nonprivate version of our search algorithm $\mathrm{Target}\left(k,f\right)$. Our motivation in choosing this particular algorithm is simplicity: it is the most straightforward type of contact chaining algorithm that ignores privacy entirely, and simply uses the given SoP to prioritize investigations.

For any fixed SoP f, $\mathrm{Target}$ proceeds in k rounds, each corresponding to the identification of a new connected component in the subgraph induced by $\mathcal{T}$. The algorithm must be started with a seed vertex—a preidentified member of the targeted population. Each round of the algorithm consists of two steps:

• i)Statistic-first search: Given a seed targeted vertex, the algorithm iteratively grows a discovered component of targeted vertices, by examining, in order of their SoP values (computed with respect to the set S of individuals already identified as being members of the targeted population), the vertices that neighbor the previously discovered targeted vertices. This continues until every neighbor of the discovered members of the targeted population has been examined, and all of them have been found to be members of the protected population. We note that this procedure discovers every member of the targeted population that is part of the same connected component as the seed vertex, in the subgraph induced by only the members of the targeted population.
• ii)Search for a new component: Following the completion of statistic-first search, the algorithm must find a new vertex in the targeted population to serve as an initial vertex to begin a new round of statistic-first search. To do this, the algorithm computes the value of the SoP for all vertices whose status bit has not already been examined, using as the input set S the set of already discovered members of the targeted population. It then sorts all of the vertices in decreasing order of their SoP value, and begins examining their status bits in this order. The first vertex that is found to be a member of the targeted population is then used as the seed vertex in the next round. In the SI Appendix, we present a slight variant of this procedure that instead of running for a fixed number of rounds, allows the search algorithm to halt if it is unable to find any new targeted vertices after some number of examinations.

The algorithm outputs discovered targeted individuals as they are found, and so its output can be viewed as being an ordered list of individuals who are confirmed to be from the targeted population.

The private version of the targeting algorithm $\mathrm{PTarget}\left(k,f,\epsilon \right)$, is a simple variant of the nonprivate version. The statistic-first search stage remains unchanged, and only the search for a new component is modified via randomization. In the private variant, when the algorithm computes the value of the SoP f on each unexamined vertex, it then perturbs each of these values independently with noise sampled from the Laplace distribution $\text{Lap}\left(△\left(f\right)/\epsilon \right)$, where ε is a parameter. [We use $\text{Lap}\left(b\right)$ to denote the Laplace distribution centered at 0 with probability density function: $\text{Pr}\left(x\right)=(1/2b)\text{exp}\left(-\left|x\right|/b\right)$]. Finally, it examines the vertices in sorted order of their perturbed SoP values.

We prove the following theorem, deferring details of the proof and the algorithm to the SI Appendix:

Theorem 1. Given any $k\ge 1$ and $\epsilon >0$ and a fixed SoP f, the algorithm $\mathit{PTarget}\left(k,\hspace{0.17em}f,\epsilon \right)$ recovers k connected components of the subgraph induced by the targeted vertices and satisfies $\left(\left(k-1\right)\cdot \epsilon \right)$-protected differential privacy.

There are two important things to note about this theorem. First, we obtain a privacy guarantee despite the fact that the statistic-first search portion of our algorithm is not randomized—only the search for new components employs randomness. Intuitively, the reason that statistic-first search can remain unmodified and deterministic is that as long as we remain with a connected component of targeted vertices, we will eventually output only those vertices, and thus we are not compromising the privacy of protected vertices. It is only when we search for a new targeted component via protected vertices and the SoP that we must randomize—for instance to provide privacy to protected “bridge” vertices between targeted components. See the SI Appendix for the detailed technical argument.

Second, the privacy cost of the algorithm grows only with k, the number of disjoint connected components of targeted individuals (disjoint in the subgraph defined on targeted individuals), and not with the total number of individuals examined, or even the total number of targeted individuals identified. Hence, the privacy cost can be very small on graphs in which the targeted individuals lie only in a small number of connected components or “cells.” Both of these features are unusual compared with typical guarantees that one can obtain under the standard notion of differential privacy.

Because $\mathrm{PTarget}$ adds randomness for privacy, it results in examining a different set of vertices compared with $\mathrm{Target}$. Fig. 1 provides a sample visualization of the contrasting behavior of the two algorithms. Although theorems comparing the utility of $\mathrm{Target}$ and $\mathrm{PTarget}$ are possible, they require assumptions ensuring that the chosen SoP is sufficiently informative, in the sense of separating the targeted from the protected by a wide enough margin. In particular, one needs to rule out cases in which all unexplored targeted vertices are deemed closer to the current set than all protected vertices, but only by an infinitesimal amount, in which case the noise added by $\mathrm{PTarget}$ eradicates all signal. In general such scenarios are unrealistic, so instead of comparing utility theoretically, we now provide an extensive empirical comparison.

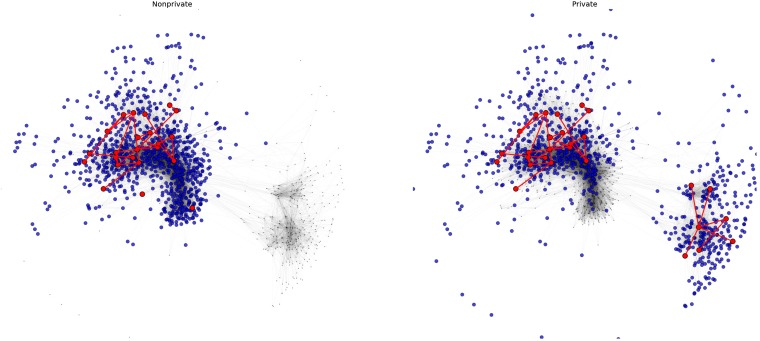
Fig. 1.

Visual comparison of the nonprivate algorithm $\mathrm{Target}$ (Left) and the private algorithm $\mathrm{PTarget}$ (Right) on a small portion of the IMDB network (see Experimental Evaluation for more details). For each algorithm, blue indicates protected vertices that have been examined, red indicates targets that have been examined, and gray vertices have not been examined yet. Both algorithms begin with the same seed target vertex, and by directed statistic-first search discover a subnetwork of targeted individuals (central red edges). As a consequence, many protected vertices are discovered and examined as well. Due to the added noise, $\mathrm{PTarget}$ explores the network in a more diffuse fashion, which in this case permits it to find an additional subnetwork of targets toward the right side of the network. The primary purpose of the noise, however, is for the privacy of protected vertices.

Experimental Evaluation

In this section we empirically demonstrate the utility of our private algorithm $\mathrm{PTarget}$ by comparing its performance to its nonprivate counterpart $\mathrm{Target}$. (No institutional approval was required for the experiments described.) We report on computational experiments performed on real social network data drawn from two sources—the paper coauthorship network of the Digital Bibliography and Library Project (DBLP) (dblp.uni-trier.de/xml/), and the coappearance network of film actors of the Internet Movie Database (IMDB) (www3.ul.ie/gd2005/dataset.html), whose macroscopic properties are described in Table 1.

Table 1.

Social network datasets used in the experiments

Network	No. vertices	No. edges	Edge relation
DBLP	956,043	3,738,044	Scientific paper coauthorship
IMDB	235,710	4,587,715	Movie coappearance

These data sources provide us with naturally occurring networks, but not a targeted subpopulation. Although one could attempt to use communities within each network (e.g., all coauthors within a particular scientific subtopic), our goal was to perform large-scale experiments in which the component structure of targeted vertices (which we shall see is the primary determinant of performance) could be more precisely controlled. We thus used a simple parametric stochastic diffusion process (described in the SI Appendix) to generate the targeted subpopulation in each network. We then evaluate our private search algorithm $\mathrm{PTarget}$ on these networks, and compare its performance to the nonprivate variant $\mathrm{Target}$. For brevity we shall describe our results only for the IMDB network; results for the DBLP network are quite similar.

In our experiments, we fix a particular SoP between v and S: the size of the union, across all w in S, of the common neighbors of v and w. Here S is the subset of vertices representing the already discovered members of the targeted population. This SoP has sensitivity 1, and so can be used in our algorithm while adding only a small amount of noise. In particular, the private algorithm $\mathrm{PTarget}$ adds noise sampled from the Laplace distribution $\text{Lap}\left(20\right)$ to the SoP when performing new component search. By Theorem 1, such an instantiation of $\mathrm{PTarget}$ guarantees $\left(\left(k-1\right)/20\right)$-protected differential privacy if it finds k targeted components.

The main trade-off we explore is the number of members of the targeted population that are discovered by the algorithms (the y axis in the ensuing plots), as a function of the budget, or number of status bits that have been investigated so far (the x axis in the ensuing plots). In each plot, the parameters of the diffusion model described above were fixed and used to stochastically generate targeted subpopulations of the fixed networks given by our social network data. By varying these parameters, we can investigate performance as a function of the underlying component structure of the targeted subnetwork. As we shall see, in terms of relative performance, there are effectively three different regimes of the diffusion model (i.e., targeted subpopulation) parameter space. In all of them $\mathrm{PTarget}$ compares favorably with $\mathrm{Target}$, but to different extents and for different reasons that we now discuss. We also plot the growth of the risk multiplier for $\mathrm{PTarget}$, which remains less than 2 in all three regimes.

On each plot, there is a single blue curve showing the performance of the (deterministic) algorithm $\mathrm{Target}$, and multiple red curves showing the performance across 200 runs of our (randomized) algorithm $\mathrm{PTarget}$.

The first regime (Fig. 2) occurs when the largest connected component of the targeted subnetwork is much larger than all of the other components. In this regime, if both algorithms begin at a seed vertex inside the largest component, there is effectively no difference in performance, as both algorithms remain inside this component for the duration of their budget and find identical sets of targeted individuals. More generally, if the algorithms begin at a seed outside the largest component, relative performance is a race to find this component; the private algorithm lags slightly due to the added noise, but is generally quite competitive; see Fig. 2 for details.

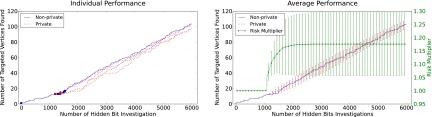
Fig. 2.

Performance for the case in which there is a dominant component in the targeted subpopulation. In Left, we show the number of targeted vertices found as a function of the budget used for both the (deterministic) nonprivate algorithm $\mathrm{Target}$ (blue), and for several representative runs of the randomized private algorithm $\mathrm{PTarget}$ (red). Colored circles indicate points at which the corresponding algorithm has first discovered a new targeted component. In Right, we show average performance over 200 trials for the private algorithm with 1-SD error bars. We also show the private algorithm risk multiplier with error bars. In this regime, after a brief initial flurry of small component discovery, both algorithms find the dominant component, so the private performance closely tracks nonprivate, and the private algorithm’s risk multiplier quickly levels off at around only 1.17.

The second regime (Fig. 3) occurs when the component sizes are more evenly distributed, but there remain a few significantly larger components. In this setting both algorithms spend more of their budget outside the targeted subpopulation “searching” for these components. Here the performance of the private algorithm lags more significantly—because both algorithms behave the same when inside of a component, the smaller the components are, the more detrimental the noise is to the private algorithm (though again we see particular runs in which the randomness of the private algorithm permits it to actually outperform the nonprivate).

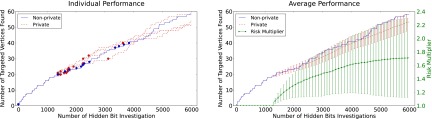
Fig. 3.

Same format as in Fig. 2, but now in a case where the component sizes are more evenly distributed, but still relatively large. The performance of both algorithms is hampered by longer time spent investigating nontargeted vertices (note the smaller scale of the y axis compared with Fig. 2). Targeted component discovery is now more diffuse. The private algorithm remains competitive but lags slightly, and as per Theorem 1 the risk multiplier grows (but remains modest) as more targeted components are discovered.

The third regime (Fig. 4) occurs when all of the targeted components are small, and thus both algorithms suffer accordingly, discovering only a few targeted individuals; but again the private algorithm compares favorably with the nonprivate, finding only a few less targeted vertices.

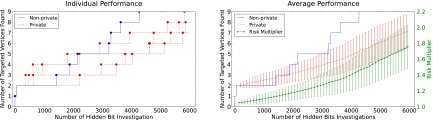
Fig. 4.

A case with a highly fragmented targeted subpopulation. Both algorithms now spend most of their budget investigating nontargeted vertices and suffer accordingly.

Conclusion

We view the work presented here as a proof of concept: despite the fact that using network analysis to identify members of a targeted population is intrinsically contrary to the privacy of the targeted individuals, we have shown that there is no inherent reason why informational privacy guarantees cannot be given to individuals who are not members of the targeted population, and that these privacy guarantees need not severely harm our ability to find targeted individuals. Our work is of course not a complete solution to the practical problem, which can differ from our simple model in many ways. Here we highlight just one interesting modeling question for future work: Is it possible to give rigorous privacy guarantees to members of the protected population when membership in the targeted population is defined as a function of the individuals’ private data? In our model, we avoid this question by endowing the algorithm with a costly “investigation” operation, which we assume can infallibly determine an individual’s targeted status—but it would be interesting to extend our style of analysis to situations in which this kind of investigation is not available.