Figure 5.

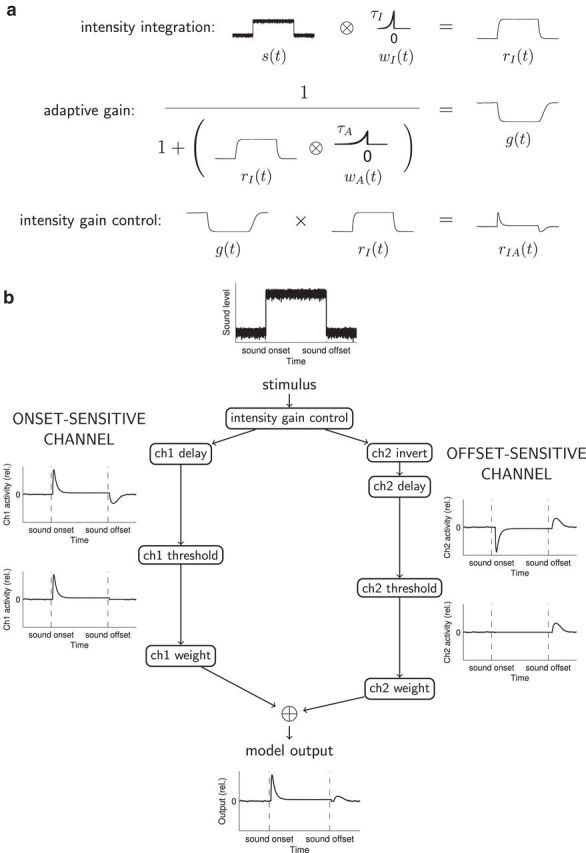
Conceptual explanation of the model. a, Graphical description of integration and adaptation computations producing intensity gain control. Time-varying sound level s(t) is convolved with the causal integration window w_I(t) to obtain r_I(t), the integrated stimulus input. Then, a time-varying gain function g(t) is computed using a simple version of the standard normalization equation (Carandini and Heeger, 2012), with convolution of r_I(t) and the causal adaptation window w_A(t) in the denominator. This adaptive gain g(t) is multiplied time point by time point with the integrated stimulus input r_I(t) to obtain the integrated and adapted function r_IA(t), incorporating intensity gain control. b, Diagram of the full two-channel model. The time-varying sound level forms the input to an intensity gain control process as outlined in a. In the onset-sensitive channel (ch1), intensity gain control computations are followed by a delay, then thresholding, then weighting before summation with channel 2 output. In the offset-sensitive channel (ch2), intensity gain-control computations are followed by inversion and a longer delay than in ch1; the weighting of ch2 after thresholding is also reduced relative to that of ch1. Model output is the sum of the weighted activity in the two channels. All plots of channel activity and model output show activity relative to that produced by extended “silence” (simulated as very low-level noise). For simulations shown in Figures 6 and 7, “nonectopic” model parameters were as follows: integration τ_I = 6 ms, adaptation τ_A = 10 ms; onset-sensitive channel delay = 5 ms, weight = 1.0; offset-sensitive channel delay = 13 ms, weight = 0.5. “Ectopic” model parameters were identical, except that the weighting of the offset-sensitive channel was reduced to 0.25.