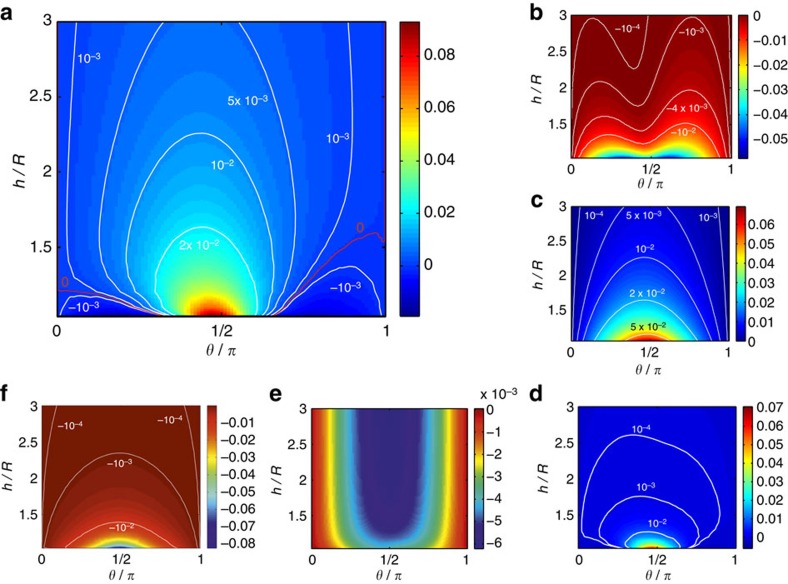
Figure 3. Various contributions to particle angular velocity Ωx.
(a) Contribution from self diffusiophoresis 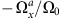 (see Supplementary Note 2 and equation (2) as a function of height h/R and orientation θ for half-covered Janus microswimmer and unequal surface mobilities binert/bcap=0.3. Throughout, white curves correspond to constant values of
(see Supplementary Note 2 and equation (2) as a function of height h/R and orientation θ for half-covered Janus microswimmer and unequal surface mobilities binert/bcap=0.3. Throughout, white curves correspond to constant values of 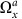 . Note that, by definition, panel a is the sum of panels b,c, and d. (b), Contribution
. Note that, by definition, panel a is the sum of panels b,c, and d. (b), Contribution 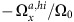 obtained by using the free space number density of solute distribution cfs(r) around the particle, i.e., neglecting the influence of the wall on the number density of solute, but including the influence of the wall on the hydrodynamic flow. (c) Contribution
obtained by using the free space number density of solute distribution cfs(r) around the particle, i.e., neglecting the influence of the wall on the number density of solute, but including the influence of the wall on the hydrodynamic flow. (c) Contribution 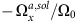 obtained by using the free space hydrodynamics stress tensor
obtained by using the free space hydrodynamics stress tensor 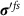 in the dual Stokes problems employed in the reciprocal theorem, i.e., neglecting the effect of the wall on the hydrodynamics, but including the chemical effect. (d) Contribution
in the dual Stokes problems employed in the reciprocal theorem, i.e., neglecting the effect of the wall on the hydrodynamics, but including the chemical effect. (d) Contribution 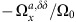 due to higher order coupling between the two effects. (e) Contribution to rate of rotation from the bottom-heaviness of the particle. (f) Chemio-osmotic contribution
due to higher order coupling between the two effects. (e) Contribution to rate of rotation from the bottom-heaviness of the particle. (f) Chemio-osmotic contribution 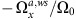 due to the activity-induced phoretic slip at the wall calculated at bw/bcap=−0.2.
due to the activity-induced phoretic slip at the wall calculated at bw/bcap=−0.2.