Advances in the Determination of Nucleic Acid Conformational Ensembles

Abstract

Conformational changes in nucleic acids play a key role in the way genetic information is stored, transferred, and processed in living cells. Here, we describe new approaches that employ a broad range of experimental data, including NMR derived chemical shifts and residual dipolar couplings, small angle X-ray scattering, and computational approaches such as molecular dynamics simulations, to determine ensembles of DNA and RNA at atomic resolution. We review the complimentary information that can be obtained from diverse sets of data and the various methods that have been developed to combine these data with computational methods to construct ensembles and assess their uncertainty. We conclude by surveying RNA and DNA ensembles determined using these methods, highlighting the unique physical and functional insights that have been obtained so far.

1. Introduction

There is growing interest in the dynamic properties of nucleic acids because changes in the structure and dynamics of RNA(1; 2) and DNA(3; 4) play essential roles in how genetic information is stored, accessed, transferred, and processed in living cells. Insights into the dynamic properties of nucleic acids is also important for achieving a predictive understanding of how a polynucleotide chain folds into a 3D structure(5), and also for realizing a number of important biotechnological applications, including the design of nucleic acid-targeting therapeutics and nucleic-acid based devices(6–8).

Much of the dynamic properties that are of interest are encoded in the free energy landscape, which provides a thermodynamic and kinetic description of the ensemble of conformations that are sampled by a nascent nucleic acid in solution(2; 9). The population of a given conformation is dependent on its relative free energy, while the rates at which two conformations inter-convert is dictated by their free energy barrier of separation. Cellular cues perturb the free energy landscape, and thereby effect changes in nucleic acid structure and dynamics that lead to desired biological outcomes.

Important insight into the free energy landscape can be obtained by measuring internal motions in the nucleic acid over a broad range of timescales. This can provide direct information regarding the populations of different conformations and their rates of inter-conversion. Determining the entire free energy landscape and every aspect of the conformational ensemble through such dynamics measurements is generally not feasible, because it is hard to measure the rates of transitions between each and every conformations and also due to the fact that many conformations exist in low abundance and/or for short periods of time, thus evading experimental detection. Instead, studies have attempted to describe the distribution of the most populated conformations (typically >1%) representing the lowest energetic minima along the free energy landscape. The focus has been on the structure and populations of these states, and less so the rates at which they interconvert, which proves difficult to measure experimentally. Throughout this review, we will refer to this reduced thermodynamic description as a ‘conformational ensemble’.

Determining conformational ensembles for complex biomolecules at atomic resolution presents a significant challenge compared to other high-resolution structure characterization techniques such as X-ray diffraction. First, a much larger number of parameters need to be defined as compared to a static structure, and measuring these parameters can prove arduous, particularly for highly disordered systems. Second, as mentioned above, many conformers in a dynamic ensemble exist in low abundance or for very short periods of time, and therefore, are hard to detect experimentally. Finally, it can be difficult to assess the accuracy and precision of a determined ensemble. Here, we review recent advances that start to address these challenges culminating in the determination of DNA and RNA ensembles at near atomic resolution.

2. Experimental data

There are three important considerations in selecting experimental data to determine conformational ensembles. First, the data has to be sensitive to the structural degrees of freedom that are of interest. In general, the experimental parameters measured may be sensitive to different aspects of structure, e.g. global versus local structure, or rotational versus translation degrees of freedom. Obtaining an accurate all-atom ensemble will often require the combination of different types of data, and this in it of itself, can be a challenge (vide infra). Second, it must be possible to compute the experimental data for a given conformational ensemble. Depending on the type of data, it may be necessary to have additional information regarding constants that factor into the measurements, or the rates at which the conformers interconvert. The inverse problem, solving the “real ensemble” from a set of experimental data, or the range of ensembles that satisfy a given set of experimental observables, is generally difficult to address. Finally, different types of data may experience averaging at different timescales, complicating their combination in the ensemble determination. Other factors that can complicate combination of different data include use of different sample concentrations and attachment of different chemical probes that may differentially interfere with the nucleic acid conformational ensemble.

In what follows, we review the different types of experimental data that have been used in determining ensembles of nucleic acids, and also provide a brief overview of other types of data that may potentially be used in the ensemble determination in the future.

2.1 Small Angle X-ray Scattering

Small-Angle X-ray Scattering (SAXS) is an ideal tool to characterize global aspects of nucleic acid conformational ensembles. SAXS is a technique in which the elastic scattering of X-rays is measured at very low angles (typically 0.1º-10º), thus providing information about the overall shape and size of biomolecules that are 5 nm to 25 nm in size, with lower scattering angles allowing even larger dimensions to be resolved. Unlike X-ray crystallography, SAXS does not require a crystalline sample and can be performed under a variety of solution conditions(10). However, owing to the random reorientation of molecules, ensemble averaging leads to lower resolution structural information as compared to X-ray crystallography.

The SAXS scattering profile Δρ(r) is derived from the difference in scattering between the averaged electron density of the biomolecule ρ(r) and the bulk solvent ρ_S(r) and reflects the sum of scattering profiles for each atom-pair (Figure 1A). In principle, higher sample concentrations would give rise to more intense scattering profiles, however, in practice, experiments are performed under sufficiently dilute solutions to avoid non-specific aggregation. Fortunately, nucleic acids are ideal molecules for SAXS measurements because electron rich phosphate groups provide favorable contrast allowing use of much lower sample concentrations as compared to proteins(11–13).

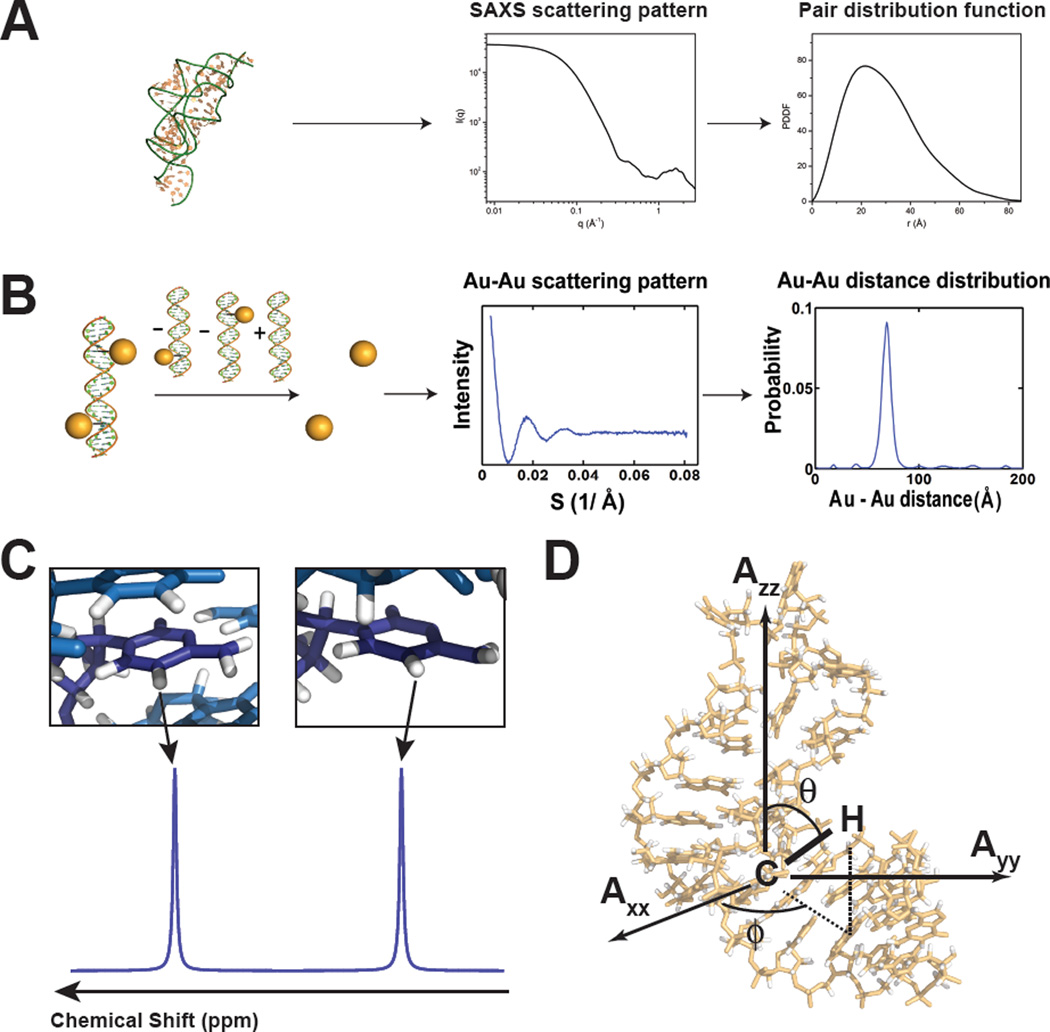
Figure 1.

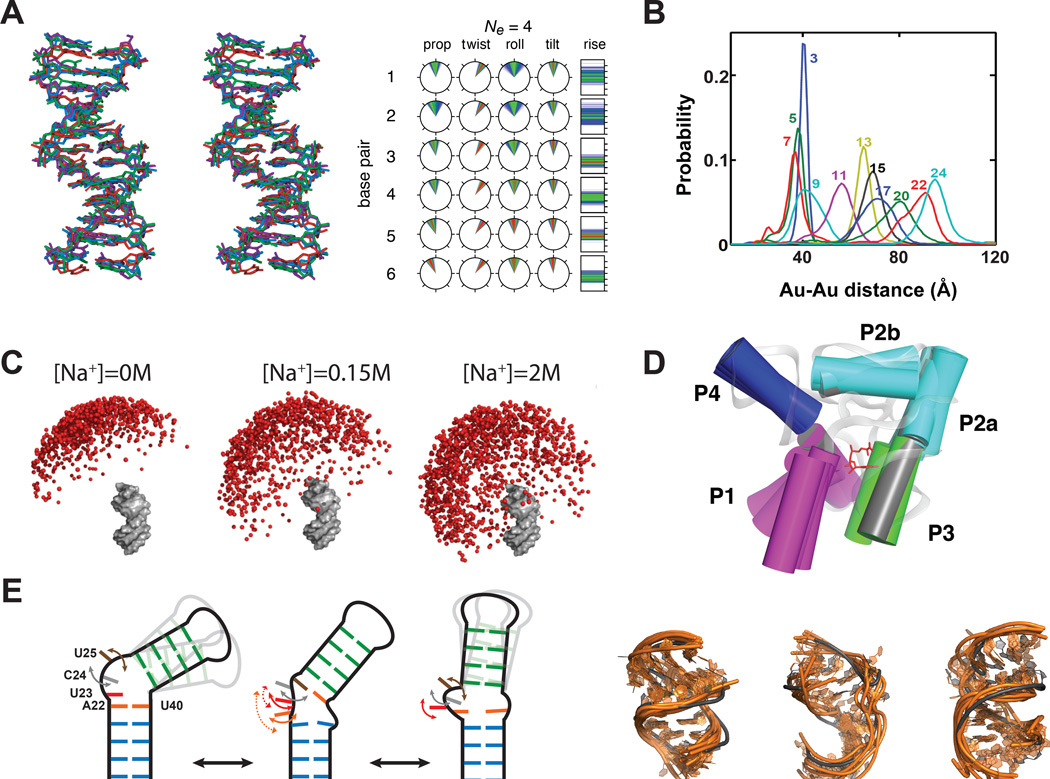
Experimental data used in ensemble determination of nucleic acids. (A) SAXS profile for an RNA and the corresponding pair distribution function. Adapted from Wang et al.(18) (B) Au-SAXS measurement of probability distance distributions for two attached gold nanocrystal probes. Adapted from Shi et al.(23) (C) NMR chemical shifts are sensitive to electronic environment and local structure. (D) NMR residual dipolar couplings provide angular information on the orientation of bond relative to the overall molecular alignment frame (A_xx, A_yy, A_zz).

Indirect Fourier transformation of the scattering profile I(q) maps it from reciprocal space (r⁻¹) to a pair distribution function P(r) in real space (r)(12) (Figure 1A), which is a population-weighted distribution of distances for all atom-pairs within the biomolecule. Although it is difficult to uniquely determine P(r) from I(q), the latter can be calculated from a given biomolecule structure with defined P(r) using the Debye equation under the assumption that the solution is an isolated scattering system and each atom in the solution is a spherical scatterer(14). Direct use of the Debye equation can be computationally expensive, and approximations are often introduced in order to accelerate the calculations(11; 12; 14–17). A growing number of studies have demonstrated the power of integrating SAXS data with NMR restraints in the structure determination of large complex RNAs(18–20).

Instead of constructing pair distance distribution functions P(r) for all atom-pair within the biomolecule, recently developed gold SAXS (Au-SAXS) methods allow the determination of precise distance distributions from two externally anchored scatterer, namely gold nanocrystals that are attached at specific positions on the nucleic acid (Figure 1B)(21–23). The scattering profile between two attached gold nanocrystals is isolated from the intra-nanocrystal, intra-nucleic acid, and nucleic acid-nanocrystal interference pattern by subtracting the scattering profile measured for isolated gold nanocrystals, isolated nucleic acid, and singly-labeled nucleic acid from the scattering profile measured for the double-labeled nucleic acid (Figure 1B)(21–23). Motions of the gold nanocrystal relative to the nucleic acid can influence the scattering profile and these contributions can be minimized by using less flexible linkers to anchor the gold nanocrystal onto the nucleic acid(21; 22; 24). Control experiments are preformed to ensure that the relatively large gold nanocrystals do not interfere with the structure and dynamic properties of the nucleic acid(21; 22).

For a biomolecule in exchange between several conformations, the SAXS profiles will in principle represent the sum of contributions from each conformation in the sample, because the light matter interaction occurs at timescales much faster than the conformational change. This renders SAXS insensitive to the precise timescales of the motion, allowing for easier interpretation in constructing ensembles(25). However, due to its low resolution, for system that do not exhibit large conformational changes, the observed scattering profile can often be interpreted in terms of a single conformation(10).

It should be noted that small angle neutron scattering (SANS) can also be used to obtain dynamics information and in combination with appropriate isotopic labeling schemes can provide structural information on specific sub-domains in a complex system(26–29).

2.2 Chemical Shifts

The Nuclear Magnetic Spectroscopy (NMR) chemical shift (CS) is one of the simplest parameters to measure using solution state NMR. The chemical shift is the resonant frequency of a nucleus relative to a reference frequency. It is determined by the effective magnetic field experienced by a given nucleus: in addition to the applied NMR magnetic field, a given nucleus experiences local magnetic fields induced by currents due to electrons in molecular orbitals. For a given nucleus type (¹H, ¹³C, ¹⁵N, and ³¹P), this electronic distribution will depend on local aspects of the structure, including bond lengths, dihedral angles, hydrogen bonding, protonation state as well as ring current effects arising due to circulation of π-electrons in the aromatic nucleobases, magnetic anisotropy, and other electrostatic effects(30) (Figure 1C). For a dynamic ensemble, the observed CS at a given nucleus will correspond to a population weighted average over all conformations provided that the rates of inter-conversion between conformers is larger than the corresponding difference between their chemical shifts (commonly referred to as the fast “exchange limit”). CSs are exquisite probes of local structure, but generally provide limited information about long-range aspects of structure.

The growth in the database of protein structures with corresponding NMR ¹H, ¹³C, and ¹⁵N resonance assignments has allowed the development of powerful methods for computing chemical shifts based on 3D structure, and these approaches are increasingly being used in the determination of protein conformational ensembles(31; 32). By comparison, the database of nucleic acid structures with corresponding NMR resonance assignments is much smaller. Because of this, methods to compute CSs from a given nucleic acid structure remain underdeveloped and difficult to test rigorously. Several approaches have been developed to compute ¹H(33–35) based in nucleic acid structure. The accuracy with which chemical shifts can be computed from structure based on these approaches is sufficiently good to allow their utility in 3D structure determination and in characterizing motions in highly locally mobile regions in a structure(36). The accuracy with which CS data can be computed based on 3D structure remains, however, sub-optimal for determining ensembles, though the CS data can be used to test ensembles determined using other methods(36). One drawback in some of these approaches is that the motionally averaged experimental CS database is parameterized assuming single static structures, making it more difficult to identify cases in which motional averaging has taken place. Quantum mechanical approaches, such as density functional theory (DFT) calculations, can be used to compute the corresponding chemical shifts for static structure(37). While these calculations are generally very time-consuming, and therefore difficult to implement in an ensemble determination, the DFT computed chemical shifts can be empirically parameterized to develop simpler structure-CS relationships, as demonstrated recently by Vendruscolo and co-workers in the interpretation of ribose ¹³C chemical shifts(38). Considering the growing database of nucleic structures determined by NMR, methods to compute ¹H, ¹³C, ¹⁵N and ³¹P CSs will likely improve at a rapid pace allowing their integration in ensemble determination.

2.3 Anisotropic NMR interactions: RDCs and RCSAs

Many NMR interactions such as dipolar couplings and chemical shift anisotropy (CSA) are second rank interactions that depend on the orientation of dipolar and CSA tensors centered on nuclei of interest relative to the applied magnetic field. To understand these anisotropic interactions, consider the dipolar coupling between two spin i and j. In solution NMR, a given nucleus i experiences the sum of the external magnetic field as well as the magnetic field generated by a directly bonded nucleus j and other nuclei in its vicinity. The latter contribution depends on the cube of the distance separating the two nuclei, which is the bond length for directly bonded spins, as well as on the angle, ϑ, between the inter-nuclear bond vector and the applied magnetic field, as described by the angular term $\frac{3{\text{cos}}^2\vartheta -1}{2}$. In solution NMR, this magnetic dipole-dipole interaction, and in particular the angular term, time-averages to zero due to random Brownian rotational diffusion, and indeed, the loss of these otherwise very large interactions is one of the main reasons solution NMR exhibits high-resolution and sharp lines. However, by imparting a small degree of order on a biomolecule, corresponding to ordering on the order of 10⁻³ −10⁻⁵ , one can break the isotropic averaging and re-introduce a fraction of the dipolar interaction while preserving the high quality of solution state NMR spectra. This dipolar interaction manifests as an additional contribution to one bond ¹J-couplings for two directly bonded nuclei and is referred to as a ‘residual dipolar coupling’ (RDC). Nucleic acids samples can be aligned spontaneously due to interactions with the magnetic field itself(39; 40), or by dissolution in an ordering medium such as filamentous bacteriophage(41; 42).

An expression for the RDC measured for two nuclei i and j in an N^th conformer is given by(43–45):

$$D_{\mathit{\text{ij}}}^N=-\frac{{\mu }_0{\gamma }_i{\gamma }_{j}h}{16{\pi }^3{r}_{\mathit{\text{ij}}}^3}\left[A_a^N\right(3{\text{cos}}^2{\theta }_{\mathit{\text{ij}}}^N-1)+\frac{3}{2}{A}_r^N({\text{sin}}^2{\theta }_{\mathit{\text{ij}}}^N\text{cos}2{\phi }_{\mathit{\text{ij}}}^N\left)\right]$$ (1)

where µ₀ is the magnetic permittivity of vacuum, h is Planck’s constant, γ_i and γ_j the gyromagnetic ratio of spins i and j, respectively, A_a and A_r are the axial and rhombic components of the overall alignment tensor describing overall alignment, r_ij is an effective averaged value of the inter-nuclear distance, θ and ϕ are the polar angles that carry the desired structural information describing the orientation of the inter-nuclear vector relative to the alignment tensor frame (Figure 1D). The RDCs are time-averaged over all conformations that are sampled at rates faster than the inverse of the dipolar interactions (typically < millisecond timescales)(43; 46). Commonly targeted RDCs in nucleic acids include the large one-bond C-H and N-H RDCs in the nucleobase and sugar moieties although experiments have also been developed to measure many other C-C, C-H, H-H and longer range interactions (reviewed in(47)). In the former cases, the distance between nuclei is assumed to be known based on knowledge of local geometry.

Computing RDCs for a given bond vector in a given conformation using Equation 1 requires the knowledge of the five alignment tensor parameters; A_a and A_r and three Euler angles describing the orientation of the alignment frame relative to the molecule(43–45). In general, the overall alignment tensor depends on the overall structure of the nucleic acid, and as a result, can vary between different conformers in an ensemble(48). Computing RDCs for a given conformation therefore requires the ability to independently determine the overall alignment tensor associated with that conformation. Two approaches can be used to address this problem. A target helix in the nuclei acid can be elongated such that the overall shape does not vary with internal motions in other parts of the molecule(49; 50). This fixed alignment tensor can be determined by subjecting RDCs measured in the elongated helix to a standard order tensor determination(51). Alternatively, methods such as PALES(48) can be used to compute four of the five alignment tensor parameters based on the nucleic acid structure, and the remaining fifth parameter describing the degree of order is treated as a variable that is optimized during the ensemble determination. Because the overall alignment tensor depends on the global molecular shape, RDCs are sensitive to both local and global aspect of structure and in particular the relative orientation of bond vectors and helices. It should be noted that in theory as many as five independent sets of RDCs can be measured in a given nucleic acid by changing how the sample is aligned relative to the magnetic field, thus providing additional data sets for construction ensembles with higher resolution(52; 53). This could be achieved by combining ordering media based alignment with magnetic field alignment(54; 55), vriable domain-elongation(56), and protein-binding modulated alignment(57).

Partial alignment also leads to incomplete averaging of the anisotropic component of the chemical shift, allowing measurements of so-called residual chemical shift anisotropies (RCSAs) as changes in chemical shift relative to the isotropic case(58; 59). These data report on the orientation of the CSA tensor, centered on the nucleus of interest, relative to the alignment tensor frame. In nucleic acids, ³¹P(60) and nucleobase ¹³C carbon(61; 62) RCSAs provide complimentary information to RDCs but their interpretation generally requires knowledge of the chemical shift anisotropy (CSA) tensor, which vary from site to site, and which can be difficult to determine a priori.

2.4 Scalar Couplings

NMR scalar couplings arise from coupled interactions between the electron and nuclear spins of two bonded nuclei that result in the splitting of NMR resonances. The magnitude of scalar couplings depends on the type of nuclei involved, the number of bonds separating them and the intervening dihedral angle in the case of three bond scalar couplings (³J). A large number of ³J_HH, ³J_HC, ³J_HP, and ³J_CP scalar couplings have been used to probe dihedral angles involving the sugar, base, and phosphodiester backbone and are often used in NMR structure determination of nucleic acids(63; 64) of nucleic acids using appropriate Karplus equations. Difficulties in parameterizing Karplus relations using databases containing motionally averaged scalar couplings, together with their limited structural resolution and inherent degeneracies have somewhat limited their widespread application. Nevertheless, scalar couplings have been used in nucleic acid ensemble determination in combination with other experimental data(15). Scalar couplings exhibit similar sensitivities to the timescales of motional averaging (up to the millisecond) as RDCs and CSs. Improvements in parameterization may increase the utility of scalar couplings in ensemble determination of nucleic acids in the future.

2.5 Other types of data

There are other types of data that have been used in structure but not in ensemble determination or in proteins but not in nucleic acids that we can expect will play important roles in the determination of nucleic acid ensembles in the future. NMR data include measurements of spin relaxation, such as ¹⁵N and ¹³C spin relaxation data which report primarily on the dynamics of bond vectors in biomolecules occurring at picosecond to nanosecond timescales(65); Paramagnetic Relaxation Enhancements (PREs) which depend on the distance between a given nucleus and an attached paramagnetic species, and which can report on low populated short-lived conformers in an ensemble (66; 67), and cross-relaxation (NOEs) which reports on the network of proton-proton distances (and orientations for anisotropic overall diffusion)(68; 69). Such relaxation data not only depend on the distribution of conformations in the ensemble, but also have a complex dependence on the rates with which various conformers interconvert and the timescales for overall rotational diffusion. While this added information can be tapped in the future to extract timescale information, it currently complicates using of these data in the ensemble determination. In addition, NMR relaxation dispersion techniques(70; 71) are making it possible to visualize low-populated (<10%) short-lived (lifetimes in the range of millisecond to microseconds) conformers in both DNA (72) and RNA (73).

Förster Resonance Energy Transfer (FRET)(74; 75) and Electron paramagnetic resonance (EPR)(76; 77) can be used to obtain distance information between fluorophores or spin labels, respectively that are specifically attached to the nucleic acid. These data also depend on the orientation and dynamics of the fluorophores or spin labels, and approximations often have to be made to extract distance information(76; 78–82). Powerful single molecule approaches, such as single molecule FRET (smFRET) can be used to directly measure transitions within a single molecule and obtain information about the underlying conformations and their rates of inter-conversion that is difficult to obtain from ensemble methods(74; 79; 83).

In addition, chemical probing or protection data obtained form techniques such as SHAPE(84) and mutate-and-map(85) can provide valuable information about the various secondary structures populating the nucleic acid free energy landscape, and are increasingly being used in concert with structure prediction and other computational methods to generate atomic resolution structures. These methods will be particularly valuable in characterizing very large RNA structures that are not easily amenable to characterization using techniques such as NMR.

3. Ensemble determination

Thus far, two approaches have been used to construct atomic-resolution ensembles based on experimental measurements. In one approach, the experimental data is directly integrated in the process of generating the conformers, whereas in a second approach, the experimental information in introduced only in a second step after the generation of an initial conformational pool. Both approaches heavily rely on some input from computational modeling or computational force fields to fill the ‘data gap’. Although there are a growing number of studies showing that long-timescale or enhanced MD simulations quantitatively predict experimental data measured in proteins(86; 87), nucleic acid force fields remain underdeveloped and poorly tested. Some of the challenges include proper treatment of strong electrostatic effects and polarization involving the phosophodiester backbone and interactions with metals(88–90). Because of this, it is very important to maximize the amount of data that goes into the ensemble generation and to have rigorous approaches for assessing ensemble accuracy.

3.1 Restrained Molecular Dynamics

Restrained molecular-dynamics provides a way to combine experimental information with molecular dynamic force fields. In this approach, experimental constraints are included as penalty functions or pseudo-energies in the conventional force field, sometimes in combination with additional knowledge-based potentials. Here, the data reproduction is only assessed on average, over the ensemble of conformers determined at each step of the procedure, or sometimes over a time window in a trajectory(91). The exact expression used for the penalty function can vary depending on the specific type of data, but it often assumes a quadratic form (e.g. for RDCs and J-couplings)(92):

$$E=W_j\sum _i{(\langle D_{i,j,\mathit{\text{calc}}}\rangle -D_{i,j\mathit{\text{obs}}})}^2$$ (2)

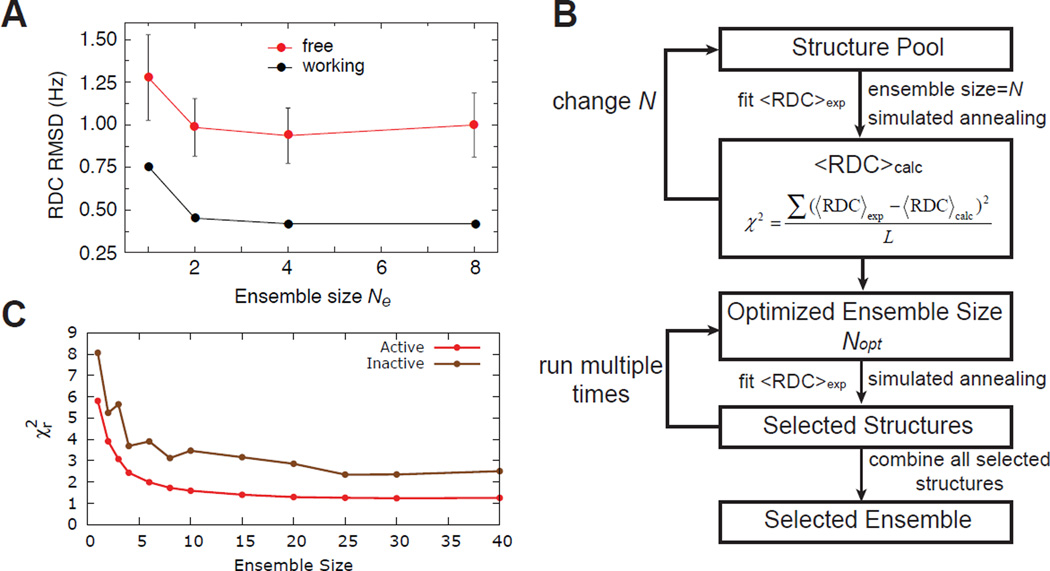
where W_j represents the weight of a given data set j and D_i,j correspond to different experimental data points in this dataset. The detailed protocol of the restrained MD simulation can vary significantly between different studies, with schemes ranking from simulated annealing protocol(93; 94) to also standard MD trajectories. The exact number of conformers in the ensemble can be determined by progressively increasing the number of conformers and monitoring the improvement in the reproduction of active or passive data (vide infra) (Figure 2A).

Figure 2.

Ensemble determination. (A) Typical behaviour of active and passive data reproduction as a function of the number of conformers in the ensemble refinement approach. Adapted from Schwieters and Clore(15) (B) Flow chart for data guided selection of conformers form a pool. (C) Typical behaviour of active and passive data reproduction as a function of the number of conformers in data guided ensemble selection approach. Adapted from Salmon et al.(105)

These approaches have mainly been applied to proteins using a wide range of experimental data(65; 95–97) but also recently to RNA(98). Although not yet implemented for nucleic acids, approaches have been developed to improve sampling in MD simulations in characterizing protein dynamics. Enhanced sampling is particularly important when using NMR RDCs and SAXS data, which have timescale sensitivities that generally exceed those accessible by conventional MD simulations. These approaches include Accelerated Molecular Dynamics (AMD)(99; 100), in which the rates of transition between distinct conformational sub-states is increased by adding a continuous non-negative bias potential to the energy surface, that can be used alone or as a relevant conformational pool for a SAS protocol (see below)(101) and NMR-guided metadynamics, which accelerates conformational sampling using collective variable, including chemical shift reproduction(102).

By introducing an experimental pseudo-potential, this approach can direct the sampling towards conformations that may otherwise not be favored by the force field, but it also remains limited to the use of experimental data that can be efficiently computed during the course of the trajectory. Moreover the number of degree of freedom in the ensemble tend to be larger than the number of experimental restrains, leaving open the possibility of conformational deformation due to overfitting of data. Therefore those procedures are optimal when there is an abundance of experimental data for both defining the number of degrees of freedom and allowing for cross-validation. Another disadvantage is that the introduction of experimental pseudo-potential can in some cases induce non-physical perturbations to the free energy landscape(103).

3.2 Data guided selection of conformers from a pool

An alternative approach involves using the experimental data to guide selection of conformations from a pool that is typically generated using computational methods, such as molecular dynamics simulations. The approach involves two steps (i) generation of a pool of conformations that broadly sample the free energy landscape and (ii) experimental data is used to select a sub-ensemble from the conformational pool that reproduces experimental data(68; 104). This approach is sometimes referred to as ‘sample and select’ (SAS)(104).

The success of SAS-based approaches is critically dependent on having a starting pool that broadly samples the allowed conformations. For nucleic acid applications, starting pools have been generated using standard MD simulations(105; 106), replica exchange molecular dynamics simulations for enhancing sampling(107), and by preforming an exhaustive grid-search when determining inter-helical ensembles involving a small number of structural degrees of freedom(49). Monte-Carlo based approaches have been used in building nucleic acid ensembles but so far have not been used to construct conformational pools that can be used in SAS-based approaches for ensemble determination(108).

In the second step structures are selected from the conformational pool in order to reproduce experimental data. The selection procedure can be accomplished using a variety of search algorithms including simulated annealing(49; 104–106) and genetic algorithms(25; 109; 110). For example, in the simulated annealing approach, N conformers are randomly selected from the MD-generated pool to generate trial sub-ensembles and the agreement between measured and predicted data is computed (Figure 2B). Next, one of the chosen conformers is replaced randomly with another conformer from the pool, and the agreement with measured data re-examined. The newly selected conformer is either accepted or rejected based on the metropolis criteria and several iterations are carried out until convergence is reached, defined as achieving agreement with the measured data that exceeds the experimental error. The ensemble size (N) is then incrementally increased in steps of 1 from N=1 until the convergence criteria is met (Figure 2C). It is worth noting that because the selected conformers are not subjected to further refinements to optimize agreement with experimental data, the number of conformers in an ensemble that are typically required to satisfy measured data generally exceeds that needed in ensemble refinement approaches. This procedure can be repeated hundreds of times, with the family of conformations selected over all runs pooled together to obtain a final ensemble. Recent studies suggest that the SAS approach employing RDCs can be used to capture the statistical weights of dominant conformers in the ensemble (Shan et al in preparation).

One advantage of the SAS approach is that it provides a natural means for evaluating nucleic acid force fields and for identifying potential pitfalls that can be addressed in future developments(105; 111). As nucleic acid force fields improve, we can anticipate that the SAS approach can be extended to include data that is sensitive to timescales and thereby obtain a more complete description of the timescales of inter-conversion. One disadvantage is that in its current implementation, the quality of a determined ensemble is strongly dependent on the conformational pool. For example, if a native conformation is not within the starting pool, it will never be included in any determined ensemble.

3.3 Other approaches for constructing ensembles

Other approaches for constructing ensembles have been developed that seek to assign a statistical weight for various conformers in a pool based on maximum occurrence probability(112) or using Bayesian statistics(113).

4. Assessing accuracy and precision of ensembles

The construction of ensembles using experimental data represents an ill-defined problem because there are usually many different ensembles that can reproduce the experimental observables. It is therefore important to assess uncertainties in the determined ensembles and to integrate these within a statistical framework when interpreting the ensembles.

4.1 Cross validation

Cross-validation is one of the most commonly used approaches for testing the quality of a determined ensemble. Here, a sub-set (typically 10%) of the total experimental data (referred to as ‘passive data’) is omitted form the ensemble determination, and the accuracy of the determined ensembles is assessed by how well it predicts the passive data(114). This provides a straightforward approach for identifying cases where one is over-fitting the data and for testing how well a given set of data can uniquely define an ensemble(15; 105; 109; 110).

An important aspect of cross-validation is the choice of the passive dataset. In general, the passive data can either correspond to data drawn randomly across all different types of data or it can correspond to one type data among many. Regardless of the approach, the active data have to carry the information needed to build a reasonable ensemble. For example, omitting all data points measured for a given residue completely impairs the ability to describe that residue in the ensemble. Likewise, an ensemble determined on the basis of local chemical shift information will, most likely, poorly cross-validate with the global information obtained from SAXS data. On the other hand, choosing passive data that is highly correlated to active data should be avoided, as it might not provide a stringent enough test, for e.g. two sets of highly correlated RDCs data sets (resulting from very similar overall alignments).

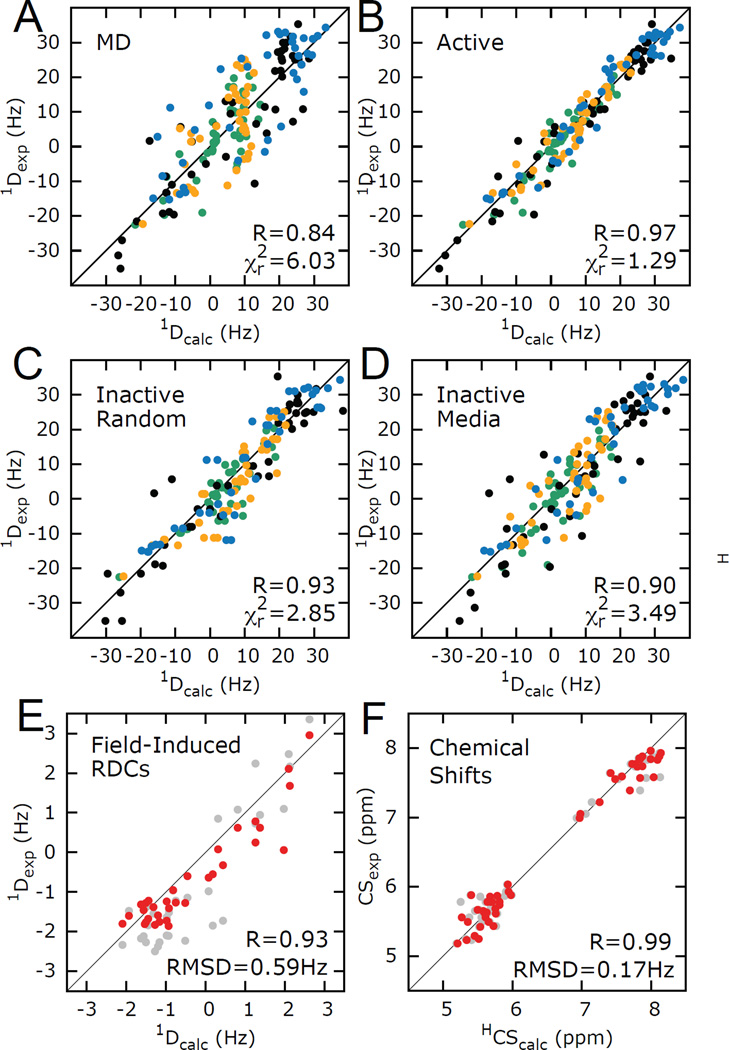
The considerations that enter the choice of passive data are highlighted in a recent study of HIV-1 TAR (Figure 3)(105). Here, four different sets of RDCs were used to construct an ensemble representative of HIV-1 TAR dynamics. Two types of validations were carried out (i) randomly removing a sub-set (~10%) of RDCs from all four datasets (Figure 3D) and (ii) removal of one entire RDC dataset (Figure 3E). The second validation provides a more independent assessment of the quality of the ensemble but also represents a much more stringent test as ~25% of the data had to be removed. Cross-validations were also carried using different types of data (i.e. data other than RDCs measured in ordering media). This includes magnetic field induced RDCs (Figure 3C), which is a good choice for cross-validation as it has the same timescale sensitivity to dynamics as the active data but is obtained though a completely different physical process of alignment and ¹H chemical shifts, which have a distinct dependence on structure (Figure 3F).

Figure 3.

Evaluating HIV-1 TAR ensemble using RDCs and CSs. (A, B) Reproduction of RDCs measured in four differentially elongated TAR RNA constructs (indicated with different colors) using (A) MD starting conformational pool and (B) 20 conformer selected ensemble. (C–F). Cross-validation using (C) randomly selected RDCs (D) individual RDC data sets (E) magnetic field induced RDCs (F) and CSs. In E and F, grey and red data represent reproduction from the starting pool and RDC selected ensemble. Adapted from Salmon et al.(105)

4.2 Tests on synthetic data

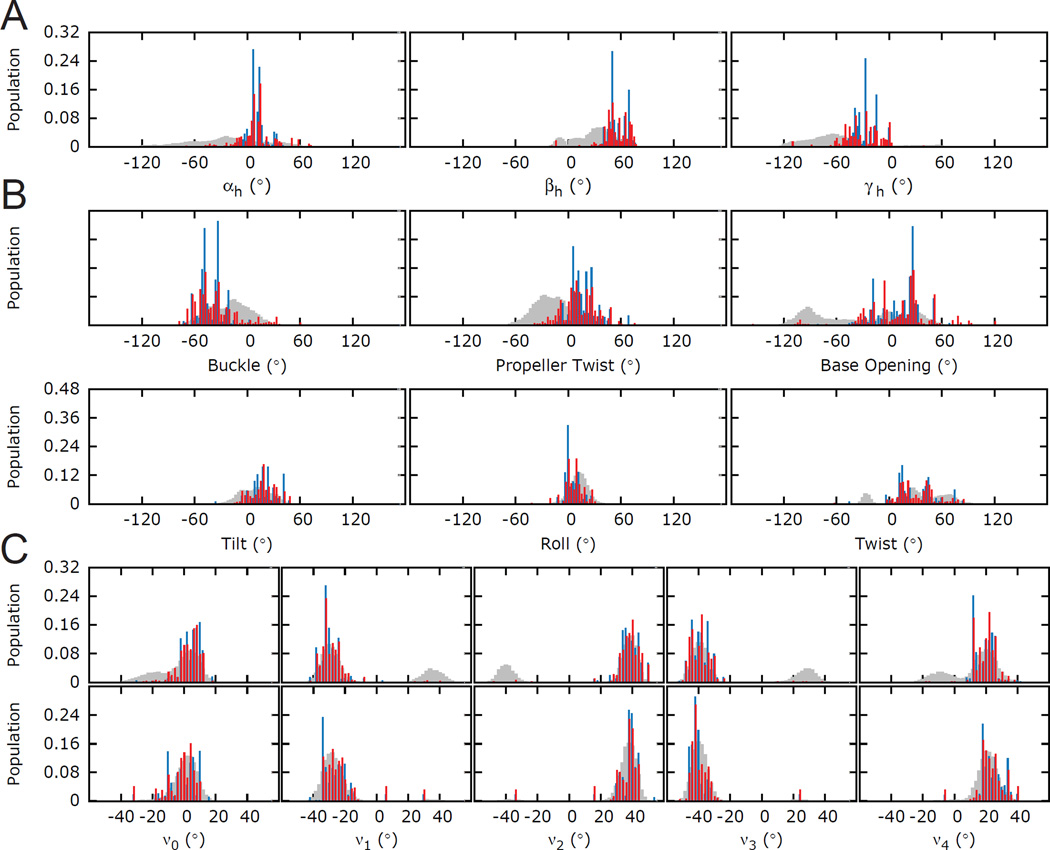
A straightforward approach for assessing the ability of a given experimental data set to determine any aspect of an ensemble is to simply carry out simulations in which the synthetic data, corresponding to the same data that is measured experimentally, is used to reconstruct a known ‘target ensemble’. The target ensemble should represent a reasonable challenge to the data. For example, target ensembles that are simply generated by randomly selecting conformers from a pool present a simpler sampling problem to methods such as SAS as compared to selecting target ensembles that over emphasize lowly populated regions in the conformational pool. In addition the experimental data has to be properly noise corrupted to reflect experimental uncertainties. In this manner, the noise-corrupted data is evaluated for its ability to reproduce the target ensemble (Figure 4). A wide variety of approaches such as the S-matrix and Jensen-Shannon Divergence (JSD) can be used to quantitatively assess the similarity between two ensembles and therefore to assess how well a given set of data reproduces a target ensemble(113; 115–118). The S-matrix is based on the Euclidean distance distribution of pairwise atoms, and is a simplified case of the Wasserstein metric for discrete distribution(116; 117); while JSD is derived from the more general Kullback-Leibler divergence, and is a metric that measures ensemble similarity based on information entropy(113). It should be noted that these metrics do not fully capture ensemble similarities. For example, they are insensitive to the magnitude of the structural differences in non-overlapping ensemble distributions.

Figure 4.

Testing the accuracy of an ensemble determination using simulated data. Distribution of angles in HIV-1 TAR ensemble. (A) Euler angles (α_h,β_h,γ_h) defining the inter-helical orientations(131) (B) intra- and inter-base pair angular parameters for the A22-U40 base-pair (buckle, propeller twist and opening and tilt, roll and twist) and (C) sugar torsion angles (ν₀-ν₄) for the A22-U40 base-pair (top) A22, (bottom) U40. Starting pool, target ensemble, and RDC-selected ensembles are shown in grey, blue and red, respectively. Adapted from Salmon et al.(105)

The approach has the advantage of being generally applicable(98; 105; 109; 110) but tends to underestimate uncertainties in the ensemble that arise due to approximations used in computing the data and in addition does not take into account errors arising due to certain specific conformations are simply not represented in the target pool.

4.3 Monte Carlo Analysis

Monte Carlo analysis is a very general procedure to assess the accuracy and the precision of a given model or parameterization and can therefore be applied to the sampling of a conformational ensemble(109). Here, an experimentally determined ensemble of conformations is typically treated as a target ensemble and used to generate noise-corrupted synthetic data. Next, the target ensemble is determined using several rounds of ensemble determination using synthetic data corresponding to the values back-predicted from the target ensemble and noise-corrupted, independently for each simulations. Although they can be computationally expensive, Monte Carlo simulations can be used in any ensemble determination to estimate the uncertainties in each determined structural parameter(105; 109).

4.4 Bayesian Statistics

Other approaches that utilize Bayesian statistics have been developed to assign weights to conformer in an ensemble and an associated variance that reflects experimental uncertainty(113). Instead of identifying a single value for the population of each conformation, this approach uses Bayesian Weighting formalism to incorporate both experimental data and theoretical prediction to specify a population distribution for each conformation in the ensemble. The uncertainty of the determined population-weighted ensemble can be quantitatively assessed using the posterior expected divergence which can be calculated based on the population distribution alone and was shown to exhibit good correlation with the JSD computed in simulations involving a known target ensemble(113).

5. Applications

Some of the first experimental determinations of macromolecular ensembles, including proteins and DNA, were reported by Clore and co-workers using the restrained MD approach as implemented in the Xplor-NIH software(15). The first application of such ensemble methods to a nucleic acid was for the well-studied Dickerson DNA dodecamer. This study also represents the only current example in which data from multiple sources, including a wide range of NMR parameters (964 RDCs measured in 2 different media, 22 ³¹P RCSAs, 22 ³J_H3’-P couplings, 162 NOEs derived distance restrains) and solution X-ray scattering data were combined in a nucleic acid ensemble determination.

The authors showed that that a single structure representation (N =1) fails to satisfy all measured experimental data, particularly the RDCs and SAXS data. However, an ensemble description with N= 4 or 8 could be used to account for all measured data, as verified through extensive cross-validation analysis against RDC and X-ray scattering data (Figure 2A). Even when ignoring terminal ends, which undergo extensive end-fraying, the ensemble revealed significant fluctuations in helical twist, rise, tilt, roll, and propeller twist which have RMS values ranging from ~3° to 4°, ~0.3 to 0.6 Å, ~5° to 25°, ~9° to 18°, and ~15° to 30°, respectively (Figure 5A). The deoxyribose rings sample a range of sugar puckers from pure C2′-endo to C1′-exo with some evidence of rare C3′-endo forms. In addition, both BI and BII phosphate conformations are observed, with fractional weights that are consistent with empirically predicted values for the different base steps. This study established that DNA structures are not rigid but rather sample distinct conformations along the free energy landscape. These motions are likely to exploited by proteins to increase the specificity of recognition.

Figure 5.

Ensembles of nucleic acids. (A) Ensemble description of the Dickerson DNA dodecamer. Structural representation of the four conformer ensemble and distribution of angular parameters describing the dodecamer base pairs. Angular parameters are plotted on clockfaces where the top corresponds to 0°, the right side to 90°, and the bottom to 180°. The helical rise is plotted on a bar chart with ticks at 1 Å intervals, with the bottom being at 1 Å. The probability increases from blue to green to red. Abbreviations: prop, propeller twist; twist, helical twist. Adapted from Schwieters and Clore(15). (B) Experimentally observed distance distributions between the two gold probes attached to a DNA duplex using Au-SAXS. The gold probes are separated by different numbers of base-pair steps, as indicated by the color-coded numbers. Adapted from Shi et al.(23) (C) SAXS visualization of the ensemble representing the orientation of two helices at various metal concentrations. One helix is depicted in gray while the second is represented using balls that are color-coded according to energetic differences (Red: 0–1 k_BT, orange: 1–2 k_BT, yellow: 2–3 k_BT, blue >3 k_BT). Adapted from Bai et al.(108) (D) Overlay of the 13 free state conformations of SAM-1 riboswitch aptamer domain with helices are represented as cylinders. The bound state is depicted in grey. Adapted from Stoddard et al.(120) (E) Analysis of HIV-1 TAR ensemble. Schematic representation of the three clusters and a proposed ordering for transitioning between conformations with different bend angles. Curved arrows indicate local dynamics. Interactions with helix II are indicated with a dashed line. Structural similarity between (orange) the RDC selected ensemble and (grey) three distinct ligand bound TAR structures. Adapted from Salmon et al.(105)

In a recent study, Harbury and Herschlag(23) employed Au-SAXS interferometry measurements to obtain ensemble distributions for 18 pairwise distances in a model DNA duplex (Figure 5B). The measured average solution structure and microscopic elasticity were in excellent agreement with values derived based on DNA–protein crystal structures and measured by force spectroscopy. However, the measured microscopic torsional rigidity of DNA was much lower than values measured by single-molecule twisting experiments, suggesting that torsional rigidity increases when DNA is stretched. Although the Au-SAXS measurements were not used to explicitly determine an atomic resolution ensemble, efforts are underway to combine distance-derived Au-SAXS measurements with complimentary orientation data derived from RDCs to construct atomic-resolution ensemble of DNA and RNA.

A study by Herschlag, Doniach, and colleagues(108) highlights the power of using SAXS-derived conformational ensembles in testing theories that account for electrostatic interactions with monovalent and divalent ions. The study used a model system consisting of two DNA duplexes tethered by a polyethylene glycol junction to mimic the ‘unfolded state’ of helix-junction-helix RNA motifs. This model system excludes complex interactions such as ion-binding and tertiary contacts that complicate the rigorous evaluation of electrostatic forces. The SAXS scattering profiles measured for this system under different Na⁺ and Mg²⁺ concentrations were used to determine inter-helical conformational ensembles constructed using a Monte Carlo protocol in which the Poisson-Bolzmann theory is utilized to calculate the electrostatic energy. The results showed that Poisson-Bolzmann provides a better description of electrostatic forces involving monovalent ions (e.g. Na⁺) as compared to divalent ions (e.g. Mg²⁺). The results also showed that this simple system samples a wider range of conformations with increasing ionic strength (Figure 5C). While consistent with the expected screening of the repulsive interactions between the two helices by counter ions, these results showed that ions, typically thought to aid folding, tend to actually increase the conformational entropy of the nucleic acid.

Riboswitches are RNA elements that regulate gene expression in response to myriad cellular cues(119). Many riboswitches are integrated into circuits in which they have to undergo large conformational changes efficiently in order to transduce input cellular signals into specific biological outcomes(119). Batey and co-workers(120) used a combination of SAXS, X-ray crystallography, and chemical probing to construct a conformational ensemble for the ligand-sensing aptamer domain of the SAM-I riboswitch in the absence of its cognate ligand. SAXS data measured on the unbound aptamer domain was used to select an ensemble form a conformational pool generated by preforming MD simulations on an X-ray structure of the ligand-bound aptamer(120; 121). A 13-state ensemble constructed in this manner revealed that the sub-domain consisting of P4, the pseudoknot and P2a/b adopts a conformation similar to that seen in the ligand bound state but that the distance between P1 and P3 helices and their orientation relative to P4-PK-P2a/b vary significantly (Figure 5D). These dynamics allow the aptamer to access conformations similar to the bound state, potentially improving the efficiency with which the conformational changes can take place on ligand binding.

RNA often undergoes large changes in conformation involving the reorientation of helical domains across junctions(1). Zhang and Al-Hashimi reported a 3-state ensemble of conformations for the bulge containing HIV-1 TAR using NMR RDCs measured in two distinct elongated samples(49). The ensemble determination was preformed using a SAS type of approach and a grid search over sterically allowed inter-helical conformations as defined by three Euler angle specifying the twist angle about the two helices (α and γ) and the inter-helical bending (β). The authors showed that a static representation of the two helices fails to account for the RDCs and that an ensemble consisting of a minimum of three equally populated states is required. A striking feature of the RDC-derived 3-state ensemble was that the three conformations fell nearly along a straight line in the 3D inter-helix Euler space defining twisting around each helix (α and -γ) and inter-helical bending (β). This hinted to a motional trajectory in which HI and HII bend and twist in a correlated manner. Thus, although the helices undergo large amplitude collective motions (> 90º), they move in a very specific and directional manner. This was a clear sign of ‘directional flexibility’ in RNA and interestingly the 3-state ensemble enveloped many of the known ligand-bound TAR conformations, indicating that on its own, the RNA is capable of sampling a variety of conformations that are stabilized on stabilized on ligand binding. Subsequent studies work by Al-Hashimi(122) and Herschlag(123) showed that the molecular basis for these large and directional inter-helical motions originates in topological constraints (steric and connectivity) which are increasing being show to play essential roles in RNA folding and conformational adaptation(124; 125).

In later studies, the same two sets of RDCs measured in HIV-1 TAR were used to determine atomic-resolution ensembles using the SAS approach and a conformational pool derived from a 50 × 1.6 = 80 ns MD trajectory of HIV-1 TAR(106) computed using the CHARMM package with force field parameter set 27(126). Although some correlation was observed between the measured and predicted RDCs for both EI-TAR and EII-TAR, the deviations (RMSD = 13–16 Hz) were substantially larger than the estimated RDC measurement uncertainty (~4 Hz). However, the simulation time was nowhere near long enough to match the RDC timescale sensitivity of milliseconds, and this failure to predict the RDCs could not be considered to be evidence for a poor force field. Using the SAS approach an ensemble of 20 conformations (N=20) was constructed that satisfies the measured RDCs (RMSD = 4.8 Hz) to near within experimental error(106). The RDC-derived TAR ensemble was qualitatively cross-validated using independent NMR measurements that were not included in the ensemble determination including NOEs and trans-hydrogen bond scalar couplings. It featured very similar correlated variations in the inter-helical bend angle as observed with the 3-state ensemble of TAR but, importantly, it also allowed the visualization of local motions in and around the bulge. The RDC-selected ensemble included conformations that bear strong resemblance to the ligand bound conformations of TAR, including with regards to the details of binding pocket near the bulge, again indicating that intrinsic motions specify the TAR ligand bound conformations(106). In later studies, the dynamic ensemble was targeted using virtual screening yielding new compounds that bind TAR and inhibit HIV replication(127), illustrating one example of a biomedical application involving conformational ensembles.

More recently, Salmon et al(105) developed a modified SAS approach in which PALES is used to back-predict RDCs to construct an ensemble for TAR using four independent sets of RDCs measured in four differentially elongated TAR samples, and a broad pool of conformation derived from a much longer 8.2µs MD trajectory computed on the Anton supercomputer(128) using the updated CHARMM36 force field(126; 129; 130). The agreement between the measured RDCs and values predicted form the entire MD simulation improved, either due to improvements in the force field and/or because of the longer timescales, but it remained significantly larger than experimental uncertainty (Figure 3A). A 20-state ensemble was constructed using SAS that satisfied all measured RDCs to within experimental uncertainty (Figure 3B). The ensemble was validated using extensive tests on simulated data (Figure 3C–F), Monte Carlo simulations and cross-validation analysis involving both RDCs and ¹H experimental chemical shifts (Figure 4).

The high-resolution RDC-derived TAR ensemble in combination with prior data form spin relaxation, made it possible to develop a comprehensive picture of the conformational ensemble that contains timescale information. These data indicate that TAR adopts a family of bent conformations that inter-convert rapidly on the picosecond to microsecond timescales but that there are slower transitions towards more coaxial conformation that require disruption of stacking and hydrogen binding interactions in and around the bulge (Figure 5E). Importantly, this higher resolution ensemble came even closer to within sampling the TAR conformations observed when bound to various ligands, confirming that intrinsic motions specify the ligand bound states (Figure 5E).

6. Conclusion

We have undoubtedly entered the era in which dynamic ensembles rather than static structure of nucleic acids and other biomolecules will be determined at atomic resolution, providing fundamental new insights into their free energy landscapes, and the molecular basis by which they fold and re-structure to carry out functions in living cells. A foundation has been developed for combining different types data with computation in constructing ensembles and for assessing ensemble accuracy culminating in the determination of atomic resolution ensembles for DNA and RNA. There are, however, a number of outstanding challenges and opportunities for the future.

First, there is a need to continue to test and develop nucleic acid force fields. This will require the measurement and dissemination of information rich high quality experimental data that can be used to benchmark simulations. Second, new approaches such as those that rely on the measurements of NMR PRE and relaxation dispersion data need to be further developed and applied to allow detection and 3D structure characterization of short-lived low populated conformers in nucleic acid ensembles, and this information in turn combined with data from other experimental techniques. In this regards, there is also a need for more systematic studies exploring the impact of using samples measured under different experimental conditions and for combining different types of data that might undergo motional averaging at different timescales. Finally, and perhaps most importantly, there is a need to more quantitatively connect the generated ensembles with aspects related to folding and function. Here, we can predict applications in which ensembles make it possible to predict the impact of mutations on the folding stability of nucleic acids or the extent and specificity with which they undergo conformational changes in response to cellular cues.

Summary Points.

1. A wide range of experimental data probing various aspects of structure can also be used to probe conformational ensembles.

2. Different types of experimental data exhibit distinct dependencies on the rates with which conformers in an ensemble inter-convert, complicating their combined use in determining ensembles.

3. Computational methods are often required to fill gaps in experimental data and achieving an optimal balance between experimental and computational input is key for determining ensembles.

4. The determination of ensembles is an under-determined problem that is prone to over interpretation making methods for rigorously assessing the quality of ensembles critically important.

5. Nucleic acids are highly flexible biomolecules that sample a wide range of specific conformations that play important roles in folding and function.

Mini-glossary

Conformational Ensemble

Set of population weighted conformations that are sampled by a biomolecule in solution

Alignment tensor

mathematical entity comprising five independent parameters that describes aspects of partial alignment needed to account for anisotropic NMR interactions

Force field

Empirical values and functions used to describe the potential energy of a system in terms of its degrees of freedom

Chemical Probing

Approach to determine accessibility of residues by measuring their chemical reactivity to externally added agents

Cross-validation

Method to assess quality of a model by evaluating the agreement with data that was omitted in the model generation

Acronyms

SAS

Sample and Select

NMR

Nuclear Magnetic Resonance

SAXS

Small Angle X-Ray Scattering

MD

Molecular Dynamics

RDC

Residual Dipolar Coupling

RCSA

Residual Chemical Shift Anisotropy

CSA

Chemical Shift Anisotropy

CS

Chemical shift

NOE

Nuclear Overhauser Effect