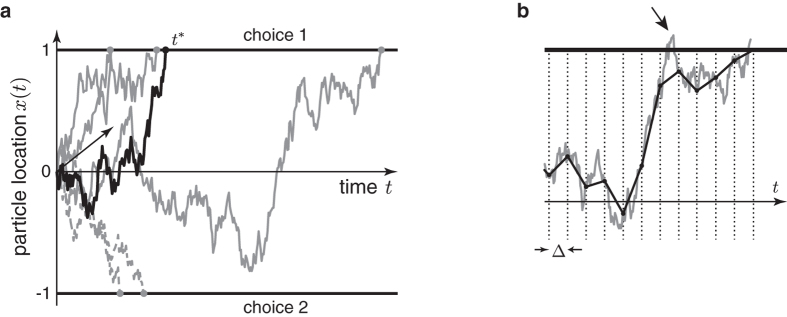
Figure 1. A Wiener diffusion model.

(a) A diffusion model bounded at 1 and −1, with a positive drift (black arrow extending from origin). A choice is triggered as soon as the drifting and diffusion particle, x(t), reaches one of the two boundaries. The black example trajectory triggers choice 1 at time t^*. The stochastic diffusion causes variability in the first-passage times (solid grey trajectories) and choices (dashed grey trajectories). (b) Bias of the Euler-Maruyama method applied to simulating diffusion models, due to discretizing a continuous-time process. This method simulates the stochastic process in discrete time-steps of Δ. The discretized trajectory (black line) might miss temporary excursion of the continuous-time trajectory (grey line) beyond the boundary (black arrow), which causes a bias towards higher first-passage times.