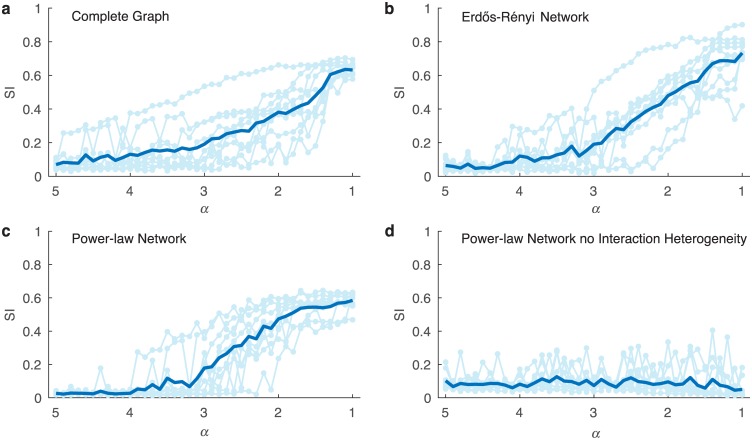
Fig 4. Impact of network structure on the distinctness of community types.

For each type of network structure 10 different Universal Triples (S, A, r) with n = 100 species and q = 500 local communities of size p = 80 were generated with results shown in the lighter color and averaged results shown in bold. (a) Complete graph. Same study as in Fig 2 with α ∈ [5, 1). (b) Erdős-Rényi network (digraph) ${\left[\mathbf{N}\right]}_{ij}\sim \mathcal{N}(0,1)$, ${\left[\mathbf{H}\right]}_{ii}\sim \mathcal{P}\left(\alpha \right)$ where α ∈ (1, 5], Probability [G]_ij = 1 is 0.1, i.e. a mean in(out)-degree of 10, and scaling factor $s=1/\sqrt{10}$. (c) Power-law out-degree network ${\left[\mathbf{N}\right]}_{ij}\sim \mathcal{N}(0,1)$, ${\left[\mathbf{H}\right]}_{ii}\sim \mathcal{P}\left(\alpha \right)$, G is the adjacency matrix for a digraph with out-degree having a power-law distribution $\mathcal{P}\left(\alpha \right)$. The high-degree nodes have the largest interaction scaling. (d) Power-law out-degree network, no interactions strength heterogeneity ${\left[\mathbf{N}\right]}_{ij}\sim \mathcal{N}(0,1)$, H is the identity matrix, G is the adjacency matrix for a digraph with out-degree having a distribution $\mathcal{P}\left(\alpha \right)$. Further details can be found in Materials and Methods.