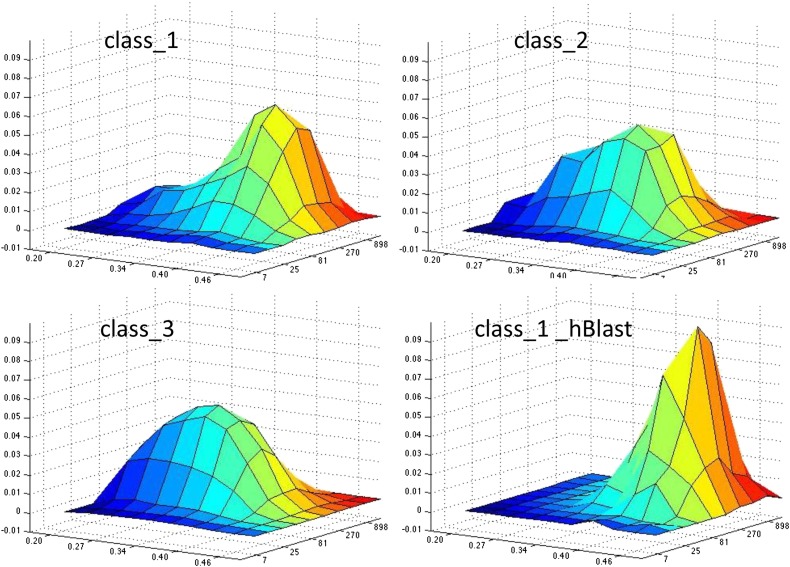
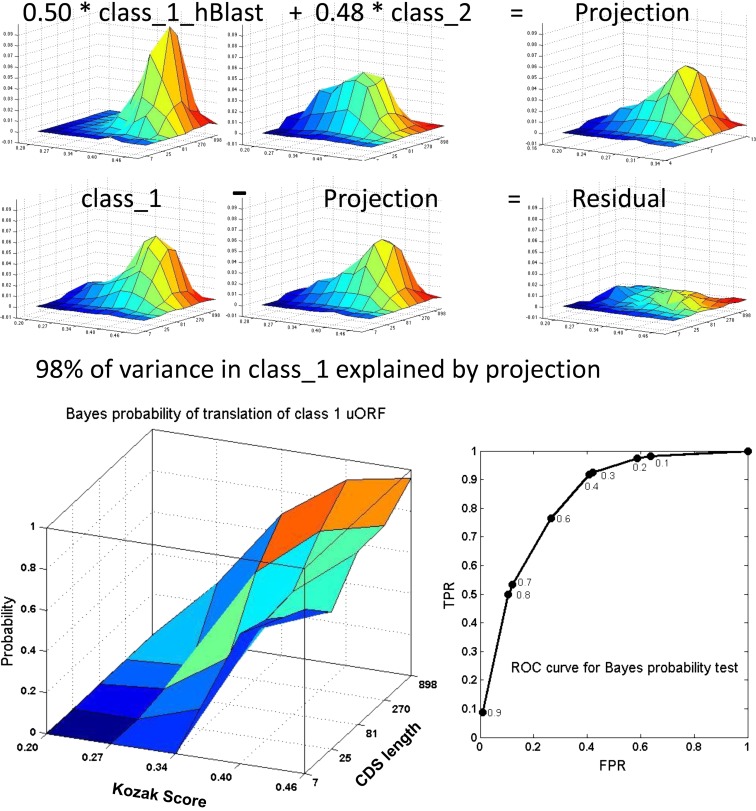
Figure 8.
Two-dimensional accounting for uORF variability. (A) Surface of proportion of uORFs over a two-dimensional grid of Kozak score (exponentiated) and log CDS length. These transformations were chosen because the Kozak score is based on an essentially logarithmic information scale (Figure 3), whereas CDS lengths can be conceptualized as due to exponential decay from finite probability of hitting a stop codon (class 3) or the beginning of the CDS (classes 1 and 2). Classes 2 and 3 have broad peaks with low Kozak scores (left axis) and shorter CDSs (right axis). The high BLASTP-score subclass of class 1 uORFs (lower right) has a sharp peak at high Kozak score and longer CDSs. The complete pool of class 1 uORFs appears heterogeneous, with a peak similar to the high BLASTP subset and a shoulder similar to the distributions of classes 2 and 3. (B) Least-squares accounting for the two-dimensional class 1 uORF distribution as a sum of 0.50 high BLASTP class 1 uORF subset and 0.48 class 2 uORF (matrix calculation as in Figure 4B); 99% of variation is explained. (C) A Bayesian test for translation of class 1 uORFs. Call T the event of translation; K a given Kozak score; L a given length. We want to know P(T | K&L). Bayes theorem says this is equal to: P(K&L | T) × P(T) / [P(K&L | T) × P(T) + P(K&L | ∼T) × P(∼T)]. Assuming ∼50:50 split of translated and untranslated class 1 uORFs (Figure 4C, Figure 7C, and Figure 8B) [i.e., P(T) = P(∼T)], this simplifies to P(T | K&L) = P(K&L | T) / [P(K&L | T) + P(K&L | ∼T)]. K&L specifies a point on the grid; P(K&L | T) is proportional to the height of the high-BLASTP surface over this point, while P(K&L | ∼T) is proportional to the height of the class 2 surface over this point. So this ratio calculated over the whole grid provides a probability estimate. This surface is graphed on the left. On the right is the ROC curve given this surface, for varying cutoffs of nominal Bayesian probability, with the assumption that all translated class 1 uORFs will have sequence properties similar to the high BLASTP score positive training set, while all untranslated class 1 uORFs will be similar to (the presumably untranslated) class 2 uORFs negative training set.