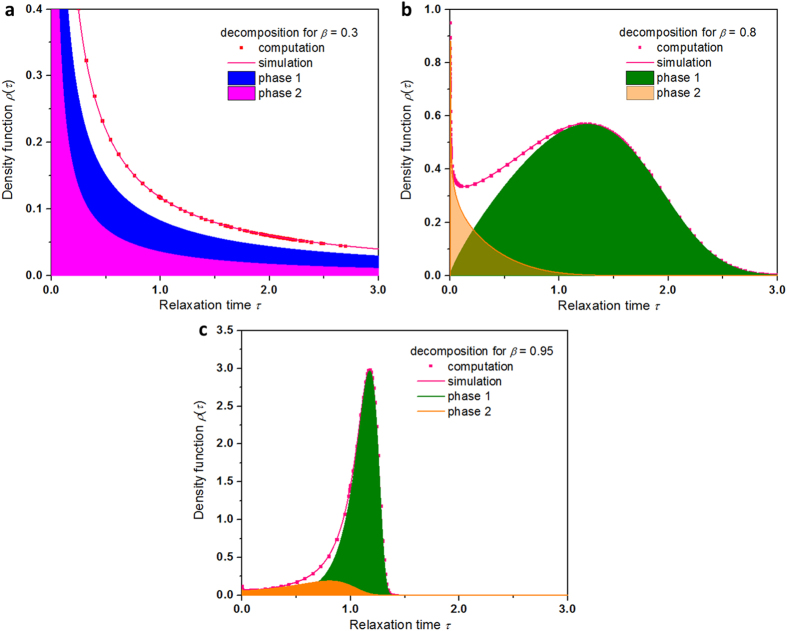
Figure 4. Decomposition analyses of heterogeneity of the probability density function 
for representative values of the stretching parameter β between 0.1 and 0.95.
The probability density function 
shows strong dependence on the stretched exponential 
and consists of two component distributions corresponding to two different dynamic phases. The activities of the dynamic phases are quite dissimilar for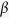 
> 1/2 and 
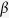< 1/2. The analyses are performed for the same 
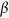. The signs of the symbol-lines represent the computational data points from the equation of 
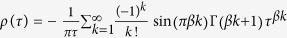(in symbol) and the calculated results based on Eq. 5 in the shadowed regions. The limiting behavior is revealed from the peaking when 
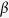approaches 1. a, 
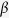= 0.3. b, 
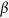= 0.8. c, 
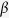= 0.95. The bimodal feature is rapidly diminishing as β approaches 1, with the fast growing magnitude of the major phase against the quick weakening contribution of the minor phase, unveiling the limiting behavior of 
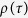as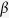 
approaches 1.