Abstract
Terahertz quantum cascade laser sources based on intra-cavity difference-frequency generation are currently the only room-temperature mass-producible diode-laser-like emitters of coherent 1–6 THz radiation. Device performance has improved dramatically over the past few years to reach milliwatt-level power output and broad tuning from 1.2 to 5.9 THz, all at room-temperature. Terahertz output in these sources originates from intersubband optical nonlinearity in the laser active region. Here we report the first comprehensive spectroscopic study of the optical nonlinearity and investigate its dependence on the mid-infrared pump frequencies. Our work shows that the terahertz generation efficiency can vary by a factor of 2 or greater depending on the spectral position of the mid-infrared pumps for a fixed THz difference-frequency. We have also measured for the first time the linewidth for transitions between the lower quantum cascade laser states, which is critical for determining terahertz nonlinearity and predicting optical loss in quantum cascade laser waveguides.
The terahertz (THz) spectral range (0.3–10 THz) has a proven potential for a variety of applications, such as spectroscopy, communications, and security screening1,2,3,4. Room-temperature THz sources analogous to diode lasers in the near-infrared/visible or quantum cascade lasers (QCL) in the mid-infrared (mid-IR), i.e. electrically-pumped, compact, widely-tunable, and suitable for low-cost production, are highly desired for feasible and inexpensive THz systems. Despite significant development of THz QCLs over the past 12 years5,6,7,8, their operating temperatures are limited to 200 K for pulsed operation9 and 130 K for continuous-wave (CW) operation10.
THz sources based on intra-cavity difference-frequency generation (DFG) in dual-wavelength mid-IR QCLs11,12,13,14,15,16,17,18,19,20 are currently the only electrically-pumped mass-producible monolithic semiconductor laser sources that can operate at room temperature in 1–6 THz region. With the introduction of waveguides designed for Cherenkov phase-matching12,13, these devices, referred to as THz DFG-QCLs, have achieved dramatic improvement in power and tuning bandwidth. A single ridge-waveguide THz DFG-QCL can now output nearly 2 mW of THz peak power in pulsed mode and microwatt-level THz power in CW mode, all at room temperature14,15. When integrated in an external cavity setup, these devices can provide widely-tunable narrowband THz emission from 1 to 6 THz at room temperature13,16. A variety of monolithic electronically-tunable THz DFG-QCL sources were also demonstrated at room temperature17,18,19.
Terahertz generation in THz DFG-QCLs is produced via the nonlinear mixing of the two mid-IR pump fields generated in the QCL active region. The active region is also designed to have resonant optical nonlinearity χ(2) associated with transitions between the upper laser states and the manifold of the lower laser states as shown in Fig. 1(a,b)11,12,13,14,15,16,17,18,19,20,21,20. Terahertz power output (WTHz) scales with the product of mid-IR pump powers (W1 and W2) and the square of the magnitude of χ(2) 11,12,13,14,15,16,17,18,19,20:
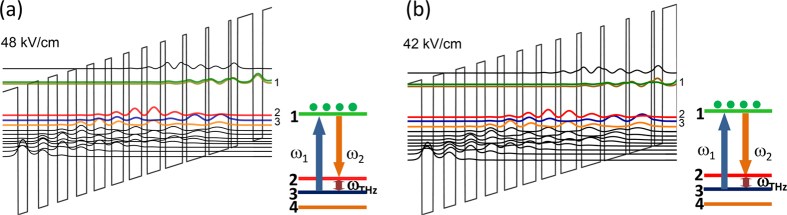
Figure 1. Active region band structure of two-stack active region design under applied bias computed using a Schrödinger solver26.
(a) Conduction band diagram of one period of λ = 8.5 μm active region at 48 kV cm−1 bias field, close to the rollover point. Inset: schematic diagram showing the DFG process between the electron states in this structure. Transition dipole matrix elements and energy spacing between states 1, 2, and 3 are computed to be z12 = 2.2 nm, z13 = 1.9 nm, z23 = 8.0 nm, E12 = 135 meV, E13 = 154 meV. (b) Conduction band diagram of one period of λ = 9.5 μm active region at 42 kV cm−1 bias field, close to the rollover point. Inset: schematic diagram showing the DFG process between the electron states in this structure. Transition dipole matrix elements and energy spacing between states 1, 2, and 3 are computed to be: z12 = 2.3 nm, z13 = 2.2 nm, z23 = 9.0 nm, E12 = 121 meV, E13 = 137 meV.
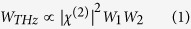 |
The ability to accurately predict and maximize χ(2) in the active region is critical for further advancement of THz DFG-QCL technology.
Referring to the energy state labelling shown in Fig. 1 and keeping only resonant terms, the quantum mechanical expression for χ(2) for THz DFG is given as20.
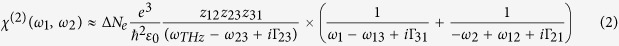 |
where ω1 and ω2 are the frequencies of mid-IR pumps, ωTHz = ω1 − ω2 is THz difference-frequency, ΔNe is the population inversion density, 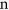 and
and 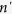 are the lower state levels (levels 2,3, and other lower laser levels shown in Fig. 1), ezij, ωij, and Γij are the transition dipole moments, transition frequency, and transition linewidth factor between states
are the lower state levels (levels 2,3, and other lower laser levels shown in Fig. 1), ezij, ωij, and Γij are the transition dipole moments, transition frequency, and transition linewidth factor between states  and
and 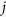 . Equation (2) shows that χ(2) has a strong 2-dimensional (2D) dependence on the mid-IR pump frequencies. However, no work has been performed so far to experimentally measure the dependence of χ(2) on ω1 and ω2 in THz DFG-QCLs. The linewidth factor Γ23 for THz transitions between the lower laser states has also not been experimentally quantified. Determining the linewidth factor Γ23 is critical for improving the modeling accuracy of χ(2) and optical loss in the lower laser levels structure of QCLs. We note that it is nearly impossible to measure Γ23 using linear absorption techniques because both states 2 and 3 are designed to be quickly depopulated under QCL operating bias.
. Equation (2) shows that χ(2) has a strong 2-dimensional (2D) dependence on the mid-IR pump frequencies. However, no work has been performed so far to experimentally measure the dependence of χ(2) on ω1 and ω2 in THz DFG-QCLs. The linewidth factor Γ23 for THz transitions between the lower laser states has also not been experimentally quantified. Determining the linewidth factor Γ23 is critical for improving the modeling accuracy of χ(2) and optical loss in the lower laser levels structure of QCLs. We note that it is nearly impossible to measure Γ23 using linear absorption techniques because both states 2 and 3 are designed to be quickly depopulated under QCL operating bias.
Here we report the results of the first 2D nonlinear spectroscopic study of THz generation in DFG-QCLs. We obtain the values for linewidth Γ23 and experimentally show that the THz generation efficiency at a fixed THz frequency (ωTHz = ω1 − ω2) for a specific applied bias field can vary by a factor of 2 or more, depending on the choice of ω1 and ω2. Our results and the 2D spectroscopic technique presented here are expected to play a crucial role in the analysis and future optimization of the performance of the only room-temperature semiconductor-laser-like sources of THz radiation.
Results
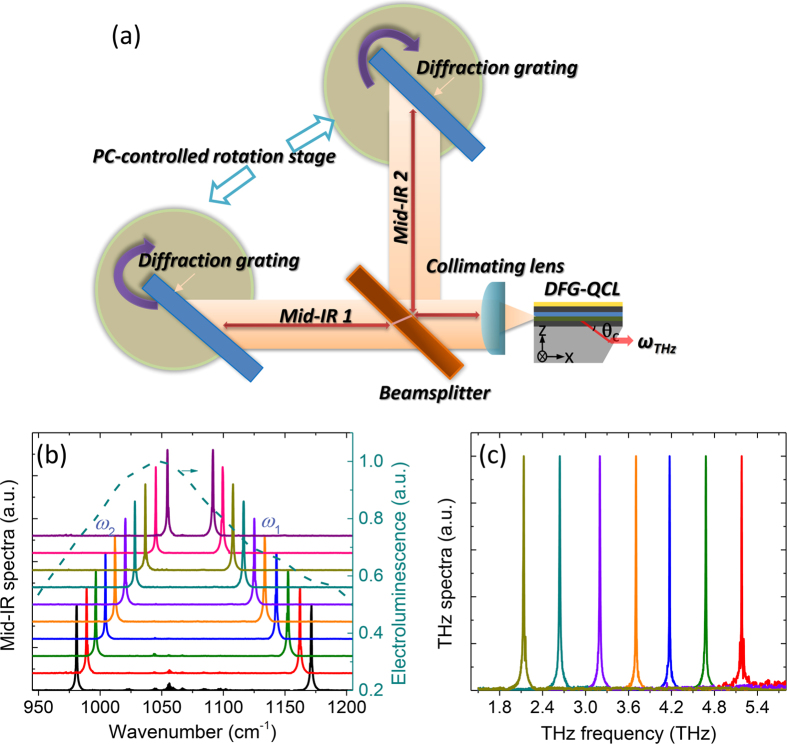
The experimental setup used in this work is presented in Fig. 2(a) and additional details are given in Methods. We performed independent tuning of the two mid-IR pumps using a dual-diffraction-grating external cavity (EC) setup. The positions of the diffraction gratings were computer controlled. Our setup may be viewed as an extension of Littrow-type external cavity setup used for mid-IR QCLs21,22. It is also similar to a dual-grating EC setup used previously for dual-color tuning of near-infrared diode lasers23. Cherenkov THz DFG emission from the device was collected through a 30-degree polished device substrate facet as shown schematically in Fig. 2(a) 12,15. Terahertz power measurements were performed in a N2-purged environment with a calibrated liquid-helium cooled bolometer. Individual mid-IR pump powers were spectrally separated using interference filters and measured with a calibrated thermopile detector. All measurements were performed at room temperature using 50 ns current pulses at a 50 kHz repetition frequency. Further details of the experimental setup are provided in Methods.
Figure 2. Details of the laser tuning setup.
(a) Schematic of the dual-grating Littrow-type external cavity used in this work. The back facets of the laser chips are coated with a two-layer anti-reflection coating (AR) as described in ref. 16. The collimating lens is an AR-coated aspheric lens with a focal length of 1.87 mm and a numerical aperture of 0.85. The non-polarizing beam splitter is made of ZnSe and transmits (reflects) approximately 50% of the incident light. Two gold-coated 150 grooves per mm diffraction gratings are used to provide frequency-tunable feedback for the two mid-IR pump frequencies (ω1 and ω2) independently. (b) Mid-IR emission spectra of a THz DFG-QCL in the setup depicted in (a) for several different grating positions. In this example one diffraction grating tunes mid-IR pump frequency ω2 from 980 cm−1 to 1054 cm−1 and the other diffraction grating tunes mid-IR pump frequency ω1 from 1091 cm−1 to 1170 cm−1. The electroluminescence spectrum of the laser material is shown with a dashed line. (c) Selected THz emission spectra of the device recorded for the same diffraction grating positions as in (b).
Cherenkov THz DFG-QCL chips used in our work were identical to devices reported in ref. 13. The laser structure was grown by molecular beam epitaxy on a 350-μm-thick semi-insulating InP substrate. The laser active region was comprised of 33 repetitions of the bandstructure shown in Fig. 1(a) designed to have a gain peak at λ = 8.5 μm followed by 33 repetitions of the bandstructure shown in Fig. 1(b) that was designed to have a gain peak at λ = 9.5 μm. This dual-stack active region is designed to provide a broad gain bandwidth for mid-IR pump tuning with a difference-frequency as high as ~6 THz13,16. Devices were fabricated into 14 to 32 μm wide ridge-waveguide lasers using a dry etching process. A lateral current extraction scheme was used due to the non-conductive nature of the semi-insulating InP substrate12,13. Further details of the device structure are provided in Methods. The results discussed below are all obtained with a 22-μm-wide, 1.7-mm-long device; however, similar results were obtained with devices of other dimensions.
Selected mid-IR tuning spectra from the THz DFG-QCL in the EC setup are shown in Fig. 2(b) for different grating positions. The corresponding THz emission spectra of the device are shown in Fig. 2(c). For the 2D spectroscopy results presented in Fig. 3, the frequency of mid-IR pump 1 (ω1) was varied between 1091 cm−1 to 1151 cm−1 and the frequency of pump 2 (ω2) was varied, independently, between 981 cm−1 to 1052 cm−1. THz DFG frequency corresponds to the frequency separation between the two mid-IR pumps (ωTHz = ω1 − ω2) and could be tuned from 1.17 THz (39 cm−1) to 5.10 THz (170 cm−1).
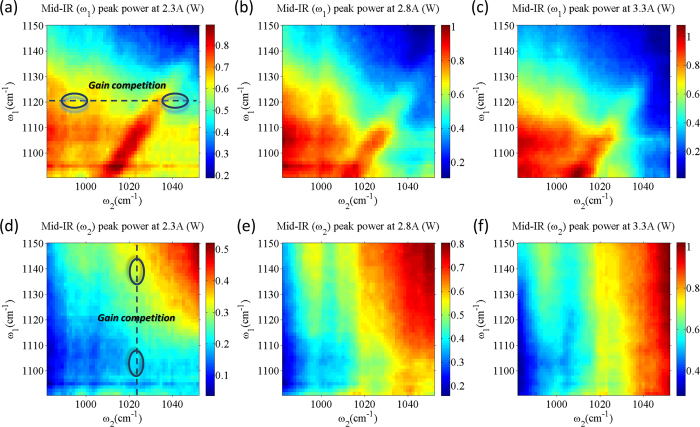
Figure 3. Mid-IR peak power output (in watts) as a function of mid-IR pump frequencies ω1 and ω2.
The pump frequencies ω1 and ω2 are selected by the angle of two external diffraction gratings. Panels (a–c) show the peak power output of ω1 pump at pump currents of 2.3 A, 2.8 A and 3.3 A, respectively. Panels (d–f) show the peak power output of ω2 pump at pump currents of 2.3 A, 2.8 A and 3.3 A, respectively.
The peak power of mid-IR pump 1 and pump 2 as a function of pump frequencies selected by external gratings is shown in Fig. 3(a–f), respectively. Measurements were performed at three different currents of 2.3 A, 2.8 A, and 3.3 A (current density of 6.2 kA/cm2, 7.5 kA/cm2, and 8.8 kA/cm2), corresponding to near laser threshold, mid dynamic range, and near laser rollover, respectively. The effect of gain competition between the two mid-IR pumps can be observed: in Fig. 3(a), the intensity of pump 1 decreases as the frequency of pump 2 is tuned towards ω1, and in Fig. 3(d), the intensity of pump 2 decreases as the frequency of pump 1 is tuned towards ω2. Similar gain competition effects are seen at higher bias currents in Fig. 3(b,c,e,f). Gain competition is an intrinsic effect in all dual-color semiconductor lasers and has been reported previously for THz DFG-QCLs16,24,25. It can be seen in Fig. 3(a,d) that dual-color mid-IR lasing is possible for a wide range of ω1 and ω2 frequencies despite gain competition. The balance of mid-IR pump powers can be managed by controlling the individual round-trip gain and/or loss for the two pumps19. We further note that even with gain competition, both mid-IR pumps operate in the TM00 mode, as confirmed by far field measurements, due to spatial filtering of EC feedback at device aperture.
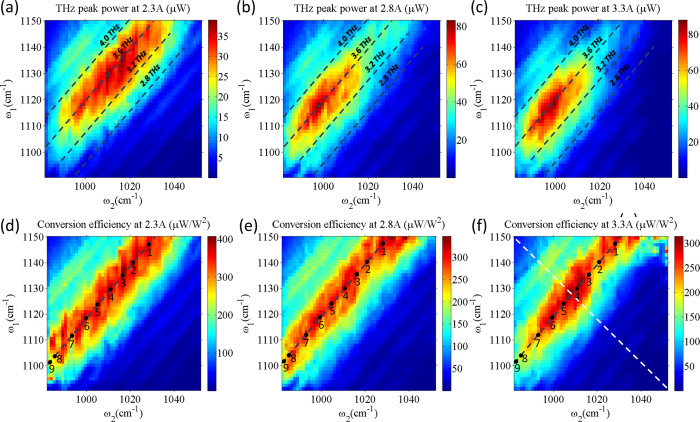
The dependence of THz peak power on the two mid-IR pump frequencies is shown in Fig. 4(a–c). Similar to data in Fig. 3(a–f), measurements for the data in Fig. 4(a–c) were performed at three different pump currents of 2.3 A, 2.8 A, and 3.3 A (current density of 6.2 kA/cm2, 7.5 kA/cm2 and 8.8 kA/cm2). Figure 4(d–f) shows the mid-IR-to-THz conversion efficiency η(ω1, ω2) for the three different bias currents, defined as the ratio of THz power output from a device to the product of mid-IR pump powers,
Figure 4. THz DFG performance of the device.
Panels (a–c) show the THz peak power output (in μW) of the device at pump currents of 2.3 A, 2.8 A and 3.3 A, respectively, as a function of mid-IR pump frequencies ω1 and ω2. Panels (d–f) show mid-IR-to-THz conversion efficiency (in μW/W2) of the device at pump currents of 2.3 A, 2.8 A and 3.3 A, respectively, as a function of mid-IR pump frequencies ω1 and ω2. Black dashed lines in all panels correspond to the sets of data points with the constant values of THz DFG frequency at 2.8, 3.2, 3.6 and 4.0 THz. Points labelled with numbers indicate frequencies of the two mid-IR pumps for which we performed more detailed measurements of THz power output as a function of mid-IR pump powers as shown in Fig. 5. White dashed line in (f) indicates the set of data points used to determine Γ23 linewidth as shown in Fig. 6.
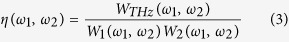 |
where W1(ω1, ω2) is the power of mid-IR pump 1 shown in Fig. 3(a–c), W2(ω1, ω2) is the power of mid-IR pump 2 shown in Fig. 3(d–f), and WTHz(ω1, ω2) is the THz output power shown in Fig. 4(a–c). The dashed lines in Fig. 4(a–c) represent positions of the same THz difference frequency of 2.8 THz, 3.2 THz, 3.6 THz and 4.0 THz. It can be seen in Fig. 4(d–f) that the mid-IR-to-THz conversion efficiency profile as a function of ω1 and ω2 does not stay constant and the maximum mid-IR-to-THz conversion efficiency is achieved for different combinations of mid-IR pump frequencies as the device bias changes. This is true even if the THz difference-frequency stays the same.
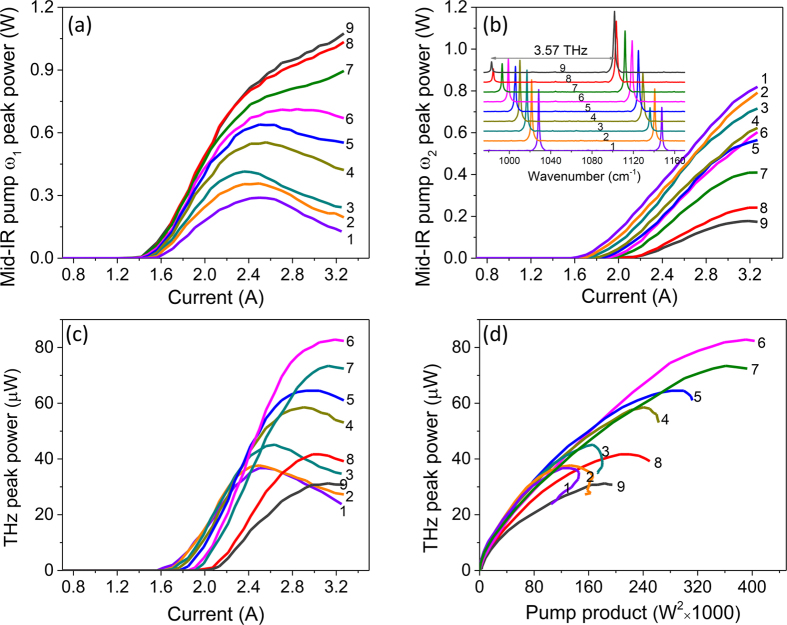
To illustrate this point further, we performed mid-IR and THz light-output-current characterization of the device at 9 different combinations of ω1 − ω2 that fixed the THz difference-frequency at 3.57 THz. These ω1 and ω2 combinations are indicated with black dots in Fig. 4(d–f). Figure 5(a,b) show the power of mid-IR pump 1 and pump 2 as a function of current through the device for the 9 different combinations of ω1 − ω2; the emission spectra at a pump current of 3.3 A for the same 9 combinations of ω1 − ω2 are shown in the inset of Fig. 5(b). Figure 5(c) shows the THz light-output-current characteristics of the device producing 3.57 THz difference-frequency and Fig. 5(d) plots THz power output as a function of the product of the two mid-IR pump powers, obtained from the data shown in Fig. 5(a,b), for the same combinations of ω1 and ω2. From Eq. (1), a linear dependence between the THz power output and mid-IR pump power product is expected under the assumption of a constant χ(2). However, Fig. 5(d) shows that this is not the case experimentally. Moreover, Fig. 5(d) shows that the mid-IR-to-THz conversion efficiency can vary by a factor of 2 or more depending on the choice of mid-IR pump frequencies for fixed 3.57 THz difference-frequency emission. To explain the results, we need to consider the dependence of χ(2) on the mid-IR pumps frequencies and the bias voltage. Indeed, Eq. (2) shows that as transition energies between subbands 1, 2 and 3 change with applied bias, the value of χ(2) and its dependence on ω1 and ω2 may vary significantly.
Figure 5. Device performance at a fixed difference-frequency of 3.57 THz with 9 different combinations of ω1 and ω2 (indicated with 9 black dots in Fig. 4(d–f)).
Panels (a,b) show the power of mid-IR pump ω1 and pump ω2, respectively, as a function of current through the device. Inset in (b) shows the mid-IR emission spectra at pump current of 3.3 A. Panel (c) shows THz light-output-current characteristics of the device and (d) shows THz power output as a function of the product of the mid-IR pump powers, for 9 different combinations of ω1 and ω2.
Discussion
To provide qualitative explanation of the results in Fig. 5, we computed the bandstructures of the two stacks (shown in Fig. 1) that comprise the active region for different bias voltages: near the threshold alignment point, in the middle of the dynamic range, and near the rollover point (specifically, at 41 kV cm−1, 44 kV cm−1, and 47 kV cm−1, respectively, for stack 1 and 46 kV cm−1, 49 kV cm−1, and 52 kV cm−1, respectively, for stack 2). Transition energies and transition dipole moments between states 1, 2, and 3 were then computed from the bandstructures26 and Eq. (2) was used to calculate χ(2)(ω1, ω2) in each of the active region stack. In this calculation, the transition linewidth between upper and lower laser states Γ21 and Γ31 were assumed to be 15 meV for both stacks based on electroluminescence measurements13, while the linewidth Γ23 for the transition between lower laser states was varied from 2 meV to 8 meV. We have also assumed a constant ΔNe = 8.5 × 1014 cm−3 in accordance to the value used for similar devices in ref. 13. We note that the data in Fig. 5(a,b) shows that threshold current density (and, correspondingly, ΔNe) in our device may change by up to ~20% depending on the spectral position of ω1 and ω2 pumps. Considering the qualitative nature of our theoretical model, we have neglected the variation in ΔNe to simplify calculations. More detailed analysis of the dependence of χ(2)(ω1, ω2) on pump frequencies and threshold gain should also include electron transport and the resultant non-uniform electric field distribution (band bending) across the active region. Such analysis can be performed using Monte-Carlo simulations27,28 in future work.
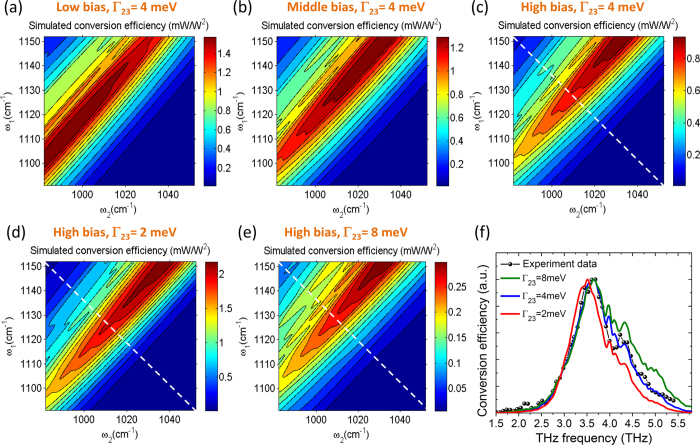
To simulate the mid-IR-to-THz conversion efficiency for different values of ω1 and ω2 at the three different bias points, we used a slab-waveguide approximation that treats the Cherenkov THz emission as a leaky waveguide mode. The procedure is described in detail in ref. 29 for Cherenkov second harmonic generation and is applied to THz DFG-QCL modeling in ref. 13. The results are shown in Fig. 6(a–c) assuming Γ23 = 4 meV. Theoretical dependence of conversion efficiency on ω1 and ω2 is in good qualitative agreement with the experimental measurements in Fig. 4(d–f), although experimental values of conversion efficiencies are approximately 3 times lower than expected. As discussed in Methods, THz power measurements were not corrected for collection efficiency owing to challenges in operating the THz power measurement setup (mid-IR powers were corrected for collection efficiency). Relatively low collection efficiency of THz radiation may explain the discrepancy between theory and experiment. Limitations of the slab-waveguide model and uncertainties in materials parameters may also contribute to the discrepancy between theory and experiment. Both theory and experiment show conversion efficiency for DFG at 3.57 THz drops by a factor of 1.5 as the bias field increases. This happens because the values of transition energies and transition dipole moments in Eq. (2) vary with the bias field, which leads to changes in the value of χ(2) and the mid-IR-to-THz conversion efficiency. Also, at low-to-moderate bias fields, both experimental data and theory show nearly constant conversion efficiency for different combinations of mid-IR pump frequencies as long as the THz difference-frequency stays the same. At higher bias, both experimental data and theory shows that THz DFG conversion efficiency is maximized at specific combinations of ω1 and ω2, around 1130–1150 cm−1 and 1010–1030 cm−1, respectively. Given the simplicity of our model, the agreement is remarkable. The experimental and theoretical results demonstrate that careful selection of the spectral position of mid-IR pumps is critically important for optimization of THz DFG-QCL performance.
Figure 6.
Calculated mid-IR-to-THz conversion efficiency for the tested devices as a function of mid-IR pump frequencies ω1 and ω2 assuming Γ23 = 4 meV near threshold (a), in the middle of dynamic range (b) and near the rollover point (c–e) Calculated mid-IR-to-THz conversion efficiency for tested devices as a function of mid-IR pump frequencies close to the rollover point and assuming Γ23 = 2 meV (d) and Γ23 = 8 meV (e,f) Cross section data comparison between theory and experiment. Black circles are experimental data taken along white dashed line in Fig. 4(f); red, blue and green lines are the theoretical values taken along white dashed line in panels (d,c,e). Theoretical data with the linewidth factor Γ23 = 4 meV provides the best match to the experimental data.
Finally, we used our 2D DFG spectroscopic analysis to deduce, for the first time, the approximate value of the intersubband transition linewidth Γ23 between lower laser states of the bound-to-continuum QCL active region. We note that it is virtually impossible to measure Γ23 by linear absorption spectroscopy since the electron population difference between these lower laser states is very small. In Fig. 6(c–e), we show simulated conversion efficiency at bias fields near the rollover point as a function of ω1 and ω2 assuming Γ23 ≈ 4 meV, 2 meV, and 8 meV for both QCL stacks, respectively. The best agreement between simulations and experimental measurements shown in Fig. 4(f) is achieved for Γ23 ≈ 4 meV. To clarify this point further, we compare the experimental and theoretical data points taken along the white dashed lines in Fig. 4(f) and Fig. 6(c–e). The results are shown in Fig. 6(f). The theoretical curve with Γ23 = 4 meV clearly provides the best fit with the experimental data. In particular, our theoretical model predicts a factor of 11, 6, and 3 drop in mid-IR-to-THz conversion efficiency at 5 THz compared to 3.6 THz for Γ23 = 2 meV, 4 meV, and 8 meV, respectively. The drop in mid-IR-to-THz conversion efficiency measured experimentally is approximately 6.5. A value of Γ23 = 4 meV is in a reasonable agreement with the 2Γ = 2.8 meV electroluminescence linewidth measured at 10 K in a lattice matched InGaAs/AlInAs/InP 3.6 THz QCL30 and a linewidth of 2Γ = 2.5 meV measured at ~10 K in a passive GaAs/Al0.33Ga0.67As quantum well structure at 4.7 THz31, considering the expected linewidth increase at room temperature.
In summary, we have performed a comprehensive investigation of the 2D spectroscopic dependence of THz DFG in QCLs with Cherenkov phase-matching on the positions of mid-IR pump frequencies. Our results demonstrate that mid-IR-to-THz conversion efficiency in Cherenkov THz DFG-QCLs may vary by a factor of 2 for the same THz DFG frequency, depending on the spectral position of the mid-IR pumps. We have also experimentally deduced the linewidth of THz transitions between the lower laser states, which is critical for the accurate modeling of χ(2) and understanding the optical loss in the lower laser level structure of mid-IR QCLs. The 2D spectroscopic technique presented here is expected to play a crucial role in the analysis and future optimization in the performance of THz DFG-QCLs.
Methods
Device growth and fabrication
The laser structure was grown by molecular beam epitaxy (MBE) on a 350-μm-thick semi-insulating InP substrate. The growth commenced with a 200-nm-thick InGaAs current injection layer (Si,7 × 1017 cm−3), followed by a 3-μm-thick InP lower cladding (Si,1.5 × 1016 cm−3). The active region made with an InGaAs/InAlAs heterostructure lattice-matched to InP was grown next. It comprised of 33 repetitions of the bandstructure shown in Fig. 1(a) designed to have a gain peak at λ = 8.5 μm followed by 33 repetitions of the bandstructure shown in Fig. 1(b) that was designed to have a gain peak at λ = 9.5 μm. The layer sequence of the λ = 9.5 μm design, is 39/22/8/60/9/59/10/52/13/43/14/38/15/36/16/34/19/33/23/32/25/32/29/31, and for the λ = 8.5 μm design is 43/18/7/55/9/53/11/48/14/37/15/35/16/33/18/31/20/29/24/29/26/27/30/27, where the layer thicknesses are in angstroms, bold numbers indicate barriers, and underlined numbers indicate regions doped with Si to n = 2 × 1017 cm−3. The top cladding layer consisted of 3-μm-thick InP (Si, 1.5 × 1016 cm−3), followed by a 100-nm-thick InP layer (Si, 3 × 1018 cm−3) and terminated with a 10-nm-thick InGaAs contact layer (Si, 2 × 1019 cm−3). Samples were processed into 22-μm-wide dry-etched ridge waveguides via inductive plasma etching. The sidewalls of the ridges were insulated with a 400-nm-thick layer of silicon nitride, followed by Ti/Au (15 nm/800 nm) contact metallization. Given the insulating nature of the substrate, a lateral contact current injection scheme was employed. The wafer was cleaved into laser bars approximately 1-2 mm long. The 350-μm-thick InP substrate associated with the THz exit facet of the device was mechanically polished at a 30 degree angle for the THz Cherenkov wave out-coupling. Special care was taken to ensure that the laser waveguide facets are unaffected by polishing. Devices were then Indium soldered epi-side up onto copper holders and wire bonded.
External cavity setup
The dual-grating experimental setup is shown in Fig. 2(a). The back facets of the Cherenkov THz DFG-QCL chips are coated with a two-layer anti-reflection (AR) coating using YF3 and ZnSe designed to have a minimum reflection around the middle of the gain bandwidth of the device16. An AR-coated aspheric lens with a focal length of 1.87 mm and a numerical aperture of 0.85 is used to collimate the mid-IR emission from the back facet of the laser. The collimated mid-IR beam is then split by a 50/50 ZnSe beam splitter and directed to two diffraction gratings (gold coated, 150 grooves mm−1) placed on two computer-controlled rotation stages. The gratings are used to provide frequency-tunable feedback for two mid-IR pump frequencies (ω1 and ω2) independently.
Power and spectral measurements
Power measurements are done in a N2-purged environment using two parabolic mirrors: one parabolic mirror with a two inch focal length is used to collect and collimate light from the device and the other parabolic mirror with a six inch focal length is used to refocus the collimated beam onto a thermopile detector for mid-IR power measurements or a calibrated silicon bolometer for THz power measurements. Optical filters are used to spectrally separate the two mid-IR pumps. Mid-IR power is corrected for 70% collection efficiency of the setup. THz power measurements are not corrected for collection efficiency. Mid-IR and THz emission spectra of devices are measured with Nicolet iS50R Fourier-transform infrared spectrometer (FTIR) equipped with a deuterated L-alanine doped triglycine sulphate detector (DTGS) for mid-IR measurements and a helium-cooled silicon bolometer for terahertz measurements at a spectral resolution of 0.25 cm−1.
Additional Information
How to cite this article: Jiang, Y. et al. Spectroscopic Study of Terahertz Generation in Mid-Infrared Quantum Cascade Lasers. Sci. Rep. 6, 21169; doi: 10.1038/srep21169 (2016).
Acknowledgments
This work was supported in part by the National Science Foundation grants number ECCS-1150449 (CAREER), ECCS-1408511, and IIP-1448707 (SBIR). Walter Schottky Institute group acknowledges financial support from the excellence cluster “Nano Initiative Munich (NIM)”. Sample fabrication was carried out in the Microelectronics Research Center at the University of Texas at Austin, which is a member of the National Nanotechnology Coordinated Infrastructure.
Footnotes
Author Contributions Y.J. designed, constructed and characterized the demonstrated 2D THz-DFG QCL system; K.V. contributed to the bandstructure design; S.J. helped the characterization; A.J. and J.H.K. helped with fabrication. F.D. and G.B. carried out the QCL growth; M.C.A. supervised the efforts of the Munich team; M.B. conceived and supervised the overall project. Y.J., K.V. and M.B. wrote the manuscript.
References
- Ferguson B. & Zhang X.-C. Materials for terahertz science and technology. Nat. Mater. 1, 26–33 (2002). [DOI] [PubMed] [Google Scholar]
- Tonouchi M. Cutting-edge terahertz technology. Nat. Photon. 1, 97–105 (2007). [Google Scholar]
- Jepsen P. U., Cooke D. G. & Koch M. Terahertz spectroscopy and imaging – Modern techniques and applications. Laser Photon. Rev. 5, 124–166 (2011). [Google Scholar]
- Dean P. et al. Terahertz imaging using quantum cascade lasers—a review of systems and applications. J. Phys. D: Appl. Phys. 47, 374008 (2014). [Google Scholar]
- Kohler R. et al. Terahertz semiconductor-heterostructure laser. Nature 417, 156–159 (2002). [DOI] [PubMed] [Google Scholar]
- Williams B. S. Terahertz quantum-cascade lasers. Nat. Photon. 1, 517–525 (2007). [Google Scholar]
- Sirtori C., Barbieri S. & Colombelli R. Wave engineering with THz quantum cascade lasers. Nat. Photon. 7, 691–701 (2013). [Google Scholar]
- Vitiello M. S., Scalari G., Williams B. & De Natale P. Quantum cascade lasers: 20 years of challenges. Opt. Express 23, 5167–5182 (2015). [DOI] [PubMed] [Google Scholar]
- Fathololoumi S. et al. Terahertz quantum cascade lasers operating up to ~ 200 K with optimized oscillator strength and improved injection tunneling. Opt. Express 20, 3866–3876 (2012). [DOI] [PubMed] [Google Scholar]
- Wienold M. et al. High-temperature, continuous-wave operation of terahertz quantum-cascade lasers with metal-metal waveguides and third-order distributed feedback. Opt. Express 22, 3334–3348 (2014). [DOI] [PubMed] [Google Scholar]
- Belkin M. A. et al. Terahertz quantum-cascade-laser source based on intracavity difference-frequency generation. Nat. Photon. 1, 288–292 (2007). [Google Scholar]
- Vijayraghavan K. et al. Terahertz sources based on Čerenkov difference-frequency generation in quantum cascade lasers. Appl. Phys. Lett. 100, 251104 (2012). [Google Scholar]
- Vijayraghavan K. et al. Broadly tunable terahertz generation in mid-infrared quantum cascade lasers. Nat. Commun. 4, 2020 (2013). [DOI] [PubMed] [Google Scholar]
- Razeghi M. et al. Quantum cascade lasers: from tool to product. Opt. Express 23, 8462–8475 (2015). [DOI] [PubMed] [Google Scholar]
- Lu Q. Y., Bandyopadhyay N., Slivken S., Bai Y. & Razeghi M. Continuous operation of a monolithic semiconductor terahertz source at room temperature. Appl. Phys. Lett. 104, 221105 (2014). [Google Scholar]
- Jiang Y. et al. External cavity terahertz quantum cascade laser sources based on intra-cavity frequency mixing with 1.2–5.9 THz tuning range. J. Opt. 16, 094002 (2014). [Google Scholar]
- Jung S. et al. Broadly tunable monolithic room-temperature terahertz quantum cascade laser sources. Nat. Commun. 5, 4267 (2014). [DOI] [PubMed] [Google Scholar]
- Lu Q. Y., Slivken S., Bandyopadhyay N., Bai Y. & Razeghi M. Widely tunable room temperature semiconductor terahertz source. Appl. Phys. Lett. 105, 201102 (2014). [Google Scholar]
- Jiang A. et al. Widely tunable terahertz source based on intra-cavity frequency mixing in quantum cascade laser arrays. Appl. Phys. Lett. 106, 261107 (2015). [Google Scholar]
- Belkin M. A. et al. Room temperature terahertz quantum cascade laser source based on intracavity difference-frequency generation. Appl. Phys. Lett. 92, 201101 (2008). [Google Scholar]
- Maulini R., Beck M., Faist J. & Gini E. Broadband tuning of external cavity bound-to-continuum quantum-cascade lasers. Appl. Phys. Lett. 84, 1659–1661 (2004). [Google Scholar]
- Wysocki G. et al. Widely tunable mode-hop free external cavity quantum cascade lasers for high resolution spectroscopy and chemical sensing. Appl. Phys. B 92, 305–311 (2008). [Google Scholar]
- Chi M., Jensen O. B. & Petersen P. M. High-power dual-wavelength external-cavity diode laser based on tapered amplifier with tunable terahertz frequency difference. Opt. Lett. 36, 2626–2628 (2011). [DOI] [PubMed] [Google Scholar]
- Geiser M. et al. Gain competition in dual wavelength quantum cascade lasers. Opt. Express 18, 9900–9908 (2010). [DOI] [PubMed] [Google Scholar]
- Vijayraghavan K. et al. THz Difference-Frequency Generation in MOVPE-Grown Quantum Cascade Lasers. IEEE Photon. Technol. Lett. 26, 391–394 (2014). [Google Scholar]
- Faist J. Quantum cascade lasers. (Oxford University Press, 2013). [Google Scholar]
- Jirauschek C., Matyas A., Lugli P. & Amann M.-C. Monte Carlo study of terahertz difference frequency generation in quantum cascade lasers. Opt. Express 21, 6180–6185 (2013). [DOI] [PubMed] [Google Scholar]
- Jirauschek C., Okeil H. & Lugli P. Monte Carlo analysis of the terahertz difference frequency generation susceptibility in quantum cascade laser structures. Opt. Express 23, 1670–1678 (2015). [DOI] [PubMed] [Google Scholar]
- Hashizume N. et al. Theoretical analysis of Cerenkov-type optical second-harmonic generation in slab waveguides. IEEE J. Quantum Electron. 28, 1798–1815 (1992). [Google Scholar]
- Ajili L., Scalari G., Hoyler N., Giovannini M. & Faist J. InGaAs–AlInAs/InP terahertz quantum cascade laser. Appl. Phys. Lett. 87, 141107 (2005). [Google Scholar]
- Sirtori C., Capasso F., Faist J., Pfeiffer L. N. & West K. W. Far-infrared generation by doubly resonant difference frequency mixing in a coupled quantum well two-dimensional electron gas system. Appl. Phys. Lett. 65, 445–447 (1994). [Google Scholar]