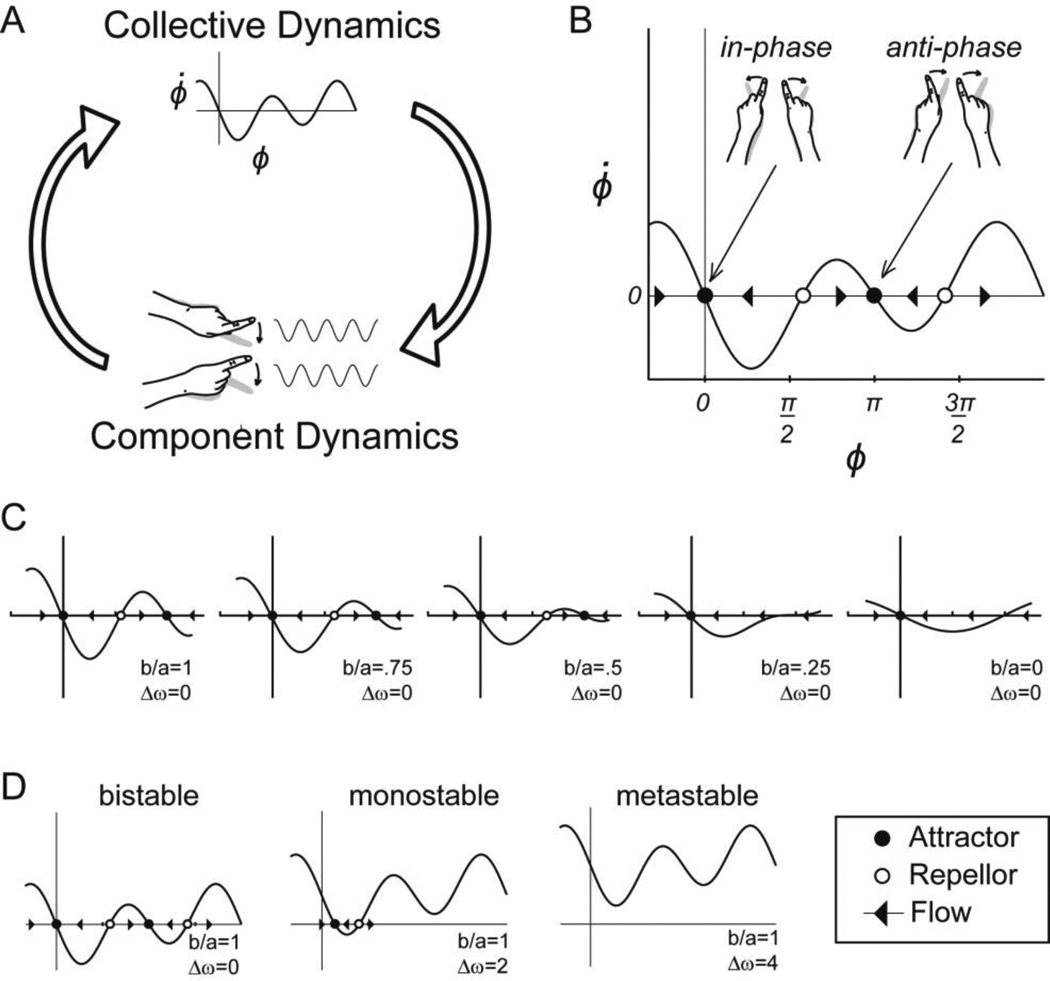
Figure 2.

The dynamics of rhythmically coordinated finger movements. A) The coordinated action of muscles acting to rhythmically oscillate the left and right index fingers is found to give rise to the collective dynamics of equation 1. B) The collective variable relative phase (ϕ) captures the coordinated state of the components. For example, in-phase coordination (ϕ=0) identifies a collective state in which identical muscles of the left and right hand are used synchronously. The dynamics (i.e. change over time) of ϕ reveals stable fixed points (●) to which the collective state of the system is attracted, and unstable fixed points (○) from which the collective state of the system is repelled. The direction of change is shown with arrows depicting the direction of flow. C) Changes in strength of coupling between left and right fingers modelled with the parameter b/a in equation 1 give result in the loss of a fixed point attractor as b/a in varied from 1 to 0. D) Dynamical regimes observed as a function of difference in the natural frequencies of component oscillators captured by the parameter (Δω).