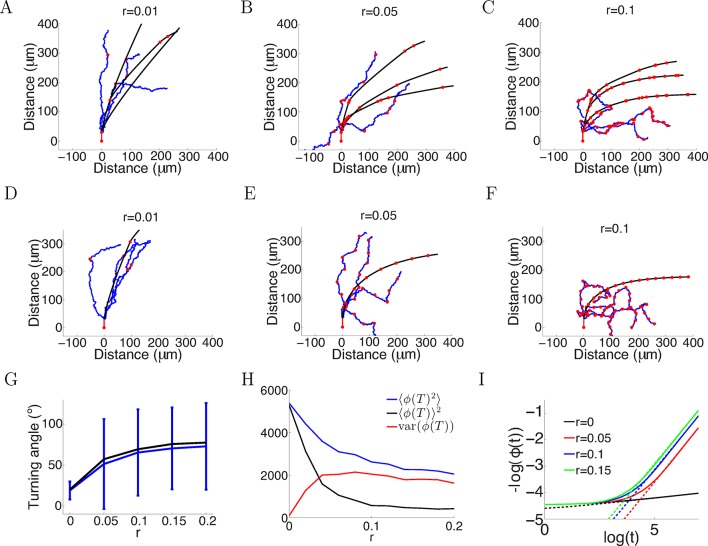
Figure 14. More variability with more anchor points.

(A–C) Trajectories of growth cones with probability of putting down a new anchor r= 0.01, 0.05, 0.1 at each timestep and the same parameters as Figure 2A (a = 1, b = 0.1, T = 150 timesteps). The black plots are without noise in the bearing changes, the blue plots are with noise $\xi ~N(0,\pi /4)$ radians in the bearing changes and the red dots are the anchor points. More anchor points lead to higher variability but also stronger turning. The means and standard deviations of turning angles and the values for the noiseless versus the noisy case in brackets for r = 0.01, 0.05, 0.1 are 32 ± 9° (30 ± 36°), 55 ± 8° (49 ± 57°) and 67 ± 5° (60 ± 56°), respectively. (D–F) Trajectories of growth cones with the same rate of putting down new anchor points as A-C but at regular intervals. The means and standard deviations of turning angles and the values for the noiseless versus the noisy case in brackets are 27° (24 ± 17°), 57° (54 ± 51°), 69° (66 ± 51°). (G) The means and standard deviations of turning angles after 150 timesteps as a function of the anchoring rate at regular intervals in the noiseless and the noisy case. (H) The mean square of the final growth cone angle (in degrees) $⟨\varphi {\left(T\right)}^2⟩$ for different anchoring rates r after 150 steps. $⟨\varphi {\left(T\right)}^2⟩$ is the sum of the bias term ${⟨\varphi \left(T\right)⟩}^2$ and the variance term var($\varphi \left(T\right)$). Although more anchor points add more variance to the final angle (red curve), they achieve stronger turning $\varphi \left(T\right)\approx 0$ (black curve). (I) The evolution of $\varphi \left(t\right)$ over time, for the case of anchoring at regular intervals and no noise in the movement (ξ = 0). With more anchor points, $\varphi \left(t\right)$ also follows the power law but with steeper slope, meaning that $\varphi \left(t\right)\to 0$ at a faster rate than the case without anchor points.

DOI: http://dx.doi.org/10.7554/eLife.12248.029