CpGFilter: model-based CpG probe filtering with replicates for epigenome-wide association studies

Abstract

Summary: The development of the Infinium HumanMethylation450 BeadChip enables epigenome-wide association studies at a reduced cost. One observation of the 450K data is that many CpG sites the beadchip interrogates have very large measurement errors. Including these noisy CpGs will decrease the statistical power of detecting relevant associations due to multiple testing correction. We propose to use intra-class correlation coefficient (ICC), which characterizes the relative contribution of the biological variability to the total variability, to filter CpGs when technical replicates are available. We estimate the ICC based on a linear mixed effects model by pooling all the samples instead of using the technical replicates only. An ultra-fast algorithm has been developed to address the computational complexity and CpG filtering can be completed in minutes on a desktop computer for a 450K data set of over 1000 samples. Our method is very flexible and can accommodate any replicate design. Simulations and a real data application demonstrate that our whole-sample ICC method performs better than replicate-sample ICC or variance-based method.

Availability and implementation: CpGFilter is implemented in R and publicly available under CRAN via the R package ‘CpGFilter’.

Contact: chen.jun2@mayo.edu or xlin@hsph.harvard.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Recent advances in genomic technologies have enabled researchers to conduct large-scale studies of human disease-associated epigenetic variation, specifically variation in DNA methylation. Such epigenome-wide association studies (EWAS) have helped elucidate the non-genetic determinants of human disease (Rakyan et al., 2011). The Illumina Infinium HumanMethylation450 Beadchip, which interrogates the methylation level of more than 450K CpG sites throughout the human genome, has been increasingly popular in large-scale EWAS due to its good genome coverage, high reproducibility and lower cost (Sandoval et al., 2011). One observation of the 450K data is that many CpGs have relatively larger technical variability compared with their biological variability, which are results of either large absolute technical variability (the methylation level cannot be measured accurately) or lower biological variability (many CpGs are constitutively methylated or unmethylated). These CpGs are less informative and including these CpGs will reduce the statistical power to discover relevant CpG sites by unnecessarily increasing the number of statistical tests. Hence, CpG filtering could potentially boost statistical power for underpowered studies. Traditional variance-based CpG filter is based on the total variability, which is the sum of the biological variability (signal) and technical variability (noise). However, we are more interested in retaining CpGs with relatively large biological variability instead of total variability. As with any hybridization-based array technology, CpG probes differ in their technical variability, possibly due to inexact probe sequence match, cross-hybridization and local secondary structures (Price et al., 2013). Therefore, large total variability does not necessarily reflect large biological variability. Without technical replicates, the assessment of technical variability is difficult and we can only rely on the total variability to filter CpGs. Fortunately, most EWAS have included some technical replicates to assess various sources of batch effects. We can therefore use these replicates to assess technical variability. We propose to use intra-class correlation coefficient (ICC), which is defined as the ratio of biological variability to total variability, to filter CpG probes (Donner et al., 1980). We extend technical replicate-based method by Meng et al. (2010) and Bose et al. (2014) and estimate ICC using a linear mixed effects model (LMM) by pooling all samples including the unreplicated ones. Compared with the method using technical replicates only, our method can result in more efficient ICC estimate since the unreplicated samples provide significant amount of information about the biological variability. Our method can accommodate any type of replicate design including unbalanced design. We have implemented an ultra-fast algorithm to fit LMM in linear computational time and the algorithm is highly scalable.

2 Model

Suppose we have m independent biological samples measuring the methylation of p CpGs. Assume each biological sample replicates $n_i(i=1,\dots ,m)$ times, totaling $n={\displaystyle {\sum }_{i=1}^m{n}_i}$ samples. Note in most studies, the majority of the samples are not replicated and the majority of $n_i=1$. Before ICC estimation, we recommend that data normalization and batch correction be performed to remove systematic technical variability. Denote y_ij as the methylation M-value of a given CpG for ith biological sample and its jth technical replicate. We model y_ij using an LMM

$$y_{\mathrm{ij}}=\mu +{\xi }_i+{\epsilon }_{\mathrm{ij}}\hspace{1em}i=1,\dots ,m\hspace{0.5em}\mathrm{and}\hspace{0.5em}\mathrm{j=1,}\dots ,n_i$$ (1)

where ${\mathrm{ϵ}}_{\mathrm{ij}}\sim N(0,{\sigma }_{\mathrm{ϵ}}^2)$ and ${\xi }_i\sim N(0,{\sigma }_{\xi }^2)$ represent technical and biological variability respectively. Denote $y_i=(y_{i1},\dots ,y_{i{n}_i})$ and $Y={(y_1,y_2,\dots ,y_m)}^T$, we then have

$$Y\sim \mathrm{MVN}\left(\mathbf{\mu },V\right),$$

with the mean $\mathit{\mu }={(\mu ,\mu ,\cdots ,\mu )}^T$ and the covariance matrix V

$$V={\sigma }^2{\left(\begin{array}{cccc}{A}_1& & & \\ & A_2& & \\ & & \ddots & \\ & & & A_m\end{array}\right)}_{n\times n}{A}_i={\left(\begin{array}{cccc}1& \rho & \cdots & \rho \\ \rho & 1& \cdots & \rho \\ ⋮& ⋮& \ddots & ⋮\\ \rho & \rho & \cdots & 1\end{array}\right)}_{n_i\times n_i,}$$

where ${\sigma }^2={\sigma }_{\mathrm{ϵ}}^2+{\sigma }_{\xi }^2$ is the total variance and $\rho ={\sigma }_{\xi }^2/({\sigma }_{\mathrm{ϵ}}^2+{\sigma }_{\xi }^2)$ is the ICC. When ${\sigma }_{\mathrm{ϵ}}^2$ is the same for all CpGs, the filtering procedure based on the total variance is the same as that based on ICC. However, as in all array-based technologies, different probes have different measurement error levels, and ICC is generally a more appropriate measure than total variance. Fitting a mixed effects model with existing general-purpose algorithms is computationally intensive and is not scalable with the ever increasing sample size and CpG sites for genome-wide association studies. The major contribution of this paper is therefore the development of an ultra-fast algorithm based on maximum likelihood estimation, utilizing the special structure of the covariance matrix (block-diagonality and compound symmetry structure). The computational complexity is O(np) and scalable with the sample size and CpG number. The detailed algorithm is included in the Supplementary Note S1.

3 Results

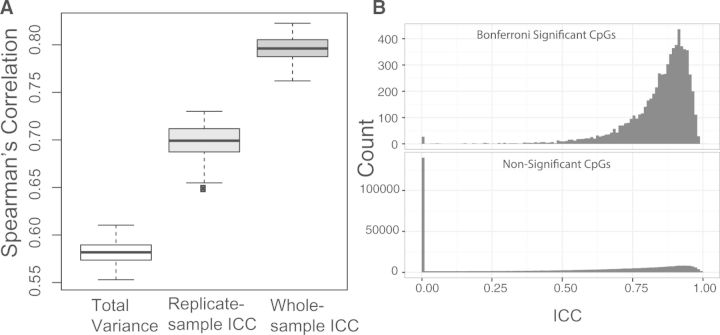
We compare our whole-sample ICC method to the replicate-sample ICC method by Bose et al. (2014) as well as the total variance-based method using simulations. We simulate 1000 CpGs and 1000 independent samples, among which 10 samples are replicated twice. Let ${\sigma }_{\xi }\sim \text{Uniform}(0.5,8.0)$ and ${\sigma }_{\mathrm{ϵ}}\sim \text{Uniform}(0.25,2.0)$. We then simulate the methylation M-values based on the model (1) and rank these CpGs based on ICC or variance after applying the three alternatives. We calculate the Spearman correlation between the resulted ranking and the ranking based on the simulated true ρ’s, which is assumed to be the best. Simulations are repeated 100 times. Figure 1A shows our whole-sample ICC method produces invariably better ranking than the other two methods (median correlation 0.80 vs. 0.70 and 0.58). We next study the effects of ICC-based CpG filtering on the type I error and power of association tests using realistic simulations (Supplementary Note S2). CpGs with small ICCs will have no or little chance of showing significance, and removing these CpGs will enrich signals against a background of noise. As expected, using Bonferroni correction and false discovery rate control for multiple comparison correction, the proposed method has achieved better power than the replicate-sample ICC method, while controlling the type I error at the desired level. Simulation also suggests at least six technical replicate pairs to achieve good results.

Fig. 1.

Performance of whole-sample ICC method. (A) Comparison of CpG ranking performance of three competing methods based on simulated data. (B) The distribution of whole-sample ICCs for (Bonferroni) significant and non-significant CpGs based on real data

We apply our method to a cleaned 450K dataset of 482 985 methylation sites from buffy coat leukocytes of 559 males and 10 technical replicate pairs from the Normative Aging Study (Marioni et al., 2015). We conduct an epigenome-wide cross-sectional analysis of age (median 72, range 55–100 years) based on a linear model, adjusting for subject characteristics, estimated cell type proportions and technical covariates. Strict Bonferroni correction is used to select ‘significant’ CpG sites. Clearly, these sites are dramatically enriched in large ICC values (Fig. 1B). We see that 96.7% of the sites associated with age come from those with an ICC greater than the median (0.55). We also see 138 562 sites with an estimated ICC of zero, indicating much larger technical variability (measurement error) compared with their biological variability. In comparison with the ICC method, if we had only used the sites with total variance above the median, we would have captured only 93% of the sites associated with age in the full analysis (Supplementary Fig. S1). In general, an ICC cutoff of around 0.5 provides a good trade-off between loss of potential significant CpG sites due to filtering and gain of power due to reduction of multiple testing burden (Supplementary Fig. S1).

Funding

This work was supported by NCI R37 CA76404, NCI P01 CA134294, NCI R35 CA197449, NIEHS R01 ES015172, NIEHS R01 ES021733, K99 ES023450 and Gerstner Family Career Development Award.

Conflict of Interest: none declared.