Direct observation of Σ7 domain boundary core structure in magnetic skyrmion lattice

Advanced electron microscopy reveals a unique structural relaxation mechanism in a magnetic skyrmion domain boundary core.

Abstract

Skyrmions are topologically protected nanoscale magnetic spin entities in helical magnets. They behave like particles and tend to form hexagonal close-packed lattices, like atoms, as their stable structure. Domain boundaries in skyrmion lattices are considered to be important as they affect the dynamic properties of magnetic skyrmions. However, little is known about the fine structure of such skyrmion domain boundaries. We use differential phase contrast scanning transmission electron microscopy to directly visualize skyrmion domain boundaries in FeGe_1−xSi_x induced by the influence of an “edge” of a crystal grain. Similar to hexagonal close-packed atomic lattices, we find the formation of skyrmion “Σ7” domain boundary, whose orientation relationship is predicted by the coincidence site lattice theory to be geometrically stable. On the contrary, the skyrmion domain boundary core structure shows a very different structure relaxation mode. Individual skyrmions can flexibly change their size and shape to accommodate local coordination changes and free volumes formed at the domain boundary cores. Although atomic rearrangement is a common structural relaxation mode in crystalline grain boundaries, skyrmions show very unique and thus different responses to such local lattice disorders.

INTRODUCTION

Electronic and mechanical properties of modern functional materials are strongly affected by grain boundaries (1). The structures of grain boundaries are influenced by various factors: the crystallographic orientations of the two adjacent grains, the characteristics of chemical bonding at the interfaces, and the segregation of impurity atoms into grain boundaries to form unique atomic-scale structures and thus change the properties (2, 3). Furthermore, the formation of amorphous grain boundary sometimes complicates the situation (4). With all of these influences, grain boundary structure is too complicated to be addressed in a simple manner. However, as a first-order approximation, the effects of crystallographic orientation are successfully analyzed using the coincidence site lattice (CSL) theory (5, 6). The theory proved to be powerful in predicting stable orientation relationships and grain boundary plane orientations between two adjacent crystals.

On the other hand, many atom-like physical entities other than actual atoms interact with each other to form unique ordered structures. Magnetic structures in helical magnets, such as MnSi and Fe_1−xCo_xSi, have recently been found to exhibit hexagonal lattice (7, 8) in response to external magnetic field and temperature. The atom-like physical entity in these unique structures is called “skyrmion,” which was first theoretically introduced in quantum field theory to explain the stability of elementary particles (9). Skyrmion in magnetic materials was first observed in real space using Lorentz transmission electron microscopy (LTEM) (10). It was soon confirmed that such magnetic skyrmion actually behaves just like atoms, forming various ordered lattice structures and topological defects within them. For example, magnetic twin boundary, inversion boundary, and dislocations in hexagonal skyrmion lattice were reported in several publications (10–12). Domain boundary formation in skyrmion lattice (interface between two skyrmion lattice domains with different orientations) in FeGe_1−xSi_x (13) and in Cu₂OSeO₃ (14) has been reported recently. However, the core structures and stabilization mechanisms of such domain boundaries have not been studied in detail so far.

Real-space visualization techniques are critically important in investigating the behavior of nanoscale magnetic structures such as skyrmions. Scanning probe microscopes, such as a magnetic force microscope (MFM) (15) or spin-polarized scanning tunneling microscope (SP-STM) (16), are powerful techniques used to analyze not only in-plane but also out-of-plane components of magnetization at the surface of bulk specimens. However, these methods cannot be used to investigate the very fine magnetic structure because of the resolution limitation in MFM and the high requirement for sample surface in SP-STM. Moreover, they are limited to the observation of the top surface of bulk specimens. On the other hand, conventional LTEM combined with a phase retrieval technique based on transport of intensity equation (17) can visualize magnetic structures inside thin-film specimens. In addition, electron holography can also be used to quantitatively evaluate projected two-dimensional magnetization (18). However, these methods need elaborate and time-consuming post-image analysis to extract the magnetic structure information from the original images. On the other hand, in recent years, aberration-corrected scanning transmission electron microscopy (STEM) has become a very powerful tool not only for directly imaging atomic-scale structures with subangstrom spatial resolution (19) but also for directly imaging electromagnetic structures at high resolution in combination with the differential phase contrast (DPC) imaging mode, which was originally introduced by Dekkers and de Lang (20). In this imaging mode, a quadrant-segmented detector is commonly used to analyze the amplitude and direction of the Lorentz deflection of a focused electron beam; thus, various magnetic structures of nanometer dimensions can be directly imaged (21, 22). Very recently, a highly sensitive segmented annular all-field (SAAF) detector combined with aberration-correction technology has been developed (23) and successfully applied to visualize local electric fields in ferroelectric materials even at the atomic scale (24) and built-in electric fields at a p-n junction in semiconductor materials (25). This system can also be applied to directly visualize local magnetic fields inside materials at very high resolution (see note S1 and figs. S1 and S2 for a brief introduction). One of the unique features of the system is its simultaneously in-focus and selective visualization of magnetic and structural defects. Taking full advantage of the system, we investigate the influence of structural defects (such as edges, dislocations, and small-angle grain boundaries) on magnetic skyrmions in a thin film of FeGe_1−xSi_x. Here, we report a unique core structure of a magnetic skyrmion domain boundary induced by an “edge” of a crystal grain.

RESULTS AND DISCUSSION

Figure 1A shows a transmission electron microscopy (TEM) bright-field image of a thin-film specimen prepared from a polycrystalline bulk FeGe_1−xSi_x ingot. Only three grains (designated as I, II, and III) are labeled in the field of view. The area bounded by a white rectangle is enlarged in Fig. 1B. Selected-area diffraction analysis (fig. S3 and table S1) and STEM energy-dispersive x-ray (EDX) analysis (fig. S4 and table S2) show that the three grains are crystallographically and compositionally different. Only grain I displays the B20 crystal structure, whereas the other two grains have different crystal structures. Therefore, three interfaces between these grains (as shown in Fig. 1B) are all heterointerfaces between different phases. In particular, the interface between grain I and grain II is better regarded as an edge rather than as a crystalline grain boundary. Thus, magnetic stripes and skyrmions are observed only in grain I, as described in detail in the following sections. Figure 1C is a selected-area electron diffraction pattern obtained from grain I, whereas Fig. 1D is an atomic-resolution high-angle annular dark field (HAADF) STEM image with the specimen tilted by a few degrees so that the [211] zone axis of grain I is aligned parallel to the electron optical axis. Atomic compositions of grain I are evaluated as FeGe_0.75Si_0.25 on STEM EDX analysis. Agreement between the experimental image and the atomic model (Fig. 1E) indicates that the projected c axis lies almost in the horizontal direction of the figures and that the grain boundary between grain I and grain II is nearly parallel to the c axis in the central field of view in Fig. 1B. As the grain boundary gradually changes its orientation upward in the left field of view of Fig. 1B (as indicated by the arrows), two crystal grains (grains I and II) show a number of bend contours suggesting the presence of residual strain. However, the crystallographic orientation and chemical composition of grain I are almost uniform, at least in the area where magnetic stripes and skyrmions are observed in the present study. The thickness of the film was estimated to be around 100 nm in the field of interest in the following figures.

Fig. 1. TEM/STEM characterization of a thin film of FeGe_1−xSi_x.

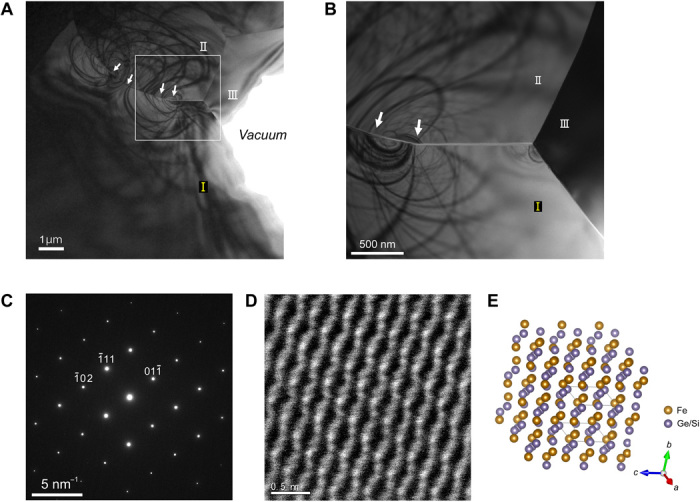
(A) Low-magnification TEM bright-field image of the thin film. Only three grains are labeled as I, II, and III. The arrows indicate the grain boundary between grain I and grain II. (B) Higher-magnification image of the area designated by a white rectangle in (A). (C) Selected-area electron diffraction pattern obtained from grain I. (D) HAADF STEM image obtained from grain I. (E) Atomic model viewed along the [211] zone axis.

When the specimen was cooled down to a nominal temperature of 150 K, magnetic stripes with a period of about 50 nm emerged only in grain I. These values are consistent with the reported Curie temperature and helical pitch of the bulk (13). Figure 2A is a magnetic helicity image (26) that clearly shows magnetic stripe contrast. Here, the magnetic helicity image m is defined by

$$\mathit{m}\equiv -\frac{\partial {\mathrm{\theta }}_{\mathit{x}}}{\partial \mathit{x}}-\frac{\partial {\mathrm{\theta }}_{\mathit{y}}}{\partial \mathit{y}}\propto {\displaystyle \int }(\frac{\partial {\mathit{B}}_{\mathit{y}}}{\partial \mathit{x}}-\frac{\partial {\mathit{B}}_{\mathit{x}}}{\partial \mathit{y}})\mathit{d}\mathit{z}\propto {\displaystyle \int }(\frac{\partial {\mathit{M}}_{\mathit{y}}}{\partial \mathit{x}}-\frac{\partial {\mathit{M}}_{\mathit{x}}}{\partial \mathit{y}})\mathit{d}\mathit{z}=\overline{{(\nabla \times \mathbf{M})}_{\mathit{z}}}\cdot \mathit{t}$$ (1)

where θ_x and θ_y denote the x and y components of the Lorentz deflection angle, B_x and B_y denote the x and y components of the magnetic field, M_x and M_y denote the x and y components of magnetization, and M denotes magnetization. The bar represents the average over film thickness t. The image is related to the magnetic helicity of a skyrmion. A skyrmion with a counterclockwise rotation of magnetization viewed from the electron source (as shown in Figs. 3 and 4) exhibits bright disc contrast, whereas a skyrmion with a clockwise rotation is visualized as dark disc contrast. The stripe contrasts in Fig. 2A originated from the formation of the helical magnetic structure. The inset shows an enlarged view of the stripes in the vicinity of the edge. On careful observation, the stripes appear to change their direction in the vicinity of the edge and to intersect with the edge in an almost perpendicular direction, resulting in the formation of dislocation-like structures, as indicated by the arrows. This suggests that the magnetic stripes are strongly influenced by the presence of the edge. A similar influence of an edge on a magnetic skyrmion in an artificially confined geometry was reported in recent literature (27). On the other hand, magnetic stripes are also affected by the applied magnetic field. This is exemplified as circular stripes in Fig. 2B. Such circular stripes are created by an instantaneous application of a perpendicular magnetic field (>1 T) on the specimen. In addition to the magnetic helicity images, a color vector map of the in-plane magnetization can also be reconstructed as shown in Fig. 2 (C and D). Here, the two different parts near grain boundaries are shown. In these images, it is now clear that the differently oriented magnetic stripes are indeed different magnetic stripe domains.

Fig. 2. Magnetic stripes emerging under zero field–cooled conditions at 95 K.

(A) Magnetic helicity image showing clear stripe contrast in the vicinity of grain boundaries. (Inset) An enlarged image near the triple junction of the three grains indicated by a blue rectangle. Arrows indicate magnetic dislocation–like structures. (B) Circular stripes that emerged after the application of an intense perpendicular magnetic field. (C and D) Reconstructed in-plane magnetization vector maps obtained by DPC STEM in two different areas near the grain boundary between grain I and grain II.

Fig. 3. Skyrmion hexagonal lattice in the vicinity of grain boundaries.

(A) Reconstructed in-plane magnetization vector map of a hexagonal skyrmion lattice. (B) Corresponding magnetic helicity and (C) annular dark field image. (D) Enlarged view of the skyrmion lattice shown in (A).

Fig. 4. Core structure of the skyrmion Σ7 domain boundary.

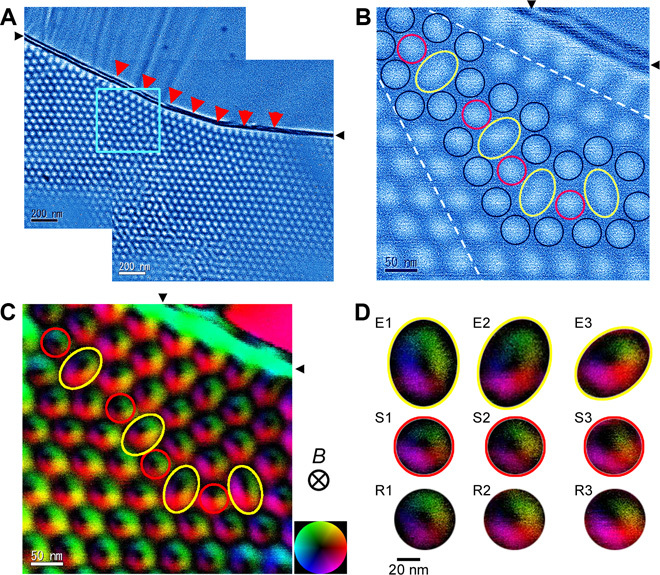
(A) Large field-of-view magnetic helicity image. Two helicity images are merged to show the whole domain boundary structure (see fig. S3 for original images). (B) Enlarged magnetic helicity image of the region indicated by a blue rectangle in (A) showing the core structure of the skyrmion Σ7 domain boundary. (C) DPC reconstructed in-plane magnetization map of the skyrmion domain boundary shown in (B). (D) Extracted images of individual skyrmions in the domain boundary core region. The elongated (E1-E3), shrunk (S1-S3), and regular (R1-R3) images of skyrmions can be found.

Next, when a perpendicular magnetic field (~130 mT) was applied at a nominal temperature of 95 K, a hexagonal skyrmion lattice emerged, as shown in Fig. 3A. Figure 3C shows the simultaneously obtained annular dark field image as a reference. It appears that the skyrmion lattice is oriented with the edge. Figure 3D is a higher-magnification image showing that the direction of magnetization rotation is counterclockwise, as indicated by a circular arrow. This sense of magnetization rotation is clearly visualized as bright disc contrast in the magnetic helicity image shown in Fig. 3B. Here, we often find fluctuations in the size and shape of individual skyrmions within the lattice. For example, in Fig. 3D, the middle rows of the skyrmion appear larger and elongated in the vertical direction compared with the other rows, as indicated by two scale arrows with the letters S (small) and L (large). Such a change in the size and shape of the skyrmion is not an artifact caused by the scanning of the electron beam. It appears that the size and shape of individual skyrmions are not severely fixed but can be changeable within the skyrmion lattice.

In the vicinity of grain boundaries between the two grains (grains I and II), we found the formation of the skyrmion domain boundary as shown in Fig. 4A. This image is created by connecting two magnetic helicity images to obtain a larger field of view of the skyrmion domain boundary structure (the connecting process is shown in fig. S5). The magnified view of the skyrmion domain boundary is shown in Fig. 4B. The orientation relationship between two adjacent skyrmion domains is determined to be Σ7, according to the CSL theory for grain boundaries (28). In crystalline grain boundaries, the Σ7 orientation is known to be one of the most stable grain boundaries in hexagonal crystal systems (29). It is surprising that such a stable orientation domain boundary can also be formed in the skyrmion lattice. As already mentioned, the orientation of a magnetic helical structure before skyrmion formation is strongly influenced by edges. Owing to the trace of such a strong interaction, the skyrmion lattice appears to follow the orientation changes in the vicinity of the edge, as indicated by a series of red arrowheads. As a result, skyrmion “Σ7” domain boundary is formed near the edge.

As indicated by black, red, and yellow circles in Fig. 4B, the domain boundary structure can be described by the periodic combination of fivefold coordinated and sevenfold coordinated structure units, as frequently observed in Σ7 grain boundaries in real atomic crystals (29). However, there is a distinct difference. Our direct imaging of the core structure clearly shows that the size and shape of a skyrmion can be flexibly changed at the domain boundary core regions, as indicated by the red and yellow circles in Fig. 4 (B and C). The yellow circle is apparently elongated (elliptical), whereas the red circle appears slightly smaller. Figure 4D shows the extracted images of individual skyrmions in the domain boundary core region, exhibiting elongated (E), shrunk (S), and regular (R) shapes and sizes. From a preliminary quantitative analysis (fig. S6), the distortion is as large as 60% for the apparent elongation. Such a change in the size and shape of individual skyrmions at the domain boundary core is not specific to this area. Figure S7 shows another example of Σ7 domain boundaries found in a thicker region of the film. This image also shows that the individual skyrmions at the Σ7 domain boundary core change their size and shape in a similar manner.

For the structure relaxation of grain boundaries, the role of intrinsic free volume changes in their cores should be considered. In atomic crystals, atomic rearrangement or foreign atom segregation is a common feature that accommodates excess free volumes of grain boundary cores and thus reduces the grain boundary total energy. In skyrmion domain boundaries, on the other hand, deformation of the size and shape of individual skyrmions can be an additional relaxation mechanism to stabilize their core structures. This should originate from the flexible nature of magnetic skyrmions. For a thorough understanding of our experimental findings, future theoretical investigations with the aid of micromagnetic simulations are needed.

In conclusion, we used DPC STEM to directly observe the core structure of the skyrmion Σ7 domain boundary in a thin film of FeGe_1−xSi_x (x ~ 0.25). We found that individual skyrmions at the domain boundary cores can flexibly change their size and shape to stabilize their core structure. This structural relaxation mode is a peculiar characteristic of the skyrmion domain boundary. Such flexibility in size and shape should be a fundamental characteristic of individual magnetic skyrmions and may be utilized in future device applications.

MATERIALS AND METHODS

Polycrystalline FeGe_1−xSi_x was grown from an FeGe_0.8Si_0.2 ingot annealed at 900°C for 100 hours by conventional solid-state reaction. A thin-film specimen was fabricated from a bulk crystal using an ion slicer (EM-09100IS; JEOL Ltd.). Before the observation, the thin film was further polished with a low-voltage and low-angle Ar ion beam milling apparatus (Precision Ion Polishing System II; Gatan Inc.) and an ion cleaner. The thin-film specimen was first characterized using a conventional TEM (JEM-2010HC; JEOL Ltd.). Atomic-resolution HAADF STEM images were obtained using an aberration-corrected scanning transmission electron microscope (JEM-ARM200F; JEOL Ltd.). For DPC STEM observations, we used a scanning transmission electron microscope (JEM-2100F; JEOL Ltd.) equipped with a probe-forming aberration corrector (CEOS GmbH) and a Schottky field emission gun operated at 200 kV. This microscope was equipped with a SAAF detector, which is described in detail in the literature. To observe the helical and skyrmion magnetic order emerging at low temperatures, we used a double-tilt liquid-nitrogen cooling specimen holder (model 636; Gatan Inc.). Analysis of DPC STEM images was performed either online using a direct reconstruction system or offline using a program written by T.M. in Digital Micrograph Scripting language (Gatan Inc.).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/2/e1501280/DC1

Note S1. Brief description of the DPC STEM system.

Fig. S1. Schematic of DPC STEM.

Fig. S2. Reconstruction processes in DPC STEM.

Fig. S3. Selected-area electron diffraction patterns from 10 numbered areas.

Fig. S4. HAADF STEM image of the area near the structural grain boundary between grain I and grain II, where we performed STEM EDX characterization.

Fig. S5. Process to synthesize Fig. 4A.

Fig. S6. Preliminary quantitative analysis of the flexibility of skyrmions.

Fig. S7. Another example of magnetic Σ7 domain boundary.

Table S1. Specimen tilting angles for the selected-area electron diffraction patterns listed in fig. S3.

Table S2. STEM EDX characterization of the thin film.