Table 1. Voltage stability condition applied to 11 test networks.
| Numerical testing of theoretical predictions | ||||
|---|---|---|---|---|
| Test case (1,000 instances) | Condition correctness | Exact deviation (δexact) | Predicted deviation (δ−) | Condition accuracy |
| 9 bus system | True | 5.50·10−2 | 5.52·10−2 | 3.56·10−3 |
| 14 bus system | True | 2.50·10−2 | 2.51·10−2 | 1.96·10−3 |
| RTS 24 | True | 3.28·10−2 | 3.29·10−2 | 3.28·10−3 |
| 30 bus system | True | 4.72·10−2 | 4.75·10−2 | 7.64·10−3 |
| New England 39 | True | 5.95·10−2 | 5.99·10−2 | 5.97·10−3 |
| RTS ‘96 (2 area) | True | 3.44·10−2 | 3.45·10−2 | 3.81·10−3 |
| 57 bus system | True | 0.97·10−1 | 0.99·10−1 | 2.97·10−2 |
| RTS ‘96 (3 area) | True | 3.57·10−2 | 3.58·10−2 | 3.94·10−3 |
| 118 bus system | True | 2.68·10−2 | 2.69·10−2 | 3.63·10−3 |
| 300 bus system | True | 1.32·10−1 | 1.36·10−1 | 3.03·10−2 |
| Polish 2,383 system | True | 4.03·10−2 | 4.06·10−2 | 8.55·10−3 |
Condition correctness is whether the implication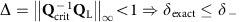 
holds for every network realization, where 
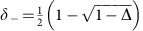and δexact is determined numerically. Exact and predicted deviations are averaged values of the respective quantities over all realizations. Condition accuracy is calculated as (δ−−δexact)/δexact, and averaged over 1,000 randomized instances for each network, with 30% of generation (resp. 30% of load) randomized by 30% (resp. 50%) using a normal distribution centred around base conditions.