Multiscale musculoskeletal modelling, data–model fusion and electromyography-informed modelling

Abstract

This paper proposes methods and technologies that advance the state of the art for modelling the musculoskeletal system across the spatial and temporal scales; and storing these using efficient ontologies and tools. We present population-based modelling as an efficient method to rapidly generate individual morphology from only a few measurements and to learn from the ever-increasing supply of imaging data available. We present multiscale methods for continuum muscle and bone models; and efficient mechanostatistical methods, both continuum and particle-based, to bridge the scales. Finally, we examine both the importance that muscles play in bone remodelling stimuli and the latest muscle force prediction methods that use electromyography-assisted modelling techniques to compute musculoskeletal forces that best reflect the underlying neuromuscular activity. Our proposal is that, in order to have a clinically relevant virtual physiological human, (i) bone and muscle mechanics must be considered together; (ii) models should be trained on population data to permit rapid generation and use underlying principal modes that describe both muscle patterns and morphology; and (iii) these tools need to be available in an open-source repository so that the scientific community may use, personalize and contribute to the database of models.

1. Introduction

This paper presents a perspective on state-of-the-art methods and technologies that are needed to establish a clinically relevant virtual physiological human (VPH). We propose suitable methods in geometry development, numerical methods, storage and sharing of musculoskeletal models in order to collectively advance the field of musculoskeletal modelling as a scientific community.

Musculoskeletal methods can be made more patient-specific in geometric shape, material behaviour and relevant bio-signals (through the use of muscle electromyography (EMG)). Personalized geometry is possible using ‘free-form’ deformation [1] or segmentation from computed tomography (CT) and/or magnetic resonance imaging (MRI) but would not be clinically feasible due to the need for rapid model generation. Specifically, MRI is not easily segmented using automated methods, ‘free-form’ deformation requires careful selection of anatomical landmarks and additional smoothing constraints to obtain a realistic anatomical profile, and CT is less desirable due to ionizing radiation. General uniform scaling methods [2,3], such as those used in OpenSim, are not accurate enough to capture anatomically realistic geometric shape variations and are not suitable for pathological populations. Recent geometric construction methods have been converging towards population-based approaches, using statistical methods that capture the natural variations in the form and function of the musculoskeletal system. They may be used to intelligently segment an individual [4], or predict individual geometry using multivariate statistical methods [5]. Statistical modelling also allows quantitative comparisons between populations, identification of trends across populations and diagnostic and prognostic predictions.

Musculoskeletal tools must incorporate both multiscale and multi-physics in order to address clinical problems that manifest at different hierarchical levels, such as at the whole organ, meso-, micro- and cellular levels. In order to address these challenges, we need to adopt suitable numerical methods that are appropriate to different scales and incorporate statistical methods to capture mechanics at finer scales that may be homogenized and integrated with whole organ-level mechanics efficiently. We also need to adopt modelling frameworks and define modelling ontologies and tools that describe information at each scale. To date we see the Physiome Project [6] and its numerical and graphical engines (OpenCMISS and CMGUI) [7] and the associated markup languages (CellML and FieldML) [7–10] as one effective suite of tools for sharing and communicating models to the scientific community. The Musculoskeletal Atlas Project [11] (MAP) is a recent development that links previously collected models and imaging data with population-based statistical tools and widely used modelling platforms, including Abaqus, FEBio and OpenSim.

Modelling methods must be integrative and holistic, including muscle, bone, cartilage and neural modelling, rather than being applied in isolation. The mechanical structure of bone and its remodelling response are heavily influenced by its loading conditions, which are a result of our daily interactions with the environment. Movement, for example, results from an orchestrated and selective activation of muscles generating force to induce joint torques in order to consciously navigate through the environment. The force generation is achieved through complex processes on multiple scales and multiple parts of the musculoskeletal system; for example, the generation of neural stimuli in the spinal cord, transmission of signals from the nerve to a muscle's neuromuscular junctions, force generation within skeletal muscle sarcomeres, force transmission to the tendons and sensory feedback to the nervous system. These processes are extremely complex, strongly coupled with each other and by far not fully understood. A better understanding of the structure and function of the neuromuscular system would allow us an improved understanding of neuromuscular disorders and therefore lead to improved diagnosis and treatment. In addition, an improved understanding would provide us with valuable input for prevention measures when planning ergonomic environments.

Finally, the use of electrophysiological inputs into muscle models has been incorporated through EMG signals, a surrogate for underlying muscle activation. The mechanisms underlying joint function and body movement are a reflection of the interacting dynamics of the composite neuromusculoskeletal system. Therefore, even if one aims to characterize the local mechanical environment of specific skeletal tissues, the broader neuromusculoskeletal mechanisms underlying the observed tissue loading need to be accounted for. Joint function is the ultimate result of muscle forces modulated by neural commands generated by populations of spinal motor neurons and sensory afferents. In this context, despite the detailed knowledge that we have about function of neural or mechanical structures in the human body, we currently have little relevant information to establish cause–effect relationships across them in vivo in the moving human. This currently represents the major open challenge to the understanding of human movement. In this paper, we discuss the latest developments in EMG-based models that to date have provided some of the best matches to the instrumented in vivo knee joint force as part of the ‘grand knee challenge’ [12,13].

1.1. Population models and the Musculoskeletal Atlas Project

Focusing on the femur, we review recent works that have demonstrated statistical methods to showcase the power and need for population modelling in the field of musculoskeletal biomechanics. This is intimately linked with the MAP, an open-source model-generation software and a cloud-based data, model and workflow database that addresses the challenges of the VPH.

Population-derived models typically involve the collection of a ‘training set’ of parametrized and normalized data. In the case of geometric modelling, this involves collecting typically segmented geometries and identifying correspondent landmarks (such as consistent bony protrusions) located on all segmentations, then using a Procrustes transform to align landmark sets [4]. A statistical analysis such as principal component analysis can then be performed on the data to reduce its dimensionality and reveal significant modes of variation or correlation. Population models of the femur, as with many other structures, usually begin by building statistical models of its shape and appearance [14,15]. The most immediate applications for shape models are image segmentation [16,17] and shape reconstruction [18]. Automated image segmentation allows large populations of data to be collected while shape reconstruction from landmarks and partial surfaces efficiently produces geometries for surgery planning, muscle paths via insertions, patient classification [19] and patient-specific modelling.

Beyond shape, population models can include internal femur architecture [17,20], correlations to fracture and disease risk [14,21], mechanical behaviour [22] and anthropological and anthropometric data [5]. These models allow the prediction of femoral structure from correlated data, or vice versa. In the case of statistical models relating structure to mechanical behaviour, the ability to predict internal stresses and strains via a statistical model offers a computationally efficient means to compute stresses, such that real-time clinical applications become possible [23].

Population modelling has also been used in conjunction with discriminant analysis to identify biomechanical features of dynamic gait waveforms associated with ageing [24] and pathology [25,26]. Although useful for the classification of normal or pathological gait, the weights obtained from a principal component analysis can also be used to synthetically generate feasible gait data across a larger population than what was originally sampled [27]. This can be useful for assessing the variability in biomechanical parameters across a population and has application to predict femur fracture risk [22] or assess joint replacement designs [27]. Population models might also be used to predict complex form–function relationships of the musculoskeletal system. For example, knowledge of knee geometry can be used to predict the knee joint alignment [28], joint kinematics and joint mechanics [29].

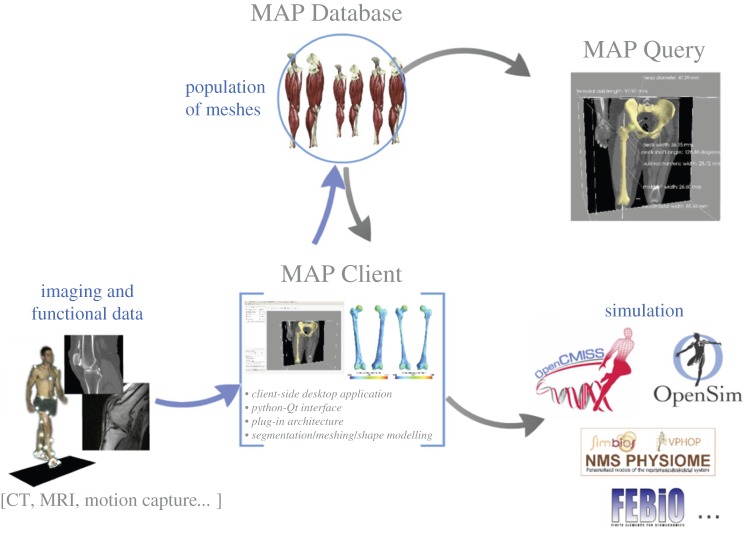
Population modelling has many applications for understanding the form and function of the musculoskeletal system. The methods and applications presented thus far are invariably workflows that combine many steps to create and use statistical models for a specific purpose. Steps such as segmentation, landmarking, registration and model reconstruction are common across many workflows and are essential tools for population modelling. Also essential to population modelling are the population data themselves. To facilitate the use of population modelling for musculoskeletal applications, we have created the MAP (figure 1), an open-source software framework, to: (i) consolidate the essential tools of musculoskeletal population modelling with an easy-to-use interface—the MAP Client, and (ii) provide a repository for imaging, functional and model data across a population—the MAP Database.

Figure 1.

Schematic of the MAP, composed of the MAP Database, the MAP Client and the MAP Query tool. The goal of the MAP is to streamline the generation, storage and use of musculoskeletal models. (Online version in colour.)

1.2. The Musculoskeletal Atlas Project Client

The MAP Client is a Python-based open-source workflow manager for musculoskeletal model generation. The tools to generate a model, such as segmentation and registration, are implemented as plugins, or steps, which can be linked together in a graphical user interface (GUI) to produce a workflow (figure 2).

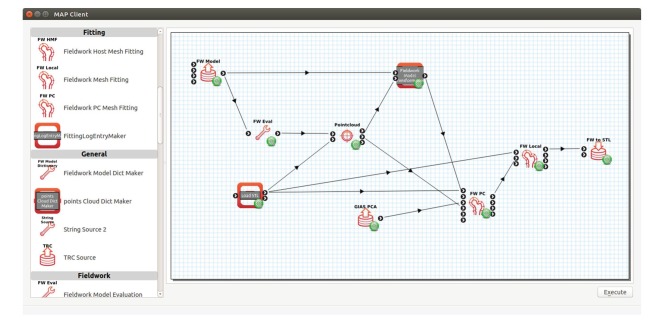
Figure 2.

The MAP Client user interface. Installed plugins are shown on the left and an assembled workflow for reconstructing femur shape from proximal femur geometry is shown in the workspace on the right. (Online version in colour.)

The MAP Client is designed around ease of use and community engagement. The GUI allows novice users to execute workflows containing complex steps, while steps can be quickly written in the Python language with the aid of the in-built plugin wizard. The plugin framework is lightweight, requires no external libraries and is compliant with both Python 2 and Python 3, facilitating cross-platform use. Framework documentation and tutorials can be found in https://map-client.readthedocs.org/en/latest/index.html. Currently, a workflow has been developed for the generation of lower limb bone models from motion capture and imaging data [15]. Key steps include segmentation, landmark viewing and annotation, point-cloud registration, shape model-based non-rigid registration and surface mesh fitting. The purpose of this workflow is to rapidly generate accurate bone models that are compatible with OpenSim, an open-source musculoskeletal modelling package [2].

Another example of a MAP Client workflow is one for reconstructing whole femur geometry from proximal femur segmentation (figure 2). In this example, the geometry of the whole femur is needed to apply realistic muscle forces to simulate stresses in the hip; however, medical imaging data are only available for the proximal femur. A femur shape model is first used to reconstruct a realistic femur based on surface data segmented from hip MRI. An STL Source Step and a Model Source Step import the segmentation and the mean femur model, respectively. The proximal portion of the femur model is then discretized into a data cloud by a Model Evaluation Step. The data cloud and segmentation are input to the Pointcloud Rigid-body Registration Step in which the data cloud is registered to the segmentation using an iterative closest point approach [30]. The registration transformation is output to a Model Transformation Step, which applies the transformation to the mean femur model to bring it into alignment with the segmentation. A Principal Component Mesh Fitting Step takes the transformed model, the segmentation and a set of principal components (imported by a PC Source Step) to non-rigidly fit the model to the segmentation along its principal components. The fitted model is output to a Model Local Fit Step, which performs a final fine-scale fit of the model to the segmentation to improve accuracy in the proximal femur. Finally, the fitted model is passed to an Export STL Surface Step, which writes the model as an STL file. The final model can then be used for computational modelling, such as rigid body dynamics or finite-element analysis. Workflows implemented in the MAP Client abstract the implementation details so that users focus on the process at hand. Importantly, workflows and steps can be saved and shared with others so that methodologies implemented as MAP Client workflows can be readily validated and implemented by others.

1.3. The Musculoskeletal Atlas Project Database

The MAP Client is complemented by the MAP Database, which stores workflows and associated steps. The MAP Database also functions as a repository for models, workflows, steps and associated imaging and functional data. The MAP Database is built upon the Physiome Model Repository [31], which includes access control, annotation and search tools, and a distributed version control system. One rationale for developing the MAP Database is to facilitate exchange of models and data to accelerate the field of computational biomechanics. Researchers around the world are creating models and generating simulations that, for the most part, are never shared or used outside the original intent of the investigators' primary goal. The potential for computational models to have clinical impact and build upon prior knowledge is limited by our inability to share, test and openly validate each other's models. The MAP Database will address this limitation with the goal of providing access to thousands of datasets and associated models. Coupled with population modelling methods, this repository promises to bring us closer to clinical adoption of computational models.

2. Multiscale continuum mechanics of bone

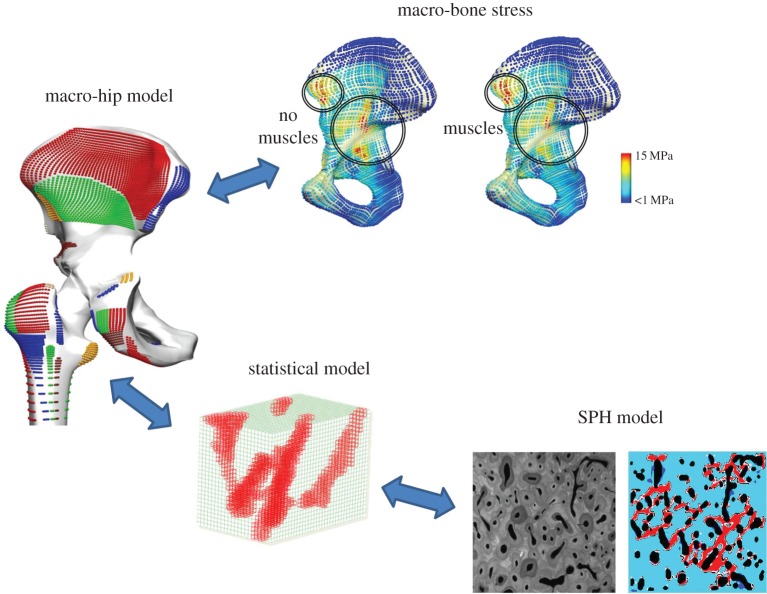
Whole joint models may be derived from population-based approaches detailed in §1; however, the hierarchical structure of bone presents a challenge to model efficiently and capture important spatial behaviour to understand the mechanisms of ageing, disease and fracture. At the continuum level, bone can be assumed to have an anisotropic behaviour with a constitutive description informed from underlying microstructures. These underlying structures are influenced by bone strain, which in turn is informed by muscle forces [32] such as the anatomical muscle loading considered in §§3 and 4. Computational microstructural bone adaptation has been well represented in the literature for trabecular bone [33,34] and evaluated against in vivo loaded murine bone [35]. A more recent approach has been based on particle-based schemes; and efficient methods of linking underlying remodelling mechanics to the whole bone using statistical methods similar to those presented in §1. Figure 3 describes the proposed multiscale bone mechanics framework, where a smooth particle hydrodynamics (SPH) model captures microstructure-level bone remodelling, which has a two-way communication via statistical methods to the whole hip. EMG-based muscle forces from walking stimuli are used to drive remodelling at the whole hip joint, which is solved using finite-element modelling. The SPH microstructure bone model predicts porosity and homogenized Young's modulus given a load from the whole hip finite-element model. The SPH model is repeatedly run on a population of loading scenarios and a multivariate statistical model, such as partial least-squares regression (PLSR), is then trained to relate Young's modulus to a given load. The PLSR statistical model can then be rapidly called upon to predict remodelled bone strength given whole hip loads. In this framework, finite-element methods are more suited to whole-body continuum static simulations, but are linked via statistical methods to particle-based schemes, which are computationally expensive but capture dynamic behaviour at finer scales better.

Figure 3.

Multiscale bone modelling framework consisting of a two-way information flow between muscle forces, bone mechanics, statistical model and micro-level SPH particle mechanics. An SPH model simulates microstructure bone remodelling, which is captured in a statistical model and rapidly called from a whole hip model. EMG muscle forces from walking stimuli drive the bone remodelling. (Online version in colour.)

Particle-based methods allow us to understand very fine micro-mechanical behaviour associated with bone remodelling and micro-fracture. SPH is a continuum method but belongs to the family of meshless particle-based numerical methods. The key benefit is that it easily captures highly filamentary fracture patterns and evolving Haversian canals (or ‘cutting cones') in cortical bone. Modelling bone cracks and evolving structures due to remodelling is challenging using traditional finite-element modelling due to the need for the mesh to match the geometry of the discontinuity and the mesh must be regenerated at each step [36]. A recent implementation of SPH [37] evaluated the influence of loading stimulus and age on the growth of Haversian canals. The study also presented a unique hypothesis that large cortical bone pores in older age are a result of the coalescence of smaller Haversian canals that merge due to stress shielding in bone. The SPH method was able to capture patterns of remodelling that have been clearly observed in synchrotron imaging. The model also demonstrated sensitivity to subject-specific pore distribution, initial bone density, loading patterns and osteocyte density. All these features are key variables that need to be considered at the bone micro-scale, and SPH is a suitable numerical method to model with this level of fidelity.

A challenge of modelling at finer scales is how to link results with meso- and macro-level structures efficiently. Homogenizing microstructures that lead directly to macroscopic stress tensors can be computed analytically or numerically; however, typically we simulate different microstructural scenarios under different loading conditions, which can lead to a whole population of models. This has motivated the application of statistical approaches such as PLSR to link spatial scales by developing pre-computed surrogate models, such as the mechanostatistical model of cortical bone remodelling reported by Wang et al. [38]. Population models were used to train femur shape prediction in §1 and here we train a statistical model on synthetic finite-element mechanics. A unique aspect of Wang's study was that the model was derived using equine data (due to similar structures to humans) with in vivo strain gauge data for different speeds of gait to inform the ‘mechanostat’ [39] used to decide states of bone remodelling, and bio-staining data to quantify rates of bone remodelling. The model simulated the ‘cutting-cone’ phenomenon, which was directed towards damaged bone or regions of low strain stimulus according to Wolff's law. A ‘fading memory’ model was also used to capture the effect that bone remembers its recent history of loading even if one stops exercising. These complex features were then simulated for different loading states and Haversian canal configurations to train the PLSR surrogate model. All these mechanical effects were then linked to the femoral neck (a known region that fails) by calls to the statistical model. A mechanics model that would normally run in hours was solved in seconds, making this approach highly translatable to the clinic. The statistical model is evaluated by predicting mechanics solutions that are not part of the original training set.

The local variations in bone density and trabecular bone strut alignment are due to the daily loading stimulus that bone senses [40]. In fact, almost half the load at a joint is attributed to muscle forces crossing it; hence, confidence in evaluating bone remodelling requires confidence in muscle force prediction. To illustrate this idea, muscle forces developed using the EMG-assisted method (§4) were used to inform bone remodelling patterns in the acetabulum of the hip [41]. A detailed finite-element model of the hip joint was developed from a Somso model (www.somso.de) including muscle origins and insertions, material properties from CT Hounsfield units and validated against a Sawbone model (www.sawbones.com) using an Instron compression test. The model was firstly simulated using the total net force loaded through the joint centre, and secondly using the equivalent load distributed between the ground reaction force and supporting muscle forces. Firstly, it was observed that muscles distribute the loads more evenly across the pelvis and reduce the peak von Mises stresses by up to 30%, as shown in figure 3 (top) and also confirmed by the work of Dalstra et al. [42]. Hence, regions of bone remodelling stimuli can be overestimated when anatomically accurate muscle forces are not considered. Secondly, regions of remodelling around the acetabulum, which showed increased stress due to muscle insertions, corresponded with high density observed using CT phantom values. This shows that incorporating muscles partly explains the spatial variation of bone density. Having confidence in muscle loading patterns is important for bone remodelling predictions and §§3 and 4 present new developments in EMG-assisted muscle force prediction.

3. Multiscale continuum mechanics of muscle

Within a clinical setting, one of the few directly and easily accessible functional data of the neuromuscular system are EMG recordings. EMG signals can be recorded using surface or needle electrodes. Needle EMG electrodes are invasive and typically only pick up signals from a few motor units near the electrode. By contrast, surface EMG electrodes are non-invasive but only detect the activity of muscles underneath the electrode, i.e. near the surface. The activity of deeper muscles cannot be directly measured using surface EMG and, hence, needs to be estimated using neural-based EMG-assisted methods (§4). Furthermore, the complex functional grouping of muscle fibres into motor units, their distribution within the muscle volume, and their complex structural embedding within the extracellular matrix provide geometrical and mechanical uncertainty leading to drawbacks in analysing EMG signals and, hence, currently limit us to using EMG signals to derive robust clinical EMG-based markers for specific diseases.

Advancements in electrode design and signal processing nowadays provides promising and new ways of decomposing experimental high-density surface EMG signals into individual motor unit discharges [43]. Despite the potential of these methods, high-density EMG has yet to gain widespread clinical acceptance. While these electrodes have already successfully been used to investigate muscular function under isometric conditions, there is still some uncertainty for interpreting non-isometric contractions since the muscle as the source of the electrical signals (action potentials), which are picked up by the electrode, moves relative to the electrode on the surface of the skin. If anatomical structures are taken into consideration, simulations could provide further insights for improving source localization. However, state-of-the-art computational models of the EMG focus on the signal processing part and often neglect or simplify the anatomical arrangements of the muscle fibres. Despite all advancements, the link between the neural control and the response of a particular muscle is not always clear.

Considering the non-isometric case of analysing EMG data, one would obtain a much improved understanding of the neuromuscular system and its disorders by employing simulations. To do so, detailed biophysical models that are capable of describing the complex mechanisms from the neural drive to the generation of muscle force [44] leading to the resulting EMG signals [45] need to be developed. However, existing chemo-electro-mechanically based models need to be extended in order to consider micro-mechanical descriptions of the skeletal muscle tissue similar to those describing the interplay between the force-generating fibres and the extracellular matrix (e.g. [46]).

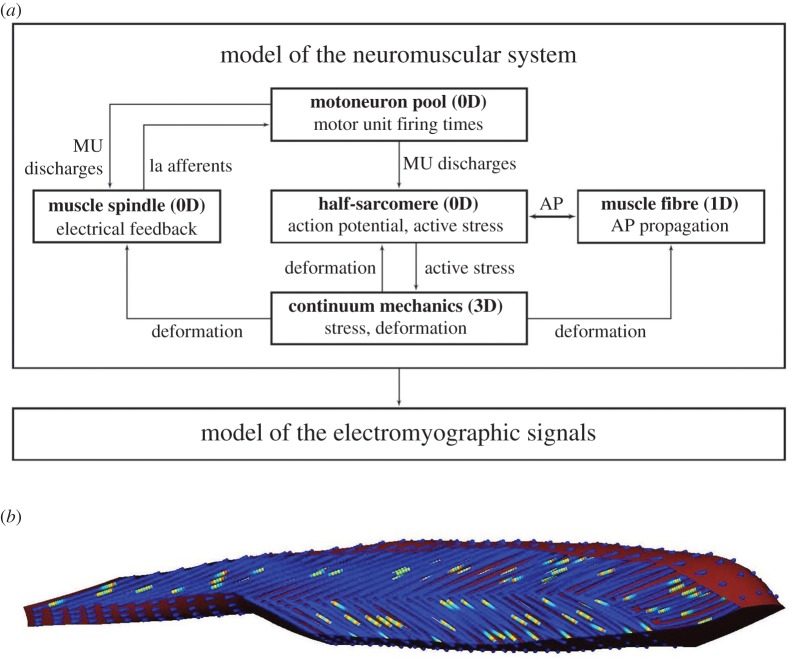
From the chemo-electro-mechanical point of view, multiscale biophysical models exist that describe the entire pathway from electrical excitation to muscle force generation [47–49]. In these models, a biophysical cellular model predicts the stresses that result from the activation-induced contraction of the half-sarcomeres. These sarcomere-based active stresses are homogenized before being included in a continuum-mechanical constitutive equation describing the relationship between tissue deformation (strain) and stress distribution. By solving the discretized governing equations of the continuum-mechanical model, one obtains the deformed geometry of the muscle as well as the resulting muscle forces. Since each contraction within a muscle fibre is induced through an action potential that propagates along the respective fibre, the electrical state of the muscle tissue is known, and, therefore, the resulting (surface) EMG signal can be computed using the bidomain equations [45]. A short overview of the interconnected model components, which have been implemented within the open-source software library OpenCMISS [7], is given in figure 4.

Figure 4.

(a) Overview of the components included within the biophysical model of the neuromuscular system capable of predicting the EMG signal for complex geometries and during deformation of the skeletal muscle. AP, action potential; MU, motor unit; 0D, 1D, 3D, reference to the dimensionality of the underlying governing equations. (b) Geometry of the tibialis anterior muscle with fibre distribution indicating the local potential. (Online version in colour.)

Besides the aforementioned framework, the only other existing true multiscale framework for modelling the chemo-electro-mechanical behaviour of skeletal muscle tissue has been recently proposed by Ivanović et al. [50]. Within this work, the authors focus on high-performance computational aspects of their chemo-electro-mechanical model and ignore the possibility of incorporating biophysical-based recruitment models. Two other existing multiscale skeletal muscle models [51,52] can be categorized as electro-mechanical skeletal muscle models, in which the authors do not solve for the underlying biophysical processes on the cellular level but rather assume a phenomenological behaviour of the electrical signal.

The biophysical description has many advantages over simpler, phenomenological models. Physiological effects, such as membrane fatigue causing changes in the amplitude or action potential propagation velocities, are derived based on the model rather than being prescribed as part of the model construction. Despite the fact that many material parameters of such a comprehensive model cannot be determined on a patient-specific basis, the model provides a step forward to determine and identify mechanisms present in muscular function and dysfunction.

While models of the EMG led to an improved understanding of the electrophysiological behaviour of skeletal muscles, they are not necessarily suitable for analysing the mechanical state of the underlying muscles. Hence, the EMG and the chemo-electro-mechanical models need to be further extended by additional measures, mechanisms and data in order to quantify the mechanical behaviour of the skeletal muscle tissue. One possibility is to record, in addition to EMG, mechanical quantities such as muscle vibrations or muscle deformations. One preferred possibility could be magnetic resonance elastography. To correlate specific activation principles with mechanical response, controlled muscle contractions are desired. Since skeletal muscles contract voluntarily, a controlled environment can be achieved by inducing a muscular contraction through functional electrical stimulation (FES). In FES, an external electrical signal is applied to stimulate muscle tissue. To determine the number of muscle fibres that are stimulated through a particular (monophasic or biphasic) impulse, one can also use the above-described modelling framework. In Kim et al. [53], a chemo-electro-mechanical model was used to investigate different electrode arrangements and explore neural spike trains, resulting from the firing rate of the motor neurons on the amount of activated muscle tissue and its effect on fatigue.

4. EMG-based muscle models and validation

At the whole joint scale, gait analysis in conjunction with musculoskeletal modelling has provided opportunities for estimating muscle forces. However, currently available methods largely rely on optimization as a way to solve for neuromuscular redundancy. Because there are more muscles than skeletal degrees of freedom (DOFs), there are multiple neuromuscular patterns that can result in the same joint-DOF state, i.e. DOF moment and acceleration. Optimization is used to select the one neuromuscular pattern that satisfies an a priori defined optimization criterion [54], such as minimizing metabolic cost or total muscle activation. This approach generates systematic and repeatable muscle force patterns for a given joint-DOF state. Therefore, it does not characterize how neuromuscular patterns vary across conditions, i.e. time, motor tasks, training and pathology, even for the same joint-DOF state and within the same person.

An alternative is that of combining current optimization-based modelling methods with muscle electrophysiological recording and processing techniques. Here we provide an overview of the EMG signal processing techniques that we use to extract features of neuromuscular recruitment as well as the modelling formulations that have been recently proposed under this paradigm.

4.1. Extracting neuromuscular features from electrophysiological recordings

Surface EMG recordings can be easily recorded in vivo during dynamic motor tasks. Although limited in terms of selectivity and noise contamination, they encode meaningful information on the muscle neural excitation level. Muscle EMGs are typically high-pass filtered, fill-wave rectified, low-pass filtered and amplitude normalized to extract smooth linear envelopes, i.e. muscle excitations. These give an indication of the time segments a specific muscle is active. In our previous work, we further processed EMG excitations to extract a number of features including muscle-specific activation and low-dimensional synergistic structures of muscle activation [55,56]. The first feature represents normalized levels of muscle recruitment, with ‘zero’ referring to no recruitment and ‘one’ referring to full muscle recruitment, i.e. all muscle motor units recruited and firing at maximal rate. Because motor units fire at non-uniform rates and the resulting action potentials superimpose on each other, the amplitude of the surface EMG picked up by the electrodes is not proportional to the muscle activation and therefore to muscle force and was accounted for by employing a second-order twitch model and a nonlinear transfer function [55]. The second feature can be extracted by processing muscle-specific activation using unsupervised machine learning and dimensionality reduction techniques such as non-negative matrix factorization [56]. This decomposes multi-muscle activations into a lower-dimensional set of non-negative activation primitives and muscle weightings. Linear mixing of primitives and weightings reconstructs most of the variability of the original muscle-specific activations. This suggests that complex muscle activation patterns can be constructed by a small number of synergistic primitives acting on multiple muscles simultaneously.

4.2. Open-loop and closed-loop formulations of EMG-informed musculoskeletal modelling

Neuromuscular features have been successfully extracted from experimentally recorded EMG data as a direct input drive to numerical musculoskeletal models of human limbs, thus accounting for realistic subject-specific neuromuscular strategies [56,57]. In this, muscle and joint dynamics are predicted blindly as part of an open-loop formulation, i.e. with no mechanism that accounts for prediction errors. This model formulation comprises four major components. The activation-mapping component distributes muscle-specific activations or low-dimensional primitives of activations to individual musculotendon units (MTUs) in the musculoskeletal model. The MTU kinematics component synthesizes subject-specific musculoskeletal kinematics models into a set of multidimensional cubic B-splines [58]. Synthesis into continuous functions is crucial for generating differentiable musculotendon kinematics equations and enabling the computation of analytical Jacobians for the forward simulation of the musculoskeletal system. The component receives experimental joint angles as an input and computes MTU kinematics, i.e. length and moment arms. The MTU dynamic component employs a Hill-type muscle model in series with nonlinear elastic tendons to estimate MTU forces from MTU lengths and activations estimated in the previous blocks. The joint dynamic component projects MTU forces to multiple joint-DOFs simultaneously by using MTU moment arms from the previous block. This allows the MTU force to be translated into the joint moment and joint contact force simultaneously [59]. The open-loop model is calibrated to obtain the best predictions of the experimental joint data when only driven by activation patterns and joint angles from a set of calibration trials. It employs a nonlinear least-squares optimization procedure to identify parameters that vary nonlinearly across subjects including: EMG-to-activation parameters, MTU optimal fibre length, tendon slack length and maximal isometric force.

The open-loop formulation is then generalized into a closed-loop modelling formulation [60]. This accounts for surface EMG uncertainties that may contribute to bias the model-based joint dynamics estimates including cross-talk and filtering artefacts as well as the inability to access deeply located muscles. In this, the open-loop EMG-driven modelling formulation is coupled with a static optimization procedure. This enables the input EMG excitations to be adjusted and predicts neural commands for muscles with no EMG data available so that the forward-driven musculoskeletal model tracks experimental joint data about multiple DOFs simultaneously. This provides the flexibility of transitioning from the configuration where muscles are fully driven by experimental EMG signals to the configuration where muscle activation patterns are fully synthesized using numerical optimization. Importantly, we provided a procedure that allows the minimal level of EMG adjustment to be established that results in dynamically consistent simulations.

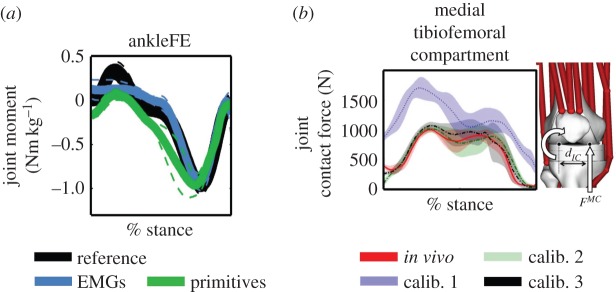
In Sartori et al. [57], we have shown for the first time the possibility of predicting dynamically consistent estimates of joint moments about multiple DOFs simultaneously as a direct function of EMG data as part of an open-loop formulation (figure 5a). In Sartori et al. [56], we showed, for the first time, that it is possible to reconstruct the subject-specific lower extremity musculoskeletal function from a five-dimensional set of muscle synergies with the same accuracy as when using 16 muscle EMG recordings (figure 5a). Results also showed how biomechanically different motor tasks shared similar elementary neural control patterns that project into specialized musculoskeletal functions. Figure 5b shows how open-loop multi-DOF modelling could be employed to blindly generate knee joint contact force estimates that reflected in vivo measurements from instrumented total joint replacements. Finally, figure 6 shows representative EMG excitations minimally adjusted as part of our proposed closed-loop formulation and the resulting improvement in multi-joint moment matching during walking.

Figure 5.

Reference and predicted ankle plantar-dorsiflexion moments (ankleFE) during over-ground locomotion. Joint moments are predicted using open-loop formulations driven by experimental EMG excitations or primitives of EMG excitations. (b) In vivo medial tibiofemoral contact forces and those predicted using an EMG-driven open-loop formulation with three different calibration procedures (i.e. calib.1–3) and a subject-specific knee joint geometry model. The reported data in (a,b) are from the stance phase with 0% being heel-strike and 100% toe-off events. (Online version in colour.)

Figure 6.

(a) Experimental, minimally adjusted and predicted (i.e. psoas and iliacus) excitations for eight representative MTUs including: soleus (sol), gastrocnemius lateralis (gaslat), vastus medialis (vasmed), vastus lateralis (vaslat), biceps femoris long head (bicfemlh), semimembranosus (semimem), psoas and iliacus. Data are from walking trials. (b) The reported joint moments are the experimental, those predicted using minimally adjusted excitations (adj. EMG), and those predicted using only experimental excitations (i.e. EMG-linear envelopes). The reported data are from the stance phase with 0% being heel-strike and 100% toe-off events. (Online version in colour.)

5. Discussion and conclusion

This paper has presented recent methods and technologies that advance the state of the art for modelling the musculoskeletal system across the spatial (macro to micro for muscle and bone) and temporal scales (0.5 s for muscle signals and months for bone remodelling); and storing these using efficient ontologies and tools (such as the MAP). Population-based modelling is an efficient method to rapidly generate individual morphology from only a few measurements and to learn from the ever-increasing supply of imaging data available. Efficient mechanostatistical methods coupling different numerical methods across the spatial scales such as micro-level particle-based methods with solid continuum whole joints may help bridge the scales for use in the clinic. The importance that muscles play in bone remodelling stimuli is highlighted to show that without muscles we often overestimate bone loading since muscles effectively distribute and reduce peak loads across bone. The latest EMG-assisted techniques reveal underlying muscle synergies that can be used to derive a reduced set of muscle primitives. These EMG-based methods have provided the best predictions of knee joint contact force to date in the ‘Grand Knee Challenge’ [12,13], the current gold standard for testing muscle force prediction methods. Our proposal is that, in order to have a clinically relevant VPH, (i) bone and muscle mechanics must be considered together; (ii) models should be trained on population data to permit rapid generation and use underlying principal modes that describe both muscle patterns and morphology; and (iii) these tools need to be available in an open-source repository that the scientific community may use, personalize and contribute to.

Regarding population-based models, there is tremendous potential in the use of population statistics coupled with computational models of the musculoskeletal system to address clinical problems. However, we must first overcome several challenges before population models will have clinical impact. Firstly, streamlining collection and generation of large sets of geometric and functional data (the whole femur in §1 was trained on 300 + CT datasets). Secondly, storing, searching and sharing large datasets; and thirdly, integration into computational modelling frameworks. The MAP is a start in this direction, which will gain traction with more contributions from the scientific community.

Remodelling of biological tissues including bone has always been a challenge to validate in vivo and before microstructural models of bone can be used as part of clinical trials we need more double-blinded studies involving computational simulation integrated with human and animal models. Two recent successful examples include a micro-finite-element model that predicted strength in bone following anabolic fluoride treatment in post-menopausal women as part of a double-blinded clinical study [61], and a micro-finite-element bone remodelling prediction validated against mechanically stimulated murine bone in vivo [35]. Such studies will present the clinical community with more confidence in computational predictions of bone treatments so that they may play a role in pilot testing and to inform the direction of large clinical trials.

The challenge of multiscale continuum muscle models is simultaneously simulating all effects in a multi-spatial and multi-physics framework. A number of key features will need to be included such as biophysical models of the motor neurons, a chemo-electro-mechanical skeletal muscle model, EMG models for predicting the resulting signals, an FES model, and the inverse problem of detecting changes in the mechanical properties of the underlying tissue due to stimulation. Such an integrated model is computationally extremely demanding and requires the use of high-performance computing environments. Furthermore, one should note that all of the above-described models focus on a single skeletal muscle and its neural control. The computational effort multiplies by several orders of magnitude if these models are used to describe parts of the musculoskeletal system. Nevertheless, building up such detailed biophysical models has a tremendous value as these models not only provide a significant advancement in understanding the complex neuromuscular system and valuable input for coarse-scale models, but also provide in silico test environments to identify mechanisms of neuromuscular disorders.

EMG-assisted modelling methodologies address the muscle redundancy problem by making no assumptions on how muscles activate and share the load about a joint. In this context, predictive models based on muscle synergies and modularity enable further opportunities for reducing the neuromuscular indeterminacy of movement and for predicting EMG excitations for those muscles that are hard to measure. Importantly, the EMG-assisted modelling formulations presented in this article allow musculoskeletal simulations to be generated that are consistent both with movement electrophysiological function and with mechanical function, something central for extracting realistic muscle force solutions. This all opens up new avenues for characterizing human neuromusculoskeletal function across individuals and conditions and for developing personalized rehabilitation treatments that ultimately enhance human health.

To summarize how the presented methods may be used to influence personalized human health, a clinical example encompassing all computational frameworks outlined within this work can be found in the field of neuro-prosthetics. The shape and geometry of the muscle is essential for identifying an optimally designed socket for a particular subject-specific residual limb. The design of an optimal socket is influenced not only by the residual limb's geometry but also by muscular activity. Since muscle activation changes the material behaviour of a residual limb during movement, knowing the muscle's activation through multiscale EMG-informed skeletal muscle modelling can tremendously improve the design. Furthermore, EMG-based modelling can identify subject-specific neuromuscular activity after amputation and therefore help to better design, train and control a neuroprosthesis. Moreover, predicting the muscular activity within a subject-specific limb and the distribution of the weight of the socket provides the clinician with a predictive tool to potentially identify pressure points (stress peaks within the bone) and, hence, information on areas in which pressure ulcers are likely to develop. Using the bone remodelling simulations for predicting the long-term changes within the bone provides additional information for designing an optimal socket that prevents excessive bone loss due to the additional ‘artificial’ system. The right prosthesis can maintain homeostasis with respect to muscular mass and optimal mechanical performance of the artificial limb (and not only with respect to all its single components but also at the human–artificial limb interface).

Authors' contributions

J.F. wrote §2 and coordinated the manuscript text and figures; J.Z. and T.B. wrote §1; T.H. and O.R. wrote §3; and M.S. and D.L. wrote §4. All authors contributed to the introduction and discussion and gave final approval for publication.

Competing interests

The authors have no competing interests.

Funding

We received no funding for this study.