Impact of Host Heterogeneity on the Efficacy of Interventions to Reduce Staphylococcus aureus Carriage

Abstract

Background

Staphylococcus aureus is a common cause of bacterial infections worldwide. It is most commonly carried in and transmitted from the anterior nares. Hosts are known to vary in their proclivity for S. aureus nasal carriage and may be divided into persistent, intermittent, and non- carriers depending on duration of carriage. Mathematical models of S. aureus to predict outcomes of interventions have however typically assumed that all individuals are equally susceptible to being colonized.

Objective

To characterize biases created by assuming a homogeneous host population in estimating efficacy of control interventions

Design

Mathematical modeling

Methods

We developed a model of S. aureus carriage in the healthcare setting under the homogeneous assumption as well as a heterogeneous model to account for the three types of S. aureus carriers. In both models, we calculated the equilibrium carriage prevalence to predict the impact of control measures (reducing contact and decolonization).

Results

The homogeneous model almost always underestimates S. aureus transmissibility and overestimates the impact of intervention strategies in lowering carriage prevalence compared to the heterogeneous model. This finding is generally consistent regardless of changes in model setting to vary the proportions of various carriers in the population and the duration of carriage for these carrier types.

Conclusions

Not accounting for host heterogeneity leads to systematic and substantial biases in predictions of the effects of intervention strategies. Further understanding of the clinical impacts of heterogeneity through modeling can help to target control measures and allocate resources more efficiently.

Introduction

Staphylococcus aureus is a common cause of bacterial infections worldwide ¹, causing a range of diseases including community-acquired soft tissue infections and nosocomial infections. The majority of carriage episodes are asymptomatic, and this is the population responsible for transmission ². While multiple body sites can be colonized, the most frequent carriage site for S. aureus is the anterior nares: approximately one-third of healthy individuals asymptomatically carry S. aureus in this location at any given point in time ^3,4.

Longitudinal studies have shown that the probability and duration of S. aureus nasal carriage vary. Typically such studies have classified participants into three host classes: persistent carriers, defined as those in whom carriage lasts for many months (about 20% of the adult population); intermittent carriers, defined as individuals who harbor S. aureus intermittently (about 30% of the adult population); and non-carriers, who almost never carry S. aureus (about 50% of the adult population)^5–7. While this classification is somewhat arbitrary (as “persistence” for example, will depend on length of follow-up), it is a convenient summary of the observed heterogeneity. In such a population, an individual observed as a carrier may be either a persistent or an intermittent carrier, while a non-carrier at a particular moment may be either a non-carrier or an intermittent carrier.

Reduction of S. aureus transmission by interventions including hand hygiene, isolation, and decolonization reduces the incidence of nosocomial infections ^8,9. To examine the effectiveness of these interventions and the transmission dynamics of the pathogen, several mathematical models have been developed ^10–18. These models have assumed a homogenous population in which all individuals are equally susceptible to colonization. This assumption is clearly incorrect, and the failure to discriminate between hosts that are highly resistant to colonization and those that may play a disproportionate role in transmission may alter the predicted impact of control strategies.

We show here that assuming a homogeneous population causes systematic and substantial biases in model outcomes and illustrate how incorporation of a heterogeneous host population changes the predictions of the model. In particular, homogeneity assumptions tend to underestimate transmissibility and overestimate the impacts of control interventions.

Methods

Model Description

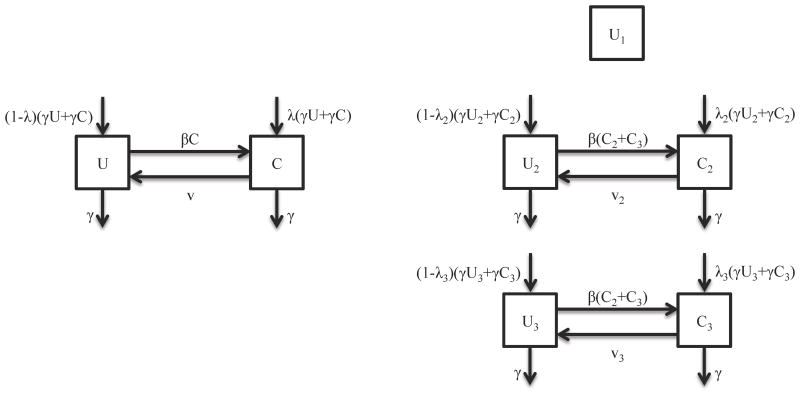
We used a deterministic SIS (susceptible-infected-susceptible)-type transmission model of S. aureus colonization in the healthcare setting, though we use U (uncolonized) and C (colonized) to emphasize that we are tracking colonization not infection (Figure 1). The proportions of colonized and uncolonized patients for any time t, U(t) and C(t), sum to 1. The transmission parameter, β, is the rate at which hosts contact each other and transmit per unit time and v is the natural rate with which S. aureus is cleared per unit time, both of which in the homogenous case are assumed to be the same for all patients. We assumed that the discharge rate, γ, is the same for uncolonized and colonized patients and that the number of patients remains fixed such that the admission rate equals the discharge rate. In addition, the probability that an individual is colonized at admission is λ. The transmission model in the homogeneous case is then given by the following differential equations:

Figure 1.

Transmission models of S. aureus colonization for (a) the homogeneous model and (b) the heterogeneous model. The diagram shows the inflow and outflow of uncolonized and colonized patients (U, C). Subscripts indicate each of the three host classes (non-carriers, intermittent carriers, and persistent carriers).

$$\dot{U}=\left(1-\lambda \right)\left(\gamma \mathrm{U}+\gamma \mathrm{C}\right)-\beta \mathrm{U}\mathrm{C}+\text{v}\mathrm{C}-\gamma \mathrm{U}$$

$$\dot{\mathrm{C}}=\lambda \left(\gamma \mathrm{U}+\gamma \mathrm{C}\right)+\beta \mathrm{U}\mathrm{C}-\mathrm{v}\mathrm{C}-\gamma \mathrm{C}\mathrm{or}\mathrm{C}=1-\mathrm{U}$$

For comparison, we analyzed a stratified version of the transmission model that incorporates host heterogeneity. Let N₁, N₂, and N₃ be the proportion of the population who are non-carriers, intermittent carriers, and persistent carriers. In each of these groups, a proportion U₁(t), U₂(t), U₃(t) (of the entire population) is uncolonized at any moment, and proportions C₂(t) and C₃(t) are the respective proportions colonized (there is no C₁ category since this part of the population is highly resistant to colonization). Then N₁=U₁; N₂=U₂+C₂, and N₃=U₃+C₃. We also model heterogeneity such that v₂ and v₃ are the natural rate at which S. aureus is cleared per unit time from an intermittent carrier and a persistent carrier, respectively. In addition, λ₂ is the probability that an intermittent carrier is colonized at admission while λ₃ is the probability that a persistent carrier is colonized at admission. While studies have shown that persistent carriers have higher risk of infection, the colonization rate in different nasal carrier types remains unknown ^19,20. Given the limited data on the transmission parameter, we assumed that intermittent carriers and persistent carriers have the same per capita rate of effective contact; hence the transmission parameter β is the same. This model is given by the following system of differential equations:

$${\dot{\mathrm{U}}}_2=\left(1-{\lambda }_2\right)\left(\gamma {\mathrm{U}}_2+\gamma {\mathrm{C}}_2\right)-\beta {\mathrm{U}}_2\left({\mathrm{C}}_2+{\mathrm{C}}_3\right)+{\mathrm{v}}_2{\mathrm{C}}_2-\gamma {\mathrm{U}}_2$$

$${\dot{\mathrm{C}}}_2={\lambda }_2\left(\gamma {\mathrm{U}}_2+\gamma {\mathrm{C}}_2\right)+\beta {\mathrm{U}}_2\left({\mathrm{C}}_2+{\mathrm{C}}_3\right)-{\mathrm{v}}_2{\mathrm{C}}_2-\gamma {\mathrm{C}}_2$$

$${\dot{\mathrm{U}}}_3=\left(1-{\lambda }_3\right)\left(\gamma {\mathrm{U}}_3+\gamma {\mathrm{C}}_3\right)-\beta {\mathrm{U}}_3\left({\mathrm{C}}_2+{\mathrm{C}}_3\right)+{\mathrm{v}}_3{\mathrm{C}}_3-\gamma {\mathrm{U}}_3$$

$${\dot{\mathrm{C}}}_3={\lambda }_3\left(\gamma {\mathrm{U}}_3+\gamma {\mathrm{C}}_3\right)+\beta {\mathrm{U}}_3\left({\mathrm{C}}_2+{\mathrm{C}}_3\right)-{\mathrm{v}}_3{\mathrm{C}}_3-\gamma {\mathrm{C}}_3$$

Our goal here was to examine the impact of including carriage heterogeneity by comparison with a homogeneous model.

Parameter Estimates

We used median S. aureus nasal survival time of 14 days among intermittent carriers and >154 days among persistent carriers ²¹ as the average carriage duration to parameterize the clearance rates, v₂ and v₃, in the heterogeneous model (Table 1). We used the average median S. aureus nasal survival times for the various carrier types (0.30*14 + 0.20*154 = 35 days) to parameterize the clearance rate, v, in the homogeneous model. Furthermore, we used an average length of stay of 7 days ¹³ to parameterize hospital discharge rate.

Table 1. Description of model parameters for the homogeneous and heterogeneous models of S. aureus carriage.

Model	Parameter	Value	Description
Homogeneous	β	$\lambda =\frac{\mathrm{C}}{\mathrm{U}+\mathrm{C}}$: 0.028 day-1 λ = 0: 0.232 day-1	Transmission parameter
	v	ln(2)/35 day-1	Natural clearance rate
	γ	7 days-1	Discharge rate
Heterogeneous	β	${\lambda }_{\mathrm{i}}=\frac{{\mathrm{C}}_{\mathrm{i}}}{{\mathrm{U}}_{\mathrm{i}}+{\mathrm{C}}_{\mathrm{i}}}$: 0.115 day-1 λi = 0: 0.866 day-1	Transmission parameter assuming 20% persistent, 30% intermittent, and 50% non- carriers (Figure 2)
	β*	${\lambda }_{\mathrm{i}}=\frac{{\mathrm{C}}_{\mathrm{i}}}{{\mathrm{U}}_{\mathrm{i}}+{\mathrm{C}}_{\mathrm{i}}}:\frac{{\mathrm{x}}_2{\beta }^{\ast }}{0.3{\beta }^{\ast }+{\mathrm{v}}_2}+\frac{{\mathrm{x}}_3{\beta }^{\ast }}{0.3{\beta }^{\ast }+{\mathrm{v}}_3}$ ${\lambda }_{\mathrm{i}}=0:1=\frac{{\mathrm{x}}_2{\beta }^{\ast }}{0.3{\beta }^{\ast }+{\mathrm{v}}_2+\gamma }+\frac{{\mathrm{x}}_3{\beta }^{\ast }}{0.3{\beta }^{\ast }+{\mathrm{v}}_3+\gamma }$ (x2 and x3 are the proportions of intermittent and persistent carriers)	Transmission parameter for 30% overall carriage prevalence in populations with varying proportions of carrier classes (Figure 3)
	v2	ln(2)/14 day-1	Natural clearance rate for intermittent carriers
	v3	ln(2)/154 day-1	Natural clearance rate for persistent carriers
	γ	7 days-1	Discharge rate

Empirical observations show a 30% prevalence of S. aureus carriage in multiple settings ²². We used this to find the transmission parameter, β, for both models under two extreme scenarios: Scenario A in which the proportion colonized at admission is the same as the proportion of that host class colonized in the inpatient population (λ_i =C_i/(U_i+C_i)) and Scenario B in which all individuals are uncolonized at admission (λ_i=0). Scenario B can be thought of as an extreme case in which all transmission is limited to the hospital, and the Scenario A as the alternate extreme where either transmission is equally intense outside and inside the hospital or where individuals are very rapidly readmitted after discharge. Alternatively, Scenario A can also be thought of as a model for a community in which the population of hosts does not appreciably change over the time scale that would be considered in an intervention study (months to a few years).

Modeling Interventions

We considered two classes of control measures. The first aims to reduce the contact rate and thus the transmission parameter β through isolation of carriers or other infection control measures such as handwashing. The second class of control measures is targeted at decolonizing carriers, such as through intranasal application of mupirocin alone or with antiseptic soaps or antimicrobial agents. This is modeled through the parameter δ, the rate of successful decolonization. In both the homogeneous and heterogeneous model, we calculated the new equilibrium carriage prevalence after the implementation of control measures (reducing β or varying δ). We examined the impact of interventions on carriage prevalence when varying the proportions of carrier types and the durations of persistent and intermittent carriage. All equilibrium prevalence predictions were calculated analytically and graphed using R.

Results

Heterogeneous carriage reduces the expected impact of interventions

In Scenario A where those colonized at admission is the same as the proportion colonized among that host class (λ_i=C_i/(U_i+C_i)), the homogeneous model predicts that even a modest reduction in β through interventions aimed at contact rates has a marked impact on carriage prevalence (Figure 2a). A 30% reduction in β is expected to eliminate S. aureus from the population. In contrast in the heterogeneous model, elimination requires reducing β by more than 80%. Similarly, the homogeneous model predicts that decolonization every 120 days or so will almost eliminate carriage, whereas the same regime applied to the heterogeneous population will have very little effect (Figure 2b).

Figure 2.

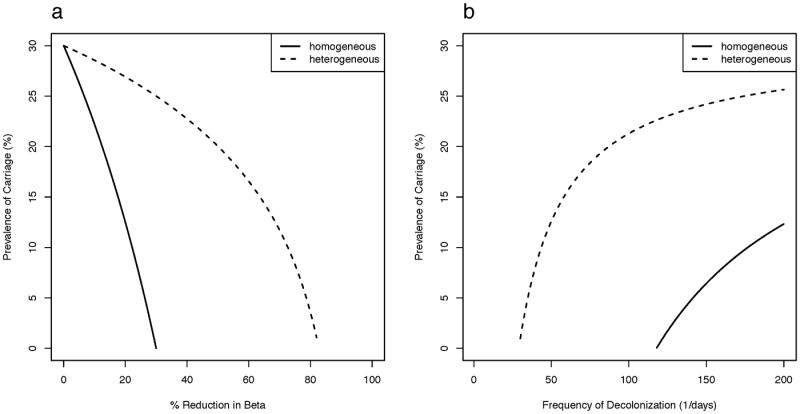
Impact of interventions of (a) reducing contact and (b) decolonization on S. aureus carriage prevalence under the homogeneous model and the heterogeneous model assuming three hosts classes (20% persistent, 30% intermittent, and 50% non- carriers) and that only uncolonized individuals are admitted into the hospital. In both models, 30% carriage prevalence is assumed in absence of any interventions.

In Scenario B where all individuals are uncolonized at admission (λ_i=0), the homogeneous model consistently overestimates the prevalence of overall carriage for both types of interventions, but to a lesser degree than Scenario A. Reducing β by approximately 30% is expected to eliminate S. aureus in the homogeneous model while the same outcome in the heterogeneous model requires reducing β by approximately 60% (Figure 3a). Under this scenario, decolonization strategies have little impact on reducing S. aureus carriage in both models, and in the heterogeneous model, it becomes almost impossible to eliminate carriage.

Figure 3.

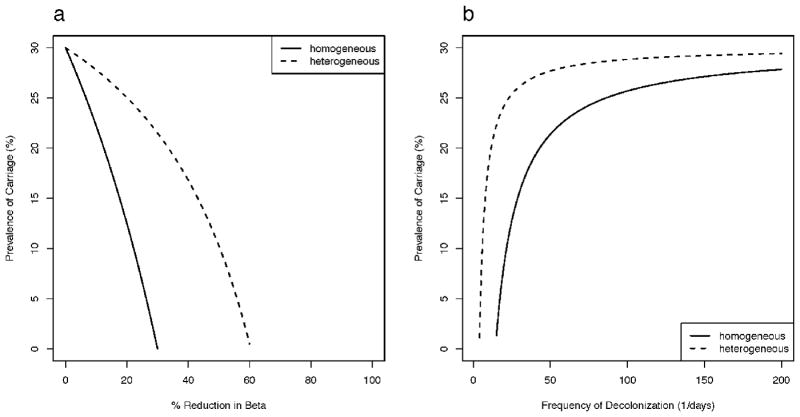
Impact of interventions of (a) reducing contact and (b) decolonization on S. aureus carriage prevalence under the homogeneous model and the heterogeneous model assuming three hosts classes (20% persistent, 30% intermittent, and 50% non- carriers) and that hospital admission of those colonized is the proportion colonized among that host class. In both models, 30% carriage prevalence is assumed in absence of any interventions.

The impact of varying the proportion of carrier classes in the host population

The exact proportions of persistent, intermittent, and non- carriers have been studied in only a few populations ^5,22 and may vary in different settings. We hence examined how varying the population composition impacts carriage prevalence. In Scenario B, we compared the results of models with different proportions of host classes relative to the homogeneous model as a ratio of equilibrium carriage prevalence after a 25% reduction in the β* parameter or a decolonization regime every 6 months (δ = 1/180 day^-1). For interventions targeting transmission, all distributions of heterogeneous populations resulted in higher equilibrium prevalence compared with the homogeneous model with the largest proportions of non-carriers giving the highest ratio of roughly 4.25 (Figure 4a). For intervention based on decolonization, the carriage prevalence in the heterogeneous model was at worst 3-fold higher compared to the homogeneous model (Figure 4b). An exception to the otherwise general finding that incorporating heterogeneity reduces the predicted impact of interventions is found in populations where 40-45% are persistent carriers (the contour line with ratio=1 in Figure 4b). Here, decolonization in the heterogeneous model is more effective compared to the homogeneous model and the effect is markedly increased as the proportion of persistent carriers increases beyond this threshold. In Scenario A, all distributions of heterogeneous populations consistently predicted higher equilibrium prevalence compared with the simple model for both interventions (Figure S1). For both scenarios, the distributions of hosts that we predict will have the largest negative impact on the effectiveness of both interventions was close to the range of proportions of different host classes reported in longitudinal studies ^5,6,22.

Figure 4.

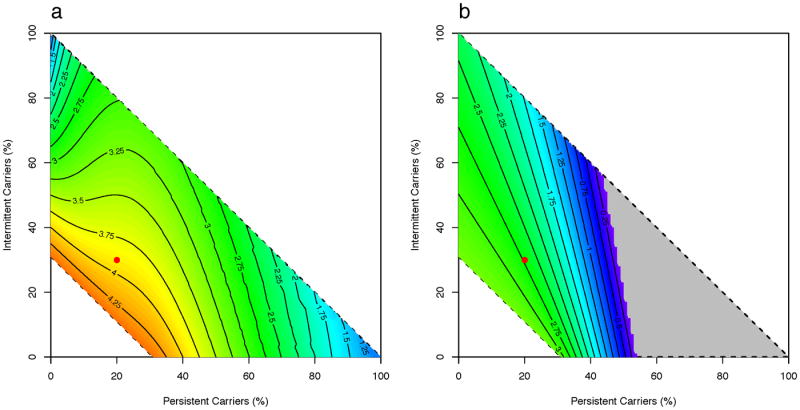
A heat-map of the ratios of carriage prevalence in the heterogeneous model to the homogeneous model when varying proportions of carrier classes under Scenario A (admission of those colonized is the proportion colonized among that host class) with intervention of (a) reducing β* parameter (see Table 1) by 25% and (b) setting δ parameter to 1/180 day^-1. The ratio represents the magnitude of difference between the models, with >1 indicating that the heterogeneous model predicts higher carriage prevalence compared to the homogeneous model. The dotted lines enclose all possible combinations of the proportions of persistent, intermittent, and non- carriers. Complete elimination of S. aureus carriage in the heterogeneous model is shown in grey. The red dot represents assumed proportions of each carrier type for the initial analysis.

The impact of varying the duration of colonization

We also examined the impact of varying the duration of colonization, and hence potential transmission, among the different classes of host assuming all individuals are uncolonized at admission (Scenario B) using the same intervention parameters as above. Again the homogeneous model is consistently overoptimistic. As shown in Figure 5a, the heterogeneous model predicted carriage prevalence roughly 4 times that of the homogeneous model and this is robust to the durations of intermittent and persistent carriage. Similarly as shown in Figure 5b, decolonizing individuals every six months was more effective in reducing the prevalence of overall carriage as predicted in the homogeneous model compared to that of the heterogeneous model, regardless of the durations of carriage assumed. Similarly, the finding that the heterogeneous model predicts higher equilibrium carriage prevalence compared to the homogeneous model regardless of durations of persistent and intermittent carriage for both interventions is also observed in Scenario A (Figure S2).

Figure 5.

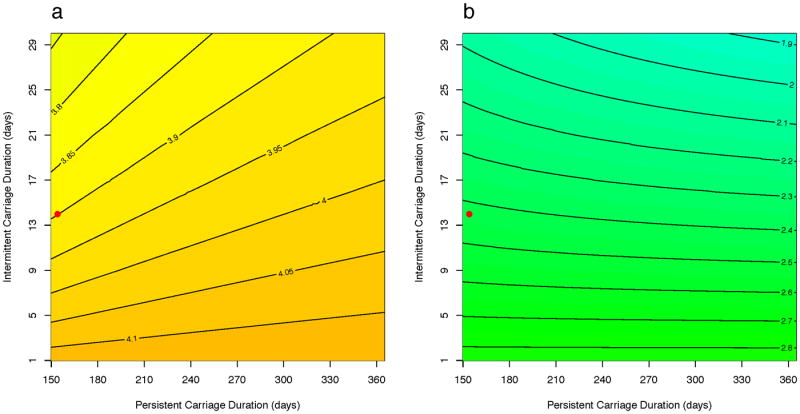
A heat-map of the ratios of carriage prevalence in the heterogeneous model to the homogeneous model when varying persistent and intermittent carriage durations under Scenario A (admission of those colonized is the proportion colonized among that host class) with intervention of (a) reducing β* parameter (see Table 1) by 25% and (b) setting δ parameter to 1/180 day^-1. The ratio represents the magnitude of difference between the models, with >1 indicating that the heterogeneous model predicts higher carriage prevalence compared to the homogeneous model. The red dot represents assumed carriage durations of each carrier type for the initial analysis.

Discussion

Mathematical models of S. aureus transmission can quantitatively predict outcomes of interventions and guide decision-making ^{13–18,23,24}. These models have made the assumption that all individuals have the same probability and duration of carriage. This is often supported by the notion that variation in susceptibility is considered to result in smaller outbreaks ²⁵ and therefore models assuming equal susceptibility are considered the worst-case scenario in the sense of the extent of transmission they produce ²⁶. However, this perception does not account for the fact that a model ignoring heterogeneity in the population will be “fooled” by the overall low prevalence of colonization into underestimating the transmissibility of the pathogen. In turn, the lower estimate of transmissibility can lead to an overestimate of the estimated impact of interventions.

We have examined two scenarios that represent two extremes of time between hospital admissions. Scenario B where only uncolonized individuals are admitted simulates a very long, or even infinite, time between admissions while Scenario A where newly admitted patients are assumed to be colonized in the proportion that would be expected for hosts of that class simulates a feedback loop in which people are frequently readmitted. Mathematically, the latter scenario is equivalent to a model of community-acquired S. aureus. In both scenarios, the homogeneous assumption consistently overestimates the effectiveness of control strategies. Moreover, this observation was robust to the proportions of carrier types and the carriage duration for each type. The exception was when persistent carriers make up 40-45% of the population or more, the heterogeneous model made the opposite prediction: decolonization would reduce carriage more than one would assume from the homogeneous model. This reflects the disproportionate contribution of the persistent carriers to transmission as a result of being colonized for a longer period.

Other studies have considered the effects of heterogeneity on the spread of sexually-transmitted ²⁷ and vector-borne ²⁸ infections. These studies have in common the idea that the existence of particularly high-risk hosts contributes disproportionately to transmission. The key issue in both cases is that such hosts are simultaneously more likely to become infected and to transmit infection, as the same activity (being bitten or sex) is necessary for both. In these settings, the basic reproductive number (R₀) is proportional to the sum of the mean and the variance/mean ratio for sexual activity or rate of being bitten in simple models of heterogeneous host populations. We have considered and analyzed a different phenomenon here. In our model, hosts differ in their durations of carriage, which affects transmission but not acquisition rate (and we assume that all hosts are equally likely to become colonized, though some may have effectively zero duration). In this setting, the R₀ is a simple average of the transmission from the different types of hosts, weighted by the frequency of each host type and the carriage duration in that host type. In our heterogeneous model, the non-carriers are not capable of transmitting, and persistent or intermittent carriers are colonized at a faster rate and naturally decolonize at a slower rate. The consequence of this is an increase of R₀. Thus ignoring heterogeneity leads us to underestimate transmissibility and overestimate an intervention's effectiveness.

Our models do not take into account factors such as antibiotic resistance, compliance with interventions, environmental or healthcare related transmission. We developed our models to demonstrate the biases created by the failure to incorporate heterogeneity in carriage types. Our analysis is deliberately focused on variation arising from susceptibility and duration of carriage, but this is only one possible source of heterogeneity. Alternatively, hosts may be equally susceptible, but vary in their ability to transmit. This has been experimentally observed in finger-finger transmission of enterococci ²⁹. Host susceptibility may be a general issue in nosocomial epidemiology across different bacteria species and colonization sites.

Improved understanding of host heterogeneity in carriage through modeling may significantly change ways in which dynamics of colonization and disease are characterized, as well as the approaches for implementing control measures. In a randomized clinical trial ³⁰, findings of limited reduction in methicillin-resistant S. aureus carriage despite decolonization with mupirocin may be explained in part by our analysis, which predicts the effort required to achieve control is greater than expected. We also note that strategies that might be particularly effective in one setting may not directly translate to another setting where the population may have a different distribution of carrier types. Future work to understand the mechanisms underlying the heterogeneity in S. aureus carriage will aid in targeted interventions that ensure optimal allocation of resources.