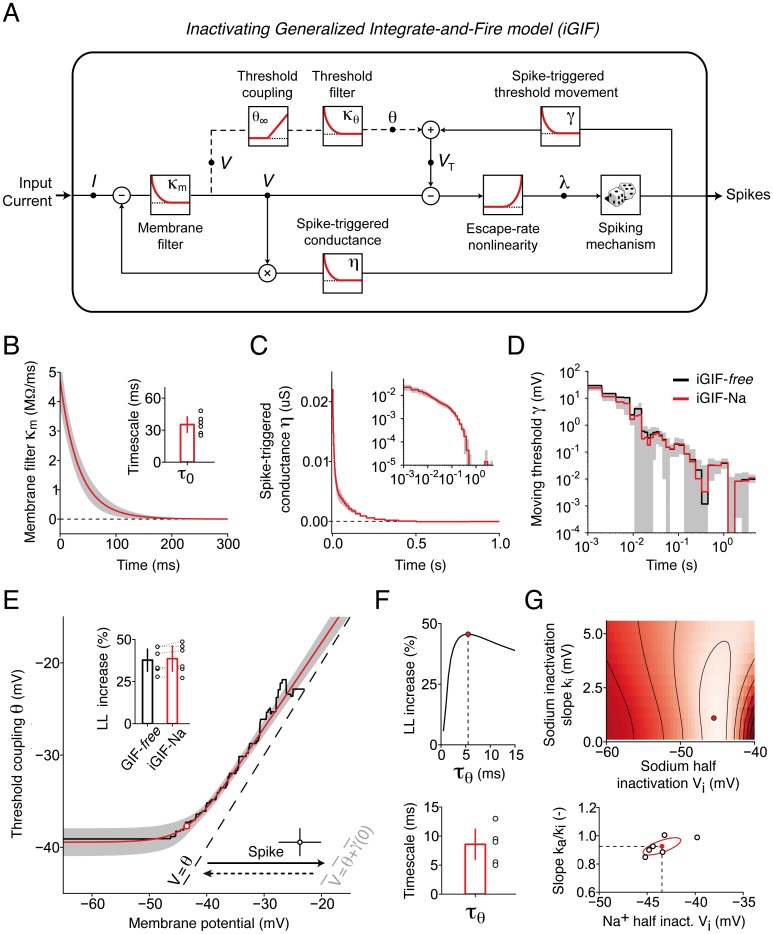
Fig 4. iGIF model with parameters extracted from intracellular recordings.

(A) Schematic representation of the iGIF model. The input current is first low-pass filtered by the Passive membrane filter ${\kappa }_{\text{m}}\left(t\right)=\Theta \left(t\right)C^{-1}{e}^{-\frac{t}{{\tau }_{\text{m}}}}$. The resulting signal models the subthreshold membrane potential V(t) and, after subtraction of the firing threshold V_T(t), is transformed into a firing intensity λ(t) by the exponential Escape-rate nonlinearity. Spikes are emitted stochastically and elicit both a Spike-triggered conductance η(t) and a Spike-triggered threshold movement γ(t). In the iGIF model, but not in the GIF model, the firing threshold V_T(t) is coupled to the subthreshold membrane potential (dashed circuit). For that, the membrane potential V(t) is first passed through the nonlinear Threshold coupling function θ_∞(V) and then low-pass filtered by the Threshold filter ${\kappa }_{\theta }\left(t\right)=\Theta \left(t\right){\tau }_{\theta }^{-1}{e}^{-\frac{t}{{\tau }_{\theta }}}$. (B)-(E) Average parameters extracted from 6 Pyr neurons. Black: iGIF-free, red: iGIF-Na. Gray areas indicate one standard deviation across cells for the iGIF-Na model. (B) Passive membrane filter κ_m(t). Inset: passive membrane timescale τ_m. Open circles: results from individual cells. Bar plot: mean and standard deviation. (C) Spike-triggered conductance η(t). Inset: same data on log-log scales. (D) Spike-triggered threshold movement γ(t). (E) Nonlinear threshold coupling θ_∞(V) (iGIF-free, solid black line; iGIF-Na, solid red line). Spikes are emitted stochastically when the spiking boundary V = V_T is approached. This boundary defines the line where the probability p of emitting a spike during a time bin of ΔT = 0.1 ms reaches p = 0.63. To the right, the probability increases further. In the absence of previous action potentials, the spiking boundary is given by V = θ (dashed black). After an action potential, the spiking boundary instantaneously shifts to the right by γ(0)≈25 mV (dashed gray), and then slowly decays back to V = θ. After each spike, the variables (V(t), θ(t)) are reset to $(V_{\text{reset}},V_T^{*})$ (open circle; error bars denote one standard deviation across cells). The open red circle indicates the Na⁺ half-inactivation voltage V_i, where the threshold becomes sensitive to the membrane potential. Inset: percentage increase in model log-likelihood (LL) of iGIF models with respect to the GIF model. Open circles: model performance on the same cell for iGIF-free and iGIF-Na. Bar plots: mean and standard deviation across neurons. (F) Top: LL percentage increase of the iGIF-free model as a function of τ_θ. Red circle: optimal timescale τ_θ. Data are shown from a typical neuron. Bottom: optimal timescales τ_θ extracted from 6 Pyr neurons. (G) Top: LL percentage increase of the iGIF-Na model as a function of k_i and V_i. The LL increases from dark to light red. Red circle: optimal parameters. Bottom: optimal parameters extracted from 6 different Pyr neurons. Note that the half-inactivation voltages V_i reported in the figure are positively biased due to uncompensated liquid junction potential of 14.5 mV (see Materials and Methods). The mean and the standard deviational ellipse across cells are shown in red.