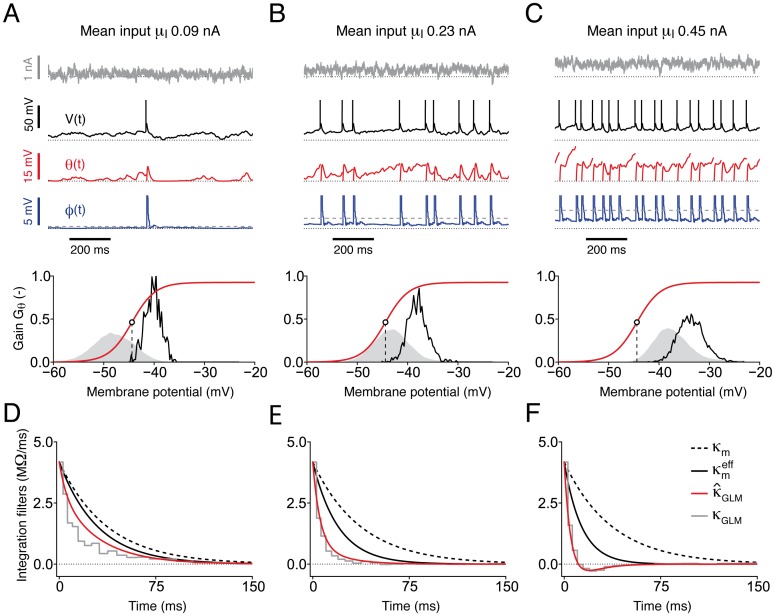
Fig 7. The threshold-voltage coupling progressively activates with increasing input strengths μ_I.

Dynamics of the iGIF model (with parameters extracted from a typical Pyr neuron) responding to three fluctuating currents with standard deviation σ_I = 100 pA, temporal correlation τ_I = 3 ms and μ_I = 90 pA (panels A and D), μ_I = 230 pA (panels B and E) and μ_I = 450 pA (panels C and F). (A) Top: input current I(t) (gray), membrane potential V(t) (black), voltage-dependent threshold adaptation θ(t) (red) and spike-dependent threshold adaptation $\varphi \left(t\right)={\sum }_{\widehat{t}}\gamma (t-\widehat{t})$ (blue) as a function of time. The four dotted lines indicate: I = 0 nA, V = E_L, $\theta =V_{\text{T}}^{*}$ and φ = 0 mV. Bottom: distribution of subthreshold membrane potential fluctuations P(V) (gray) and of voltages at which spikes were initiated P(V|spike) (black). The instantaneous threshold-coupling gain $G_{\theta }\left(V\right)=\frac{d}{dV}{\theta }_{\infty }^{\text{Na}}\left(V\right)$ (red) defines the sensitivity of the firing threshold to the membrane potential and can be interpreted as an activation function for the threshold-voltage coupling. Since ${\theta }_{\infty }^{\text{Na}}\left(V\right)$ is a nonlinear function of V, G_θ depends on the membrane potential. For low inputs, the histogram of voltage s P(V) covers mostly the region V ≤ V_i (dashed horizontal line), where the threshold-voltage coupling is not active. (B) Same results as in panel A obtained by increasing the mean input μ_I. With medium input strength, the majority of the voltage distribution lies in the region V ≈ V_i, where the threshold-voltage coupling is active. (C) As in panel B, but for strong mean input μ_I. In this case, the voltage-threshold coupling is almost always active (i.e., V ≥ V_i). (D) The GLM integration filter κ_GLM(t) (solid gray) obtained by fitting a GLM to the spiking activity of the iGIF model (panel A) is compared against the passive membrane filter κ_m(t) (dashed black, see Fig 4B) and the effective membrane filter ${\kappa }_{\text{m}}^{\text{eff}}\left(t\right)$ (solid black), which accounts for the conductance increase mediated by η. The GLM integration filter κ_GLM(t) (solid gray) matches the theoretical filter ${\widehat{\kappa }}_{\text{GLM}}\left(t\right)$ (solid red; see Eq 7), which takes into account the effect of the threshold-voltage coupling. (E)-(F) Same plots as in panel D, but for increased mean input μ_I.