Fig. 6. Acoustic realizations of superlens and hyperlens.

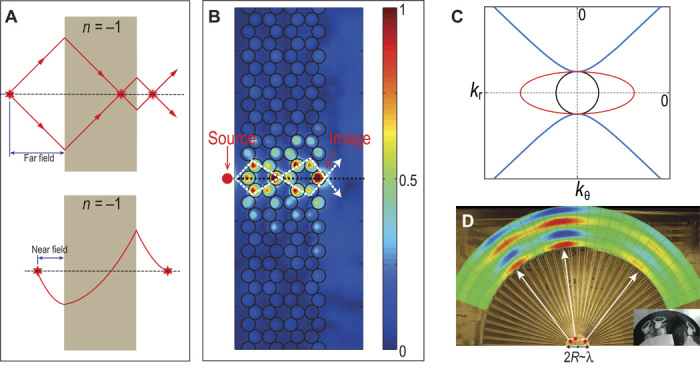
(A) Top: A slab of doubly negative medium can bring diverging waves into two foci: one inside the slab, and the other one outside. Bottom: The same slab can amplify evanescent waves, thereby theoretically enabling the formation of a perfect image. (B) Experimental demonstration of the imaging capability of an acoustic superlens (30). Here, cavity resonators (soda cans, represented by black circles) were arranged into a honeycomb lattice. It is clearly seen that the near field was sustained and even amplified by the metamaterial slab. Negative refraction and the consequent foci are delineated by white dashed arrows. The normalized pressure intensity field is displayed as a color map. The source (red dots) had an amplitude full width at half maximum of λ/5, whereas the measured image size was λ/15. (C) Three distinctive equifrequency contours. The black circle represents that of a homogeneous material. Anisotropy along $\widehat{\mathit{r}}$ and $\widehat{\mathbf{\theta }}$ can distort the contour into an ellipse (red), in which a large k_r can be accessed. However, if the material’s parameter is negative along $\widehat{\mathbf{\theta }}$ but positive along $\widehat{\mathit{r}}$, then the contour becomes hyperbolic, wherein k_r and k_θ are no longer bounded (blue curves). (D) The strong anisotropy in k_r and k_θ, such as that indicated by the red ellipse in (C), used for superresolution imaging, as shown experimentally in Li et al. (63). Here, the fan-like structure has stripes alternating between air and brass. From the effective medium theory, the effective mass is highly anisotropic along the $\widehat{\mathit{r}}$ and $\widehat{\mathbf{\theta }}$ directions. The center circle of the device has a diameter of about one wavelength, in which three sound sources were closely placed with subwavelength separations, represented by the red dots. An image of the sound sources is also shown in the lower-right inset. Red/blue represents positive/negative pressure, with the three clearly resolved regions being representative of the magnified image of the three sound sources.