Self-propulsion and interactions of catalytic particles in a chemically active medium

Abstract

Enzymatic “machines,” such as catalytic rods or colloids, can self-propel and interact by generating gradients of their substrates. We theoretically investigate the behaviors of such machines in a chemically active environment where their catalytic substrates are continuously synthesized and destroyed, as occurs in living cells. We show how the kinetic properties of the medium modulate self-propulsion and pairwise interactions between machines, with the latter controlled by a tunable characteristic interaction range analogous to the Debye screening length in an electrolytic solution. Finally, we discuss the effective force arising between interacting machines and possible biological applications, such as partitioning of bacterial plasmids.

I. INTRODUCTION

The interior of a living cell is a nonequilibrium medium that continuously produces and destroys high-energy molecules. These high-energy “solute” molecules may be bound and processed by enzymatic (biocatalytic) “machines.” Gradients of the solute molecules may a ect the self-organization of these catalytic cellular machines. Intriguingly, the biochemical activity of the underlying medium could alter such gradients, and thus modulate the behavior of these machines.

Self-propulsion and self-organization of catalytic colloidal particles through chemical gradients have previously been explored in synthetic systems without ambient chemical activity. Patterned catalytic particles can self-propel as artificial micro- or nano-motors by generating concentration gradients through chemical reactions at their surfaces [1-9]. Catalytic particles can also self-organize into a variety of nonequilibrium phases by interacting with the chemical gradients generated by other catalytic particles [10-13].

Additionally, the dynamics of protein catalysts (enzymes) can be altered in vitro by the presence of their substrates. Experiments have shown that the diffusion of enzyme molecules is enhanced when enzymes catalyze their substrates and that these molecular machines translocate up substrate gradients toward high substrate concentration [14-17]. These phenomena may have phoretic origins, although the precise mechanisms are not yet fully understood [14-18].

Phoretic effects of this general type are thought to play a role in organizing cellular structures and processes in vivo [19-24]. The cellular interior is a nonequilibrium environment with ambient chemical activity or passive biomolecule degradation, but previous studies have generally only considered an “inert” medium. In an inert environment, the medium itself neither creates nor destroys the substrate required for the machines’ catalytic behavior. However, molecular dynamics simulations have shown that the chemical activity of the underlying environment may alter diffusiophoresis [25, 26]. Those simulations illustrate that background chemical activity can reduce the self-propulsion speed [25]. Here, we analyze how the chemical activity of the environment controls self-propulsion and interactions of catalytically active machines.

In Section II we introduce a simple first-order kinetic model of catalysis by the environment, which immediately leads to a characteristic length scale, λ, set by the balance of solute diffusion and destruction, analogous to the Debye screening length in electrostatics. We investigate phoretic self-propulsion of the machines and find that asymmetric machines self-propel with a velocity that scales in a way that is dependent on the ratio of machine size to λ, as well as other factors. In Section III we analyze the pairwise interactions between machines. The magnitude and range of these interactions is regulated by the screening length found in Section II, and interactions can be tuned to be repulsive or attractive and strong or weak by chemical properties of the medium itself. Additionally, we construct a simulation of discrete solute particles and catalytic machines to demonstrate the validity of our continuous-field approach, and show that an effective potential can be used to describe machine interactions in the appropriate physical regime. In Section IV we discuss the application of our model to a biological subcellular spatial organization problem of current interest, namely the partitioning of plasmid DNA molecules within a bacterium.

II. SELF-PROPULSION

A. Theoretical model

We consider diffusiophoresis of enzymatic particles in a chemically active medium which generates reactant solute at rate k⁺ and destroys it at rate of k⁻c, where c is the local reactant concentration. The system is overdamped; the solute species diffuses with constant D_s, and spherical catalytic particles of radius r₀ diffuse slowly with constant D_c ≪ D_s. The catalytic particles interact with the solute species chemically by creating or destroying solute and physically by attracting or repelling solute. The model predicts that bulk biochemical activity alters self-propulsion and controls the range, strength, and sign of interactions between catalytic particles.

We first analyze the model in the continuum limit for the case of a single catalytic particle. As in the analysis of the inert medium (where k⁺ = k⁻ = 0) in [3], we determine the solute concentration near the catalytic particle. Since D_c ≪ D_s, we assume a steady-state concentration profile. Thus, we solve a reaction-diffusion equation:

$$D_s{\nabla }^{2}c-k^{-}c+k^{+}=0,$$ (1)

which accounts for both diffusion and the chemical activity of the medium.

At the surface of the catalytic particle, we consider two distinct scenarios. In the first, solute concentration is sufficiently high so that the surface catalysis rate is reaction-limited, and thus independent of the local solute concentration [3]. We also consider a diffusion-limited case where the surface catalysis rate grows linearly with local solute concentration; this case only has a nontrivial steady-state in a chemically active medium. These cases correspond to two different boundary conditions:

$${\phantom{\mid }-\widehat{r}{D}_s\cdot \overrightarrow{\nabla }c\mid }_{r_0}=\{\begin{array}{cc}\alpha \left(\theta \right)\hfill & \text{reaction-limited}.\hfill \\ {\phantom{\mid }\gamma \left(\theta \right)c\mid }_{r_0}\hfill & \text{diffusion-limited},\hfill \end{array}\phantom{\}}$$ (2)

where the catalytic activity of the particle is given by the surface flux, α(θ), or the surface flux per unit solute concentration, γ(θ). These quantities are positive or negative for, respectively, solute creation or destruction, and may vary with the polar angle θ on the particle (we assume azimuthal symmetry). We assume c|_∞ = k⁺/k⁻ is the bulk steady state far from the catalytic particle.

Solving Eq. (1) in three dimensions (see Appendix A for results in dimensions d = 1 and d = 2), we find the series:

$$c\left(r,\theta \right)=\frac{k^{+}}{k^{-}}+\sum _{\ell =0}^{\infty }{b}_{\ell }{k}_{\ell }\left(\frac{r}{\lambda }\right)P_{\ell }\left(\cos \theta \right),$$ (3)

where k_ℓ is the ℓ^th modified spherical Bessel function of the second kind [27, 28], P_ℓ is the ℓ^th Legendre polynomial, b_ℓ is a coefficient, and the decay length $\lambda =\sqrt{D_s∕k^{-}}$ is the typical distance that solute diffuses before being destroyed.

The perturbation of the solute concentration field due to the catalytic particle decays as

$$c\left(r\right)-\frac{k^{+}}{k^{-}}\sim \{\begin{array}{cc}\frac{1}{r}\hfill & r\ll \lambda \hfill \\ e^{-r∕\lambda }\hfill & r\gg \lambda \hfill \end{array}\phantom{\}}$$ (4)

On short length scales, the concentration field is similar to that of the inert medium [3], but on length scales longer than the decay length, the concentration field decays exponentially due to the activity of the medium.

We determine the coefficients, {b_ℓ}, from Eq. (2) by expanding the surface activity in Legendre polynomials [3]. In the reaction-limited case,

$$b_{\ell }=\frac{{\alpha }_{\ell }\left(2\ell +1\right)}{\sqrt{D_s{k}^{-}}\left(\ell k_{\ell -1}\left(\frac{r_0}{\lambda }\right)+\left(\ell +1\right)k_{\ell +1}\left(\frac{r_0}{\lambda }\right)\right)},$$ (5)

where α_ℓ is the ℓ^th coefficient in the expansion of α(θ). In the diffusion-limited case, b_ℓ is determined by solving the system of equations:

$$\begin{array}{cc}\hfill \frac{D_s{b}_{\ell }}{\lambda \left(2\ell +1\right)}& \left(\ell k_{\ell -1}\left(\frac{r_0}{\lambda }\right)+\left(\ell +1\right)k_{\ell +1}\left(\frac{r_0}{\lambda }\right)\right)=\hfill \\ \hfill & {\gamma }_{\ell }\frac{k^{+}}{k^{-}}+\sum _{n,m}{\gamma }_n{b}_m{k}_m\left(\frac{r_0}{\lambda }\right)c_{\mathit{nm}\ell },\hfill \end{array}$$ (6)

with $c_{\mathit{nm}\ell }={\int }_{-1}^1{P}_n\left(x\right)P_m\left(x\right)P_{\ell }\left(x\right)\mathit{dx}$ given by [29]. The infinite set of equations in Eq. (6) can be solved in closed form to any desired precision by setting b_ℓ = 0 for ℓ larger than a cuto ℓ* in the expansion of γ [30].

When the catalytic activity of the particle is asymmetric, it can self-propel. To determine the self-propulsion speed we calculate the slip velocity, v_s(θ) [3]. v_s is the difference between the particle velocity and the velocity of the ambient fluid at the surface of the particle [31]; this slip is responsible for net particle propulsion [3, 31, 32]. v_s arises from the tangential component of the concentration gradient at the particle surface [3, 31]:

$${\phantom{\mid }{\overrightarrow{v}}_s\left(\theta \right)=\mu \left(\theta \right){\overrightarrow{\nabla }}_{\Vert }c\mid }_{r_0},$$ (7)

where μ(θ) is the mobility coefficient [3, 31].

Using a version of the low Reynolds number reciprocal theorem [3, 32, 33], we find that the propulsion velocity, $\overrightarrow{v}$, is the slip velocity averaged over the surface of the particle (see Appendix B):

$$\overrightarrow{v}=-\frac{1}{4\pi r_0^2}\int {\overrightarrow{v}}_s\mathit{dS}.$$ (8)

Substituting for the slip velocity, ${\overrightarrow{v}}_s$, and integrating, we have:

$$\overrightarrow{v}=\frac{-\widehat{z}}{r_0}\sum _{\ell =1}^{\infty }{b}_{\ell }{k}_{\ell }\left(\frac{r_0}{\lambda }\right)\frac{\ell \left(\ell +1\right)}{2\ell +1}\left(\frac{{\mu }_{\ell -1}}{2\ell -1}-\frac{{\mu }_{\ell +1}}{2\ell +3}\right),$$ (9)

where {μ_ℓ} are the coefficients of the Legendre polynomials in the expansion of μ(θ).

B. Reaction-limited case

For the reaction-limited case, there are two scaling regimes for the propulsion speed, v:

$$v\sim \{\begin{array}{cc}\frac{\mu \alpha }{D_s}\hfill & \lambda \gg r_0,\hfill \\ \frac{\mu \alpha }{r_0\sqrt{D_s{k}^{-}}}\hfill & \lambda \ll r_0.\hfill \end{array}\phantom{\}}$$ (10)

The speed is proportional to the catalytic activity of the particle and the strength of the physical interaction between the particle and the solute species.

In the limit of slow bulk solute degradation, the activity of the medium is negligible over the length of the catalytic particle, which is small compared to solute decay length. Thus, v scales as in the inert medium, where self-propulsion is independent of particle size [3] because the concentration profile is scale-free on the scale of r₀.

When the catalytic particle is larger than the decay length, medium chemical activity qualitatively alters particle self-propulsion by perturbing the solute concentration. Thus, v decreases as particle size, r₀, and/or the bulk solute degradation rate, k⁻, increase. Unlike the size-dependence that arises with Michaelis-Menten surface kinetics [34], the r₀-dependence here arises from the importance of the activity of the underlying medium over length scales > λ. Eq. (10) demonstrates that the chemical properties of the medium, in addition to its physical properties such as viscosity, η ∝ 1/D_s, control self-propulsion of catalytic particles.

C. Diffusion-limited case

For diffusion-limited systems, self-propulsion depends on the chemical properties of the medium for all particle sizes. For the simplest case with self-propulsion, we consider the minimal asymmetric model with γ(θ) = γ₀ + γ₁P₁(cos θ).

To simply describe the system, we reduce the parameters by nondimensionalizing the reaction-diffusion equation by rescaling lengths by $\lambda =\sqrt{D_s∕k^{-}}$ and concentrations by c₀ = k⁺/k⁻:

$${\nabla }^{2}c-c+1=0.$$ (11)

Thus, the boundary condition, Eq. (2b), is written as:

$${\phantom{\mid }-\widehat{r}\cdot \overrightarrow{\nabla }c\mid }_{r=R}={\phantom{\mid }\left(g_0+g_1\cos \theta \right)c\mid }_{r=R}$$ (12)

where R = r₀/λ is the dimensionless particle size, and $g_0={\gamma }_0∕\sqrt{D_s{k}^{-}}$ and $g_1={\gamma }_1∕\sqrt{D_s{k}^{-}}$ are the dimensionless catalysis rates.

The concentration is now written as:

$$c\left(r,\theta \right)=\left(1+\sum _{\ell =0}^{\infty }{\tilde{b}}_{\ell }{k}_{\ell }\left(R\right)\right)c_0$$ (13)

where ${\tilde{b}}_{\ell }=b_{\ell }∕c_0$. Consequently, the self-propulsion speed scales as:

$$v\sim \frac{\mu }{r_0}{c}_0{\tilde{b}}_1{k}_1\left(R\right)$$ (14)

where the coefficient ${\tilde{b}}_1$ is found through a systematic approximate solution to the system of equations, Eq. (6) (see Appendix C).

For sufficiently small g₀ and g₁, defined approximately as $g_0+\frac{2}{3}\mid g_1\mid \ll \frac{1}{R}+1$, the self-propulsion speed scales as (see Appendix C):

$$v\sim \{\begin{array}{cc}\frac{\mu {\gamma }_1{k}^{+}}{D_s{k}^{-}}\hfill & R\ll \min (\frac{1}{\mid g_0\mid },\frac{1}{\mid g_1\mid },1),\hfill \\ \frac{\mu {\gamma }_1{k}^{+}}{r_0\sqrt{D_s}{\left(k^{-}\right)}^{3∕2}}\hfill & R\gg 1.\hfill \end{array}\phantom{\}}$$ (15)

v is insensitive to γ₀ at leading order, but it varies linearly in γ₀ for small γ₀ and as $1∕\mid {\gamma }_0\mid$ for very negative γ₀ (inset to Fig. 1a). Thus, for slow surface catalysis, v scales as in the reaction-limited case, Eq. (10), but multiplied by the solute concentration, c₀ = k⁺/k⁻, sustained by the medium.

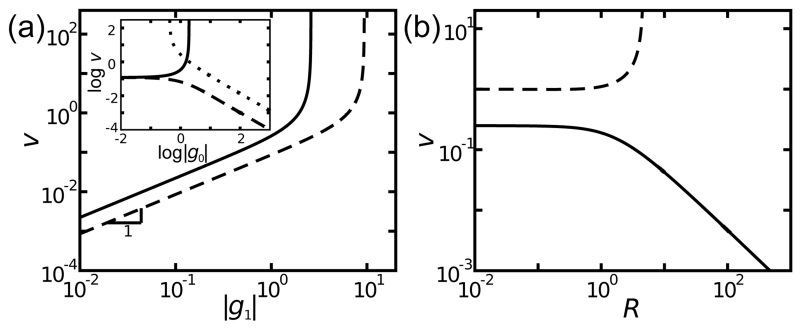
FIG. 1. Scaling of v for diffusion-limited cases.

a) v (in units of μc₀/r₀) grows linearly in |g₁| until diverging. Solid and dashed lines show v with g₀ = ±|g₀|, respectively. Inset: v for g₀ > 0 with small |g₁| (solid), g₀ < 0 with small |g₁| (dashed), and g₀ < 0 with large |g₁| (dotted). v grows linearly with |g₀| for small |g₀| if g₁ is sufficiently small, but decays as 1/|g₀| for sufficiently negative g₀ (dashed) or diverges for large |g₀| (solid). For large |g₁|, steady-state v exists only for sufficiently negative g₀ (dotted). b) v is insensitive to R at small R, but decays at large R as 1/R if g₀ and |g₁| are sufficiently small (solid) and diverges otherwise (dashed).

Rapid solute production by the catalytic particle can overwhelm the destruction of solute by the medium. In that case, the model assumptions are not compatible with a nonequilibrium steady-state. As in Fig. 1a, v diverges for large g₀ and |g₁|. Similarly, for large g₀ and |g₁|, v diverges for large particles since the total surface catalysis overwhelms background activity (Fig. 1b). Mathematically, these divergences arise from the zeros of the denominator of the expression for the coefficient ${\tilde{b}}_1$ (see Eq. (C1)). In a real autocatalytic system (e.g., actin filament networks [35]), surface catalysis saturates at high concentration, and thus, the system should transition to a steady-state with the boundary condition in Eq. (2a) and velocity in Eq. (10).

III. INTERACTIONS

A. Screening of interactions

Catalytic particles are capable of self-organization through their interactions with the concentration fields generated by other catalytic particles [10-13, 36]. In an inert medium, these interactions are long-ranged, decaying as 1/r (Eq. (4a)) [12, 13]. In a chemically active medium, however, the solute distribution decays exponentially (Eq. (4b)). A similar screening length arises in the limit of many closely-packed catalytic particles in the diffusion-limited (“unsaturated”) regime, which is discussed in [13]. Thus, as with electrostatic interactions in an ionic solution, diffusiophoretic interactions in an active medium are exponentially screened.

B. Simulation model

To understand interactions in a biochemically active medium, we developed a Brownian dynamics simulation model in which catalytic particles chemically and physically interact with rapidly diffusing solute molecules. We consider catalytic particles of radius r₀ that repel each other by excluded volume interactions in a periodic system of size L. These particles act as potential wells for diffusing solute molecules, binding solute within a distance r₀ with energy ε. While bound, solute molecules are degraded by the catalytic particle at rate $k_c^{-}$. Solute particles diffuse with coefficient D_s = 1000D_c, are degraded by the medium at rate k⁻ when not bound to a catalytic particle, and are produced by the medium at rate k⁺. The coupling of physical and chemical interactions models a collection of enzymes, each of which must bind its substrate before catalyzing a reaction. Additional model details are provided in Appendix D. Although some details of the simulation differ from the theory, the simulation can be described by the theory with an appropriate choice of surface activity, as described in Appendix E.

The interactions between two diffusiophoretic particles depend on the whether the particles locally deplete or enhance the solute concentration and whether they attract or repel solute [12]. In the simulation, the effective surface activity, α, is proportional to the ambient concentration k⁺/k⁻ and the composite rate, $k^{-}-e^{\beta ϵ}{k}_c^{-}$, comparing solute degradation by the medium to solute degradation and sequestration (binding) by the catalytic particle (Eqs. (E9) and (E10)). Thus, enzyme-like machines in a biochemically active medium repel each other when $k^{-}<k_c^{-}{e}^{\beta ϵ}$, attract when $k^{-}>k_c^{-}{e}^{\beta ϵ}$, and do not interact when $k^{-}=k_c^{-}{e}^{\beta ϵ}$.

A catalytic particle locally depletes solute by binding it with energy ε and degrading it at rate $k_c^{-}$. The concentration of solute bound to the catalytic particle is $e^{\beta ϵ}$ times larger than the local medium solute concentration; this enhances the rate of solute depletion by the particle by $e^{\beta ϵ}$. Thus, even if $k_c^{-}<k^{-}$, solute can be depleted from the medium if it only rarely unbinds from the catalytic particle (large ε). However, if catalytic particles degrade solute more slowly than the medium and the binding time is short (small ε), the particle behaves as solute source. This demonstrates that interactions, and thus self-organization, may be altered through manipulation of either the active medium or the catalytic particle properties.

C. Simulation results and theoretical analysis

To quantify interactions, we construct an effective equilibrium theory incorporating both excluded volume and concentration-gradient-mediated interactions. For simplicity, we consider the simplest case with symmetric particles, which do not independently self-propel (i.e., only considering the ℓ = 0 terms of the Legendre polynomial expansions of α(θ) and μ(θ)). However, the analysis can be generalized to specific cases of asymmetric, self-propulsive particles as well (by considering the ℓ > 0 terms in the expansions).

Excluded volume directly induces repulsive forces on length scales r < 2r₀, which leads to an effective entropic repulsion over longer length scales. Catalytic particles also interact through their concentration fields. Thus, the effective interaction potential between particles is:

$$U\left(r\right)=\{\begin{array}{cc}\infty \hfill & r<2r_0,\hfill \\ -ϵ\mathit{wc}\left(r\right)\hfill & r>2r_0,\hfill \end{array}\phantom{\}}$$ (16)

where c(r) is the single-particle concentration profile (e.g., Eq. (E1) for d = 3 or Eq. (E11) for d = 1) and w is the volume of the solute-binding region of the machine. Since the solute concentration is continuously in steady state with respect to the catalytic particle positions, it acts as a static potential. The coefficient, ε, is the binding energy.

For $\sqrt{D_s∕D_c}\gg \lambda ∕r_0$, this approach is justified by the separation of timescales between particle motions and concentration profile perturbations. In particular, the effective equilibrium approximation used to estimate interactions between catalytic particles relies on the separation of the characteristic timescale, τ_c, for catalytic particle motion from the lifetime, τ_s, of perturbations to the solute concentration profile.

The timescale for catalytic particle motion is given by the diffusion coefficient as: ${\tau }_c=r_0^2∕D_c$. Since the particles are symmetric, they do not self-propel, so there is no need to consider an effective temperature description [37] based on the intrinsic velocity of the catalytic particles.

The lifetime for perturbations to the solute concentration profile can be calculated by considering linear perturbations to the reaction-diffusion equation (Eq. (1)):

$${\partial }_t\delta c=D_s{\nabla }^2\delta c-k^{-}\delta c.$$ (17)

Writing $\delta c=\sum \delta \tilde{c}\left(q,\omega \right)e^{i\left(\mathit{qr}-\omega t\right)}$, we find $i\omega =q^2{D}_s+k^{-}$, implying ${\tau }_s\left(q\right)={(q^2{D}_s+k^{-})}^{-1}$.

For the timescales to be comparable, we must have $q^2{D}_s+k^{-}\approx D_c∕r_0^2$. This is only satisfied for real q if $r_0\sqrt{D_s∕D_c}<\lambda$; otherwise ${\tau }_c>{\tau }_s\left(q\right)$ for all real q, as desired for the equilibrium approximation. Since D_s ≫ D_c by assumption, τ_c ≈ τ_s(q) requires either the catalytic particle to be very small or the bulk solute decay rate to be very slow. Thus, the assumption of separation of timescales is valid if $\sqrt{D_s∕D_c}\gg \lambda ∕r_0$. This is satisfied in our simulations, where $\sqrt{D_s∕D_c}\approx 32$ and λ/r₀ ≈ 2.2 (moreover, the slowest τ_s(q) is τ_s(q = 0) = 20, which is much shorter than τ_c = 4000).

As a further consistency check, we consider the timescale for particle motion due to the effects of the concentration fields generated by other particles. This time scale is ${\tau }_c^v=r_0∕\mid v\mid$, where the speed, |v|, is calculated as the magnitude of the effective force, $F=wϵ\mid \nabla c\mid$, divided by the particle drag coefficient, k_BT/D_c. Since $\mid \nabla c\mid \lesssim \mid \alpha \mid ∕D_s$ and w = 2r₀ in one dimension, we have ${\tau }_c^v\approx \left(D_s∕D_c\right)\left(k_{B}T∕2ϵ\mid \alpha \mid \right)$.

From Eq. (E12), which gives the effective surface catalysis rate in the simulation, we note that |α| < k⁺ max(r₀, λ). Since D_s/D_c ≫ 1, we also have ${\tau }_c^v\gg {\tau }_s$ unless ε, k⁺, r₀ or λ is very large. For the simulations considered, we have ${\tau }_c^v>231$ compared to τ_s(q) ≤ 20.

To directly test the equilibrium approximation, we compare the theory with the simulation in the case where the two machines are pushed together by an external force, F . In the theory, the inter-particle force-distance relation is given by the statistical-mechanical relation:

$$\langle r\rangle =-\frac{\partial \ln \mathcal{Ƶ}}{\partial \left(\beta F\right)}=\frac{{\int }_{0\le r\le L∕2}{\mathit{re}}^{-\beta \left(\mathit{Fr}+U\left(\overrightarrow{r}\right)\right)}{d}^{d}r}{{\int }_{0\le r\le L∕2}{e}^{-\beta \left(\mathit{Fr}+U\left(\overrightarrow{r}\right)\right)}{d}^{d}r},$$ (18)

which can be expressed exactly for the inert medium (see Appendix F).

Distance fluctuations, $\langle \delta r^2\rangle =\langle r^2\rangle -{\langle r\rangle }^2$, can be derived in a similar manner (Eq. (F4)). As shown for the one-dimensional examples in Fig. 2, the theory (lines) agrees with the simulation (circles) provided that the concentration near each particle is large enough that the continuum approximation is valid and small number fluctuations are unimportant. This requires $c_{\min }\approx \min \left(\frac{k^{+}}{k_c^{-}}{e}^{-\beta ϵ},\frac{k^{+}}{k^{-}}\right)>1∕{\lambda }^d$, similar to Debye-Huckel theory.

FIG. 2. Force-distance relation and distance fluctuations from theory and simulation.

a) Without chemical activity, particles pushed together with force F (units of 2k_BT/r₀) entropically repel (solid line). 〈r〉 as a function of F is depressed for attractions in both the theory (dashed line) and simulation (solid circles). 〈r〉 is larger for repulsions in the theory (dash-dotted line) and simulation (open circles). Dotted line shows 〈r〉 = 2r₀ and L = 30. b) The corresponding distance fluctuations.

Using the equilibrium theory, we studied how changes in the underlying medium affect the mean distance, 〈r〉, and fluctuations, 〈δr²〉, between interacting catalytic particles in d = 1 (Fig. 3). 〈r〉 varies non-monotonically with k⁻ (Fig. 3a, solid line). For slow bulk degradation ($k^{-}<k_c^{-}{e}^{\beta ϵ}$), particles are repulsive, so 〈r〉 is larger than the zero-activity mean distance, L/4 + r₀ (dotted line). With fast bulk degradation ($k^{-}>k_c^{-}{e}^{\beta ϵ}$), particles are attractive, so 〈r〉 decreases to 2r₀. For very fast k⁻, the solute concentration is low, so particle interactions vanish and 〈r〉 approaches its non-interacting value.

FIG. 3. Medium activity controls mean distance and fluctuations.

a) 〈r〉 varies non-monotonically with k⁻ (solid line). 〈r〉 ≈ L/2 for strong repulsions and 〈r〉 ≈ 2r₀ for strong attractions. For weak interactions, i.e., $k^{-}\approx k_c^{-}{e}^{\beta ϵ}$ (vertical line) or large k⁻, 〈r〉 → L/4 + 2r₀ (dotted). b) $\sqrt{\langle \delta r^2\rangle }$ is small for $k^{-}<k_c^{-}{e}^{\beta ϵ}$ and $k^{-}\gtrsim k_c^{-}{e}^{\beta ϵ}$, but large for $k^{-}\approx k_c^{-}{e}^{\beta ϵ}$ and large k⁻. c) As k⁺ increases, 〈r〉 decreases/increases toward maximum compression/extension for attractions/repulsions (solid/dashed). d) For large k⁺, $\sqrt{\langle \delta r^2\rangle }$ decreases as 1/k⁺ for attractions (solid) and $1∕\sqrt{k^{+}}$ for repulsions (dashed). L = 50 in all panels.

Inter-particle distance fluctuations also vary non-monotonically with k⁻ (Fig. 3b, solid line). For k⁻ such that the attractions or repulsions are strong, fluctuations are small, since the particles are tightly held in their equilibrium positions. However, for $k^{-}\approx k_c^{-}{e}^{\beta ϵ}$, the interactions are weak, so 〈δr²〉 approaches the inert limit, 〈δr²〉 = (L – 4r₀)²/48. The particles also interact weakly and exhibit large distance fluctuations for large k⁻, when the ambient concentration is low.

As the bulk production rate, k⁺, increases, interaction strength grows linearly, and particles transition from weakly to strongly interacting. However, changes to k⁺ cannot change the sign of interactions. Thus, 〈r〉 is nearly the inert particle limit for small k⁺, but for large k⁺, approaches maximum compression or separation for attractive or repulsive interactions, respectively (Fig. 3c).

The increase in interaction strength with increasing k⁺ manifests as a power law decay in fluctuations (Fig. 3d). For large $k^{+},\sqrt{\langle \delta r^2\rangle }\sim 1∕k^{+}$ for attractive interactions and $\sqrt{\langle \delta r^2\rangle }\sim 1∕\sqrt{k^{+}}$ for repulsive interactions. The power laws differ because attractive interactions are dominated by the shape of the solute concentration field at short length scales, whereas repulsive interactions are dominated by its shape at long length scales.

D. Effective force

To determine whether diffusiophoretic interactions are relevant in biological systems, we estimate the force arising from the d = 3 solute concentration profile (again assuming separation of timescales). The effective force due to diffusiophoretic interactions can be estimated by considering the solute concentration profile generated by the combined activity of the catalytic particles and the underlying medium.

In d = 3, the concentration profile surrounding a catalytic particle with surface activity α (in the reaction-limited system) or γ (in the diffusion-limited system) is given by Eq. (E1). In the reaction-limited case (see Appendix G for the diffusion-limited case), the resulting radial concentration gradient is:

$${\partial }_{r}c=-\frac{\alpha k_1\left(r∕\lambda \right)}{{\lambda }^2{k}^{-}{k}_1\left(r_0∕\lambda \right)}.$$ (19)

We estimate the characteristic effective force, F*, due to concentration-gradient mediated interactions by εw∂_rc at one screening length from the surface of the catalytic particle (r = r₀ + λ):

$$F^{\ast }={\phantom{\mid }ϵw{\partial }_{r}c\mid }_{r=r_0+\lambda }.$$ (20)

Estimating the volume of interaction between particle and solute as $w\approx r_0^3$ (as in the simulation model), we have:

$$F^{\ast }=-\frac{ϵ\alpha r_0^5\left(r_0+2\lambda \right)}{e{\lambda }^2{k}^{-}{(r_0+\lambda )}^3}.$$ (21)

Thus, we find that F* scales as:

$$F^{\ast }\sim \{\begin{array}{cc}-\frac{ϵ\alpha r_0^5{k}^{-}}{D_s^2}\hfill & r_0\ll \lambda \hfill \\ -\frac{ϵ\alpha r_0^2}{D_s}\hfill & r_0\gg \lambda \hfill \end{array}\phantom{\}}$$ (22)

Assuming ε ≈ few k_BT , D_s ≈ 1 μm²/s, k⁻ = 0.1 s⁻¹, and α = 0.01 nm⁻² s⁻¹ (i.e., 1 enzyme with catalysis rate 1 s⁻¹ per 100 nm²), F * ≈ 1 pN for μm-sized particles. We therefore conclude that diffusiophoretic interactions can be important in biological systems.

IV. APPLICATION TO BACTERIAL PLASMID PARTITIONING

Experiments and models suggest that chromosome segregation, plasmid partitioning, and positioning of organelle-like structures by the bacterial ParAB system are phoretically driven by a ParA protein gradient [21, 22, 24, 38-43]. In plasmid partitioning, the protein ParB binds to parS-sites of plasmid DNA while ParA binds the nucleoid. ParA molecules diffuse along the nucleoid until dissociating into the cytoplasm. The ParB-parS complex binds ParA, stimulating faster ParA dissociation from the nucleoid. This system spaces plasmids equally throughout the rod-shaped bacterium [44].

We interpret this as phoretic interactions between plasmids. Since ParB sequesters and dissociates ParA from the surrounding nucleoid, it locally depletes ParA, as observed in vivo [45] and in vitro [24, 40, 41]. This induces effective repulsions between ParB-bound plasmids, which move toward high ParA concentration. ParA polymerization and depolymerization [46], may quantitatively, but not qualitatively, alter this mechanism.

The bacterium is approximately a one-dimensional system. For such a system, the effective force, F* = εw∂_xc, may be derived from the one-dimensional concentration profile, approximately given by L → ∞ limit of Eq. (E11). Thus, we estimate the effective force with w = r₀, as:

$$F^{\ast }=ϵw{\partial }_{x}c=-\text{sgn}\left(x\right)\frac{ϵ\alpha r_0}{{\mathit{eD}}_s}.$$ (23)

For the ParAB plasmid partitioning system, where the catalytic particle binds and degrades solute as described for the simulation, the effective surface catalysis rate is approximately given by the L → ∞ limit of Eq. (E12):

$$\alpha =\frac{\left(k^{+}∕k^{-}\right)\left(k^{-}-e^{\beta ϵ}{k}_c^{-}\right){\lambda }_c{e}^{r_0∕{\lambda }_c}\sinh \left(r_0∕{\lambda }_c\right)}{1+\sqrt{k_c^{-}∕k^{-}}{e}^{\beta ϵ}{e}^{r_0∕{\lambda }_c}\sinh \left(r_0∕{\lambda }_c\right)}.$$ (24)

To estimate the interaction range and effective force, we use measurements from in vitro and in vivo experiments. We assume D_s = 0.85 μm²/s and k⁻ = 0.032 s⁻¹, which were measured in vitro [41]. To estimate the association rate, which is the effective production rate, we estimate 2400 ParA molecules per nucleoid as measured in [43] and estimate that the nucleoid is 3 μm in length. We set this (d = 1) concentration equal to k⁺/k⁻ in order to arrive at k⁺ = 25 s⁻¹μm⁻¹, which is consistent with the estimate in [43] and also the in vitro experiments in [38, 40, 41]. We estimate that ε ≈ few k_BT , consistent with the dynamics of ParA-ParB-parS complexes observed in in vitro experiments [40, 41, 47]. We estimate k_c⁻ ≈ 10k⁻ which is approximately the rate at which ParB-stimulated hydrolysis of ParA-ATP occurs in vitro [47, 48]; however, we note that using a higher rate, k_c⁻, as in [43] increases α by an $\mathcal{O}\left(1\right)$ factor. Finally, we estimate r₀ ≈ 0.1 μm based on in vivo fluorescence images such as those in [43].

We thus estimate an interaction range of λ ≈ 5 μm and, by Eq. (23), we estimate an effective force of order 10 fN. λ is long enough to facilitate plasmid interactions. F * is comparable to the ≈ 10 fN viscous drag that plasmids experience in vivo [49], and sufficient to self-organize plasmids against thermal fluctuations.

V. CONCLUSION

Our model demonstrates a novel mechanism for controlling self-propulsion and self-organization. The chemical activity of the underlying medium affects these behaviors by altering the steady-state solute concentration field. Tuning the background activity can change both the strength and the sign of interparticle interactions, and define length scales of order λ, which may be much larger than the size of the solute molecules or the enzymatic machines. For the ParAB bacterial plasmid partitioning system, our estimates suggest that the relevant length scale, λ, is in the range of microns, and forces on protein-coated plasmids are in the ten femtonewton range. In general, the effective force generated by catalytic machines in other in vivo scenarios could be as large as a few piconewtons.

Our results suggest a number of general comments. First, we anticipate that catalytic particle properties (transport, interactions, and self-organization) within cells might be controlled by altering the composition of macromolecular complexes or post-translational protein modifications (PTPMs, e.g., phosphorylation). Second, since the behavior of the catalytic machines is dependent on their environment and its activity as well, we expect transport and interaction effects from changes in cytoplasmic properties. Such “medium” properties might be manipulated by (over)expressing enzymes that degrade reactant “solute” molecules. In terms of intracellular regulation, cells could change bulk concentrations and kinetics of small biomolecules such as NTPs or proteins with specific NTPs and PTPMs to modulate organization of catalytic particles or organelles. Finally, we note that at supracellular scales, chemotactic cells such as bacteria or immune cells may utilize similar principles to those discussed in this paper to mediate swarming or dispersive interactions.

Appendix A: Reaction-diffusion equation in d = 1 and d = 2

In d = 1, the solution to Eq. (1)) is:

$$c_{\pm }\left(x\right)=\frac{k^{+}}{k^{-}}+b_{\pm }{e}^{-\left(\mid x\mid -r_0\right)∕\lambda },$$ (A1)

where + and − subscripts, respectively, denote the solutions for x > r₀ and x < −r₀.

In d = 2, we have:

$$c\left(r,\theta \right)=\sum _{\ell =0}^{\infty }{K}_{\ell }\left(r∕\lambda \right)\left(b_{\ell }^c\cos \left(\ell \theta \right)+b_{\ell }^s\sin \left(\ell \theta \right)\right),$$ (A2)

where K_ℓ is a modified Bessel function of the second kind.

Appendix B: Derivation of the self-propulsion velocity

As described in [32], the reciprocal theorem for low Reynolds number hydrodynamics [33] may be used to solve for the velocity, $\overrightarrow{v}$, of self-propelled particle in terms of the drag force, $\overrightarrow{F}$ acting against motion and the fluid velocity, $\overrightarrow{u}$, at the surface of the object:

$$\overrightarrow{F}\cdot \overrightarrow{v}=-\int \widehat{n}\cdot \sigma \cdot \overrightarrow{u}\mathit{dS},$$ (B1)

where σ is the stress on the particle surface due to motion against the fluid and the integration is performed over the surface of the particle.

In the model, the surface velocity, $\overrightarrow{u}$, is the slip velocity, ${\overrightarrow{v}}_s$, arising from the tangential component of the concentration gradient at the particle surface [3]. Thus, for a spherical particle with $\overrightarrow{F}=6\pi \eta r_0\overrightarrow{v}$ and $\widehat{n}\cdot \sigma =-\frac{3\eta }{2r_0}\overrightarrow{v}$, we find that the propulsion velocity is the slip velocity averaged over the surface of the particle:

$$\overrightarrow{v}=-\frac{1}{4\pi r_0^2}\int {\overrightarrow{v}}_s\mathit{dS}.$$ (B2)

Substituting for the slip velocity, ${\overrightarrow{v}}_s$, we have:

$$\overrightarrow{v}=\frac{\widehat{z}}{4\pi r_0^2}{\int }_0^{2\pi }d\varphi {\int }_0^{\pi }{r}_0^2{\sin }^2\theta d\theta \sum _{\ell =0}^{\infty }{\mu }_{\ell }{P}_{\ell }\left(\cos \theta \right){\phantom{\mid }\frac{1}{r_0}{\partial }_{\theta }c\mid }_{r=r_0},$$ (B3)

where we have expanded μ(θ) in Legendre polynomials. Integrating this expression leads to Eq. (9).

Appendix C: Scaling of the self-propulsion velocity in the diffusion-limited system

In order to approximately solve Eq. (6) in a systematic manner, we assume that b_ℓ≥2 = 0. Thus, the coefficient ${\tilde{b}}_1$ is approximately:

$${\tilde{b}}_1\approx \frac{3e^R{R}^3\left(3+R\left(3-g_0\right)\right)g_1}{18+9R\left(4-3g_0\right)+R^2\left(27-36g_0+9g_0^2-4g_1^2\right)+R^3\left(9-18g_0+9g_0^2-4g_1^2\right)},$$ (C1)

where R, g₀, and g₁ are reduced variables as described in Section II C.

We first consider the limit of reduced catalysis rates, g₀ and g₁, that are sufficiently small so that the catalysis of the particle does not overwhelm the catalysis of the medium. Thus, we only have physical solutions when g₀ is sufficiently small or negative and |g₁| is sufficiently small. The maximum values of these parameters is given by the smallest real root of the denominator in Eq. (C1) (i.e., the values of g₀ and g₁ for which ${\tilde{b}}_1$ diverges).

There is a maximum value for g₀; on the other hand, if g₀ is very negative, the catalytic particle destroys solute very quickly, which leads to a valid steady-state with low solute concentration. If g₀ were too large, concentration-dependent solute production by the catalytic particle could overcome the concentration-dependent destruction of solute in the medium.

For g₁, there is an upper limit to its absolute value; since P₁(cos θ) = cos θ is positive for one half of the particle surface, but negative for the other half, g₁ is related to both destruction and production of solute, regardless of its sign. Moreover, the expression for ${\tilde{b}}_1$ is manifestly odd in g₁. Since the total rates of solute catalysis at the particle surface by the ℓ = 1 term depend on the local solute concentration, if |g₁| is too large, production of solute on one side of the catalytic particle can overwhelm solute destruction on the other side of the particle and the entire medium. In that case, there is no physically-meaningful steady-state solution to the reaction-diffusion equation, and the solute concentration grows without bound. We note that in a real system, this unphysical behavior would be cut off by physical effects not considered in this formulation of the boundary condition, such as saturation of the activity at the particle surface.

The denominator in Eq. (C1) is zero for

$$g_0=\frac{9+12R+6R^2\pm \sqrt{9+16g_1^2{R}^2\left(1+2R+R^2\right)}}{6R\left(1+R\right)}$$ (C2)

and

$$g_1=\pm \frac{3\sqrt{2+4R+3R^2+R^3-3{\mathit{Rg}}_0-4R^2{g}_0-2R^3{g}_0+R^2{g}_0^2+R^3{g}_0^2}}{2R\sqrt{1+R}}.$$ (C3)

As discussed above, g₀ must be small enough or sufficiently negative to overcome the solute production due to g₁, so g₀ must be less than the “–” expression in Eq. (C2). In contrast, since |g₁| must be small, we require that g₁ lie between the “+” and “–” solutions of Eq. (C3).

To simplify these expressions, we first combine the small and large R limits of Eq. (C2) to obtain an approximate threshold. This yields $g_0+\frac{2}{3}\mid g_1\mid <\frac{1}{R}+1$, which requires g₀ and |g₁| strictly less than the actual thresholds in Eqs. (C2)-(C3).

Since $\mid {\tilde{b}}_1\mid \to \infty$ is unphysical (and moreover, Eq. (C1) is approximate, with the approximation worsening near the divergence in ${\tilde{b}}_1$), we assume that g₀ and g₁ are small enough that we are far from these threshold values.

With these assumptions, for R ≪ 1, we find:

$${\tilde{b}}_1\approx g_1\left(\frac{1}{2}{R}^2+\frac{7}{12}{g}_0{R}^4+\frac{1}{72}\left(45g_0^2-24g_0+8g_1^2\right)R^5\right),$$ (C4)

which is the exact expression for ${\tilde{b}}_1$ to $\mathcal{O}\left(R^4\right)$. (The exact expression for ${\tilde{b}}_1$ to $\mathcal{O}\left(R^6\right)$ may be found by calculating ${\tilde{b}}_1$ under the assumption b₃ = 0, etc.)

Thus, for $R\ll 1,{\tilde{b}}_1\sim g_1{R}^3$ provided that $R<\frac{6}{7\mid g_0\mid }\approx \frac{1}{\mid g_0\mid }$ (so that the $\mathcal{O}\left(R^4\right)$ does not dominate) and $R<\frac{3}{g_1\sqrt{2}}\approx \frac{1}{\mid g_1\mid }$ (so that $\mathcal{O}\left(R^5\right)$ does not dominate if g₀ ≈ 0).

For R ≫ 1, we have:

$${\tilde{b}}_1\approx \frac{3e^{R}R\left(3-g_0\right)g_1}{9-18g_0+9g_0^2-4g_1^2},$$ (C5)

which scales as ${\tilde{b}}_1\sim g_1{\mathit{Re}}^R$ for small g₀ and |g₁|.

By combining these scaling expressions with the scaling of k₁(R) with R, we arrive at Eq. (15).

Finally, the scaling with g₀ can be extracted by noting that near $g_0=0,\frac{\partial {\tilde{b}}_1}{\partial g_0}\approx \text{constant}>0$, whereas for $g_0\to -\infty ,{\tilde{b}}_1\sim 1∕\mid {\alpha }_0\mid$.

Appendix D: Simulation details

The catalytic particles of radius r₀ effiectively maintain excluded volume interactions through a short-ranged harmonic repulsion, which is given by:

$$U_R\left(r\right)=\frac{K}{2}{(r-2r_0)}^2,$$ (D1)

for r < 2r₀, where K = 500k_BT.

Catalytic particles bind solute particles through a Lennard-Jones-like potential, which is truncated at r = r_c so that energy and force are zero at the edge of the potential well:

$$U\left(r\right)=\{\begin{array}{cc}-ϵ+\frac{ϵ}{{\sigma }^{12}-{\sigma }^{14}}\left({\left(\frac{\sigma }{r_c}\right)}^{12}-{\left(\frac{\sigma }{r_c}\right)}^{14}+a\left(\frac{14{\sigma }^{14}}{r_c^{15}}-\frac{12{\sigma }^{12}}{r_c^{13}}\right)\right)\hfill & r<a,\hfill \\ \frac{ϵ}{{\sigma }^{12}-{\sigma }^{14}}\left({\left(\frac{\sigma }{r}\right)}^{14}-{\left(\frac{\sigma }{r}\right)}^{12}-{\left(\frac{\sigma }{r_c}\right)}^{14}+{\left(\frac{\sigma }{r_c}\right)}^{12}+r\left(\frac{14{\sigma }^{14}}{r_c^{15}}-\frac{12{\sigma }^{12}}{r_c^{13}}\right)\right)\hfill & a<r<r_c,\hfill \\ 0\hfill & \text{else},\hfill \end{array}\phantom{\}}$$ (D2)

where $\sigma =a\sqrt{6∕7}$ fixes the minimum to a. The minimum energy is approximately −ε. We set a = 1 and r_c = r₀ = 2 in our simulations.

All particles in the simulation are also subject to Brownian noise, F (t), which is described by:

$$\langle \overrightarrow{F}\left(t\right)\rangle =0$$ (D3)

$$\langle \overrightarrow{F}\left(t\right)\cdot \overrightarrow{F}\left(t^{\prime }\right)\rangle =2{\mathit{dk}}_{B}T\zeta \delta \left(t-t^{\prime }\right),$$ (D4)

where ζ is the particle drag.

The equations of motion are given by [50]:

$$\zeta \dot{\overrightarrow{r}}=-\overrightarrow{\nabla }\left(U_R+U\right)+\overrightarrow{F}\left(t\right),$$ (D5)

which we integrate using an Euler algorithm.

Appendix E: Mapping theory onto simulation

In the theoretical model described above, symmetric catalytic particles produce the following steady-state concentration fields:

$$c\left(r\right)=\{\begin{array}{cc}\frac{k^{+}}{k^{-}}+\frac{{\alpha }_0{k}_0\left(\frac{r}{\lambda }\right)}{\sqrt{D_s{k}^{-}}{k}_1\left(\frac{r_0}{\lambda }\right)}\hfill & \begin{array}{c}\text{reaction-}\hfill \\ \text{limited},\hfill \end{array}\hfill \\ \frac{k^{+}}{k^{-}}\left(1+\frac{{\gamma }_0{k}_0\left(\frac{r}{\lambda }\right)}{\left(\sqrt{D_s{k}^{-}}\right(1+\frac{\lambda }{r_0})-{\gamma }_0)k_0\left(\frac{r_0}{\lambda }\right)}\right)\hfill & \begin{array}{c}\text{diffusion-}\hfill \\ \text{limited}.\hfill \end{array}\hfill \end{array}\phantom{\}}$$ (E1)

The steady-state solute concentration distribution in the simulation corresponds to the following set of reaction-diffusion equations:

$$D_s{\nabla }^{2}c-k^{-}c+k^{+}=0r>r_0,$$ (E2)

$$D_s{\nabla }^{2}c-k_c^{-}c+k^{+}=0r<r_0.$$ (E3)

The matching conditions at the boundary, r = r₀, are approximately given by:

$${\phantom{\mid }c\mid }_{r\to r_0^{-}}={\phantom{\mid }{e}^{\beta ϵ}c\mid }_{r\to r_0^{+}},$$ (E4)

$${\phantom{\mid }{\partial }_{r}c\mid }_{r\to r_0^{-}}={\phantom{\mid }{\partial }_{r}c\mid }_{r\to r_0^{+}}.$$ (E5)

Note that this is an approximation because the potential given in Eq. (D2) is smooth rather than infinitely sharp at r = r₀.

In a system of infinite size in d = 3, the solution to these equations is:

$$c\left(r\right)=\{\begin{array}{cc}\frac{k^{+}}{k_c^{-}}+B_0{i}_0\left(\frac{r}{{\lambda }_c}\right)\hfill & r<r_0,\hfill \\ \frac{k^{+}}{k^{-}}+b_0{k}_0\left(\frac{r}{{\lambda }_c}\right)\hfill & r>r_0,\hfill \end{array}\phantom{\}}$$ (E6)

where ${\lambda }_c=\sqrt{D_s∕k_c^{-}}$ and i₀ is the 0^th modified spherical Bessel function of the first kind ($i_{\ell }\left(x\right)=\sqrt{\frac{\pi }{2x}}{I}_{\ell +1∕2}\left(x\right)\left[27\right]$), and B₀ and b₀ are constants determined from the matching conditions. These constants are:

$$B_0=\frac{k^{+}(e^{\beta ϵ}{k}_c^{-}-k^{-})r_0\left(r_0+\lambda \right)\mathrm{sech}\left(\frac{r_0}{{\lambda }_c}\right)}{k^{-}{k}_c^{-}\left(r_0\lambda e^{\beta ϵ}+{\lambda }_c\left(r_0+\lambda \left(1-e^{\beta ϵ}\right)\right)\tanh \left(\frac{r_0}{{\lambda }_c}\right)\right)},$$ (E7)

$$b_0=\frac{k^{+}(k^{-}-e^{\beta ϵ}{k}_c^{-})r_0{e}^{r_0∕\lambda }\left(r_0-{\lambda }_c\tanh \left(\frac{r_0}{{\lambda }_c}\right)\right)}{k^{-}{k}_c^{-}\left(e^{\beta ϵ}{r}_0\lambda +{\lambda }_c\left(r_0+\lambda \left(1-e^{\beta ϵ}\right)\right)\tanh \left(\frac{r_0}{{\lambda }_c}\right)\right)}.$$ (E8)

This solution (Eqs. (E6)-(E8)) can be rewritten in the form of Eq. (E1). To do this, choose

$${\alpha }_0=\frac{k^{+}{D}_s\left(k^{-}-e^{\beta ϵ}{k}_c^{-}\right)\left(r_0+\lambda \right)\left(r_0-{\lambda }_c\tanh \left(\frac{r_0}{{\lambda }_c}\right)\right)}{k^{-}{k}_c^{-}{r}_0\left(e^{\beta ϵ}{r}_0\lambda +{\lambda }_c\left(r_0+\lambda -\lambda e^{\beta ϵ}\right)\tanh \left(\frac{r_0}{{\lambda }_c}\right)\right)}$$ (E9)

for the solution to the reaction-limited system, or equivalently, choose

$${\gamma }_0=\frac{D_s\left(k^{-}-e^{\beta ϵ}{k}_c^{-}\right)\left(r_0+\lambda \right)\left(r_0-{\lambda }_c\tanh \left(\frac{r_0}{{\lambda }_c}\right)\right)}{r_0\left(k^{-}{r}_0\lambda +{\lambda }_c\left(r_0+\lambda -\lambda e^{\beta ϵ}\right)\tanh \left(\frac{r_0}{{\lambda }_c}\right)\right)}$$ (E10)

for the diffusion-limited system. It can be shown that denominator is not zero for any real positive D_s, k⁻, $k_c^{-}$, ε, and r₀ so this mapping is well-behaved.

In a periodic system of size L in d = 1, corresponding to the simulation examples given in the text, we have the additional constraints that the concentration is periodic in $r\left(c\left(-L∕2\right)=c\left(L∕2\right)\right)$ and ${\phantom{\mid }{\partial }_{r}c\mid }_{r=\pm L∕2}=0$ so that the concentration varies smoothly everywhere. Considering a catalytic particle centered on r = 0 and denoting the effective surface catalysis rate (in the reaction-limited scenario) as α, we have exponential solutions for the concentration profile:

$$c\left(x\right)=\{\begin{array}{cc}\frac{k^{+}}{k^{-}}-\frac{\alpha \cosh \left(x∕{\lambda }_c\right)}{{\lambda }_c{k}_c^{-}\sinh \left(r_0∕{\lambda }_c\right)}\hfill & \mid x\mid <r_0,\hfill \\ \frac{k^{+}}{k^{-}}+\frac{\alpha }{\lambda k^{-}}\left(\sinh \left(\frac{r_0-\mid x\mid }{\lambda }\right)-\coth \left(\frac{r_0-L∕2}{\lambda }\right)\cosh \left(\frac{r_0-\mid x\mid }{\lambda }\right)\right)\hfill & \mid x\mid >r_0,\hfill \end{array}\phantom{\}}$$ (E11)

where the effective surface catalysis rate is:

$$\alpha =\frac{\left(k^{+}∕k^{-}\right)\left(k^{-}-e^{\beta ϵ}{k}_c^{-}\right){\lambda }_c{e}^{r_0∕{\lambda }_c}\sinh \left(\frac{r_0}{{\lambda }_c}\right)}{1-\sqrt{\frac{k_c^{-}}{k^{-}}}{e}^{\beta ϵ}{e}^{r_0∕{\lambda }_c}\sinh \left(\frac{r_0}{{\lambda }_c}\right)\coth \left(\frac{r_0-L∕2}{\lambda }\right)}.$$ (E12)

Eqs. (E11)-(E12) completely describe the steady-state solute concentration profile in d = 1 as a function of the simulation parameters k⁺, k⁻, $k_c^{-}$, D_s, L, r₀, and ε.

Appendix F: Calculation of the force-distance and force-fluctuation relations

Here we consider the mean distance, 〈r〉, between two thermally-diffusing, chemically-inert, hard particles of radius r₀ pushed together by force F in a periodic system of length L. The mean distance diverges as F ⁻¹ as the force pushing the particles together approaches 0. According to equilibrium statistical mechanics, 〈r〉 can be found by integrating:

$$\langle r\rangle =-\frac{\partial \ln \mathcal{Ƶ}}{\partial \left(\beta F\right)}=\frac{{\int }_{2_{r0}\le r\le L∕2}{\mathit{re}}^{-\beta \mathit{Fr}}{d}^{d}r}{{\int }_{2_{r0}\le r\le L∕2}{e}^{-\beta \mathit{Fr}}{d}^{d}r}.$$ (F1)

Thus, we find:

$$\langle r\rangle =\{\begin{array}{cc}\left[2r_0+\frac{1}{\beta F}\right]+\frac{e^{2\beta }{\mathit{Fr}}_0\left(L∕2-2r_0\right)}{e^{2\beta {\mathit{Fr}}_0}-e^{\beta \mathit{FL}∕2}}\hfill & d=1\hfill \\ \left[2r_0+\frac{2}{\beta F}-\frac{2r_0}{1+2\beta {\mathit{Fr}}_0}\right]+\frac{\beta {\mathit{Fe}}^{2\beta {\mathit{Fr}}_0}\left(L∕2-2r_0\right)\left(L+4r_0+2\beta {\mathit{FLr}}_0\right)}{\left(1+2\beta {\mathit{Fr}}_0\right)\left(e^{2\beta {\mathit{Fr}}_0}\left(\beta \mathit{FL}+2\right)-2e^{\beta \mathit{FL}∕2}\left(2\beta {\mathit{Fr}}_0+1\right)\right)}\hfill & d=2\hfill \\ \left[2r_0+\frac{3}{\beta F}-\frac{2r_0\left(1+2\beta {\mathit{Fr}}_0\right)}{1+2\beta {\mathit{Fr}}_0\left(1+\beta {\mathit{Fr}}_0\right)}\right]\hfill & \hfill \\ +\frac{32r_0{e}^{\beta \mathit{FL}∕2}{(1+2\beta {\mathit{Fr}}_0\left(1+\beta {\mathit{Fr}}_0\right))}^2}{2\left(1+2\beta {\mathit{Fr}}_0\left(1+\beta {\mathit{Fr}}_0\right)\right)(8e^{\beta \mathit{FL}∕2}\left(1+2\beta {\mathit{Fr}}_0\left(1+\beta {\mathit{Fr}}_0\right)\right)-e^{2\beta {\mathit{Fr}}_0}\left(8+\beta \mathit{FL}\left(4+\beta \mathit{FL}\right)\right))}\hfill & d=3\hfill \\ -\frac{e^{2\beta {\mathit{Fr}}_0}({\left(\beta \mathit{FL}\right)}^{2}L+2r_0(2+\beta \mathit{FL}\left)\right(8+{\left(\beta \mathit{FL}\right)}^2)+2\beta {\mathit{Fr}}_0^2(32+\beta \mathit{FL}(16+\beta \mathit{FL}(4+\beta \mathit{FL}\left)\right)\left)\right)}{2(1+2\beta {\mathit{Fr}}_0(1+\beta {\mathit{Fr}}_0\left)\right)\left(8e^{\beta \mathit{FL}∕2}\right(1+2\beta {\mathit{Fr}}_0(1+\beta {\mathit{Fr}}_0))-e^{2\beta {\mathit{Fr}}_0}(8+\beta \mathit{FL}(4+\beta \mathit{FL})\left)\right)}\hfill & \hfill \end{array}\phantom{\}}$$ (F2)

where the brackets contain the value of 〈r〉 in the L → ∞ limit. In general dimension, we can concisely write:

$$\langle r\rangle =\frac{\Gamma (d+1,\beta \mathit{FL}∕2)-\Gamma (d+1,2\beta {\mathit{Fr}}_0)}{\beta F\left(\Gamma \right(d,\beta \mathit{FL}∕2)-\Gamma (d,2\beta {\mathit{Fr}}_0\left)\right)},$$ (F3)

where $\Gamma \left(n,x\right)=\left(n-1\right)!e^{-x}{\sum }_{k=0}^{n-1}\frac{x^k}{k!}$ is the incomplete gamma function [27].

Similarly, fluctuations can be calculated as

$$\langle \delta r^2\rangle =\frac{{\int }_{0\le r\le L∕2}{(2-\langle r\rangle )}^2{e}^{-\beta \mathit{Fr}}{d}^{d}r}{{\int }_{0\le r\le L∕2}{e}^{-\beta \mathit{Fr}}{d}^{d}r},$$ (F4)

which diverges as 1/(βF)² in the L → ∞ system.

Appendix G: Effective force in the diffusion-limited case

In d = 3, the concentration profile surrounding a catalytic particle with surface activity α (in the reaction-limited system) or γ (in the diffusion-limited system) is given by Eqs. (E1). In the reaction-limited case (see Appendix (G for the diffusion-limited case), the resulting radial concentration gradient is:

$${\partial }_{r}c=-\frac{\gamma (k^{+}∕k^{-})k_1\left(r∕\lambda \right)}{\lambda \left(\lambda k^{-}\right(1+\lambda ∕r_0)-\gamma )k_0\left(r_0∕\lambda \right)}.$$ (G1)

Thus, using Eq. (20), we find the characteristic force in the diffusion-limited case to be:

$$F^{\ast }=-\frac{ϵ\gamma r_0^4(r_0+2\lambda )(k^{+}∕k^{-})}{e\lambda \left(\lambda k^{-}\right(1+\lambda ∕r_0)-\gamma ){(r_0+\lambda )}^2}.$$ (G2)

This force scales as:

$$F^{\ast }\sim \{\begin{array}{cc}-\frac{ϵ\gamma r_0^5{k}^{+}}{(D_s-\gamma r_0)D_s}\hfill & r_0\ll \lambda \hfill \\ -\frac{ϵ\gamma r_0^3{k}^{+}}{(\sqrt{D_s{k}^{-}}-\gamma )\sqrt{D_s{k}^{-}}}\hfill & r_0\gg \lambda \hfill \end{array}\phantom{\}}$$ (G3)