Rejoinder

1 Scarpa, B.

The discussant raises an interesting question concerning the choice of link function. This is a common problem where the choice of link function in generalized (non)linear models has been usually based on finding the best possible fit to the data within a class of pre-specified link functions. There are guidelines available in the literature for the choice of link function in the case of binary data, along with classes of link functions including the Box-Cox transformation, skewed link functions, and generalized extreme value regression models. For instance, Chen et al. (1999) propose some graphical checks to identify the appropriate link functions. These methods can be adapted to identify the appropriate class of links that would give the best fit in our setup. Our proposed method of first posing the problem of modeling the probability of conception into a framework of a cumulative distribution function with positive support gives the flexibility of trying a wide range of parametric links that were previously unavailable. Also, a data driven approach in a nonparametric framework is definitely worth investigating in the future.

We do agree that historical data from past similar studies can be very helpful in interpreting the results of the current study. To elicit an informative prior using historical data, one can consider the power prior distribution first proposed by Chen and Ibrahim (2000) and extended for the class of generalized linear mixed models by Ibrahim et al. (2000) and Chen et al. (2003). Let D_obs = (Y, X, Z) denote current data and L(λ, β, ν₁, ${\sigma }_{\alpha }^2|D_{\mathit{\text{obs}}}$), the observed likelihood based on D_obs for our model. One can use the power prior distribution for the generalized t-link conception model as follows: suppose we have historical data from a similar previous study, denoted by D_0,obs = (Y₀, X₀, Z₀), where Y₀ is a binary pregnancy outcome, X₀ is a binary intercourse indicator, and Z₀ is the matrix of covariates based on the historical data. The power prior is defined to be the likelihood function based on the historical data D_0,obs, raised to a power a₀, where 0 ≤ a₀ ≤ 1 is a scalar parameter that controls the influence of historical data on the current data. Further, let π₀(λ, β, ν₁, ${\sigma }_{\alpha }^2$) denote the initial prior distribution for (λ, β, ν₁, ${\sigma }_{\alpha }^2$) from the previous study. Using this information, one can construct an informative prior distribution for (λ, β, ν₁, ${\sigma }_{\alpha }^2$) based on the current study as follows:

$$\pi (\mathbf{\lambda },\mathit{\beta },{\nu }_1,{\sigma }_{\alpha }^2|D_{0,\mathit{\text{obs}}},a_0)\propto L{(\mathbf{\lambda },\mathit{\beta },{\nu }_1,{\sigma }_{\alpha }^2|D_{0,\mathit{\text{obs}}})}^{a_0}{\pi }_0(\mathbf{\lambda },\mathit{\beta },{\nu }_1,{\sigma }_{\alpha }^2),$$ (1)

where a₀ can be interpreted as a dispersion parameter for the historical data. The parameter a₀ allows the investigator to control the influence of the historical data on the current study. We intend to use the priors defined here to elicit information for the newly completed LIFE Study (Buck Louis et al. 2011b).

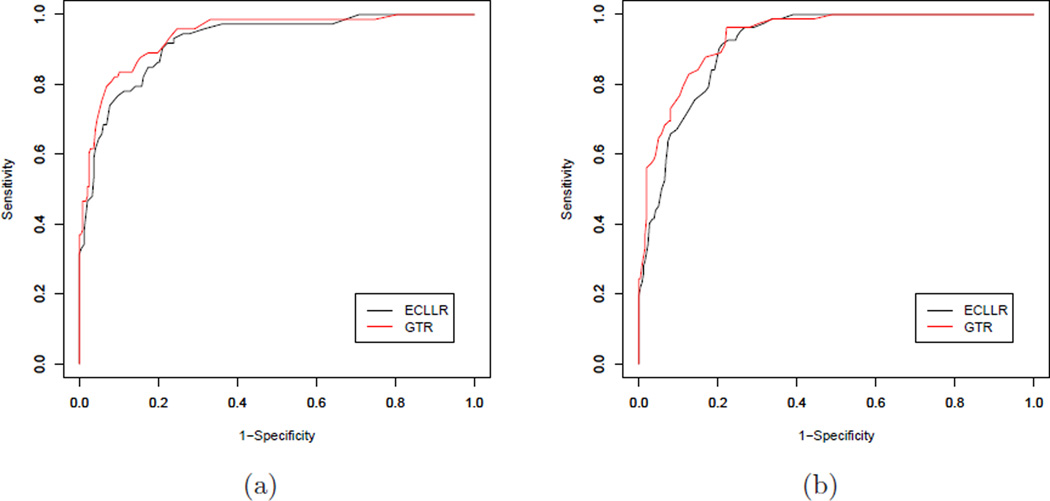
We agree with the discussant that the inclusion of non-significant covariates may have impacted our findings for the best fit model. As such, we re-ran our models by including only the “significant” covariate, i.e., parity, and had similar findings. We also investigated the models with a more “sophisticated” measure, ROC curve, and calculated the AUC and found that our findings remained.

2 Stanford, J.

The discussion raises some pertinent questions which we address below as well as gives a nice description of some of the biological aspects involved in this area.

The ease of interpretation of regression coefficients definitely is a trade-off between going for exponential link versus non-linear link functions. However as we note in our analysis, the probability of conception is impacted by the choice of the link function underscoring the importance of specifying the research question with regard to biologic plausibility and model fit.

The choice of fertile window length and its variability is a question of considerable interest to researchers assessing fecundity. Our approach in this paper has been to use the established fertile window, ranging from day −5 to 1, a window that was previously established for the Stress and TTP study, a subcomponent of the Oxford Conception Study in Buck Louis et al. (2011a). Our interest in this paper has been to investigate the impact of the choice of link functions on probability of conception in a cycle. We do intend to use the proposed model here to identify the fertile window for the newly completed LIFE Study and make comparisons with the empirically observed probability of pregnancy in the fertile window as suggested by the discussant. Also, questions such as variability in the length of the fertile window including for various population subgroups are extremely important but beyond the scope of this paper.

Figure 1.

Estimated ROC curves for exponential link conception models with the complementary log-log link (ECLLR) and the generalized t-link (GTR) based on (a) LH method; (b) OK method.

Table 1.

Model comparison under the model with only parity.

Method	Link	D(θ)	PD	DIC	LPML	AUC
LH	ECLLR	841.662	9.110	859.881	−426.131	0.923
	GTR	833.650	7.744	849.137	−416.609	0.941
OK	ECLLR	940.971	8.985	958.940	−479.532	0.917
	GTR	921.953	7.363	936.680	−462.890	0.936