Fig. 1. Fastest and simplest paths in primal and dual networks.
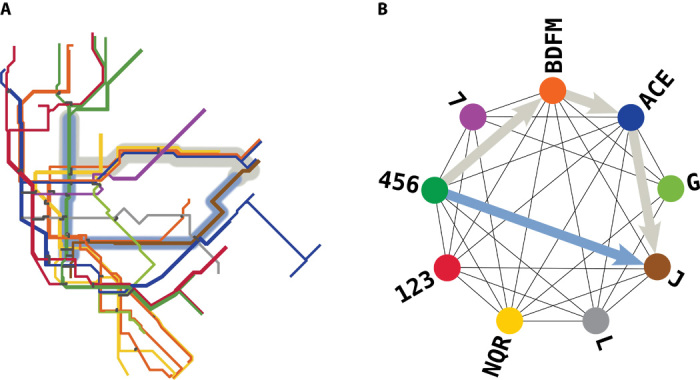
(A) In the primal network of the New York City (NYC) metropolitan system, a simplest path (light blue) from 125th Street on line 5 (dark green) to 121st Street on line J (brown) differs significantly from a fastest path (gray). There is only one connection for the above simplest path (Brooklyn Bridge–City Hall/Chambers Street) in Lower Manhattan. In contrast, the above fastest path needs three connections (5→F→E→J). We compute the duration of this path using travel times from the Metropolitan Transportation Authority (MTA) Data Feeds (see Materials and Methods). We neglect walking and waiting times. (B) In the dual space, nodes represent routes [where ACE, BDFM, and NQR are service names (49)], and edges represent connections. A “simplest path” in the primal space is defined as a shortest path with the minimal number of edges in the dual space (light-blue arrow). It has a length of C = 1 and occurs along the direct connection between line 5 (dark-green node) and line J (brown node). The above fastest path in the primal space has a length of C = 3 (gray arrows) in the dual space, as one has to change lines three times. [We extracted the schematic of the NYC metropolitan system from a map that is publicly available on Wikimedia Commons (45).]
