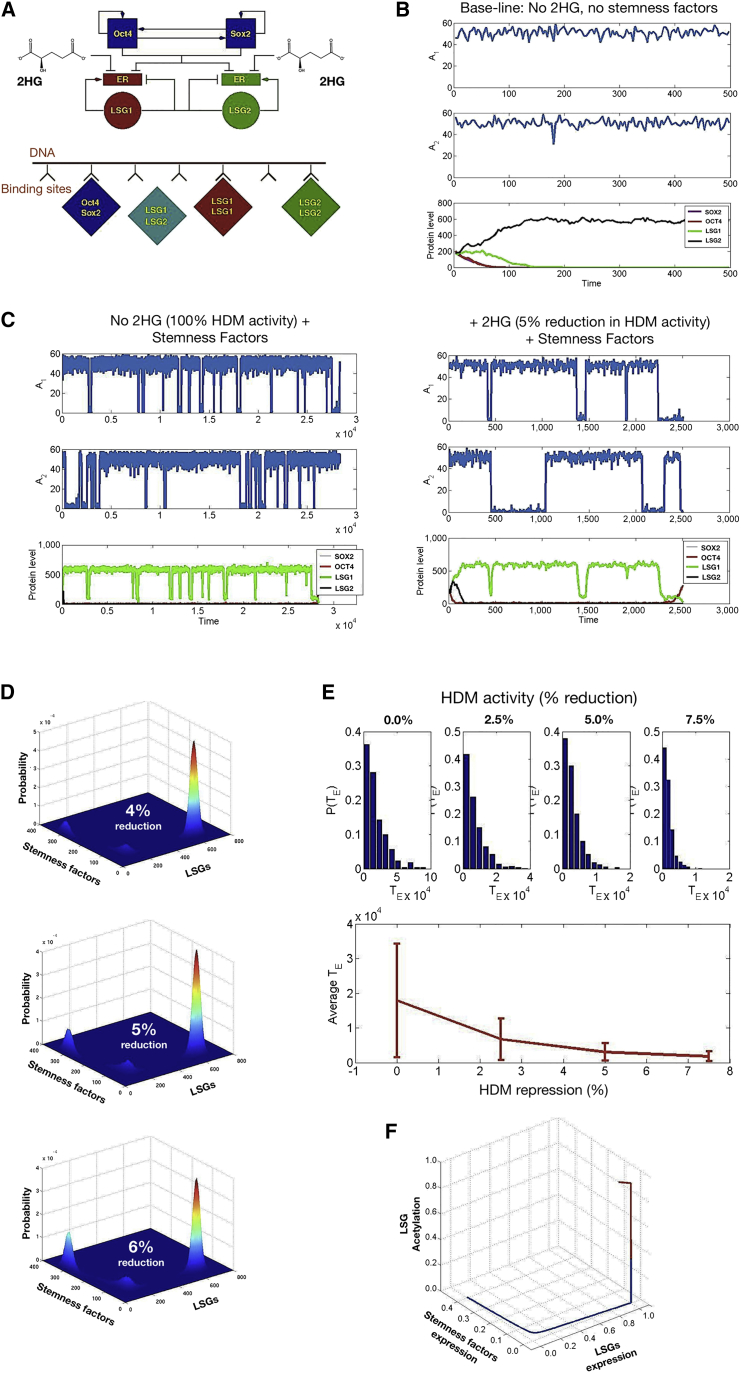
Figure 1.
Computation Simulation of Oncometabolic Nuclear Reprogramming Phenomena
(A–C) A stochastic model of oncometabolic nuclear reprogramming. (A) Top: Schematic representation of the minimal gene regulatory network considered in our stochastic model, consisting of a coupled pluripotency module (self-activation of Oct4 and Sox2) and a differentiation module (mutual antagonism between LSGs). Arrows denote activation and blunt-ended lines denote inhibitory interactions. Bottom: Schematic representation of the competitive binding model for activation/repression in the minimal gene regulatory network. (B) A realization path in which our stochastic model was run under baseline conditions (baseline HDM activity and lack of induction of stemness-related transcription factors, i.e., hi-values as per values given in Table S7 [Supplemental Appendix E] and ρ1 = ρ2 = 0). Since the system is symmetric with respect to LSG1 and LSG2, a state where O = 0, S = 0, and L2 = 0, whereas L1 > 0, is also an absorbing state. (C) A realization path in which our stochastic model was run under induction of stemness-related transcription factors (parameter values ρ1 = ρ2 = 1.85 × 107). At the onset of stemness factor induction, i.e., we let ρ1 > 0 and ρ2 > 0, the absorbing states observed in the simulations shown in (B) are not absorbing any longer and, therefore, there is a positive probability for the system to go from the differentiated cell state to the stem cell state. Left: Normal-like metabolism, baseline HDM activity; right: 2HG-induced reduction of HDM activity by 5% with respect to the baseline scenario.
(D–F) Epigenetic landscapes and reprogramming performance in response to 2HG. (D) 2HG-induced inhibition of HDM activity affects the depth of the stem cell attractors by lowering the barriers of the epigenetic landscape. Figures show the joint probability of the random variables O + S (stemness factors) and L1 + L2 (LSGs) for different values of the relative oncometabolic-induced reduction of HDM activity with respect to the baseline scenario. To obtain the epigenetic landscapes for different degrees of 2HG-induced reduction of HDM activity in shorter computational time, we considered the following parameter values: ρ1 = ρ2 = 5.55 × 10−7 and ϑo = ϑs = 0.2. We have also considered that the expression of the LSGs is induced at certain rates given by the following parameter values ρL1 = ρL2 = 2.78 × 10−7. The landscapes with 4%, 5%, and 6% reduced HDM activity correspond to h2 = 0.96, h2 = 0.95, and h2 = 0.94, respectively. The remaining parameter values are given in Table S7 (Supplemental Appendix E). (E) 2HG-induced inhibition of HDM activity affects the kinetic efficiency of the reprogramming process. The panel shows statistics of the average reprogramming time, TE, as well as its probability density, P(TE), as a function of the 2HG-induced reduction of HDM activity. The top panels illustrate that the predicted probability distribution of TE, P(TE) is approximately exponential. The lower panel shows the average and SD (error bars) of the predicted reprogramming time, illustrating that the reprogramming rate increases exponentially with the 2HG-induced reduction of HDM activity. HDM activity reductions of 0%, 2.5%, 5%, and 7.5% correspond to h2 = 1.00, h2 = 0.975, h2 = 0.95, and h2 = 0.925, respectively. (F) 2HG-induced inhibition of HDM activity affects the size of the basin of attraction of the induced stem cell state. The graphic shows a solution of the semiclassical QSSA approximation (see Equations 29–32 and 40–44 in Supplemental Information) for the baseline scenario with no HDM inhibition (h2 = 1.00, red line), and for the case with a 2HG-induced 5% reduction in HDM activity (h2 = 0.95, blue line). The uninhibited scenario converges to the differentiated cell state (red line), whereas the inhibited scenario converges to the stem cell state (blue line). Parameter values ρ1 = ρ2 = 1.85 × 107, cE1 = cE2 = 2, Co = CS = C1 = C2 = 1, and ϑo = ϑs = 0.2. The remaining parameter values are given in Table S7 (Supplemental Appendix E).