Comparing Fast Pressure Jump and Temperature Jump Protein Folding Experiments and Simulations

Abstract

The unimolecular folding reaction of small proteins is now amenable to a very direct mechanistic comparison between experiment and simulation. We present such a comparison of microsecond pressure and temperature jump refolding kinetics of the engineered WW domain FiP35, a model system for beta sheet folding. Both perturbations produce experimentally a faster and a slower kinetic phase, the “slow” microsecond phase being activated. The fast phase shows differences between perturbation methods and is closer to the downhill limit by temperature jump, but closer to the transiently populated intermediate limit by pressure jump. These observations make more demands on simulations of the folding process than just a rough comparison of time scales. To complement experiments, we calculated several pressure jump and temperature jump all-atom molecular dynamics trajectories in explicit solvent, where FiP35 folded in five of the six simulations. We analyzed our pressure jump simulations by kinetic modeling and found that the pressure jump experiments and MD simulations are most consistent with a 4-state kinetic mechanism. Together, our experimental and computational data highlight FiP35’s position at the boundary where activated intermediates and downhill folding meet, and we show that this model protein is an excellent candidate for further pressure jump molecular dynamics studies to compare experiment and modeling at the folding mechanism level.

INTRODUCTION

The detailed mechanisms of protein folding reactions are becoming amenable to a direct comparison between theory, simulation and experiment.¹ FiP35, a 35 residue hybrid of the FBP and Pin1 WW domains,² is a triple stranded beta sheet model protein with a small but well- defined hydrophobic core. FiP35 refolds very rapidly, making this WW domain a popular target for folding experiments and molecular dynamics (MD) simulation.³

Experiments indicate that at its melting temperature FiP35 is an apparent two-state folder, while well below its melting temperature it approaches downhill folding with a ‘molecular rate’ k_m=(τ_m)⁻¹=(0.7-2 μs)⁻¹.^4,5 (τ_m is approximately the time required to cross the transition state region on a coarse-grained one-dimensional free energy landscape.^5-7) Indeed, a variant of FiP35 (“GTT”), whose relaxation time of ≈3.7 μs nearly reaches the molecular time τ_m, has been experimentally characterized and simulated.⁸ Long MD trajectories at T_m reveal a low barrier, consistent with experiments at T_m. The computed barrier lies between 1 and 5 kT on a one-dimensional free energy surface, depending on the analysis.^4,5,9,10 MD trajectories well below T_m are not yet available for direct comparison with experiment.

A one-dimensional description is not complete. For example, implicit solvent simulations of the Beta3s peptide (structurally similar to the WW-domain), reveal two parallel folding pathways¹¹ where either hairpin 1 or hairpin 2 forms first. As another example, Markov analysis of multiple WW-domain folding trajectories near T_m reveals complex kinetics among multiple short-lived intermediates.¹² Thus, the experimentally measured molecular time τ_m probably lumps together into one number a complex network of fast processes whose 0.7-2 μs time scale collectively accounts for the time required to cross the transition state region on a rough free energy landscape.

The power of all-atom molecular dynamics (MD) simulations to illuminate protein folding experiments remains limited by time scale: It is computationally expensive to integrate the equations of motion for tens of thousands of atoms over the complete duration of protein refolding.⁹ Until recently, only temperature jump-induced kinetics (T-jumps) were quick enough to compare with single-trajectory simulations.^13,14 Now instrumentation improvements have enabled microsecond resolution pressure jump experiments (P-jumps).^15-17

Here we present a unified study of microsecond P-jump and T-jump experiments of FiP35. Experiments reveal two distinct microsecond kinetic phases in both types of jumps, but the faster phase behaves differently in the P-jump than in the T-jump. We complement the experimental data with all-atom MD simulations that fairly closely mimic the actual P- and T-jump experiments: the protein is unfolded either by pressure or heat, allowed to equilibrate, and then jumped back to the original temperature or pressure, whereupon relaxation is observed. Several P- and T-jump trajectories lead to complete refolding of FiP35, allowing us to gather some statistics about mechanism. Our modeling using Bayesian analysis of the MD trajectories¹⁸ and kinetic master equations shows that simulation is in good agreement with the experimentally observed kinetic curves. Although some reasonable assumptions have to be made about the fluorescence signal of the intermediates, and the agreement thus does not prove the mechanism extracted from the MD simulations, our results show that MD can reproduce complex experimental kinetics with multiple time scales quantitatively. This is an important step forward in using the combination of experiment and simulation to understand protein folding mechanisms in detail.

METHODS

Sample preparation

FiP35 was expressed in E. coli BL21 (DE3 RIPL, Agilent) cells, and purified as described previously⁵ and in the SI. The purified FiP35 was lyophilized and re- suspended to a final concentration of 200-400 μM in 100 mM sodium phosphate buffer, pH 7.0. Buffer conditions were identical throughout all experiments while concentrations of FiP35 and GuHCl varied. FiP35’s single tryptophan on the first beta strand (loop or hairpin 1) enabled monitoring of folding via fluorescence, in particular the formation of strands 1 and 2.

Pressure, temperature and denaturant unfolding thermodynamics

FiP35 unfolding at high pressure and temperature were measured on a fluorimeter. The unfolding reaction was monitored by tryptophan fluorescence emission spectra. As described previously¹⁷ and in the SI, a pressure cell (ISS) was used for the pressure denaturation at 50 or 100 μM FiP35 concentration. A temperature-controlled sample holder (Agilent) was used for the temperature denaturation at 10 μM FiP35 concentration. For temperature measurements, the lower concentration was necessary to measure complete thermal denaturation curves above 60 °C where FiP35 aggregates at concentrations above 50 μM. FiP35 also denatures and refolds reversibly at 300 μM across the temperature and pressure ranges of the kinetics experiments (see SI Figures 1 and 2). Because FiP35’s fold is so stable, pressure and temperature melts were performed from 0 M up to 4 M (for temperature) or up to 5 M (for pressure) guanidinium hydrochloride (GuHCl), buffered to pH 7. Both pressure and temperature unfolding thermodynamics were analyzed using singular value decomposition (SVD¹⁹). Although FiP35 is not an ideal two-state folder, we were able to fit its temperature-denaturant unfolding globally with a two-state unfolding model (see SI). Thermodynamic parameters from the global fits were used to calculate the folding free energy ΔG and effective equilibrium constant K_eq=exp(−ΔG/RT) of the final equilibrium state reached in both T-jumps and P-jumps: 23 °C, 0.1 MPa, and various GuHCl concentrations.

P-jump and T-jump kinetics

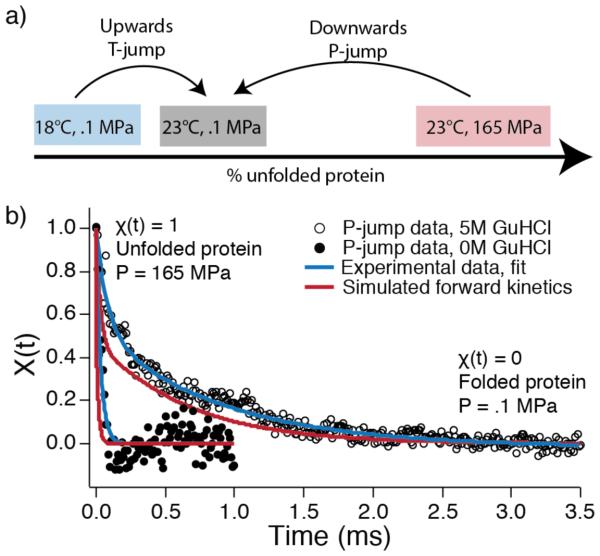
P-jump kinetics were measured at 23 °C as described previously^15,17 and in the SI with a home-built fast pressure drop apparatus capable of pressure drops up to 250 MPa with a dead time of about a microsecond. The P-jump also slightly drops the temperature due to adiabatic cooling.¹⁵ T-jumps from 18 °C to 23 °C were carried out as described previously²⁰ with a Surelite Q-switched Nd:YAG laser (Continuum) Raman-shifted to 1.9 μm and sent through a 50/50 beam splitter such that the sample is heated from two sides. In both P-jump and T-jump measurements, FiP35 solutions of 300 μM in various concentrations of GuHCl were assayed. FiP35 was jumped to the same final thermodynamic state in T- and P- jumps (figure 1a), enabling direct comparison of the measured kinetics.

Figure 1.

Experimental scheme and kinetic traces. a) Temperature and pressure were jumped to the same final condition, thus allowing their rates to be compared. At low GuHCl concentration, both observed kinetic rates monitor predominantly refolding kinetics. b) Two representative P-jump traces at 0 M or 5 M GuHCl. Both traces have been binned to 5 μs intervals. Blue curves show double exponential fits to the experimental data. Red curves are the kinetics from a ‘two parallel intermediates’ master equation model (model IV in Figure 5a) populated with rates from MD trajectories. Simulated kinetics are scaled to account for the viscosity difference between simulated and experimental water, and the 5 M GuHCl is also scaled by the experimental k_{0 M}/k_{5 M} ratio of rate coefficients (see SI methods).

For both P- and T-jumps, tryptophan fluorescence lifetime decays were probed every 12.5 ns before, during, and after the jump by a mode-locked Ti:Sapphire laser (KMLabs) that was frequency-tripled to 280 nm. 50 fluorescence decays in each jump were binned before analysis. Plots shown throughout the text are further smoothed and binned to 5 μs per point.

Data analysis for kinetic experiments is described in detail in the SI. Briefly, the change of tryptophan fluorescence decays f over the course of the reaction was quantified by linear decomposition into two components f₁ (beginning of jump) and f₂ (after equilibrium has been re-established post-jump).²¹ In the general linear decomposition f=a₁(t)f₁+a₂(t)f₂+^…, more than two components were not found necessary to account for the data within the measured signal-to-noise ratio. χ(t)=a₁(t)/(a₁(t)+a₂(t)) ranges from 1 at the beginning of the jump to 0 at the end of the jump, and the decay of χ(t) following the P- or T-jump is fit to a double-exponential. Two representative P-jumps at different concentrations of GuHCl are shown with double-exponential fits in figure 1b.

Although FiP35 is not a two-state folder, the separation of fast and rate-limiting time scales (≥ 3) is large enough for a two-state analysis of the rate-limiting step to be useful. It can be used to estimate the refolding rate at 0 M GuHCl (simulation condition) for T-jump experiments, and to assess whether the higher concentration GuHCl experiments extrapolate to the experimentally measured 0 M GuHCl P-jump refolding rate. Activated folding rate coefficients and unfolding rate coefficients were calculated for each GuHCl concentration as k_f=k_obsK_eq/(1+K_eq) and k_u=k_obs/(1+K_eq), where k_obs is the observed rate coefficient of the slow kinetic phase (rate-limiting activated folding step). The thermodynamic parameters from the pressure-probed unfolding were used to calculate folding and unfolding rates for P-jumps and those from the temperature-probed unfolding were used for T-jump calculations. The resulting chevron plot folding and unfolding arms were fit to lines in order to extrapolate the expected folding/unfolding rates at 0 M GuHCl.

Molecular Dynamics Simulations

Molecular dynamics simulations, described in detail in the SI, were performed in explicit solvent using the TIP3P water model²² and the CHARMM22* force field for the protein.²³ The structure of the WW domain (FiP35 mutant, residues 4 to 38) from the protein data bank (PDB code 2F21)² was placed in a cubic box of 10,232 water molecules and neutralized with 6 sodium ions and 9 chloride ions employing VMD.²⁴ All simulations were carried out with periodic boundary conditions in a constant particle number, temperature, and pressure ensemble (NPT). Starting from the native state of the protein, two types of simulations were performed: P-jump and T-jump. Unfolding simulations were performed using NAMD²⁵, and refolding simulations were performed on the Anton Platform.^26,27 Data analysis and figure rendering were done using VMD.²⁴

In a P-jump simulation, pressure was increased from 0.1 MPa to 900 MPa in 0.3 μs at a rate of 0.9 MPa/300 ps, followed by a 1-μs high-pressure equilibrium simulation (P = 900 MPa) and a pressure-drop simulation in which pressure was jumped downward from 900 MPa to 0.1 MPa in 0.3 μs at a rate of -0.9 MPa/300 ps. The temperature was maintained at T = 325 K through the P-jump simulation. In a T-jump simulation, the pressure was maintained at P = 0.1 MPa throughout the simulation and the system was heated up to 400 K for 1 μs between the initial 100-ns equilibrium simulation and the final refolding simulation, both at T = 325 K. To generate multiple refolding trajectories, the pressure or temperature unfolded state was equilibrated for an additional 200 ns, during which the structures were taken at t = 0 ns, 100 ns, and 200 ns to continue the P-jump or T-jump simulations at ambient conditions. The simulated and experimental P-jumps are in the same direction, although the denaturation pressure is higher in simulations to facilitate rapid unfolding. Note that both P- and T-jump simulations leave the WW domain under strong refolding conditions, as is also the case in the experiments (T=23 °C, P=0.1 MPa), although the simulated and experimental T-jumps are in opposite directions.

Kinetic mechanism modeling

Our main focus here is comparing the novel P-jump experiments and simulations. We started with a Bayesian analysis¹⁸ to estimate from the P-jump MD simulations the rate coefficients connecting the unfolded state to intermediate states and intermediate states to the native state. Because the P-jump simulations (and the experiments) were carried out under conditions strongly favoring the native state, we assume that reverse rate coefficients are negligible (see SI).

Next, we tested four different kinetic models (Figure 5a) that are minimally consistent with experiment and simulation (i.e. they can yield a double exponential decay). To assess whether the models were consistent with experimental data, kinetic master equations were solved via numerical integration with the rate coefficients obtained from the Bayesian analysis of MD trajectories. The output of these simulations is the concentration of each state in each model as a function of time.

Figure 5.

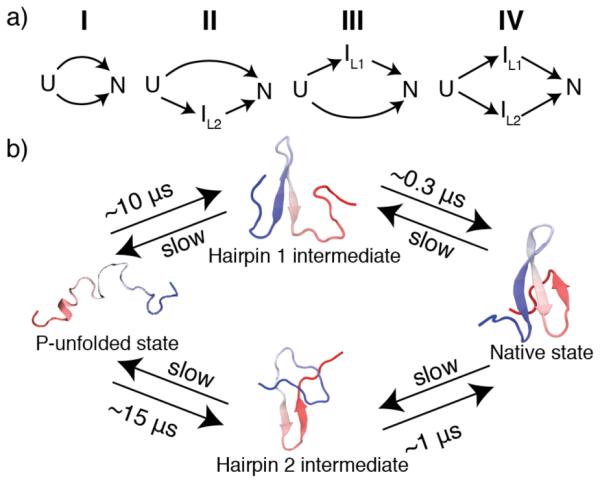
Kinetic models. (a) Mechanisms tested by master equation kinetics and compared with experiment. (b) Mechanism describing folding behavior of FiP35 following P-jump that is consistent with both experiment and simulation. Forward rates were estimated via Bayesian analysis from MD simulations.¹⁸

The shape of the observed kinetic decay also depends on the fluorescence decay signal of intermediate states in the kinetic scheme. Given that the tryptophan residue of FiP35 is located between strand 1 and strand 2 it is reasonable to assume that all measureable signal in our experiment arises from the formation of the hairpin 1 intermediate or the native state. Thus, signal functions composed of the time evolution of the concentration of the hairpin 1 intermediate plus the native state or the native state alone were tested.

To assess each model/signal function combination, each simulated kinetic trace was fit to a double exponential. The fitted fast phase amplitude, fast phase rate, and slow phase rate were compared to those obtained from experiment via linear least squares. We then ranked the simulations quantitatively by their ability to reproduce the double exponential shape of the experimental data in Fig. 1b.

To account for computed vs. experimental viscosity and overall barrier heights, the simulated kinetic traces were scaled by the known literature ratio of experimentally measured FiP35 folding rates to those determined in silico from simulations also on the Anton computer (see SI).⁹ Our simulations are in 0 M GuHCl and thus can be compared directly to the 0 M GuHCl experimental data in Figure 1b. To compare simulations to higher GuHCl concentration experimental data, the simulation was scaled by the experimental ratio of the slow phase folding time with and without GuHCl. Thus, the two simulated traces in Fig. 1b represent the comparison of a single kinetic model with experimental data obtained under fast (no GuHCl) and slow (with GuHCl) folding conditions.

RESULTS

FiP35 is thermodynamically stable to temperature and pressure denaturation

Unfolding of FiP35 with pressure, temperature and denaturant (GuHCl) was measured by monitoring fluorescence from its single tryptophan residue. FiP35 unfolds reversibly up to 90 °C at concentrations ≤ 50 μM⁵ and up to 210 MPa at ≤ 100 μM (SI Figure 1). At the highest pressures and temperatures used in kinetics experiments, no concentration dependence of the thermodynamics were observed and FiP35 was fully reversible at a concentration of 300 μM (SI Figure 2). When FiP35 is destabilized, its activation barrier increases, and its unfolding can be fitted approximately to a two-state model⁵, yielding its melting temperature and pressure (SI methods, SI Figure 3, SI table 1). FiP35 has an extremely stable fold: with no added GuHCl, the pressure unfolding midpoint is ≈680 MPa (SI table 1).

Due to FiP35’s deviations from two-state behavior, fitted melting temperatures vary depending on how the fluorimeter data is analyzed. Here, singular value decomposed (SVD¹⁹) fluorescence spectra plotted versus temperature give a melting temperature close to 90 °C. When the same data is expressed as an integrated fluorescence intensity versus temperature, the fitted melting temperature is 75 °C, consistent with previous measurements.^4,5 Here we use SVD to analyze the spectra in order to avoid intensity contributions to the signal, which in our pressure thermodynamics instrumentation can contain artifacts (see SI).

P- and T-jump kinetics are bi-exponential

Pressure-drop-induced refolding kinetics were measured at various GuHCl concentrations using a home-built apparatus that delivered a 165 → 0.1 MPa downward P-jump at 23 °C with an instrument dead time of about 1 μs.¹⁵ To compare P- and T-jump folding kinetics, 5 °C T-jumps were performed from 18 to 23 °C, the same final state as the P-jumps (Figure 1a). In both P- and T-jumps, the reaction was monitored by tryptophan fluorescence lifetime.⁵

Both T- and P-jump kinetics reveal a faster kinetic phase (≈6 μs for T-jump, 11-21 μs for P- jump; SI tables 2 and 3, SI Figure 4 and 5) and a slower kinetic phase (200-500 μs; SI tables 2 and 3, SI Figure 4 and 5). The ‘slow’ P-jump phase is much faster than the previously observed millisecond P-jump refolding of λ_6-85, which was attributed to pressure-induced trapping in a highly helical non-native state.¹⁷ There is no evidence of such millisecond traps in pressure-induced refolding of FiP35, making it attractive for full-atom simulations of complete refolding.

The slow kinetic phase is similar between perturbation methods

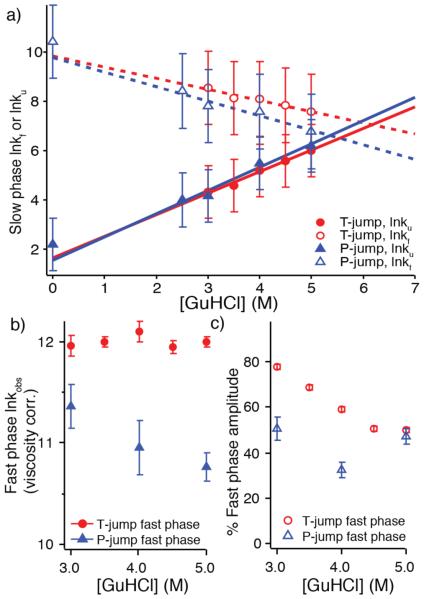
The slow kinetic phase in both T- and P-jump is consistent with being FiP35’s activated refolding phase. Both experiments in low or 0 M GuHCl and 23 °C are under conditions strongly favoring the native state. Kinetic and thermodynamic data were combined in a two-state analysis to extract folding and unfolding rates for the slow phase, an approximation given the observation of an additional fast phase (discussed below). The chevron plot in Figure 2a shows that the denaturant dependence of both folding and unfolding rates is similar for T- and P-jump kinetics, although T-jump-probed folding rates are somewhat faster. All assayed GuHCl concentrations are below the GuHCl titration midpoint of FiP35,²⁹ resulting in the expected decrease in the folding rate and increase in the unfolding rate with increasing GuHCl concentration.

Figure 2.

Experimental kinetics summary. a) Chevron plot illustrating the GuHCl dependence of the slow phase folding and unfolding rates. Rates are linearly extrapolated without viscosity correction.²⁸ Error bars include fit error from thermodynamic values and standard error from averaging kinetic fit parameters. b) Observed, solvent viscosity scaled relaxation rate of the fast phase for T- and P-jump (k in units of s⁻¹, ln is the natural logarithm, error is standard error). c) The percentage of the amplitude corresponding to the fast phase. For both b) and c), error is standard error from averaging fitted values across multiple experimental traces.

Linear extrapolation of the activated folding rates versus GuHCl concentration yields activated folding rate coefficients k_f of (56 μs)⁻¹ for P-jump and (52 μs)⁻¹ for T-jump at 23 °C in the absence of denaturant. A P-jump of FiP35 without denaturant (Figure 1b, SI Figure 6) yielded a fitted folding rate coefficient of (29.5 μs)⁻¹, within measurement error of the extrapolation (Figure 2a). The T-jump activated rate was previously measured only above 60 °C,⁵ where k_f≈(20 μs)⁻¹ is faster than our extrapolated value of (52 μs)⁻¹ at 23 °C. The previous measurements cover a wide temperature range above 60 °C,⁵ and their extrapolation to room temperature in absence of GuHCl agrees well with our current measurements at room temperature extrapolated to 0 M GuHCl.

The fast kinetic phase differs between perturbation methods

Unlike the slow phase, the fast kinetic phase of FiP35 behaves differently after T- and P-jump (Figure 2b, 2c). Like the slow phase, the P-jump fast rate decreases as GuHCl concentration increases, even after viscosity correction (Figure 2b); its amplitude shows no obvious trend when the GuHCl concentration is changed (Figure 2c). In contrast, the fast T-jump rate has no GuHCl concentration dependence, even after viscosity correction (Figure 2b), and its amplitude clearly increases when FiP35 is stabilized by removing denaturant (Figure 2c). In addition, the T-jump fast phase also has a rate (6 μs)⁻¹ at 23 °C that is about 2-3 times faster than the P-jump fast phase and approaches the folding “speed limit”³⁰ previously measured for FiP35 in the (0.7-2 μs)⁻¹ range between 60- 85 °C.^4,5

FiP35 completely refolds in several P- and T-jump simulations

We ran six long single- trajectory all-atom MD simulations for FiP35 to provide mechanistic information to complement experiment. Two types of simulations of unfolding were performed, high temperature and high pressure, followed by a jump to ambient conditions where refolding ensued. Three refolding trajectories for each denaturation type were obtained yielding over 70 microseconds of refolding trajectories in total.

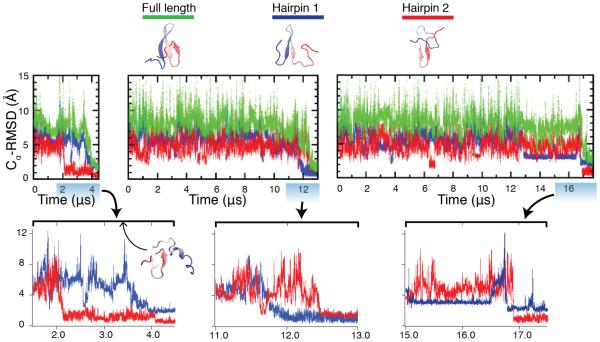
The P-jump simulations mimic the experimental protocol. A pressure of 900 MPa, which exceeds the experimentally determined unfolding midpoint, was used to unfold the protein. During the unfolding process, hairpin 2 lost its native structure first, followed by the denaturation of hairpin 1, as shown in SI Figure 7a and 8a. Across the three refolding simulations (Figure 3, SI Figure 9), the protein refolded into the native state in 4 μs, 12.5 μs, and 17.5 μs.

Figure 3.

Structural characterization of the refolding trajectories following P-jump, at T=325 K and P= 0.1 MPa, from the pressure-denatured state. C_α-RMSD values have been calculated relative to the crystal structure (PDB:2F21).² Hairpin 1 contains residues 11 to 25 and hairpin 2 contains residues 22 to 33. Structures under the legend show the native structure, a hairpin 1 formed (or loop 1) intermediate, and a hairpin 2 formed (or loop 2) intermediate. The full length C_α-RMSD values are calculated using residues 7 to 35. Bottom: Highlights of the folding transitions. Inset structure in the first folding transition is a misfolded structure with mirror image topology (see main text).

Two different folding mechanisms were observed in the simulations with one simulation folding through hairpin 2 first, and the other two through hairpin 1 first. The persistence of the hairpin 2-containing structure (representative structures shown in figure 3 under the legend) for several microseconds before refolding to the native state may arise from the formation of a mirror image topology where hairpin 1 begins to form on the wrong side of hairpin 2 (inset structure in bottom panel of Figure 3)—a kinetic trap arising from the energetic similarity between the native state and the mirror image topology that has been observed theoretically and experimentally in symmetrical proteins.³¹

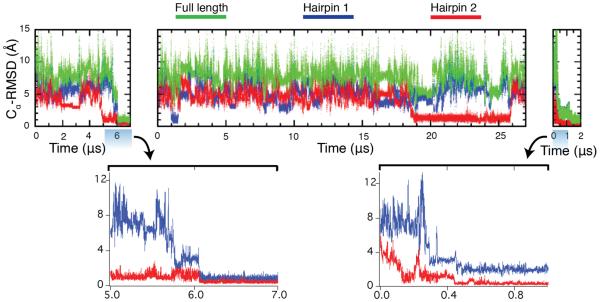
T-jump simulations were also performed. A high temperature of 400 K was used to simulate temperature denaturation of FiP35 (SI Figure 7b and 8b). The protein unfolded in 50 ns by losing both hairpins almost simultaneously. Upon return to room temperature, the protein folded to its native state in 0.5 and 6 μs, hairpin 2 first. In one simulation, FiP35 formed hairpin 2 in 19 μs but failed to fold in 27 μs of simulation (Figure 4, SI figure 10). Note that while the simulation is a downward T-jump and the experiment upward, the experimental final condition, as in the P-jump, is under conditions very strongly favoring the native state (23 °C, far below previous experimental studies carried out at 50+ °C).

Figure 4.

Structural characterization of the refolding trajectories following T-jump, at T=325 K and P= 0.1 MPa, from the temperature-denatured state. C_α-RMSD values have been calculated relative to the crystal structure (PDB:2F21).² Hairpin 1 contains residues 11 to 25 and hairpin 2 contains residues 22 to 33. The full length C_α- RMSD values are calculated using residues 7 to 35. Bottom: Highlights of the folding transitions.

Kinetic modeling suggests a parallel four-state folding mechanism following P-jump

The P-jump simulations revealed two paths to the native state following pressure jump: folding through hairpin 1 first or hairpin 2 first. We used Bayesian analysis of the molecular dynamics trajectories and kinetic master equations to determine the kinetic mechanism that best matches both MD simulation and experiment. Two parallel mechanisms, models III and IV in figure 5a, were in excellent agreement with experiment when fluorescence of the hairpin 1 intermediate is included in the signal function and kinetics are scaled to account for the known viscosity difference between actual and simulated water (see SI and SI figure 11 for scoring of these models and detailed discussion of the other tested models).³² One of these two mechanisms is most consistent with simulation: a slower path to the native state through hairpin 2 and a parallel faster path through hairpin 1 as illustrated in figure 5b. Figure 1b shows the very close agreement between this model (red traces) and the experimental data (black circles).

DISCUSSION

We present here an experimental comparison of T- and P-jump refolding on the microsecond time scale and simulate T- and P-jump protocols in all-atom molecular dynamics simulations. In particular the P-jump protocol is similar in experiment and simulation, although a higher denaturation pressure was used in the simulation to accelerate unfolding. FiP35 has been shown previously to fold following T-jump on a molecular dynamics-friendly timescale.^4,5 Unlike the only other microsecond folder previously analyzed by P-jump,^16,17 lambda repressor, which exhibited a slow millisecond phase in addition to a fast phase, we see that P-jump folds FiP35 on a microsecond time scale. For the most direct comparison with simulation, we were also able to obtain refolding data in the absence of any denaturant where folding occurred with a rate below (30 μs)⁻¹. This fast folding behavior makes FiP35, and other fast WW-domain mutants such as GTT,⁸ excellent candidates for future P-jump experimental and computational studies.

Experimentally, FiP35’s refolding kinetics are bi-exponential when probed by both temperature and pressure. The slow phase, on the scale of hundreds of microseconds depending on GuHCl concentration, is very similar between T- and P-jump, showing comparable rate dependence on denaturant concentration and similar folding and unfolding rates. While the phase shows similar characteristics in both experiments, this does not guarantee that the folding mechanisms are identical between perturbation methods.

The fast phase, on the other hand, exhibits clearly different kinetic characteristics between the two perturbation methods, so the folding mechanism following P- and T-jump differs on the fastest time scales. The T-jump fast phase rate at 23 °C (over 50 °C below T_m) approaches the folding speed limit, shows no dependence on GuHCl concentration when adjusted for viscosity, and exhibits an increase in amplitude as solvent conditions become more stabilizing—the combination of these behaviors has been interpreted as a signature of downhill folding.^1,5,33 Considering this data and previous work demonstrating FiP35’s downhill folding behavior under strongly native state-promoting conditions,^4,5 we assign the fast phase of FiP35 following T- jump as the “molecular” or “downhill” phase. No previous simulations are available under these conditions. Downhill kinetics occur when the folding barrier along a 1-D free energy profile is very low, so some population exists at the barrier top. This barrier-top population reacts promptly after T-jump and is followed sequentially by activated folding of population in the unfolded free energy well. On a multi-dimensional free energy surface, such prompt kinetics may correspond to a complex ensemble of transiently populated states, as seen in Markov modeling and other analyses of beta sheet folding.¹²

In contrast, (1) the P-jump fast phase has a slower rate of (11-21 μs)⁻¹; (2) the rate decreases more upon addition of GuHCl than expected from increased solvent viscosity, indicating a barrier whose height increases with denaturant concentration; and (3) there is no discernible trend in the fast phase amplitude. These three behaviors are not consistent with downhill folding. Short-lived intermediate(s) on the unfolded side of the main barrier are the simplest explanation, although other kinetic scenarios, such as differences between the presssure and temperature unfolded states, are also possible.

The difference in folding mechanism between pressure- and temperature-jump folding that we observe experimentally is reflected in the MD simulations, where P-jump showed a more heterogeneous folding mechanism than T-jump. Our P-jump folding mechanism—folding through either hairpin 1 or hairpin 2—is remarkably consistent with experiment, as demonstrated through direct comparison of the kinetic model with the experimental data (Fig. 1b). Of course, our model is just the simplest consistent with the experimental and simulation data, and even more detailed probes could reveal additional complexity.

The mechanism allowing both hairpin 1 or hairpin 2 to fold first is generally in agreement with scenarios reported in the literature when FiP35 is started in the unfolded state under native conditions.^{9,10,12,34,35} Markov state models proposed a heterogeneous folding mechanism, with one group finding four folding paths³⁴, including folding through both hairpin 1 and hairpin 2, and another group finding that folding proceeds 70% of the time through hairpin 1 and 30% of the time through hairpin 2.³⁵ Interestingly, the only all-atom MD simulation where FiP35 ultimately folded (prior to the work presented here) was interpreted by a folding mechanism where hairpin 1 exclusively formed first—a folding order that was attributed to the greater thermodynamic stability of the isolated hairpin 1.⁹ Re-analysis of that data by another group found that 80% of the time hairpin 1 folded first and 20 % of the time hairpin 2 was the one to fold first.¹⁰

Our work and these previous simulation results suggest that folding of FiP35 via both paths can occur following both P-jump and T-jump. Although in similarly structured peptides partitioning between parallel folding pathways was enhanced by sequence similarity between hairpins³⁶, this does not appear to be the case for FiP35 (see SI). Most likely, the significant population of both folding pathways can be attributed to a combination of similar thermodynamic stability and kinetic accessibility of the two partially folded intermediates. All of these results are consistent with the original observation that hPin1 WW domain (the precursor of FiP35 with a longer loop 1) has large Phi values in loop 1, and smaller but not-zero Phi values in loop 2³⁷: In hPin1 WW domain, formation of loop 1 is the rate-limiting step, but when loop 1 is replaced by the shorter FBP WW domain loop, both loops can fold on a more similar time scale.

Although folding times from T-jump experimental data have been compared to folding times from MD simulations,¹ pressure perturbation offers an additional constraint through which force- fields can be tested. Our combination of computational and experimental results highlight three interesting aspects of FiP35’s folding behavior: (1) P-jump refolding is complete in 10s of μs, an MD-friendly time scale. (2) When perturbed by temperature and pressure, FiP35 lies in the gray zone of the transition between downhill folding and multi-state folding through short-lived intermediates. That is, by T-jump the fast phase shows characteristics explained by the breakdown of transition state (Kramers) models discussed in detail previously.³⁰ By P-jump, the fast phase has characteristics that strongly support a short-lived intermediate—behavior that is reflected in some MD simulations.³⁸ (3) MD simulations of the P-jump induced refolding of FiP35 very closely match our experiment when the appropriate kinetic model is chosen. This remarkably close agreement allows us to assign a parallel kinetic mechanism for FiP35’s folding following pressure drop (Figure 5b).