Modulating Enzyme Catalysis through Mutations Designed to Alter Rapid Protein Dynamics

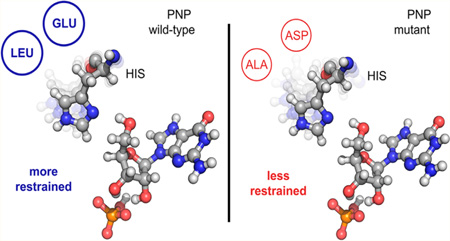
Abstract

The relevance of sub-picosecond protein motions to the catalytic event remains a topic of debate. Heavy enzymes (isotopically substituted) provide an experimental tool for bond-vibrational links to enzyme catalysis. A recent transition path sampling study with heavy purine nucleoside phosphorylase (PNP) characterized the experimentally observed mass-dependent slowing of barrier crossing (Antoniou, D.; Ge, X.; Schramm, V. L.; Schwartz, S. D. J. Phys. Chem. Lett. 2012, 3, 3538). Here we computationally identify second-sphere amino acid residues predicted to influence the freedom of the catalytic site vibrational modes linked to heavy enzyme effects in PNP. We mutated heavy and light PNPs to increase the catalytic site vibrational freedom. Enzymatic barrier-crossing rates were converted from mass-dependent to mass-independent as a result of the mutations. The mutagenic uncoupling of femtosecond motions between catalytic site groups and reactants decreased transition state barrier crossing by 2 orders of magnitude, an indication of the femtosecond dynamic contributions to catalysis.

Graphical Abstract

INTRODUCTION

Understanding the dynamic interactions at enzyme catalytic sites to achieve chemical function is still a partially unmet goal. In this Article, we use a computational technique (transition path sampling and reaction coordinate identification) to explore protein design related to heavy-enzyme isotope effects and fsec coupling between the catalytic site and reactants. We test the computational design experimentally.

The importance of femtosecond (fs) motions in reaching the transition state in enzymatic reactions has gained acceptance,^1,2 but it is not a universal phenomenon in all enzymes (e.g., for at least one system, it has been shown that such motions are not present³) and there are also reasonable opinions that hold the opposite view.⁴ An experimental probe that has been useful in elucidating the relevance of fast protein motions on catalysis is isotope replacement in the protein body of the enzyme,⁵ where heavy atoms are substituted in all or parts of the protein. The change in atomic masses alters vibrational frequencies, while the potential energy surface and electrostatic properties are minimally perturbed or unaltered.

In earlier computational⁶ and experimental⁷ work, we studied the dynamics of heavy purine nucleoside phosphorylase (PNP). PNP catalyzes the phosphorolysis of the N-ribosidic bond of 6-oxypurine nucleosides and deoxynucleosides and is the only route for degradation of deoxyguanosine in humans. Human genetic deficiency in PNP leads to T-cell mediated immune suppression causing autoimmune deficiency, while inhibition of PNP is therapeutic for T-cell leukemia, lymphoma, and rejection of transplants.^8,9 Thus, PNP is an established target for drug development.^10–14

In heavy PNP, the amino acids are uniformly labeled with ¹³C, ¹⁵N, and nonexchangeable ²H. Heavy isotopes perturb the bond vibrations without affecting the electrostatics of the protein and reduce the rate of the enzymatic chemical step.⁷ In native PNP, a motion of His257 near the active site causes compression of three reaction coordinate oxygens, an important feature for transition state (TS) formation. In earlier work we found that in the heavy enzyme this motion is mistimed and leads to a less frequent formation of the TS. The goal of the present work is an attempt to explore this mistiming by second-sphere mutations to alter catalytic site dynamics. We set out to identify mutations in the heavy enzyme that restore the timing of the compression of the reaction coordinate oxygens caused by His257 motion. This is a first step in employing protein dynamics as part of an enzyme design principle.

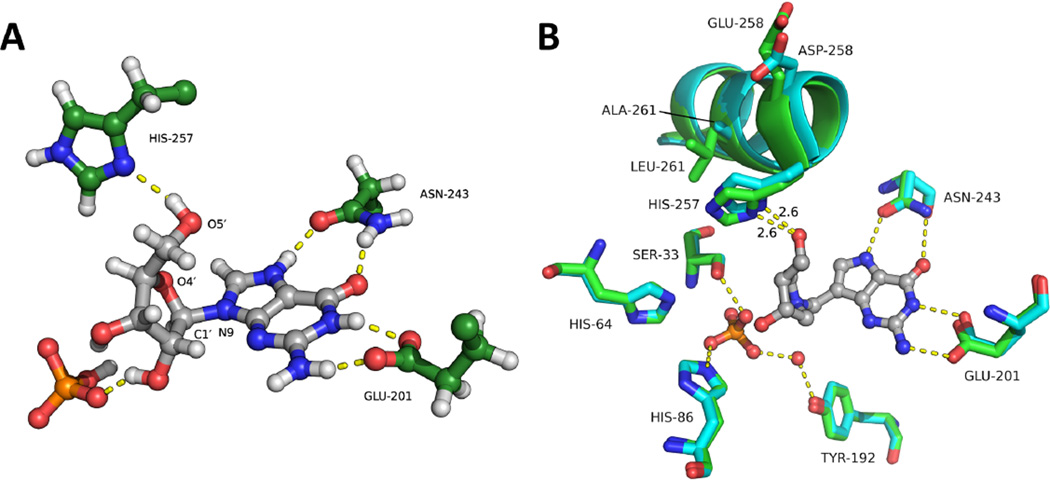
The mechanism of the PNP reaction^16,17 involves promotion of ribocation formation and leaving group activation (Figure 1A). His257 compresses O5′ toward the O4′ of the purine ring, which destabilizes ribosyl electrons into the purine leaving group. Loss of electrons from the O4′ to form a partial double bond with C1′ causes rehybridization of the N-ribosyl carbon toward sp² geometry. The loss of bonding electrons to the purine causes an electron rich purine, neutralized prior to transition state formation by N7 protonation. Loss of the N-ribosidic bond causes C1′ migration toward an anionic oxygen (O_p) of the phosphate to complete product formation. Residues Asn243 and Glu201 are essential to protonate, neutralize and stabilize the purine leaving group. Observations from crystallographic data, kinetic isotope effect analysis¹⁵ and QM/MM molecular dynamics simulations¹⁸ showed that a geometric compression of the three oxygens O5′, O4′, and O_p, essential for product formation, is caused by His257 motion (Figure 1A). Atomic details of how the His257 motion facilitates the reaction have been identified in earlier computational work⁶ by examining the time series of atomic positions as the TS is formed. The motivation of the work reported here is an attempt to modulate enzyme function via mutation that causes changes in rapid catalytic site protein dynamics. The initial goal is to explore in the heavy enzyme the dynamic timing of the oxygen compression mentioned above and to compare it to the light enzyme (isotopically unlabeled).

Figure 1.

Catalytic site of PNP. (A) Active site region showing the atomic geometry near the TS for PNP phosphorolysis with guanosine and phosphate. Guanosine is shown in gray; His257, Asn243, and Glu201 are shown in green; and phosphate is shown in orange. O_p is the nucleophilic oxygen from the phosphate. (B) Overlap of active site residues from the X-ray crystal structures of Native (green, PDB code 3PHB) and Glu258Asp Leu261Ala Mutant (cyan, PDB code 5ETJ) PNPs bound to the TS-analogue DADMeImmG. A stereoview version of (B) is shown in Figure S1.

RESULTS AND DISCUSSION

Coordinated Motions

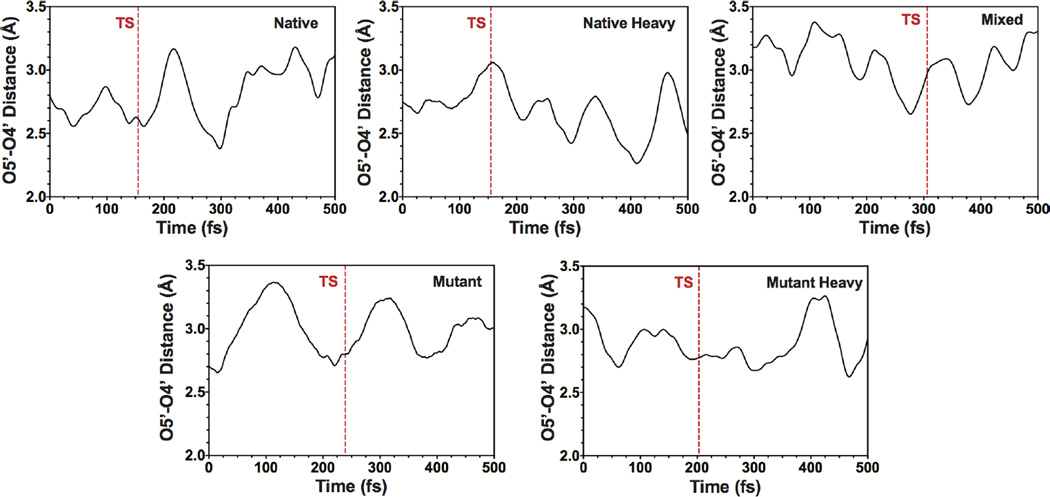
Transition path sampling (TPS) studies with PNP have shown that His257-linked compression of the ribosyl O5′–O4′ distance correlates with formation of the TS.^2,6,18 The reaction-promoting dynamics involving His257 are different between the native and heavy enzymes (Figure 2). Typical trajectories in native PNP have the compression of the O5′–O4′ distance coordinated with TS barrier crossing (as defined by the isocommittor surface, see below). This motion is known to favor TS formation. This coordination is less organized in the heavy enzyme, where the maximum compression often happens well after TS crossing.

Figure 2.

Representative trajectories showing the O4′–O5′ oxygen compression with respect to the TS for: Native PNP, Native Heavy PNP, Mixed PNP, Mutant PNP, and Mutant Heavy PNP. The vertical dashed line (red) shows the location of the TS. Note the coordination of O4′–O5′ oxygen compression with TS crossing in Native, which is absent in Native Heavy. This coordination is recovered in the mixed enzyme. Finally, the Mutant and Mutant Heavy enzymes are qualitatively similar. These are examples from all reactive trajectories, with distance and timing averages presented in Table 1.

Reaction Coordinate

We used TPS^19–22 and committor analysis to identify residues that are part of the reaction coordinate. First we generated 210 reactive trajectories for the native and heavy enzymes. Then we identified the isocommittor surface, defined as the set of configurations with the property that trajectories initiated from them have equal (50%) commitment probability to reach reactants or products. Once the isocommittor surface is known, because the reaction coordinate consists of the residues that remain in the same position along the isocommitor (TS) surface, these residues can be computationally identified by a committor analysis (see Experimental Materials and Methods): one iteratively searches for a set of residues that if held fixed while the rest of the protein is allowed to evolve in trajectories that are initiated from the isocommittor surface, then the constrained trajectories retain a commitment probability equal to 50%, that is, they end up in a TS structure. Initial input for which set of residues to constrain was suggested from previous work.⁷ The committor analysis confirmed that residues Asn243, Ser220, Glu201, Ser33, Tyr88, His86, and His257 are part of the reaction coordinate for native PNP, since they satisfied the requirement mentioned above that new restrained trajectories starting from the isocommitor surface lead to structures with committor distributions peaked at 0.5. In contrast, for the heavy enzyme, holding the same set of residues fixed in the committor test led to committor distributions whose peak shifted to 0.6, showing that the reaction coordinate in the heavy enzyme is different than in native PNP (Figure S2, panels 1–2).

Do Coordinated Motions Come from the Active Site or Global PNP Dynamics?

There are at least two distinct possibilities for the origin of the differences in TS barrier crossing in native and heavy enzymes: (a) they are dominated by local motions from residues in the active site of the heavy enzyme, or (b) that global changes in the protein structure affect TS crossing. To identify which circumstance exists, we computationally mutated the heavy enzyme by substituting the seven reaction-coordinate participating residues with light isotopes, while the rest of the enzyme remained isotopically labeled (termed “mixed” below and in Figure 2). We used TPS to generate 120 reactive trajectories, which were used in committor analysis, and the resulting isocommittor surfaces were the starting points for finding the reaction coordinate (Figure 2; Table 1). The reaction coordinate oxygen compression and timing with respect to the O5′–O4′ distance and TS formation are similar to the native PNP. In addition, the peak of the committor distribution for the native PNP reaction coordinate was shifted back to 0.5, meaning that the “mixed” enzyme has the same reaction coordinate as the native PNP. Therefore, the catalytic defect of the heavy enzyme has its origin in the mass-sensitive motion of the active site residues. The computational prediction of heavy PNP effects being local to the catalytic site has been confirmed experimentally. PNP with isotopically heavy His residues, including the three His at the catalytic site, showed significant reduction in TS formation.⁷

Table 1.

Minimal Values of the O5′–O4′ Distance Averaged over All Trajectories and Range of Time Separation from Minimum to TS Crossing

	distance (Å)	time range of point of minimal values from TS (fs)
native	2.53 ± 0.06	−17 to +3
heavy	2.62 ± 0.10	+36 to +68
mixed	2.66 ± 0.06	−15 to +8
light mutant	2.71 ± 0.08	−16 to +14
heavy mutant	2.76 ± 0.04	−16 to +17

Altering the Heavy Enzyme Effects

A major interest of the present work was to identify mutations for the heavy enzyme that specifically alter motions linked to TS formation for heavy and light PNPs. Because of the important role of His257 motion, we calculated the root-mean-square fluctuation (RMSF) of the C_α atom of the residue His257 averaged over all reactive trajectories. The results are 0.21 ± 0.04 Å for native PNP and 0.13 ± 0.02 Å for the heavy enzyme, showing that this residue is less mobile in the heavy enzyme. In an attempt to restore its flexibility, we mutated two residues that lie just behind it with respect to the catalytic site geometry (Figure S3). Conversion of Glu258 to Asp and Leu261 to Ala increased dynamic access behind His257 in the opposite direction from the active site, providing space for His257 to move more freely and to decrease the size (and mass) of the segment. In silico mutation of both the native and heavy enzymes (we denote them as “mutant” and “heavy-mutant” respectively), was followed by TPS to generate 150 reactive trajectories. The RMSF value for the heavy mutant is 0.17 ± 0.04 Å suggesting a more flexible His257 in the heavy mutant than in the heavy enzyme. We also plot RMSD vs time for a representative reactive trajectory for heavy and heavy mutant PNP, showing the difference in mobility for His257 in the heavy mutant (Figure S4). The averaged RMSD values for heavy PNP and heavy mutant are 0.18 ± 0.04 Å and 0.21 ± 0.05 Å, respectively.

A crucial result is that the calculations did not detect any significant differences in the structures of native compared to mutant enzymes (Figure S5). The calculated RMSD difference at the TS of the active site reactants, along with the seven reaction coordinate residues, is 0.47 ± 0.12 Å between native and mutant, and 0.68 ± 0.13 Å between heavy and heavy mutant. Experimental TS analysis of native and heavy PNP gave the same result, but the rate of barrier crossing was decreased.⁷

Coordination of the O5′–O4′ Compression with TS Crossing

Results for the mutant and heavy mutant PNPs show that in heavy mutant PNP, the mutations restore the dynamics of O5′–O4′ compression toward that of mutant PNP (Figure 2; Table 1). In other words, the heavy enzyme (mutant) now has geometric excursions more similar to light PNP. The mistiming with respect to TS crossing found in heavy PNP is altered in heavy mutant PNP. In addition, these mutations did not affect the native PNP reaction coordinate, leading to committor distributions peaked at 0.5 (Figure S2, panels 4–5).

Correlation of Structure with Dynamics

We examined the protein structure to determine if the overall structure or contacts to a TS analogue were changed by the mutations of Glu258Asp and Leu261Ala. The crystal structure of mutant PNP was solved in the presence of phosphate and DADMeImmG, a transition state analogue that binds with pM affinity. The structures are near-identical, including crystal packing (see Table S1). The α helix containing His257 and both mutations would be expected to be most sensitive to the mutations. However, the His257 to ribose distance is the same in native and mutant proteins (Figure 1B). Thus, the static structures are largely unchanged (trimer alignment between crystals structures 5ETJ and 3PHB gives an average RMSD of 0.52 Å; note each contain two trimers in the asymmetric unit), but TPS reveals that dynamic properties vary. An important TPS analysis correlation in the crystal structure of native PNP with DADMeImmG is the 2.6 Å distance between His257 and the 5′-OH group of ribose (compare Figure 1B and Table 2). This distance is unchanged in the crystal structure of mutant PNP, but analysis of the TPS trajectories shows an altered distance at the TS. The introduction of the Glu258Asp and Leu261Ala mutations do not significantly alter the static structure of PNP stabilized by DADMeImmG, except for the small change in His257 (Figure 1). This structure is near the TS as DADMeImmG is a TS analogue. However, the Glu258Asp and Leu261Ala mutations do alter the O5′–O4′ distance at the TS as determined from TPS, as does the heavy PNP compared to native PNP (Table 2).

Table 2.

Distances O5′–O4′ (Å) during the TS Crossing

	distance O5′–O4′ 10 fs before TS	distance O5′–O4′ at the TS
native	2.57 ± 0.04	2.56 ± 0.07
heavy	2.93 ± 0.05	2.94 ± 0.06
light mutant	2.81 ± 0.06	2.78 ± 0.08
heavy mutant	2.81 ± 0.07	2.82 ± 0.06

Effects of Glu258Asp Leu261Ala Mutations on PNP Kinetics

We examined how the Glu258Asp and Leu261Ala mutations affect the steady state kinetic constants (k_cat and K_M), the chemical rate at the catalytic site (k_chem), and the affinity of the transition state analogue DADMeImmG, the TS mimic studied in the crystallographic analysis.

Native, heavy, mutant (Glu258Asp/Leu261Ala), and heavy mutant PNPs were expressed and purified to homogeneity as indicated in the Methods. The mass differences determined by MALDI-TOF-MS between the labeled and unlabeled proteins were >10%, indicating efficient ¹³C, ¹⁵N, and ²H incorporation into heavy enzymes. Deuterium substitution is limited to nonexchangeable positions, as solvent exchangeable positions exchange during purification and storage. Light and heavy native PNPs and mutant and heavy mutant PNPs gave similar Michaelis–Menten kinetic parameters and k_cat/K_M constants for the phosphorolysis of guanosine, consistent with previous reports.⁷ The steady-state rate of guanosine phosphorolysis k_cat for the mutant enzymes was reduced by ~50% (see Table 3). As the rate-limiting step in PNP catalysis is the release of the guanine product, the steady-state rates indicate that the mutations introduce a small change in the slow conformational changes associated with product release. Our focus is on the rate of chemistry on the enzyme, independent of the product release rates.

Table 3.

Kinetic Constants for Native and Mutant PNPs

	kcat (s−1)	KM (µM)	kcat/KM (M−1 s−1)	kchem (s−1)	on-enzyme KIE
native (light)	8.8 ± 0.5	63 ± 8	1.4 × 105 ± 0.2	157 ± 6.04
native (heavy)	8.0 ± 0.3	54 ± 4	1.5 × 105 ± 0.1	130 ± 3.4	1.21 ± 0.06
mutant (light)	4.2 ± 0.4	73 ± 13	5.8 × 104 ± 1.1	1.57 ± 0.01
mutant (heavy)	4.2 ± 0.2	64 ± 9	6.6 × 104 ± 1.0	1.58 ± 0.01	0.997 ± 0.005

Catalytic Site Chemistry Rates

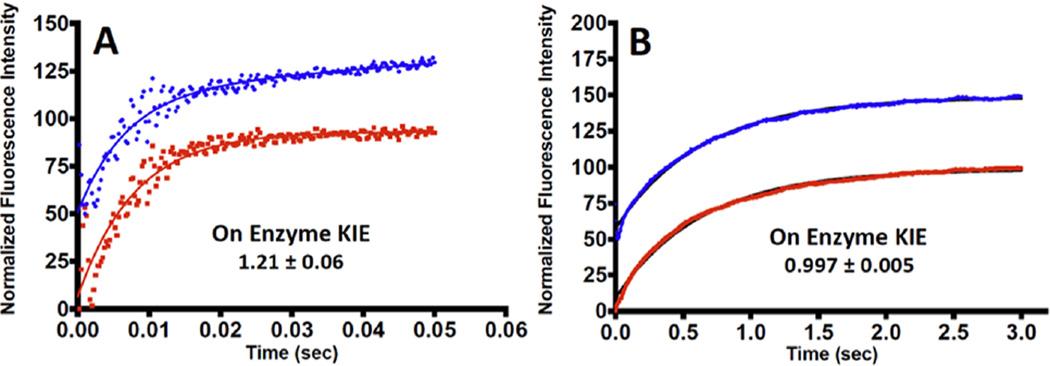
Presteady-state single turnover rate constants were measured for light and heavy PNPs for the phosphorolysis of guanosine. The enzyme was used in molar excess relative to guanosine to give first-order rate constants, independent of enzyme concentration. The catalytic site chemical rate constant (k_chem) was reduced by a factor of 100 in mutant PNP (Table 3; Figure 3). Considering the relatively small 2-fold change in k_cat, the conclusion is that the second-sphere mutations have a more profound effect on TS barrier crossing than on the conformational changes associated with product release. Since little catalytic site difference is seen in X-ray structural analysis for the mutant enzyme, dynamic contributions to catalysis are implicated. Heavy enzyme KIE values were based on the catalytic single turnover rate constants (light k_chem/heavy k_chem) obtained in stopped flow studies. The observed KIEs for the labeled enzymes were 1.21 ± 0.06 for native PNPs and 0.997 ± 0.005 for mutant PNPs (Figure 3). The chemical rate of reaction catalyzed by PNP is sensitive to mass as reported earlier, and confirmed here. Altered mass of amino acids changes the local probability of arranging all of the amino acids to the transition state configuration in the proper time sequence. One manifestation of that change is the O5′–O4′ distance either before or at the TS (Table 2). For native and heavy PNP, increased enzyme mass changes this ribocation-assisting distance from 2.6 to 2.9 Å before or at the transition state. This decreased promoting interaction may contribute to the slowed chemistry observed with heavy PNP. It should be noted that the heavy enzyme does achieve full compression of O5′–O4′ in all reactive trajectories, but at a later point in the reaction coordinate. On the other hand, with mutations of Glu258Asp and Leu261Ala, the O5′–O4′ distance before and at the transition state increases relative to native PNP, from 2.6 to 2.8 Å. The mutations have a larger effect on the rate of TS formation than the mass substitution. However, with heavy and light mutant PNPs, the distances 10 fs before and at the TS are equivalent, and this is manifested in the loss of the heavy-enzyme effect compared to the mutant enzyme (Table 3).

Figure 3.

Representative single turnover experiments for guanosine phosphorolysis for Native and Mutant PNP with light and heavy isotopes. (A) Native Light (blue trace), Native Heavy (red trace). (B) Mutant Light (blue trace), Mutant Heavy (red trace). The kinetic traces are offset on the ordinate scale for presentation purposes. Kinetic traces in (A) were fit to double exponentials, where only the fast phase reports on the chemistry step (k_chem) reported in Table 3. The slower reaction rates in (B) were fit to a single exponential representing the chemistry step reported in Table 3.

Glu258Asp Leu261Ala Mutations on PNP Interactions with DADMe-ImmG

DADMeImmG is a slow-onset, tight binding transition state analogue inhibitor of native PNP. Under the conditions used here, the initial dissociation constant (K_i) for PNP-DADMeImmG interaction is 216 ± 13 pM followed by a slow-onset tightening of the inhibition to give an equilibrium dissociation constant changes (K_i*) of 15 ± 2 pM. Slow-onset tight binding inhibition is attributed to conformational changes of the protein to accommodate the geometry of the TS analogue without the catalytic step as occurs in the normal reaction.¹² As the TS analogue is an imperfect mimic of the TS, the tight-binding conformational changes are slow relative to the catalytic rate. With the double mutant Glu258Asp and Leu261Ala PNP, the initial affinity is tighter, a dissociation constant of 85 ± 7 pM and there is little slow-onset change, to give a final K_d of 66 ± 2 pM. The altered second sphere amino acids are proposed to relax the conformational geometry to permit TS analogues to bind near-optimally without a slow-onset phase. Instead, the protein rapidly attains its equilibrium affinity for the inhibitor, albeit with a 4-fold weaker binding of the inhibitor for the mutant PNP.

Summary

This is the first study incorporating computational and experimental results exploring mutations capable to reversing the mass alteration effect on enzymatic chemical turnover rates. Earlier work had shown that the perturbation induced by heavy isotopic replacement alters the dynamics in the active site, making it less probable for critical dynamic events to coordinate. We focused on His257 motion, known to cause the compression of oxygens from phosphate, ribose-O4′, and ribose-O5′ (the 3-oxygen stack), which in turn is linked to His257 motion and TS formation. The mutation of two second layer residues in the vicinity of His257 is proposed to increase its vibrational freedom and result altered timing of the promoting vibration linked to barrier crossing. Thus, the contribution of His257 dynamics in mutant and heavy mutant PNPs is similar, despite the mutations changing the rate of TS formation on the enzyme and the decreased binding of a TS analogue. In other words, the mutants restored one aspect of dynamics which is the timing of the compression, but loss of the fast vibrational coupling between His257 to TS formation decreased the oxygen compression which in turn decreased the chemical rate by 2 orders of magnitude. This analysis of the His257 region of the PNP catalytic site is only one dimension of the catalytic interactions that also activate the leaving group purine and the phosphate nucleophile. They are susceptible to similar exploration to obtain a better picture of dynamic contributions to catalysis. These ideas can be viewed as the first few steps in a program that it will eventually include rapid protein dynamics as part of a design paradigm.

COMPUTATIONAL METHODS

All simulations were performed using the CHARMM^23,24 molecular dynamics package. The starting point for the simulations was crystal structure 1RR6 from the Protein Data Bank. It is a homotrimeric human PNP structure in complex with Immucillin-H and phosphate. This starting point yields barrier crossings with TPS (see below), and is therefore considered to be on the reaction coordinate path. To build our model, the transition state inhibitor (Immucillin-H) was modified to the guanosine substrate by replacing atoms N4 with O4 and C9 with N9. His257 was modeled as the neutral form with a proton at NE leaving ND1 to interact with 5′-hydroxyl of the ribose ring.²⁵ The catalytic site residue Glu201 was deprotonated at neutral pH to stabilize the purine base. Atom N7 of the purine base was protonated because transition state analysis¹⁷ has established N7 protonation to N7H before reaching the transition state. For the heavy PNP enzymes, we manually modified the atomic masses of C, N, and nonexchangeable H of the amino acids with heavy isotopes. The structure has 13 275 atoms, 75 crystallographic water molecules, and 3 HPO₄²⁻ molecules. All crystallographic waters were retained. The mutated structure has 13 263 atoms. Simulations for native and heavy PNPs and their mutated versions, were performed separately following the same protocol.

The system was partitioned into quantum and molecular mechanics regions where the QM region consisted of 40 atoms including the protonated N-guanosine and HPO₄²⁻ moieties and was modeled using the PM3 semiempirical method due to the presence of the reactive phosphate group.²⁶ The remaining atoms of the protein, ions, and solvent water molecules were in the MM region. There were no covalent bonds between the atoms of the QM and the MM regions.

The protein was solvated in a sphere of waters of 60 Å radius, using explicit TIP3 water molecules. During solvation 25173 water molecules were added. Then, the system was neutralized by placing 18 chloride and 29 sodium ions. The system was minimized using 150 steps of steepest descent (SD) followed by 6000 steps of adopted basis Newton–Raphson (ABNR) minimization. The heating was conducted slowly from 0 to 300 K for 70 ps while any harmonic constraints applied to the system were gradually released. During the last 10 ps we switched the QM/MM on. After the heating phase, the system was equilibrated at 300 K with the QM/MM on for 150 ps.

TPS^19–22 was used to analyze the structure of reactive trajectories, following these steps. First, the order parameters were defined by the C1′–N9 bond-breaking and C1′–O_p bond-forming distances, such that the reactant region contains all configurations with the C1′–N9 bond length < 1.7 Å and the C11–O_p bond length > 1.65 Å, while the product region contains all configurations with C1′–N9 bond length > 1.7 Å and C1′–O_p bond length < 1.65 Å. Then we perturbed the momenta of a randomly chosen slice of this reactive trajectory and propagated using the new momenta until we generated a new reactive trajectory. We repeated this process until a sufficient set of reactive trajectories had been generated. Next, we performed committor analysis, where one identifies the time slice with the property that new trajectories starting from that slice have probability 0.5 to reach reactants or products. These isocommittor structures are the transition state ensemble (TSE). The TPS method can generate the TSE without any knowledge of the reaction coordinate.

The TPS iteration needs an initial reactive trajectory, which was generated by applying a harmonic force with constant 65 (kcal/mol)/Ų on both the bond-breaking and bond-forming distances and propagated for 250 fs. Using the initial biased trajectory as seed for the TPS iteration, we generated 210 and 150 reactive trajectories of 500 fs for the native and mutated PNPs respectively, and 120 trajectories for the “mixed” PNP enzyme. From the harvested reactive trajectories we identified a TSE of 25 uncorrelated transition state structures for the native and heavy enzymes, and 15 uncorrelated transition state structures for the “mixed” enzyme and light and heavy mutants.

The next step was the reaction coordinate identification.²⁷ Residues that define the TS remain in the same relative position along the isocommittor surface, while the TS does not depend on the position of the rest of the residues. This property suggests a computational algorithm for identifying the reaction coordinate. One starts with structures on the isocommittor surface and makes a guess for the reaction coordinate residues. One then initiates new trajectories from the isocommitor surface, constraining the residues of the guess for the reaction coordinate but allowing the rest of the system to move. If those residues are indeed part of the reaction coordinate, from the definition of the isocommittor surface, the structure at the end of the constrained trajectory will have remained on the isocommittor surface; that is, the commitment probabilities should be 0.5 for reaching reactants or products. If the guess for the reaction coordinate residues fails, we make a new guess and iterate until the isocommitor test succeeds. We used four uncorrelated transition states as starting points for this procedure.

It should be noted that an alternative computational method, that has similar content as TPS analysis, is the variational transition state theory combined with calculation of the recrossing coefficient.^4,28

EXPERIMENTAL MATERIALS AND METHODS

Materials

99.8% Deuterium oxide (D₂O), [U-¹³C6, 1, 2, 3, 4, 5, 6 6-²H₇]glucose, and [¹⁵N]ammonium chloride were purchased from Cambridge Isotopes Laboratories, Inc.

Site Directed Mutagenesis

Mutagenesis was performed using the Q5-site directed mutagenesis kit from New England Biolabs. DNA primers (Invitrogen) were designed to introduce the two second shell mutations Glu258Asp and Leu261Ala. The sequences of the oligonucletide pair (mutated codons are in boldface) were as follows: Forward, 5′-TGACGAAGTCGCAGCAGCTGGCAAAC-3′; reverse, 5′-TGGTTGGCCTTCTCCAGG-3′. Mutagenesis was performed in accordance with the manufacturer’s protocol, and the reaction product was transformed into the Escherichia coli BL21(DE3) pLysS (invitrogen) strain for selection and expression purposes. The presence of the mutated codons was confirmed by DNA sequencing.

Production of Natural Abundance and [²H ¹⁵N ¹³C] PNP

Native and double mutant (E258D/L261A) PNP were expressed in E. coli BL21(DE3) cells harboring a pCR-T7/NT-TOPO vector (Invitrogen) containing the encoding sequence for human PNP. Heavy PNPs were expressed in E. coli BL21(DE3) pLysS (Invitrogen) cells, containing the same construct. [²H ¹⁵N ¹³C]PNP was expressed in cells grown in M63 minimum medium prepared in 99.8% deuterium oxide (D₂O) supplemented with [U-¹³C₆, 1, 2, 3, 4, 5, 6 6-²H₇]glucose (3 g/L) and [¹⁵N]ammonium chloride (1 g/L), containing 100 µg/mL ampicillin, at 37 °C. After OD₆₀₀ = 1.0 was reached, protein expression was induced by addition of 1 mM isopropyl-1-thio-β-d-galactopyranoside. Cells were allowed to grow for additional 24 h and harvested by centrifugation. Both light and heavy PNPs were purified by Ni-NTA affinity chromatography. Protein concentration was determined spectrophotometrically at 280 nm using the predicted extinction coefficient of 29 910 M⁻¹ cm⁻¹ (http://expasy.org). Subunit molecular mass was determined by MALDI-TOF-MS.

Steady-State Kinetic Analysis

Steady-state kinetic parameters were determined by measuring initial reaction rates as a function of guanosine or inosine concentration at 25 °C. The decrease in absorbance at 258 nm upon conversion of guanosine to guanine (Δε = −5500 M⁻¹ cm⁻¹) was monitored in a Cary 100 spectrophotometer (Varian). Guanosine phosphorolysis reactions contained 50 mM Tris-HCl pH 7.4, 50 mM potassium phosphate pH 7.4, varying guanosine concentrations (10–160 µM), and 20 nM of light or heavy PNPs. Kinetic parameters were obtained by data fitting to eq 1, where ν is the initial velocity, V is the maximal velocity, S is the concentration of variable substrate, and K_M is the Michaelis constant for the variable substrate.

$$\nu =(VS)/(S+K_{\mathrm{M}})$$ (1)

Inhibition Assays

Activity assays for native and mutant PNP enzymes with inosine as a substrate were performed by monitoring the conversion of hypoxanthine to uric acid (ε₂₉₃ = 12 900 M⁻¹ cm⁻¹) in a coupled assay containing 60 milliunits of xanthine oxidase and variable concentrations of inosine, in 50 mM phosphate buffer pH 7.4 at 25 °C.¹⁷ The slow onset inhibition kinetics were measured following the addition of enzyme to complete assay mixtures containing 1 mM inosine and various inhibitor concentrations.^15,17 The rates of product formation were monitored for 1–2 h to determine the initial reaction rates and to determine if slow onset inhibition occurred. Initial reaction rates and final reaction rates after equilibration for slow-onset were fit to the equations for tight-binding inhibitors.^10,29 The initial inhibition is given by K_i and the equilibrated slow-onset value given by K_i*. Protein and inhibitor concentrations were determined by their corresponding extinction coefficients.

Pre-Steady-State Kinetic Analysis

Single-turnover on-enzyme rate constants were determined by monitoring the increase in fluorescence upon formation of enzyme-bound guanine in an SX-20 stopped-flow spectrofluorometer (Applied Photophysics; dead time ≤ 1.25 ms) at 25 °C. The excitation wavelength was 280 nm with slit width of 1 mm, and a fluorescence signal above 305 nm (with slit width of 1 mm) was selected using a WG305 Scott filter positioned between the photomultiplier and the sample cell. Fluorescence change was monitored for 250 ms, and 1000 points were collected for each individual rate curve. Syringe 1 contained 50 mM Tris-HCl pH 7.4, 50 mM potassium phosphate, pH 7.4, and either light or heavy PNP at 30 µM (15 µM postmixing concentration). Syringe 2 contained 50 mM Tris-HCl pH 7.5, 50 mM Pi, pH 7.4, and 10 µM guanosine (5 µM postmixing concentration).

Crystallization of PNP (E258D, L261A) with DADMe-Immucillin-G

The enzyme was concentrated to 10 mg/mL and incubated with 2 equiv of DADMe-Immucillin-G (DADMeImmG). The protein was crystallized with the N-terminal His6/Xpress tag intact at 22 °C using the sitting drop vapor diffusion technique. Block-shaped crystals (50 µm × 90 µm × 90 µm) were obtained over 3 weeks using 0.2 M lithium sulfate, 0.1 M TRIS-HCl (pH 8.5), and 20% (w/v) polyethylene glycol 4000.

Data Collection and Processing

The inhibitor-bound PNP (double mutant) crystals were transferred to a cryoprotectant solution containing 20% (v/v) glycerol and the respective mother liquors [80% (v/v)] prior to being flash-cooled in liquid nitrogen. Diffraction data for PNPdbl·DADMeImmG crystals were collected with 0.9793 Å wavelength radiation at the LRL-CAT beamline (Argonne National Laboratory, Argonne, IL) on a Rayonix 225 HE CCD detector to 2.30 Å resolution. Diffraction intensities were integrated and scaled with XDS.³⁰ The diffraction data statistics are summarized in Table S1.

Structure Determination

The structure of PNPdbl·DADMeImmG (PDB ID: 5ETJ) was determined by molecular replacement with Molrep,³¹ using a single monomer from the previously published structures of PNP· DADMeImmG (PDB entry 3PHB) as a search model. The refinement of the initial solution and subsequent refinements were conducted using a restrained refinement performed with Refmac,³² using all data between 25.0 and 2.3 Å. Manual model rebuilding was conducted using Coot.³³ Difference Fourier maps calculated with F_obs − F_calc coefficients revealed ordered water and phosphate molecules and strong unambiguous density difference, corresponding to the DADMeImmG inhibitor. The mmCIF component definition file for the inhibitor was downloaded from the PDB, having the monomer code IM5. Water molecules with proper hydrogen bonding coordination and electron densities greater than 1 RMSD and 3 RSMDs in maps calculated with 2F_obs − F_calc and F_obs − F_calc coefficients, respectively, were included in the model. For each of the monomers in this structure, all but the last three residues of the PNP_dbl sequence (residues 1–286) and one or two of the 35 residues in the His6 tag were sufficiently ordered to be included in the model. This structure was refined to an R_cryst of 17.8% and an R_free of 21.1%. Analysis of the structures in Coot revealed good stereochemistry with only Thr221 of each monomer falling into the disallowed region of the Ramachandran plot. The refinement statistics are listed in Table S1.