Mathematical Model of Oxygen Transport in Tuberculosis Granulomas

Abstract

Pulmonary granulomas—the hallmark of Mycobacterium tuberculosis (MTB) infection—are dense cellular lesions that often feature regions of hypoxia and necrosis, partially due to limited transport of oxygen. Low oxygen in granulomas can impair the host immune response, while MTB are able to adapt and persist in hypoxic environments. Here, we used a physiologically based mathematical model of oxygen diffusion and consumption to calculate oxygen profiles within the granuloma, assuming Michaelis–Menten kinetics. An approximate analytical solution—using a priori and newly estimated parameters from experimental data in a rabbit model of tuberculosis—was able to predict the size of hypoxic and necrotic regions in agreement with experimental results from the animal model. Such quantitative understanding of transport limitations can inform future tuberculosis therapeutic strategies that may include adjunct host-directed therapies that facilitate oxygen and drug delivery for more effective treatment.

INTRODUCTION

As one of the most virulent infectious diseases in the world today, tuberculosis (TB) accounts for almost 2 million deaths and 2 billion latent infections annually.¹⁵ While current treatment regimens are largely successful in curing the infection, multi-drug resistant Mycobacterium tuberculosis (MTB) strains have proliferated, in part due to poor adherence to the 6-month duration of standard treatment.^42,56 Clearly, a better understanding of the physiochemical characteristics of tuberculosis pathology and progression would help in the development of more effective treatment protocols. TB progression—and, inevitably, treatment response—is governed by the formation and evolution of pulmonary granulomas, the primary sites of infection.

TB granulomas are dense cellular masses, comprised primarily of immune cells, that form in the lungs in response to MTB infection.^16,36 Some granulomas recruit new blood vessels in the peripheral regions of the tissue mass that abut the healthy lung tissue.^34,41 These angiogenic vessels presumably allow granulomas to grow to sizes that exceed the diffusion distance of oxygen (<200 μm from a vessel^8,46). Tuberculosis granulomas typically contain hypoxic regions⁴⁸ resulting in altered MTB metabolism.^38,39 These hypoxic areas often surround necrotic cores (Fig. 1), which are regions comprised of lipid-rich, cellular debris.^13,37

FIGURE 1.

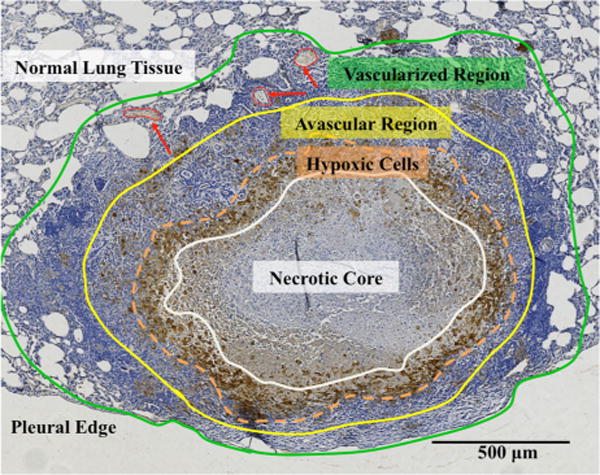
TB granuloma regions can be delineated based on vasculature and local oxygen concentration. In the immunohistochemical (IHC) image of a rabbit granuloma stained with pimonidazole for hypoxia, the four stratified layers described in the model are shown with colored borders (where red arrows indicate some blood vessels): (1) a necrotic core (white), (2) a region with hypoxic cells (orange), (3) an avascular region where cells are not hypoxic but blood vessels do not exist (yellow), and (4) an outer vascularized region where blood vessels are present (green, red arrows).

MTB has been shown to be responsive to changes in oxygen tension; indeed, many in vivo and in vitro models have demonstrated that bacterial growth, metabolic activity, and transcriptional profiles are altered by hypoxia.^25,28,38,40 Some mycobacteria are able to shift to a dormant phenotype of “bacteriostasis,” or non- or slow-replication, that can persist for years.^5,39,49–51 Furthermore, some bacilli undergo transcriptional adaptations that reduce drug susceptibility in hypoxic conditions.^27,50 This suggests a prominent role of oxygen in the latency and reactivation of the TB bacilli. Additionally, we have recently shown that granulomas are associated with abnormal vasculature, thus compromising the effective delivery of oxygen and TB drugs.¹¹

Interestingly, a very different disease that evolves in a similar manner is cancer, in that it also produces dense tissue masses, i.e., tumors, with abnormal vasculature and resulting regions of hypoxia and necrosis. The physiological abnormalities that characterize solid cancerous tumors have, in fact, been investigated thoroughly²³; it is now well known that these unique properties—most notably, irregular, spatially and temporally heterogeneous vascular networks—compromise the delivery of oxygen, nutrients, drugs and immune cells within the tumor tissue.^8,20–22 Furthermore, hypoxia is known to drive immunosuppression in tumors ²⁴; this may occur in the hypoxic granuloma regions, although this has yet to be confirmed.

The physiological similarities between solid tumors and TB granulomas motivate a quantitative understanding of the underlying transport limitations within granulomas. To this end, the present work describes the limits of oxygen transport within TB granulomas via a mathmatical modeling approach originally applied to tumors. Oncology has long benefitted from the use of these models to illuminate biological processes associated with tumor progression. While these models can become rather complex, especially when describing dynamic processes such as angiogenesis,^31,44 simpler mathematical models of avascular tumors can reveal highly relevant insight about early, macro-scale mechanisms of tumor growth.^2,35 In particular, heterogeneous avascular models are used to describe stratified layers of a tumor mass—such as non-necrotic vs. necrotic regions—based on oxygen distribution.^26,35 Deakin¹² was the first to develop an analytical model for the emergence of necrotic cores in tumor spheroids based on the assumption that the oxygen consumption in avascular tumors is constant, or zero-order, with respect to oxygen concentration, until the concentration decreases due to cellular consumption to a low value, below which the consumption is first-order, i.e., proportional to the concentration.¹² As the oxygen concentration decreases further, a critical concentration is reached at which cells die and necrosis occurs. These assumptions of oxygen concentration match the so-called Michaelis–Menten (MM) mitochondrial oxygen consumption kinetics,^{7,10,29,52,53} employed in later biological⁴³ and avascular tumor models.^19,26

Here we developed a theoretical model of oxygen diffusion and consumption, based on the rich avascular tumor model literature, for TB granulomas. Previously reported and newly collected experimental data provide relevant parameters for the model. Model predictions of hypoxia and necrosis are in concert with experimental results from a rabbit model of TB. Moreover, this model serves to provide a conceptual framework within which the experimental observations can be quantitatively interpreted, and represents the first step toward understanding and eventually overcoming the transport limitations within TB granulomas.

MATERIALS AND METHODS

The parameter values used in this model can be found in Table 1. The basic formulation steps and assumptions of the model are given below. To make our work accessible to a broad readership, the detailed derivation and justification of parameter values are provided in the Supporting Material.

TABLE 1.

Parameter values for the mathematical model of oxygen transport in rabbit TB granulomas, determined as described in the Supporting Material.

Parameter	Value	Units	References
$H_{{\mathrm{O}}_2}$	1.34 × 10−9	mol O2/cm3–mmHg	47
$D_{{\mathrm{O}}_2}^e$	2.5 × 10−5	cm2/s	Adapted from 9, 18, 47
$P_{{\mathrm{O}}_2,b}$	60	mmHg	48
$P_{{\mathrm{O}}_2,H}$	10	mmHg	3, 14, 32
$P_{{\mathrm{O}}_2,C}$	2	mmHg	48
$C_{{\mathrm{O}}_2,b}$	8.04 × 10−8	mol O2/cm3	From Henry’s law $C_{{\mathrm{O}}_2}=H_{{\mathrm{O}}_2}{p}_{{\mathrm{O}}_2}$
$C_{{\mathrm{O}}_2,H}$	1.34 × 10−8	mol O2/cm3	From Henry’s law $C_{{\mathrm{O}}_2}=H_{{\mathrm{O}}_2}{p}_{{\mathrm{O}}_2}$
$C_{{\mathrm{O}}_2,C}$	2.68 × 10−9	mol O2/cm3	From Henry’s law $C_{{\mathrm{O}}_2}=H_{{\mathrm{O}}_2}{p}_{{\mathrm{O}}_2}$
k	1.09	s−1	From Eqs. (18) and (19)
K	7.46 × 107	cm3/mol O2	From Eq. (20)

Model Formulation and Assumptions

Figure 1 shows the stratification of cellular/vascular layers based on oxygen availability in a representative TB granuloma. From this morphology, four distinct areas can be described: (1) a necrotic core surrounded by (2) a region where cells are hypoxic, (3) a region where cells are not hypoxic although blood vessels do not exist, and (4) an outer non-hypoxic region where blood vessels exist (“vascularized region”). The tissue area between the regions where vessels exist and the necrotic core, i.e., the region between the yellow and white demarcations in Fig. 1, represents the “avascular region,” where oxygen is delivered by diffusion only.

In the idealized schematic in Fig. 2, the granuloma is considered as a spherical particle. Figure 2a denotes four radii of interest (measured experimentally via image analysis methods described in the Supporting Material): (1) the outer granuloma radius, R₀, (2) the radius of the avascular region, R, (3) the radius of the hypoxic region, R_H (indicated experimentally by positive pimonidazole stain, as described in the Supporting Material), and (4) the radius of the necrotic core, R_C (indicated experimentally by the presence of cellular debris and lack of viable cells). The regions and radii depicted in Fig. 2a have corresponding oxygen concentrations, $C_{{\mathrm{O}}_2}$, and oxygen consumption rates, $Q_{{\mathrm{O}}_2}$, shown schematically in Fig. 2b. It is assumed that the perfused (i.e., vascularized) region (R₀ to R) has a uniform bulk concentration of oxygen ( $C_{{\mathrm{O}}_{2,}b}$), resulting from an adequate supply of oxygen from the local vasculature. Starting at the boundary of the avascular region (r = R) and moving towards the granuloma center, the oxygen concentration decreases (from $C_{{\mathrm{O}}_{2,}b}$) with distance into the granuloma interior due to cellular consumption until it reaches a concentration at which cells become hypoxic ( $C_{{\mathrm{O}}_{2,}H}$), as indicated by positive pimonidazole staining (Fig. 1), at granuloma radius r = R_H. Within the hypoxic region (r < R_H), the oxygen concentration decreases further from $C_{{\mathrm{O}}_{2,}H}$ until it reaches a critical oxygen concentration ( $C_{{\mathrm{O}}_{2,}C}$)^12,26 at which cells die, i.e., necrosis sets in, at a granuloma radius, r < R_C. Throughout the necrotic core (r < R_C) the oxygen concentration remains at a constant value of $C_{{\mathrm{O}}_{2,}C}$, because there is no longer any cellular consumption of oxygen (i.e., $Q_{{\mathrm{O}}_2}=0$). The respective oxygen concentrations are defined numerically as model parameters in the Supporting Material.

FIGURE 2.

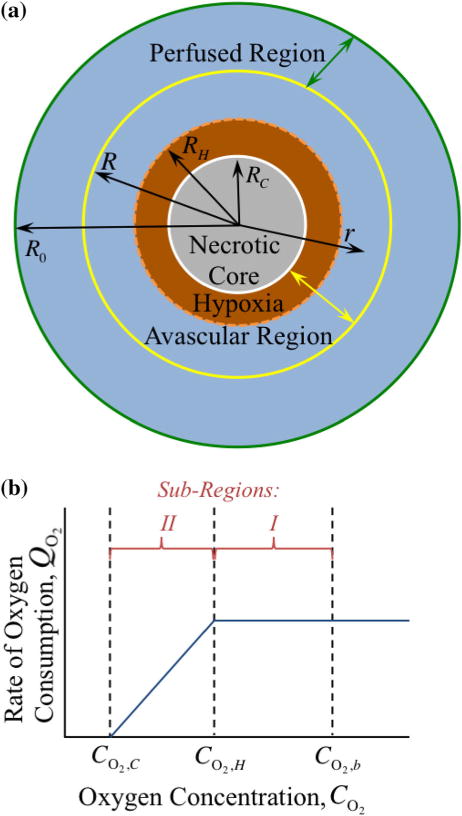
The stratified layers of oxygen transport, based on the presence of blood vessels as described in the model assumptions and Fig. 1, are shown with the four radii of interest (a). Non-uniform oxygen consumption, $Q_{{\mathrm{O}}_2}$, is shown as a function of oxygen concentration, $C_{{\mathrm{O}}_2}$ (b). The perfused region contains a constant bulk concentration of oxygen, $C_{{\mathrm{O}}_2,b}$, due to adequate supply from the local vasculature. At the boundary of the avascular region R, in which no blood vessels exist, the concentration of oxygen, $C_{{\mathrm{O}}_2}=C_{{\mathrm{O}}_2,b}$. The oxygen concentration drops with distance into the granuloma interior due to cellular consumption $C_{{\mathrm{O}}_2,b}$ to $C_{{\mathrm{O}}_2,H}$ (at some unknown value of granuloma radius r = R_H), where the cells become hypoxic. The oxygen concentration continues to drop further to $C_{{\mathrm{O}}_2}=C_{{\mathrm{O}}_2,C}$ (at some unknown value of granuloma radius r = R_C), at which point the cells die and necrosis emerges; thus, the consumption rate of oxygen becomes zero here, so the oxygen concentration remains constant at $C_{{\mathrm{O}}_2,C}$. The area between the avascular and hypoxic radii is defined as sub-region I (non-hypoxic), while the area between the hypoxic and necrotic radii is defined as sub-region II (hypoxic); it is assumed that the local oxygen availability results in zero- and first-order oxygen consumption kinetics in sub-regions I and II, respectively.

As described in the Supporting Material, the experimental data used to determine parameter values and to make comparisons to the mathematical model predictions come from granulomas at a state of disease progression where the granuloma size is essentially static, i.e., the macroscopic growth rate of these lesions can be considered zero. Therefore, oxygen transport in an idealized avascular granuloma can be written as a one-dimensional mass balance equation (see Eqs. (1) and (2) in the Supporting Material for details) as

$$\begin{array}{ccc}\underset{\text{Diffusion of Oxygen}}{\underbrace{D_{{\mathrm{O}}_2}^e\frac{1}{r^2}\frac{d}{\mathit{dr}}\left(r^2\frac{d{C}_{{\mathrm{O}}_2}}{\mathit{dr}}\right)}}& -& \underset{\text{Cellur Consumption of Oxygen}}{\underbrace{\frac{k{C}_{{\mathrm{O}}_2}}{1+K{C}_{{\mathrm{O}}_2}}}}\end{array}=0$$

where the first term on the left hand side describes the transport of oxygen in the granuloma tissue via diffusion and the second term on the left hand side is the Michaelis–Menten (MM) kinetic relation for oxygen consumption. The zero on the right hand side follows from the steady-state assumption, i.e., there is no accumulation of oxygen in the granuloma. Here, it is apparent that each term in the oxygen mass balance above is dependent on specific parameters; (1) the diffusion of oxygen is dependent on the effective diffusivity of oxygen in the granuloma interstitium ( $D_{{\mathrm{O}}_2}^e$), and (2) the MM kinetic relation is dependent on two kinetic parameters (k and K).

In addition to the assumptions of specific oxygen concentrations at corresponding radii, we also assume that the flux of oxygen across these defined boundaries is continuous. Regarding the oxygen consumption term, the MM equation is considered to be adequate for describing the observed hyperbolic dependence of consumption rate on oxygen concentration.^6,55 It does not, however, represent the true complexity of the mitochondrial processes regulating oxygen consumption. For instance, it does not reflect the fact that below a critical oxygen concentration the metabolic machinery shuts down resulting in cellular necrosis¹⁸; therefore, we include a boundary condition that satisfies this physical reality. Furthermore, MM kinetics can be reduced to limiting forms,⁴⁷ based on the dependence of oxygen consumption on oxygen concentration. It is assumed here that the differential availability of oxygen in the hypoxic and non-hypoxic regions of the avascular region results in zero-order and first-order oxygen consumption kinetics in sub-regions I and II, respectively (Fig. 2b). Finally, we assume that the MTB within the granuloma core respire anaerobically, based on known adaptations to low oxygen conditions.

Thus, the physics of oxygen diffusion and consumption as described above are formulated mathematically for the TB granulomas as a system of ordinary differential equations in the Supporting Material, using a one-dimensional model with these boundary conditions.

Model Parameters

With the appropriate parameters, the radii of the necrotic and hypoxic regions, R_C and R_H, can be determined from the above mathematical model, and compared to experimental data from the rabbit model of TB. Clearly, the model predictions depend upon the reliability of the model parameters. In this study, all parameters, except for two physical parameters—k, the first-order rate constant from the MM kinetic expression for oxygen consumption, and $D_{{\mathrm{O}}_2}^e$, the effective diffusivity of oxygen in the granuloma interstitium (see the Supporting Material for further descriptions)—are determined from either a priori⁴⁸ or new measurements from the rabbit experimental model. The justification for the choice of model parameters is given in the Supporting Material and the parameter values are summarized in Table 1.

Animal Experiments and Image Analysis

Untreated control tissues from a previously published experiment in the rabbit TB model¹¹ were used to assess the hypoxic and necrotic radii in rabbit granulomas via histological image analysis for comparison to the model predictions (for details see the Supporting Material).

RESULTS

Based on the theoretical model assumptions and formulation above and in the Supporting Material, a system of nonlinear ordinary differential equations was developed here to describe oxygen transport in an idealized spherical TB granuloma. For ease of presentation, dimensionless variables are used to describe granuloma size and various radii (e.g., hypoxic and necrotic radii), MM kinetics, and oxygen concentration profiles in Figs. 3, 4, 5, and 6.

FIGURE 3.

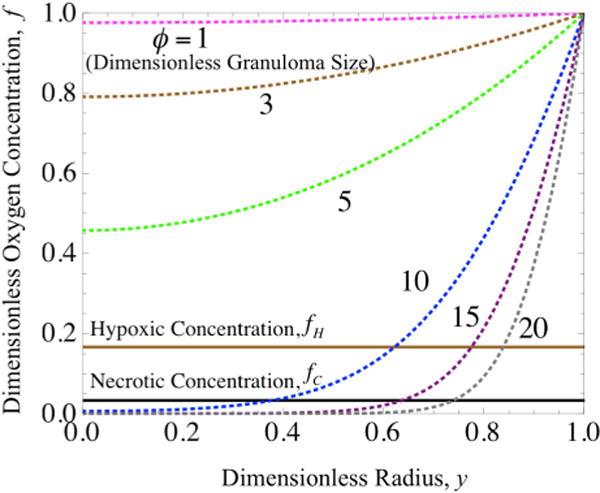
Oxygen concentration profiles modeled assuming Michaelis–Menten kinetics (dashed lines) and plotted for varying values of granuloma radius (ϕ) vs. oxygen concentration (f), where the critical oxygen concentration (f_C, black line) and hypoxic oxygen concentration (f_H, brown line) are indicated. The points at which the concentration profiles intersect the critical and hypoxic oxygen concentrations represent the radii (y) for the necrotic and hypoxic regions, respectively, of a given granuloma size.

FIGURE 4.

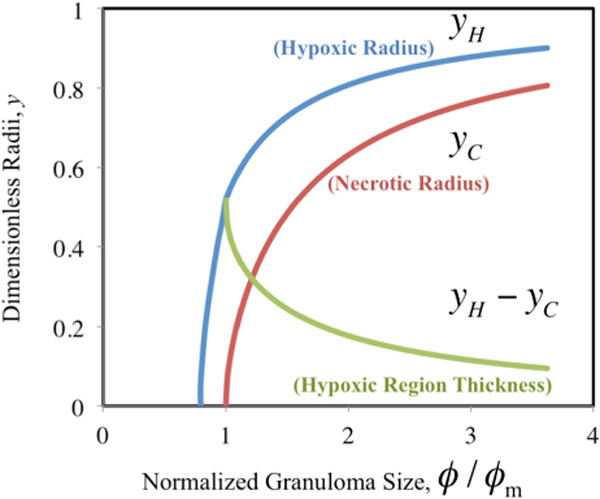
Hypoxic radius (y_H, blue), necrotic radius (y_C, red), and hypoxic region thickness (y_H − y_C, green) as a function of increasing normalized granuloma size (ϕ/ϕ_m).

FIGURE 5.

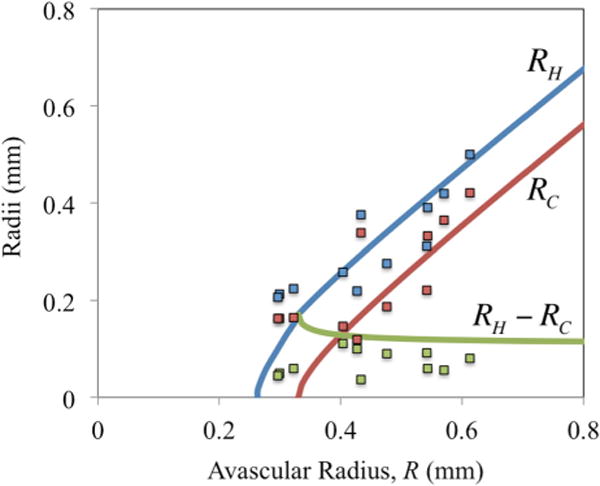
Theoretical (lines) vs. experimental (squares) values of the hypoxic radius (R_H, blue), necrotic radius (R_C, red), and hypoxic region thickness (R_H − R_C, green) of rabbit granulomas as a function of the avascular radius, R (all in mm).

FIGURE 6.

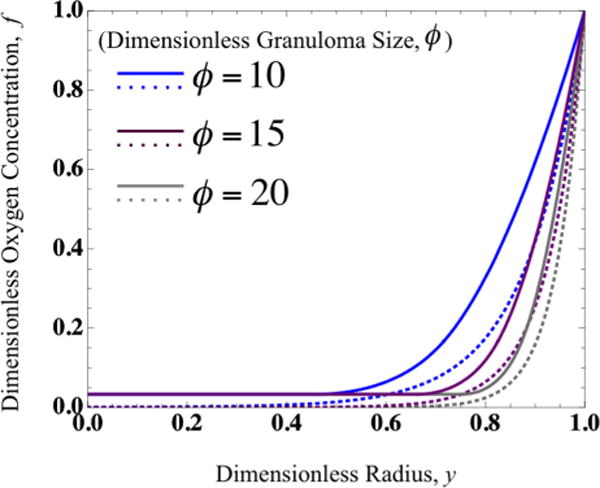
Oxygen concentration profiles (f) vs. granuloma radius (y) for varying granuloma sizes (ϕ) calculated assuming Michaelis–Menten kinetics (dashed lines) vs. limiting-solution kinetics (solid lines).

Numerical Results for Full Michaelis–Menten Kinetics

In the model presented, both the full expression of MM kinetics and the limiting forms of this expression (based on local oxygen concentration) are used to describe oxygen consumption in a TB granuloma. The full MM expression can be solved only numerically for oxygen concentration profiles, as shown in Fig. 3, for various values of the Thiele Modulus (ϕ) which is a dimensionless representation of the granuloma size as scaled with the rates of oxygen consumption and diffusivity (see the Supporting Material). As expected, we find that the oxygen concentration (f) drops quickly with distance into the granuloma core as the granuloma size (ϕ) increases. Further, the necrotic core radius (y = y_C) can be determined graphically from where the numerical MM results intersect a horizontal line set at the critical value at which cells die, i.e., the critical concentration of oxygen (f = f_C); similarly, the hypoxic radius (y = y_H) can be determined graphically from the hypoxic concentration of oxygen (f = f_H).

Figure 3 shows that only larger granulomas (ϕ > 5 corresponding to R > 0.2 mm) are necrotic. Furthermore, it is apparent that the kinetics predict an asymptotic approach to anoxia, i.e., an oxygen concentration of 0 (f = 0), which does not take into account that cells die at a non-zero critical oxygen concentration (f_C) at the edge of the necrotic core where consumption of oxygen ends. This condition, while satisfied in the limiting forms of the MM kinetics, i.e., zero- and first-order kinetics as shown graphically in Fig. 2b (presented next and discussed further in the Supporting Material), stems inherently from the inability of the MM kinetics to account for the fact that the cells die below a critical oxygen level. Therefore, the estimates of concentration profiles and necrotic core size are only approximate using this method.

Comparison of Analytical Solution with Experimental Data for Hypoxic and Necrotic Radii

The size of the hypoxic and necrotic regions of the granuloma can alternately be directly determined via the analytical solutions for the limiting forms of the MM kinetics derived in the Supporting Material. For specified values of hypoxic (f_H) and critical oxygen concentrations (f_C), the hypoxic (y_H) and necrotic (y_C) granuloma radii can be determined for given normalized granuloma size (i.e., the ratio ϕ/ϕ_m, where ϕ_m is the minimum granuloma size with necrosis, as determined experimentally in the Supporting Material), as shown in Fig. 4. Figure 4 also includes the predicted values for the thickness of the hypoxic region (y_H − y_C).

As shown in Fig. 4, no necrotic core exists in small granulomas (ϕ/ϕ_m < 1), although hypoxia can arise. Furthermore, this analysis indicates that the hypoxic and necrotic radii increase dramatically with increasing normalized granuloma size for smaller granulomas ((ϕ/ϕ_m) < 2, corresponding to R < 0.6 mm), but then more gradually for larger granulomas ((ϕ/ϕ_m) > 2), i.e., for granulomas that are at least twice the size of the minimum granuloma particle size where necrosis occurs.

Finally, we recall that the main objective of this model is to predict the emergence of hypoxia and necrosis, and to compare theoretical results to experimental data from the rabbit model of TB. The theoretical dimensionless hypoxic and necrotic radii from Fig. 4 can be, thus, converted to dimensional values (in mm) and compared to experimentally measured values of R_C and R_H via image analysis (see Supplementary Table 1 in the Supporting Material) and plotted vs. R, the avascular granuloma radius from Fig. 2a, as shown in Fig. 5. Note that the model accurately predicts the size of hypoxic and necrotic regions as a function of granuloma size in agreement with the experimental results, and that the hypoxic region thickness (R_H − R_C) approaches a constant value for large granulomas.

Furthermore, from the predictions of the necrotic and hypoxic radii, based on defined critical and hypoxic oxygen concentrations, the oxygen concentration profiles can be plotted piecewise for the avascular region of the granuloma as shown in Fig. 6 for various values of dimensionless granuloma size (ϕ). Note the close agreement between oxygen concentration profiles resulting from the limiting forms of the MM kinetics compared to concentration profiles calculated numerically from the full MM kinetic expression in Fig. 6; in the piecewise solution, the oxygen concentration in the necrotic core is non-zero and cellular consumption ceases at this level (due to cell death).

DISCUSSION

Through mathematical modeling of the underlying transport processes in TB granulomas, we provide a quantitative framework for further understanding of the disease. Our model offers a predictive tool for characterizing oxygen concentration profiles and the amount of hypoxia and necrosis. Although the general concepts used here have been applied to many systems, ranging from catalyst particles¹⁷ to tumor spheroids,³⁵ to our knowledge, this is the first model of oxygen transport in TB granulomas.

Model Features and Limitations

While hypoxia and necrosis, and the potential bacterial adaptations to these harsh microenvironmental conditions, are known to exist in TB granulomas, the root cause of the emergence of these heterogeneous tissue regions has not been elucidated. We propose, based on our recent experimental observations,¹¹ that in TB, as in solid cancerous tumors, these conditions are largely the result of an abnormal granuloma-associated vasculature that results in hypoxia, especially in avascular regions. While other factors have been identified as potential causes of necrosis, such as breakdown of extracellular matrix¹ and immune/inflammatory processes³³ including cell death,³⁰ this work definitively identifies oxygen as a major player in its emergence. While further studies are required to illuminate all of the physiological abnormalities and molecular mechanisms that may contribute to hypoxia and necrosis, the results of this simple model, in agreement with experimental data, quantitatively support the hypothesis that low oxygen supply is a key contributor of necrosis in TB granulomas.

To describe oxygen consumption kinetics in avascular granuloma regions, the model relies on the established Michaelis–Menten (MM) relation. We postulate here, based on the presence of hypoxia as confirmed from tissue histology (described fully in the Supporting Material), that the switch from first-order to zero-order kinetics—the limiting forms of the MM kinetic expression—occurs at a definitive concentration of oxygen at which the cells are metabolically compromised and considered hypoxic. Therefore, this provides a physiological rationale for the switching of the kinetics from zero-order (in abundant oxygen supply) to first-order (in limited oxygen supply).

Our model utilizes physiologically relevant parameters that were either measured a priori or calculated from newly collected data from historical controls from an unpublished animal experiment (as described in the Supporting Material); the results of the model (i.e., the predicted hypoxic and necrotic radii) are compared to experimental measurements from an independent data set. Furthermore, a macroscopic or continuum view of a homogeneous granuloma is employed here. However, this simplifies the varying cellular heterogeneity, functions and metabolic needs of the cell types that comprise a granuloma. For example, this model utilizes kinetic parameters that are assumed to apply to all host cells involved; in reality, lymphocytes, macrophages, and the other cells that comprise granulomas likely have varying metabolic rates and oxygen demands. Further, this model assumes that any bacterial cells in the granuloma metabolize anaerobically; however, it is possible that some surviving bacteria very close to the edge of the necrotic radius or in the hypoxic region may be utilizing oxygen for metabolism. In principle, it should be possible to model stratified layers of a granuloma not only based on local oxygen concentration, but also based on the local major cell type(s) and its corresponding oxygen uptake rate. This could be compared to experimental oxygen concentration profiles within granulomas. Finally, the MM kinetics, although well-accepted, are still only an approximation of cellular consumption kinetics. The actual oxygen consumption kinetics are likely more complex and controlled by the metabolic state of the cell in response to the local supply of oxygen and nutrients in the abnormal granuloma microenvironment.

Conclusions from the Model

The theoretical predictions of the size of the hypoxic and necrotic fractions of granulomas of various sizes seem to compare favorably with experimental results obtained from a rabbit TB model, keeping in mind that all parameters, except for two, were either assigned directly or determined from a priori measurements. In fact, since the ratio of the first-order rate constant for oxygen consumption and oxygen diffusivity can be determined from the minimum size of the granuloma particle with the beginnings of a necrotic core within it based on the definition of the Thiele Modulus for dimensionless granuloma size, as discussed in the Supporting Material, only one of these parameters is independent.

It is also noteworthy that similar to tumor spheroids, the model predicts, in agreement with the TB experimental data, that for granulomas of increasing size, the hypoxic region thickness remains essentially constant, implying that in the avascular region, only the necrotic region is growing with size over time. It is apparent from Fig. 5 that for smaller granulomas (R < 0.3 mm), the theoretical predictions of the hypoxic region thickness do not match as closely with the measured values as with larger granuloma sizes; this is likely because the assumption of one-dimensional transport in a sphere employed for the theoretical model becomes less accurate for smaller granulomas, due to increased surface area to volume ratios, when compared to experimental measurements from non-spherical granulomas.

Future Directions

By continuing to apply mathematical modeling approaches to elucidate the transport and kinetics of small molecules (e.g., glucose, therapeutic drugs) within TB granulomas, additional crucial aspects of the problem can be illuminated. As an example, it would be possible to develop a model of transport and kinetics of small molecules based on an arbitrary-shape representation of the granuloma geometry,⁴ rather than assuming a spherical shape. As another example, exploring the mechanism and kinetics of glycolysis and any aerobic metabolism helping mycobacteria survival within the necrotic core would be of interest. Modeling of TB granulomas would also benefit from improved parameter estimation/measurements (e.g., the effective diffusivity of oxygen).

Of note, the model presented here considers only the avascular (diffusive) region of a granuloma. It would be of great interest to develop a full model of small molecule convection and diffusion throughout the entire granuloma mass, which could further illuminate not only oxygen transport limitations but those of drugs as well, and help in developing chemotherapeutic strategies for overcoming these barriers. For example, we recently discovered that TB granulomas feature an abnormal vasculature that hinders the delivery of oxygen and drugs; we found that “normalizing” this vasculature with an anti-angiogenic agent resulted in improved small molecule delivery and a reduction of hypoxia, without increasing the granuloma bacterial burden.¹¹ We postulate that, when administered in conjunction with anti-TB agents, such adjunct therapies that improve drug and oxygen delivery may enhance drug efficacy and the intra-granuloma immune response, thus benefitting treatment outcome. The effect of adjunct therapies that induce “vascular normalization” could be incorporated into a mathematical model that includes vascular and interstitial convection in order to assess any benefits to vascular function, and thus, drug delivery. Mathematical modeling could also be employed to predict the dosage and timing of such combination treatment strategies, as we have done in cancer,⁴⁵ in order to ensure that the bacteria are eradicated by anti-TB drugs before they can exploit the resulting enhanced oxygenation.

Furthermore, the ability to predict the onset of hypoxia and necrosis in patients, based on granuloma sizes assessed from non-invasive imaging, could lead to altered therapeutic regimens. It is obvious from the TB literature that oxygen—specifically, hypoxia—can have profound and differing effects on MTB vs. host cell survival and metabolism,^{38,39,49–51} and, presumably, disease progression and outcome. If a patient has granulomas that are predicted to be hypoxic via this type of theoretical modeling on the basis of observable lesion size (e.g., from computed tomography scans), they may, for example, be administered pyrazinamide, a drug that has been shown to have anti-MTB effects in hypoxic conditions.⁵⁴ Further, this model can also be readily adapted to predict the penetration of certain drugs into the granuloma based on binding kinetics.

Thus, by continuing to investigate physiological abnormalities and resulting transport limitations in TB granulomas, it is possible to reveal potential avenues through which the availability of oxygen and nutrients to the immune cells can be improved, as well as the delivery of anti-TB drugs to the bacteria that survive within the necrotic core, in an effort to combat this contagion that afflicts a large segment of the world’s population.