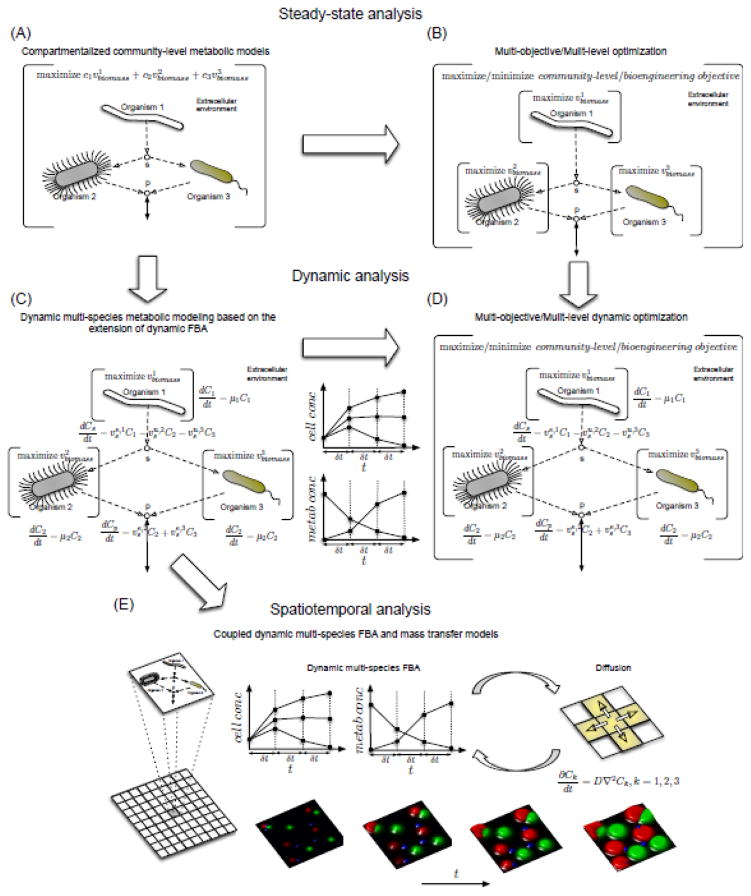
Fig. 4.

Evolution of the metabolic modeling of microbial communities from steady-state to dynamic to spatio-temporal analysis. Brackets represent an optimization problem, empty circles represent shared metabolites (labeled as s and p), dashed arrows represent inter-species metabolic extracellular interactions (metabolite exchanges) and solid arrows denote the uptake and export of metabolites. (A) Steady-state analysis using compartmentalized community-level metabolic models with the objective function being a weighted sum of biomass fluxes of community members ¹⁸¹. (B) Steady-state analysis using a multi-objective and multi-level optimization procedure (a nested optimization problem, where some of the constraints are another optimization problem referred to as inner-level problems ¹⁸⁰). Here, a separate FBA problem is defined for each community member serving as inner-level optimization problems and capturing species-level fitness criteria. These FBA problems are integrated by using constraints in the outer-level problem representing metabolite exchanges among community members. The objective function of the outer-level problem captures a community-level fitness criterion (e.g., maximization of the total community biomass) or a desired community-level bioengineering objective (e.g., the overproduction of a desired compound) ²⁰¹. (C) Dynamic analysis by using the dynamic multi-species metabolic modeling ²⁰³ based on an extension of dynamic FBA for single species ²¹¹. Here, biomass and shared metabolite concentrations are dynamically updated using a finite difference approximation of the conservation of mass equations. A separate FBA problem is solved for each species at each time point to determine their growth rate. (D) Dynamic analysis using a dynamic multi-level and multi-objective optimization procedure that combines procedures in (B) and (C) ²¹⁴. Here, species-level FBA problems are coupled with a community-level or a desired bioengineering objective function using the conservation of mass equations. (E) Spatio-temporal analysis by the direct coupling of dynamic metabolic analysis in (C) and diffusion models ²¹⁵.