Temperature-driven global sea-level variability in the Common Era

Significance

We present the first, to our knowledge, estimate of global sea-level (GSL) change over the last ∼3,000 years that is based upon statistical synthesis of a global database of regional sea-level reconstructions. GSL varied by ∼±8 cm over the pre-Industrial Common Era, with a notable decline over 1000–1400 CE coinciding with ∼0.2 °C of global cooling. The 20th century rise was extremely likely faster than during any of the 27 previous centuries. Semiempirical modeling indicates that, without global warming, GSL in the 20th century very likely would have risen by between −3 cm and +7 cm, rather than the ∼14 cm observed. Semiempirical 21st century projections largely reconcile differences between Intergovernmental Panel on Climate Change projections and semiempirical models.

Abstract

We assess the relationship between temperature and global sea-level (GSL) variability over the Common Era through a statistical metaanalysis of proxy relative sea-level reconstructions and tide-gauge data. GSL rose at 0.1 ± 0.1 mm/y (2σ) over 0–700 CE. A GSL fall of 0.2 ± 0.2 mm/y over 1000–1400 CE is associated with ∼0.2 °C global mean cooling. A significant GSL acceleration began in the 19th century and yielded a 20th century rise that is extremely likely (probability $P\ge 0.95$) faster than during any of the previous 27 centuries. A semiempirical model calibrated against the GSL reconstruction indicates that, in the absence of anthropogenic climate change, it is extremely likely ($P=0.95$) that 20th century GSL would have risen by less than 51% of the observed $13.8\pm 1.5$ cm. The new semiempirical model largely reconciles previous differences between semiempirical 21st century GSL projections and the process model-based projections summarized in the Intergovernmental Panel on Climate Change’s Fifth Assessment Report.

Estimates of global mean temperature variability over the Common Era are based on global, statistical metaanalyses of temperature proxies (e.g., refs. 1–3). In contrast, reconstructions of global sea-level (GSL) variability have relied upon model hindcasts (e.g., ref. 4), regional relative sea-level (RSL) reconstructions adjusted for glacial isostatic adjustment (GIA) (e.g., refs. 5–8), or iterative tuning of global GIA models (e.g., ref. 9). Based primarily on one regional reconstruction (8), the Intergovernmental Panel on Climate Change (IPCC)’s Fifth Assessment Report (AR5) (10) concluded with medium confidence that GSL fluctuations over the last 5 millennia were $<\pm 25$ cm. However, AR5 was unable to determine whether specific fluctuations seen in some regional records (e.g., ref. 5) were global in extent. Similarly, based upon a tuned global GIA model, ref. 9 found no evidence of GSL oscillations exceeding $\sim 15$–20 cm between −2250 and 1800 CE and no evidence of GSL trends associated with climatic fluctuations.

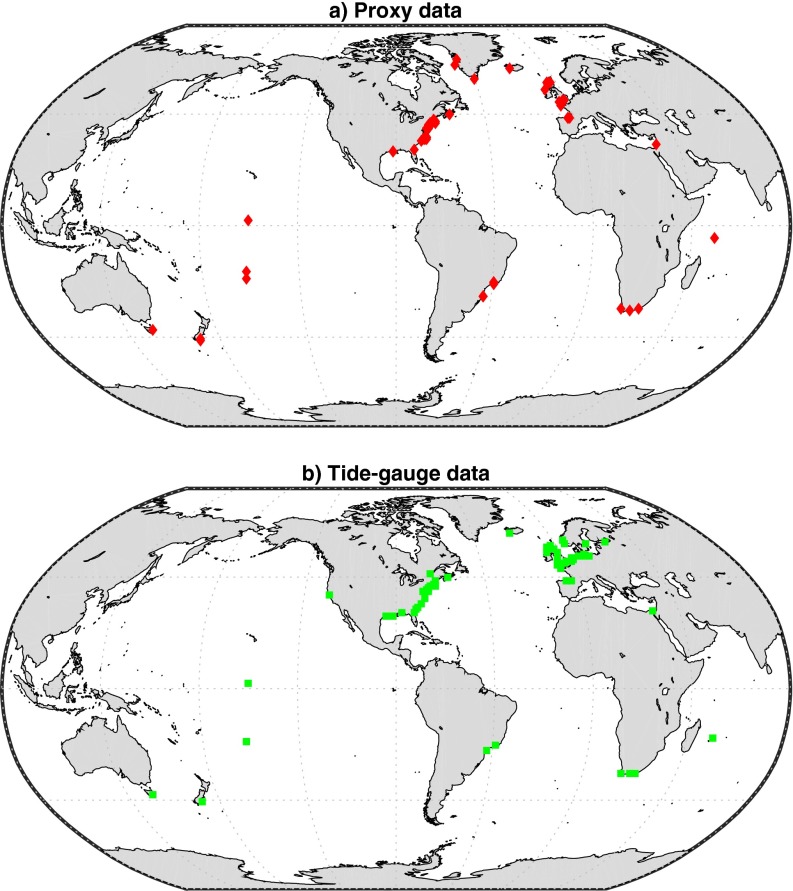
The increasing availability and geographical coverage of continuous, high-resolution Common Era RSL reconstructions provides a new opportunity to formally estimate GSL change over the last ∼3,000 years. To do so, we compiled a global database of RSL reconstructions from 24 localities (Dataset S1, a and Fig. S1A), many with decimeter-scale vertical resolution and subcentennial temporal resolution. We augment these geological records with 66 tide-gauge records, the oldest of which (11) begins in 1700 CE (Dataset S1, b and Fig. S1B), as well as a recent tide-gauge–based estimate of global mean sea-level change since 1880 CE (12).

Fig. S1.

Locations of sites with (A) proxy data and (B) tide-gauge data included in the analysis.

To analyze this database, we construct a spatiotemporal empirical hierarchical model (13, 14) that distinguishes between sea-level changes that are common across the database and those that are confined to smaller regions. The RSL field $f\left(\mathbf{x},t\right)$ is represented as the sum of three components, each with a Gaussian process (GP) prior (15),

$$f\left(\mathbf{x},t\right)=g\left(t\right)+l\left(\mathbf{x}\right)\left(t-t_0\right)+m\left(\mathbf{x},t\right).$$ [1]

Here, $\mathbf{x}$ represents spatial location, t represents time, and $t_0$ is a reference time point (2000 CE). The three components are (i) GSL $g\left(t\right)$, which is common across all sites and primarily represents contributions from thermal expansion and changing land ice volume; (ii) a regionally varying, temporally linear field $l\left(\mathbf{x}\right)\left(t-t_0\right)$, which represents slowly changing processes such as GIA, tectonics, and natural sediment compaction; and (iii) a regionally varying, temporally nonlinear field $m\left(\mathbf{x},t\right)$, which primarily represents factors such as ocean/atmosphere dynamics (16) and static equilibrium “fingerprint” effects of land−ice mass balance changes (17, 18). The regional nonlinear field also incorporates small changes in rates of GIA, tectonics, and compaction that occur over the Common Era. The incorporation of the regionally correlated terms $l\left(\mathbf{x}\right)\left(t-t_0\right)$ and $m\left(\mathbf{x},t\right)$ ensures that records from regions with a high density of observations are not unduly weighted in estimating the common GSL signal $g\left(t\right)$.

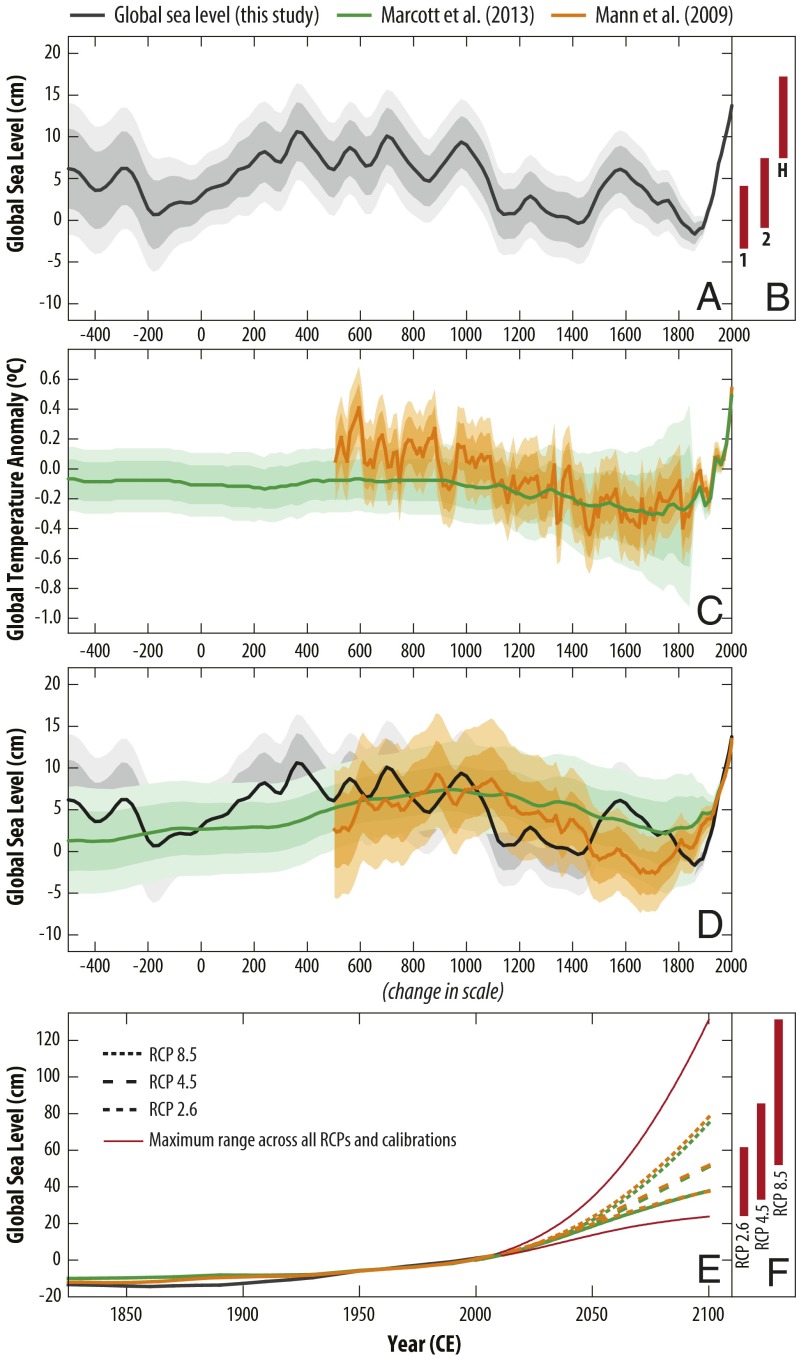
Because a constant-rate trend in $g\left(t\right)$ could also be interpreted as a regional linear trend that is present at all reconstruction sites but is not truly global, we condition the model on the assumption that mean GSL over −100–100 CE is equal to mean GSL over 1600–1800 CE and focus on submillennial variations (Fig. 1A). We chose the first window to encompass the beginning of the Common Era and the last window to cover the last 2 centuries before the development of a tide-gauge network outside of northern Europe.

Fig. 1.

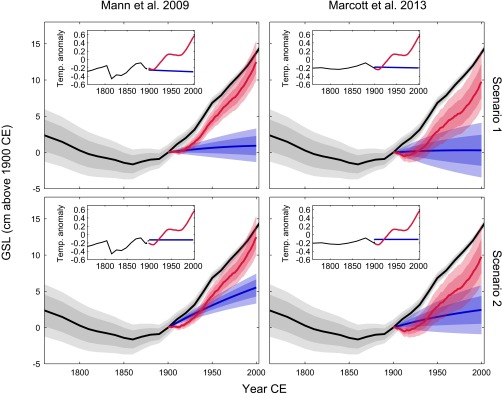
(A) Global sea level (GSL) under prior ML_2,1. Note that the model is insensitive to small linear trends in GSL over the Common Era, so the relative heights of the 300–1000 CE and 20th century peaks are not comparable. (B) The 90% credible intervals for semiempirical hindcasts of 20th century sea-level change under historical temperatures (H) and counterfactual scenarios 1 and 2, using both temperature calibrations. (C) Reconstructions of global mean temperature anomalies relative to the 1850–2000 CE mean (1, 2). (D) Semiempirical fits to the GSL curve using the two alternative temperature reconstructions. (E) As in B, including 21st century projections for RCPs 2.6, 4.5, and 8.5. Red lines show the fifth percentile of RCP 2.6 and 95th percentile of RCP 8.5. (F) The 90% credible intervals for 2100 by RCP. In A, B, and D, values are with respect to 1900 CE baseline; in E and F, values are with respect to 2000 CE baseline. Heavy shading, 67% credible interval; light shading, 90% credible interval.

The priors for each component are characterized by hyperparameters that comprise amplitudes (for all three components), timescales of variability [for $g\left(t\right)$ and $m\left(\mathbf{x},t\right)$], and spatial scales of variability [for $l\left(\mathbf{x}\right)$ and $m\left(\mathbf{x},t\right)$] (Dataset S1, c). We consider five priors with different hyperparameters (see Supporting Information). The presented rates are taken from prior ML_2,1, which is optimized under the assumption that the a priori timescales of variability in global and regional sea-level change are the same. Results from the four alternative priors are presented in Supporting Information. Quoted probabilities are conservatively taken as minima across all five priors. Illustrative fits at specific sites are shown in Fig. S2.

Fig. S2.

Model fits under prior ML_2,1 at eight illustrative sites: (A) East River Marsh, CT; (B) Sand Point, NC, (C) Vioarholmi, Iceland, (D) Loch Laxford, Scotland, (E) Sissimut, Greenland, (F) Caesarea, Israel, (G) Christmas Island, Kiribati, and (H) Kariega Estuary, South Africa. (Note that the model fit at each site is informed by all observations, not just those at the illustrated site.) Red boxes show all data points within 0.1 degrees of the centroid of the named site. Errors are $\pm 2\sigma$.

Results and Discussion

Common Era Reconstruction.

Pre-20th-century Common Era GSL variability was very likely (probability $P=0.90$) between $\sim \pm 7$ cm and $\pm 11$ cm in amplitude (Fig. 1A and Dataset S1, e). GSL rose from 0 CE to 700 CE ($P\ge 0.98$) at a rate of $0.1\pm 0.1$ mm/y (2σ), was nearly stable from 700 CE to 1000 CE, then fell from 1000 CE and 1400 CE ($P\ge 0.98$) at a rate of $0.2\pm 0.2$ mm/y (Fig. 1A). GSL likely rose from 1400 CE to 1600 CE ($P\ge 0.75$) at $0.3\pm 0.4$ mm/y and fell from 1600 CE to 1800 CE ($P\ge 0.86$) at $0.3\pm 0.3$ mm/y.

Historic GSL rise began in the 19th century, and it is very likely ($P\ge 0.93$) that GSL has risen over every 40-y interval since 1860 CE. The average rate of GSL rise was $0.4\pm 0.5$ mm/y from 1860 CE to 1900 CE and $1.4\pm 0.2$ mm/y over the 20th century. It is extremely likely ($P\ge 0.95$) that 20th century GSL rise was faster than during any preceding century since at least −800 CE.

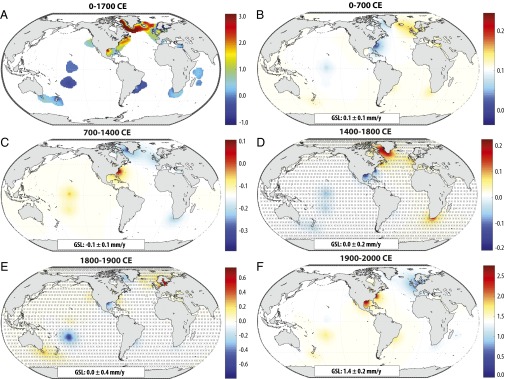
The spatial coverage of the combined proxy and long-term tide-gauge dataset is incomplete. The available data are sufficient to reduce the posterior variance in the mean 0–1700 CE rate by $>10\text{\%}$ relative to the prior variance along coastlines in much of the North Atlantic and the Gulf of Mexico, and parts of the Mediterranean, the South Atlantic, the South Pacific, and Australasia (Fig. 2A). High-resolution proxy records are notably lacking from Asia, most of South America, and most of Africa. Nevertheless, despite the incomplete coverage and regional variability, sensitivity analyses of different data subsets indicate that key features of the GSL curve—a rise over 0–700 CE, a fall over 1000–1400 CE, and a rise beginning in the late 19th century—are not dependent on records from any one region (Dataset S1, f). By contrast, the rise over 1400–1600 CE and fall over 1600–1800 CE are not robust to the removal of data from the western North Atlantic.

Fig. 2.

(A) Mean estimated rate of change (millimeters per year) over 0–1700 CE under prior ML_2,1. In shaded areas, conditioning on the observations reduces the variance by at least 10% relative to the prior. (B−F) Mean estimated rates of change (mm/y) from (B) 0–700 CE, (C) 700–1400 CE, (D) 1400–1800 CE, (E) 1800–1900 CE, and (F) 1900–2000 CE, after removing the 0–1700 CE trend. Areas where a rise and a fall are about equally likely ($P=$ 0.33–0.67) are crosshatched. The color scales are centered around the noted rate of GSL change.

On millennial and longer timescales, regional RSL change can differ significantly from GSL change as a result of GIA, tectonics, and sediment compaction (Fig. 2). For example, over 0–1700 CE, RSL rose at $1.5\pm 0.1$ mm/y in New Jersey, on the collapsing forebulge of the former Laurentide Ice Sheet, and fell at $0.1\pm 0.1$ mm/y on Christmas Island, in the far field of all late Pleistocene ice cover (Dataset S1, g). Detrended RSL (after removal of the average 0–1700 CE rate) reveals notable patterns of temporal variability, especially in the western North Atlantic, where the highest-resolution reconstructions exist. Rates of RSL change in New Jersey and North Carolina vary from the long-term mean in opposite directions over 0–700 CE and 1000–1400 CE (Fig. 2 and Dataset S1, g). Over 0–700 CE, a period over which GSL rose at $0.1\pm 0.1$ mm/y, detrended RSL rose in New Jersey ($P\ge 0.91$) while it fell in North Carolina ($P\ge 0.88$). Conversely, over 1000–1400 CE, while GSL was falling, detrended RSL fell in New Jersey ($P>0.90$) while it rose in North Carolina ($P\ge 0.99$). This pattern is consistent with changes in the Gulf Stream (16) or in mean nearshore wind stress (19). If driven by the Gulf Stream, it suggests a weakening or polar migration of the Gulf Stream over 0–700 CE, with a strengthening or equatorial migration occurring over 1000–1400 CE.

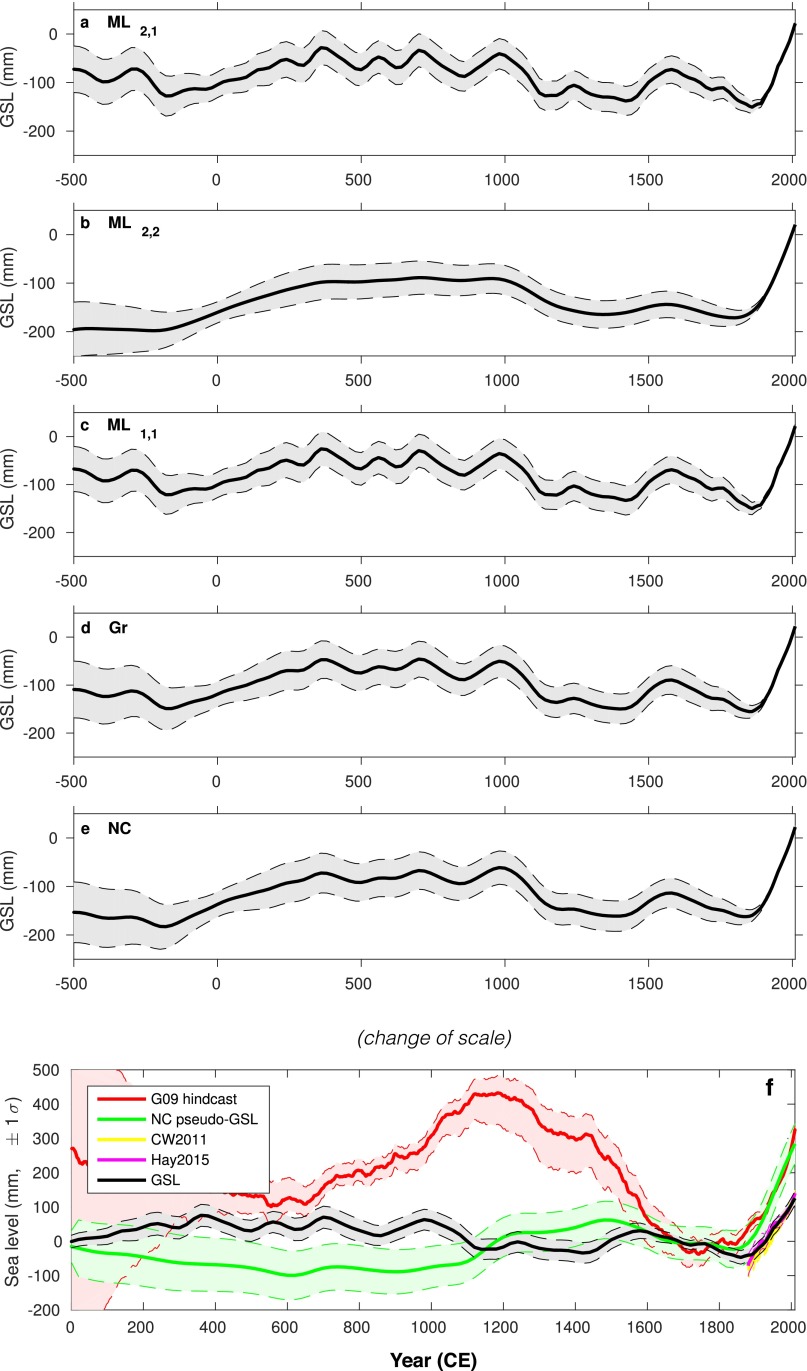
Our estimate differs markedly from previous reconstructions of Common Era GSL variability (5, 6, 9, 20) (Fig. S3F). For example, the ref. 20 hindcast predicts GSL swings with ∼4× larger amplitude, and it includes a rise from 650 CE to 1200 CE (a period of GSL stability and fall in the data-based estimate) and a fall from 1400 CE to 1700 CE (a period of approximate GSL stability in the data-based estimate). The curve derived from the detrended North Carolina RSL reconstruction (5) indicates an amplitude of change closer to our GSL reconstruction but differs in phasing from it, with a relatively high sea level during $\sim 1200$–1500 CE likely reflecting the regional processes mentioned above. The globally tuned GIA model of ref. 9, which includes 31 data points from the last millennium (compared with 790 proxy data points in our analysis), found no systematic GSL changes over the Common Era.

Fig. S3.

(A–E) GSL estimates under priors (A) ML_2,1, (B) ML_2,2, (C) ML_1,1, (D) Gr, and (E) NC. (F) GSL reconstruction under prior ML_2,1 (black) compared with the hindcast of ref. 20 (G09 hindcast; red), a curve derived from the North Carolina RSL curve by detrending and the addition of $\pm 10$ mm ($2\sigma$) errors after ref. 5 (NC pseudo-GSL; green), and the 19th–20th century GMSL reconstructions of ref. 12 (Hay2015; magenta) and ref. 106 (CW2011; yellow). Multicentury records are aligned relative to the 1600–1800 CE average; 19th–20th century reconstructions are aligned to match our GSL reconstruction in 2000 CE. Errors are $\pm 1\sigma$.

Twentieth Century GSL Rise.

Semiempirical models of GSL change, based upon statistical relationships between GSL and global mean temperature or radiative forcing, provide an alternative to process models for estimating future GSL rise (e.g., refs. 20–23) and generating hypotheses about past changes (e.g., refs. 4, 20, and 24). The underlying physical assumption is that GSL is expected to rise in response to climatic warming and reach higher levels during extended warm periods, and conversely during cooling and extended cool periods. Ref. 5 generated the first semiempirical GSL model calibrated to Common Era proxy data, but relied upon sea-level data from a single region rather than a global synthesis.

Our new GSL curve shows that multicentury GSL variability over the Common Era shares broad commonalities with global mean temperature variability, consistent with the assumed link that underlies semiempirical models. For example, the $9\pm 8$ cm GSL fall over 1000–1400 CE coincides with a ∼0.2 °C decrease in global mean temperature, and the $9\pm 3$ cm GSL rise over 1860–1960 CE coincides with ∼0.2 °C warming (2). Motivated by these commonalities, using our GSL reconstruction and two global mean temperature reconstructions (1, 2), we construct a semiempirical GSL model that is able to reproduce the main features of GSL evolution (Fig. 1 B and C).

To assess the anthropogenic contribution to GSL rise, we consider two hypothetical global mean temperature scenarios without anthropogenic warming. In scenario 1, the gradual temperature decline from 500 CE to 1800 CE is taken as representative of Earth’s long-term, late Holocene cooling (2), and, in 1900 CE, temperature returns to a linear trend fit to 500–1800 CE. In scenario 2, we assume that 20th century temperature stabilizes at its 500–1800 CE mean. The difference between GSL change predicted under these counterfactuals and that predicted under observed temperatures represents two alternative interpretations of the anthropogenic contribution to GSL rise (Table 1, Fig. 1A, and Fig. S4). Both scenarios show a dominant human influence on 20th century GSL rise.

Table 1.

Hindcasts of 20th century GSL rise (centimeters)

Scenario	Summary		Calibrated to individual temperature reconstructions
			Mann et al. (1)		Marcott et al. (2)
	50th percentile	5th–95th percentile	50th percentile	5th–95th percentile	50th percentile	5th–95th percentile
Observed	13.8	12.6–15.0
Historical	13.0	7.7–17.5	14.3	11.5–17.5	11.6	7.7–16.3
Scenario 1	0.6	−3.5–4.1	0.9	−1.3–3.3	0.3	−3.5–4.1
Scenario 2	4.0	−0.9–7.5	5.5	3.3–7.5	2.4	−0.9–5.9
Percent of historical
Scenario 1	5	−27–41	7	−9–23	3	−27–41
Scenario 2	30	−10–51	39	24–51	21	−10–42

All values are with respect to year 1900 CE baseline. Summary results show means of medians, minima of lower bounds, and maxima of upper bounds taken across both temperature calibrations.

Fig. S4.

Counterfactual hindcasts of global mean sea-level rise in the absence of anthropogenic warming. Each row assumes a different counterfactual temperature scenario (see Materials and Methods), while each column represents model calibration to a different temperature reconstruction (Inset). In the temperature Insets, the black lines represent the original temperature reconstruction to 1900, the red line represents the HadCRUT4 temperature reconstruction for the 20th century, and the blue line represents the counterfactual scenario. In the main plots, the red and blue curves correspond, respectively, to the HadCRUT4 and counterfactual temperature scenarios. The difference between them can be interpreted as the anthropogenic GSL rise. Heavy shading, 67% credible; light shading, 90% credible.

The hindcast 20^th century GSL rise, driven by observed temperatures, is ∼13 cm, with a 90% credible interval of 7.7–17.5 cm. This is consistent with the observed GSL rise of $13.8\pm 1.5$ cm, which is due primarily to contributions from thermal expansion and glacier mass loss (25). Of the hindcast 20th century GSL rise, it is very likely ($P=0.90$) that −27% to +41% of the total (scenario 1) or −10% to +51% of the total (scenario 2) would have occurred in the absence of anthropogenic warming. Under all calibrations and scenarios, it is likely ($P\ge 0.88$) that observed 20th century GSL rise exceeded the nonanthropogenic counterfactuals by 1940 CE and extremely likely ($P\ge 0.95$) that it had done so by 1950 CE (Dataset S1, h). The GSL rise in the alternative scenarios is related to the observation that global mean temperature in the early 19th century was below the 500–1800 CE trend (and thus below the 20th century in scenario 1) and, for most of the 19th century, was below the 500–1800 CE mean (and thus below the 20th century in scenario 2) (Fig. S4).

The estimates of the nonanthropogenic contribution to 20th century GSL rise are similar to ref. 4’s semiempirical estimate of 1–7 cm. They are also comparable to the detrended fluctuation analysis estimates of refs. 26 and 27, which found it extremely likely that < ∼40% of observed GSL rise could be explained by natural variability. These previous estimates, however, could have been biased low by the short length of the record used. The 3,000-y record underlying our estimates provides greater confidence.

Projected 21st Century GSL Rise.

The semiempirical model can be combined with temperature projections for different Representative Concentration Pathways (RCPs) to project future GSL change (Table 2, Fig. 1D, and Dataset S1, i). RCPs 8.5, 4.5, and 2.6 correspond to high-end “business-as-usual” greenhouse gas emissions, moderate emissions abatement, and extremely strong emissions abatement, respectively. They give rise to very likely ($P=0.90$) GSL rise projections for 2100 CE (relative to 2000 CE) of 52–131 cm, 33–85 cm, and 24–61 cm, respectively. Comparison of the RCPs indicates that a reduction in 21st century sea-level rise of ∼30 to 70 cm could be achieved by strong mitigation efforts (RCP 2.6), even though sea level is a particularly “slow-responding” component of the climate system.

Table 2.

Projections of 21st century GSL rise (centimeters)

Method	This study semiempirical			AR5 (29) assessment		Schaeffer et al. (23) semiempirical		Kopp et al. (30) bottom-up			Horton et al. (31) survey
	50th percentile	17th–83rd percentile	5th–95th percentile	50th percentile	17th–83rd percentile	50th percentile	5th–95th percentile	50th percentile	17th–83rd percentile	5th–95th percentile	17th–83rd percentile	5th–95th percentile
RCP 2.6	38	28–51	24–61	43	28–60	75	52–96	50	37–65	29–82	40–60	25–70
RCP 4.5	51	39–69	33–85	52	35–70	90	64–121	59	45–77	36–93	n.a.	n.a.
RCP 8.5	76	59–105	52–131	73	53–97	n.c.	n.c.	79	62–100	55–121	70–120	50–150

All values are with respect to year 2000 CE baseline except AR5, which is with respect to the 1985–2005 CE average. Results from this study show mean of medians, minima of lower bounds, and maxima of upper bounds. n.a., not asked; n.c., not calculated.

Since ref. 21 inaugurated the recent generation of semiempirical models with its critique of the process model-based GSL projections of the IPCC’s Fourth Assessment Report (AR4) (28), semiempirical projections have generally exceeded those based upon process models. While AR5’s projections (29) were significantly higher than those of AR4, semiempirical projections (e.g., ref. 23) have continued to be higher than those favored by the IPCC. However, our new semiempirical projections are lower than past results, and they overlap considerably with those of AR5 (29) and of ref. 30, which used a bottom-up probabilistic estimate of the different factors contributing to sea-level change. They also agree reasonably well with the expert survey of ref. 31 (Table 2). Our analysis thus reconciles the remaining differences between semiempirical and process-based models of 21st century sea-level rise and strengthens confidence in both sets of projections. However, both semiempirical and process model-based projections may underestimate GSL rise if new processes not active in the calibration period and not well represented in process models [e.g., marine ice sheet instability in Antarctica (32)] become major factors in the 21st century.

Conclusions

We present, to our knowledge, the first Common Era GSL reconstruction that is based upon the statistical integration of a global database of RSL reconstructions. Estimated GSL variability over the pre-20th century Common Era was very likely between $\sim \pm 7$ cm and $\sim \pm 11$ cm, which is more tightly bound than the $<\pm 25$ cm assessed by AR5 (10) and smaller than the variability estimated by a previous semiempirical hindcast (4). The most robust pre-Industrial signals are a GSL increase of $0.1\pm 0.1$ mm/y from 0 CE to 700 CE and a GSL fall of $0.2\pm 0.2$ mm/y from 1000 CE to 1400 CE. The latter decline coincides with a decline in global mean temperature of ∼0.2 °C, motivating the construction of a semiempirical model that relates the rate of GSL change to global mean temperature. Counterfactual hindcasts with this model indicate that it is extremely likely ($P=0.95$) that less than about half of the observed 20th century GSL rise would have occurred in the absence of global warming, and that it is very likely ($P=0.90$) that, without global warming, 20th century GSL rise would have been between −3 cm and +7 cm, rather than the observed 14 cm. Forward projections indicate a very likely 21st century GSL rise of 52–131 cm under RCP 8.5 and 24–61 cm under RCP 2.6, values that provide greater consistency with process model-based projections preferred by AR5 than previous semiempirical projections.

Materials and Methods

Sea-Level Records.

The database of RSL reconstructions (Dataset S2) was compiled from published literature, either directly from the original publications or by contacting the corresponding author (5, 7, 8, 33–89). The database is not a complete compilation of all sea-level index points from the last ∼3,000 years. Instead, we include only those reconstructions that we qualitatively assessed as having sufficient vertical and temporal resolution and density of data points to allow identification of nonlinear variations, should they exist. This assessment was primarily based on the number of independent age estimates in each record. Where necessary and possible, we also included lower-resolution reconstructions to ensure that long-term linear trends were accurately captured if the detailed reconstruction was of limited duration. For example, the detailed reconstruction from the Isle of Wight (69) spans only the last 300 y, and we therefore included a nearby record that described regional RSL trends in southwest England over the last 2,000 y (51).

Each database entry includes reconstructed RSL, RSL error, age, and age error. For regional reconstructions produced from multiple sites (e.g., ref. 5), we treated each site independently. Where we used publications that previously compiled RSL reconstructions (e.g., refs. 37 and 45), the results were used as presented in the compilation. RSL error was assumed to be a $2\sigma$ range unless the original publication explicitly stated otherwise or if the reconstruction was generated using a transfer function and a Random Mean SE Standard Error of Prediction was reported, in which case this was treated as a $1\sigma$ range. We did not reinterpret or reanalyze the published data, except for the South American data (33, 59, 71, 90) that were mostly derived from marine mollusks (vermetids). The radiocarbon ages for these data were recalibrated using a more recent marine reservoir correction (91) and the IntCal13 and MARINE13 radiocarbon age calibration curves (92).

Tide gauge records were drawn from the Permanent Service for Mean Sea Level (PSMSL) (93, 94). We included all records that were either (i) longer than 150 y, (ii) within 5 degrees distance of a proxy site and longer than 70 y, or (iii) the nearest tide gauge to a proxy site that is longer than 20 y (Dataset S1, b). We complement these with multicentury records from Amsterdam (1700–1925 CE) (11), Kronstadt (1773–1993 CE) (95), and Stockholm (1774–2000 CE) (96), as compiled by PSMSL. Annual tide-gauge data were smoothed by fitting a temporal GP model to each record and then transforming the fitted model to decadal averages, both for computational efficiency and because the decadal averages more accurately reflect the recording capabilities of proxy records.

To incorporate information from a broader set of tide-gauge records, we also included decadal averages from the Kalman smoother-estimated GSL for 1880–2010 CE of ref. 12. Off-diagonal elements of the GSL covariance matrix were derived from an exponential decay function with a 3-y decorrelation timescale. This timescale was set based on the mean temporal correlation coefficient across all tide gauges using the annual PSMSL data, which approaches zero after 2 y.

Spatiotemporal Statistical Analysis.

Hierarchical models (for a review targeted at paleoclimatologists, see ref. 14) divide into different levels. The hierarchical model we use separates into (i) a data level, which models how the spatiotemporal sea-level field is recorded, with vertical and temporal noise, by different proxies; (ii) a process level, which models the latent spatiotemporal field of RSL described by Eq. 1; and (iii) a hyperparameter level. We used an empirical Bayesian analysis method, meaning that, for computational efficiency, the hyperparameters used are point estimates calibrated in a manner informed by the data (and described in greater detail in Supporting Information); thus, our framework is called an empirical hierarchical model. The output of the hierarchical model includes a posterior probability distribution of the latent spatiotemporal field $f\left(\mathbf{x},t\right)$, conditional on the point estimate hyperparameters. (Dataset S3 provides the full time series and covariance of the posterior estimate of GSL.) Our use of GP priors at the process level and normal likelihoods at the data level renders the calculation of this conditional posterior analytically tractable (15).

At the data level, the observations $y_i$ are modeled as

$$y_i=f\left({\mathbf{x}}_i,t_i\right)+w\left({\mathbf{x}}_i,t_i\right)+y_0\left({\mathbf{x}}_i\right)+{\mathit{ϵ}}_i^y$$ [2]

$$t_i={\widehat{t}}_i+{\mathit{ϵ}}_i^t$$ [3]

$$w\left(\mathbf{x},t\right)\approx \mathcal{G}\mathcal{P}\left\{0,{\sigma }_w^2\hspace{0.17em}\delta \left(\mathbf{x},\mathbf{x}\prime \right)\hspace{0.17em}\delta \left(t,t\prime \right)\right\}$$ [4]

$$y_0\left(\mathbf{x}\right)\approx \mathcal{G}\mathcal{P}\left\{0,{\sigma }_0^2\hspace{0.17em}\delta \left(\mathbf{x},\mathbf{x}\prime \right)\right\}$$ [5]

where ${\mathbf{x}}_i$ is the spatial location of observation i, $t_i$ is its age, $w\left(\mathbf{x},t\right)$ is a white noise process that captures sea-level variability at a subdecadal level (which we treat here as noise), ${\widehat{t}}_i$ is the mean observed age, ${\mathit{ϵ}}_i^t$ and ${\mathit{ϵ}}_i^y$ are errors in the age and sea-level observations, $y_0\left(\mathbf{x}\right)$ is a site-specific datum offset, and δ is the Kronecker delta function. The notation $\mathcal{G}\mathcal{P}\left\{\mu ,k\left(x,x\prime \right))\right\}$ denotes a GP with mean μ and covariance function $k\left(x,x\prime \right)$. For tide gauges, ${\mathit{ϵ}}^t$ is zero and the distribution of ${\mathit{ϵ}}^y$ is estimated during the GP smoothing process, in which annual tide-gauge averages are assumed to have uncorrelated, normally distributed noise with SD 3 mm. For proxy data, ${\mathit{ϵ}}^t$ and ${\mathit{ϵ}}^y$ are treated as independent and normally distributed, with an standard deviation (SD) specified for each data point based on the original publication. Geochronological uncertainties are incorporated using the noisy input GP method of ref. 97, which uses a first-order Taylor series approximation of the latent process to translate errors in the independent variable into errors in the dependent variable,

$$f\left({\mathbf{x}}_i,t_i\right)\approx f\left({\mathbf{x}}_i,{\widehat{t}}_i\right)+{\mathit{ϵ}}_i^t\frac{\partial f\left({\mathbf{x}}_i,{\widehat{t}}_i\right)}{\partial t}.$$ [6]

The assumption that mean GSL over −100–100 CE is equal to mean GSL over 1600–1800 CE is implemented by conditioning on a set of pseudodata with very broad uncertainties (SD of 100 m on each individual pseudodata point) and a correlation structure that requires equality in the mean levels over the two time windows.

At the process level, the GP priors for $g\left(t\right)$, $l\left(\mathbf{x}\right)$ and $m\left(\mathbf{x},t\right)$ are given by

$$g\left(t\right)\approx \mathcal{G}\mathcal{P}\left\{0,{\sigma }_{g0}^2+{\sigma }_g^2\rho \left(t,t\prime ;{\tau }_g\right)\right\}$$ [7]

$$l\left(\mathbf{x}\right)\approx \mathcal{G}\mathcal{P}\left\{\text{ICE}5\text{G}\left(\mathbf{x}\right),{\sigma }_l^2\gamma \left(\mathbf{x},\mathbf{x}\prime ;{\lambda }_l\right)\right\}$$ [8]

$$m\left(\mathbf{x},t\right)\approx \mathcal{G}\mathcal{P}\left\{0,{\sigma }_m^2\gamma \left(\mathbf{x},\mathbf{x}\prime ;{\lambda }_m\right)\rho \left(t,t\prime ;{\tau }_m\right)\right\}.$$ [9]

Here, $\text{ICE}5\text{G}\left(\mathbf{x}\right)$ denotes the GIA rate given by the ICE5G-VM2-90 model of ref. 98 for 1700–1950 CE. The temporal correlation function $\rho \left(t,t\prime ;\tau \right)$ is a Matérn correlation function with smoothness parameter 3/2 and scale τ. (The choice of smoothness parameter 3/2 implies a functional form in which the first temporal derivative is everywhere defined.) The spatial correlation $\gamma \left(\mathbf{x},\mathbf{x}\prime ;\lambda \right)$ is an exponential correlation function parameterized in terms of the angular distance between $\mathbf{x}$ and $\mathbf{x}\prime$.

The hyperparameters of the model include the prior amplitudes ${\sigma }_{g0}$, which is a global datum offset (for ML_2,1, 118 mm); ${\sigma }_g$, which is the prior amplitude of GSL variability (for ML_2,1, 67 mm); ${\sigma }_l$, which is the prior SD of slopes of the linear rate term (for ML_2,1, 1.1 mm/y); and ${\sigma }_m$, which is the prior amplitude of regional sea-level variability (for ML_2,1, 81 mm). They also include the timescales of global and regional variability, ${\tau }_g$ and ${\tau }_m$ (for ML_2,1, 136 y), the spatial scale of regional sea-level variability ${\lambda }_m$ (for ML_2,1, 7.7°), and the spatial scale of deviations of the linear term from the ICE5G-VM2-90 GIA model, ${\lambda }_l$ (for ML_2,1, 5.9°). In the ML_2,1 results presented in the main text, it is assumed that ${\tau }_g={\tau }_m$; four alternative sets of assumptions and calibrations of the hyperparameters are described in Supporting Information.

Semiempirical Sea-Level Model.

Our semiempirical sea-level model relates the rate of GSL rise $dh/dt$ to global mean temperature $T\left(t\right)$,

$$dh/dt=a\left(T\left(t\right)-T_0\left(t\right)\right)+c\left(t\right)$$ [10]

with

$$d{T}_0\left(t\right)/dt=\left(T\left(t\right)-T_0\left(t\right)\right)/{\tau }_1$$

$$dc\left(t\right)/dt=c/{\tau }_2,$$

where a is the sensitivity of the GSL rate to a deviation of $T\left(t\right)$ from an equilibrium temperature $T_0\left(t\right)$, ${\tau }_1$ is the timescale on which the actual temperature relaxes toward the equilibrium temperature, and c is a temperature-independent rate term with e-folding time ${\tau }_2$. The first term describes the GSL response to climate change during the study period. The second term covers a small residual trend arising from the long-term response to earlier climate change (i.e., deglaciation), which is very slowly decaying over millennia and of the order 0.1 mm/y in 2000 CE. It thus has a negligible effect on the modeled GSL rise during the 20th and 21st centuries.

By comparison with Eq. 2, ref. 5 used the formulation

$$dh/dt=a_1\left(T\left(t\right)-T_{\mathrm{0,0}}\right)+a_2\left(T\left(t\right)-T_0\left(t\right)\right)+b\left(dT/dt\right).$$ [11]

The present model has two differences from that of ref. 5. First, we substitute the temperature-independent term $c\left(t\right)$ for term $a_1\left(T\left(t\right)-T_{\mathrm{0,0}}\right)$ and thus eliminate the temperature dependence in this term. This modified term describes a very slow component of sea-level adjustment that can capture the tail end of the response to the last deglaciation. Second, we omit the fast response term $b\left(dT/dt\right)$ because it is of no consequence on the long timescales considered here.

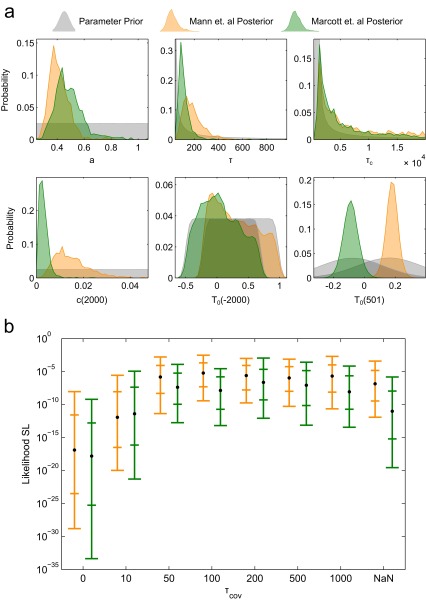
We sample the posterior probability distribution of the parameter set $\mathbf{\Psi }=\left\{c\left(t\right),T_0\left(t\right),a,{\tau }_1,{\tau }_2\right\}$, specified as $P\left(\mathbf{\Psi }|g\left(t\right),T\left(t\right)\right)$, using a Metropolis−Hastings (MH) algorithm (99) (Fig. S5A and Dataset S1, j). The starting parameter set is a maximum-likelihood set, determined by simulated annealing. Sampled Markov Chains are thinned to every 500th sample, with the first 1,000 samples discarded in a burn-in period.

Fig. S5.

(A) Probability distributions of semiempirical model parameters. Prior distributions (gray) are not shown in full where scaling axes to display them would render posteriors obscure. (B) Likelihood of different values of ${\tau }_{cov}$. Black dots show likelihoods across all semiempirical projections, and the bars show the 5th/17th/83rd/95th percentile conditional likelihoods for individual semiempirical projections. A value of ${\tau }_{cov}=100$ y is used in the analysis. Orange [green] represents calibration with the Mann et al. (1) [Marcott et al. (2)] temperature curve.

We use two alternative temperature reconstructions (Fig. 1B): (i) the global regularized expectation-maximization (RegEM) climate field reconstruction (CFR) temperature proxy of Mann et al. (1), incorporating the HadCRUT3 instrumental data of ref. 100 after 1850 CE, and (ii) the Marcott et al. (2) RegEM global reconstruction. We use 11-y averages from the Mann et al. reconstruction’s annual values, whereas the Marcott et al. reconstruction reports 20-y average values. Because the number of proxy data in the Marcott et al. reconstruction decreases toward present, we combine it with 20-y averages from the HadCRUT3 data (100) and align them over their period of overlap (1850–1940 CE). The two temperature reconstructions are generally in good agreement, although the Marcott et al. record shows ∼0.2 °C lower temperatures before $\sim 1100$ CE. This overall agreement provides confidence that the true global temperature is represented within the uncertainties of the records, whereas the modest differences motivate the use of both records to provide a more realistic representation of uncertainty in the calculated GSL.

We denote the temperature reconstruction as $S\left(t\right)$ and treat it as noisy observations of $T\left(t\right)$; i.e., $\mathbf{S}\approx \mathcal{N}\left(\mathbf{T},\mathrm{\Omega }\right)$. To construct the temperature reconstruction covariance $\mathbf{\Omega }$, we assume $\mathbf{S}$ is an AR(1) time series, with variance as specified in the reconstruction and a correlation e-folding time of 10 y. For each iteration i of our MH algorithm, we draw $n=100$ samples ${\mathbf{T}}_j$ from $\mathbf{T}|\mathbf{S}$. We assume that $\mathbf{S}$ and $\mathbf{T}$ have uninformative priors, so that $P\left(\mathbf{T}|\mathbf{S}\right)=P\left(\mathbf{S}|\mathbf{T}\right)$. We then calculate the corresponding sea-level time series ${\mathbf{h}}_{i,j}=\mathbf{h}\left({\mathbf{\Psi }}_i,{\mathbf{T}}_j\right)$, which we compare with the reconstructed GSL $\mathbf{g}$ to calculate the posterior probability distribution $P\left({\mathbf{\Psi }}_i|\mathbf{g},\mathbf{S}\right)$,

$$\begin{array}{c}P\left({\mathbf{\Psi }}_i|\mathbf{g},\mathbf{S}\right)\approx P\left(\mathbf{g}|{\mathbf{\Psi }}_i,\mathbf{S}\right)P\left({\mathbf{\Psi }}_i|\mathbf{S}\right)\\ =P\left(\mathbf{g}|{\mathbf{\Psi }}_i,\mathbf{S}\right)P\left({\mathbf{\Psi }}_i\right)\\ \approx P\left(\mathbf{g}|{\mathbf{\Psi }}_i,\mathbf{T}\right)P\left(\mathbf{T}|\mathbf{S}\right)P\left({\mathbf{\Psi }}_i\right)\\ \approx \frac{1}{n}{\displaystyle \sum _{j=1}^{n}P\left(\mathbf{g}|{\mathbf{\Psi }}_i,{\mathbf{T}}_j\right)P\left({\mathbf{\Psi }}_i\right)}\end{array}$$ [12]

$$\begin{array}{c}P\left(\mathbf{g}|{\mathbf{\Psi }}_i,{\mathbf{T}}_j\right)={\left|2\pi \mathbf{\Sigma }\right|}^{-1/2}\\ \times \exp \left(-\frac{1}{2}{\left[\widehat{\mathbf{g}}-{\mathbf{h}}_{i,j}\right]}^{\mathrm{\top }}{\mathbf{\Sigma }}^{-1}\left[\widehat{\mathbf{g}}-{\mathbf{h}}_{i,j}\right]\right)\end{array}$$ [13]

where $\mathbf{g}\approx N\left(\widehat{\mathbf{g}},\mathbf{\Sigma }\right)$ is taken from the ML_2,1 reconstruction. To calculate the posterior distribution of the portion of GSL change explainable by the semiempirical model, we simply take the distribution of ${\mathbf{h}}_{i,j}$. The prior and posterior distributions of $\mathbf{\Psi }$ are shown in Dataset S1, j.

To balance skill in modeling GSL with skill modeling the rate of change of GSL, we taper the original covariance matrix ${\mathbf{\Sigma }}_r$ estimated from the GP model. The resulting matrix $\mathbf{\Sigma }={\mathbf{\Sigma }}_r\circ \mathit{\lambda }$ is the entrywise product of the original matrix and an exponentially falling tapering function ${\lambda }_{i,j}=\exp \left(-\left|t_i-t_j\right|/{\tau }_{cov}\right)$. We select a value of ${\tau }_{cov}$ = 100 y, which is the maximum-likelihood estimate for the Mann et al. calibration based on a comparison of results for no tapering, a fully diagonal matrix, and values of ${\tau }_{cov}\in \left\{10,\hspace{0.17em}50,\hspace{0.17em}100,\hspace{0.17em}200,\hspace{0.17em}500,\hspace{0.17em}\mathrm{1,000}\right\}\hspace{0.17em}\text{y}$ (Fig. S5B).

Counterfactual hindcasts of 20th century GSL were calculated by substituting ${\mathbf{T}}_j^{\prime }$ for ${\mathbf{T}}_j$ in Eqs. 12 and 13, where each sample ${\mathbf{T}}_j$ was transformed into ${\mathbf{T}}_j\prime$ such that either (i) 20th century temperature followed a trend line fit to ${\mathbf{T}}_j$ from 500 CE to 1800 CE, or (ii) 20th century temperature was equal to the 500–1800 CE average of ${\mathbf{T}}_j$. The historical baseline ${\mathbf{T}}_j″$ was generated by replacing ${\mathbf{T}}_j$ after 1900 CE with HadCRUT3, shifted so as to minimize the misfit between HadCRUT3 and ${\mathbf{T}}_j$ over 1850–1900. The nonanthropogenic fraction is calculated as the distribution of $\mathbf{h}({\mathbf{\Psi }}_i,{\mathbf{T}}_j″)-\mathbf{h}\left({\mathbf{\Psi }}_i,{\mathbf{T}}_j\prime \right)$ (Fig. S4).

Projections of global mean temperature for the three RCPs were calculated using the simple climate model MAGICC6 (101) in probabilistic mode, similar to the approach of ref. 23. As described in ref. 102, the distribution of input parameters for MAGICC6 was constructed through a Bayesian analysis based upon historical observations (103, 104) and the equilibrium climate sensitivity probability distribution of AR5 (105). We combined every set of parameters ${\mathbf{\Psi }}_i$ and historical temperatures ${\mathbf{T}}_j$ with every single temperature realization of MAGICC6, so the uncertainties are a combination of parameter uncertainty, initial condition uncertainty, and projected temperature uncertainty.

Sensitivity Tests for Reconstruction

We consider five alternative empirical calibrations of the hyperparameters $\mathbf{\Theta }=\left\{{\sigma }_g,{\sigma }_l,{\sigma }_m,{\sigma }_w,{\sigma }_0,{\sigma }_{g0},{\tau }_g,{\tau }_m,{\lambda }_l,{\lambda }_m\right\}$ (Dataset S1, c, and Fig. S3). (i) For prior ML_2,2, $\mathbf{\Theta }$ is empirically calibrated through a hybrid global simulated annealing/local sequential quadratic programming optimization to find the hyperparameters that maximize the likelihood of the model conditional upon the observations. (ii) Prior ML_2,1 is similar to prior ML_2,2, but with the constraint that ${\tau }_m={\tau }_g$, i.e., that there is one timescale hyperparameter for the nonlinear terms. (iii) Prior ML_1,1 is similar to prior ML_2,2, but with the constraints that ${\tau }_m={\tau }_g$ and ${\sigma }_m={\sigma }_g$, i.e., that there is one timescale hyperparameter and one amplitude hyperparameter for the nonlinear terms. (iv) For prior NC, ${\sigma }_g$ and ${\tau }_g$ are optimized to maximize the likelihood of a GP model fit to the curve derived from the detrended North Carolina RSL reconstruction. The remaining hyperparameters are then empirically optimized to maximize the likelihood of the model conditional upon the observations. (v) For prior Gr, ${\sigma }_g$ and ${\tau }_g$ are optimized to maximize the likelihood of a GP model fit to the ref. 20 GSL hindcast. The remaining hyperparameters are then empirically optimized to maximize the likelihood of the model conditional upon the observations.

In all cases, the parameters were optimized conditional only upon observations with $2\sigma$ age uncertainties of less than $\pm 50$ years. In order to ensure that the optimization process does not confuse the interpretations of the terms reflecting the processes of interest and the white-noise term, we optimized under the constraint that τ_g and τ_m > 100 y. To ensure that this is a reasonable constraint, we also tested a model in which the amplitude of the global term, σ_g, was set equal to zero; thus, in this model, all observations were interpreted as reflecting regional changes. Without the inclusion of the global term, the optimal value of τ_m is 123 y, consistent with the constraint.

From an interpretive perspective, the main difference among the calibrated prior is the timescale of GSL variability ${\tau }_g$ (Dataset S1, c). In priors ML_2,1 and ML_1,1, this timescale is $\sim 100$ y, whereas, for ML_2,2, it is ∼2,000 y, yielding an overly smooth GSL curve; other priors have intermediate timescales. Shorter timescales lead a greater proportion of centennial-scale variability to be attributed to GSL. Although ML_2,2 has the highest marginal likelihood, we focus on ML_2,1 in presenting results, as inspection of within-20th century rate estimates for ML_2,2 suggests oversmoothing. Prior estimates of rates and variability are shown in Dataset S1, d.

We also consider the application of the model with the ML_2,1 before different subsets of data (Dataset S1, f). The decline in GSL between 1000 CE and 1400 CE is robust to the removal of North Atlantic data ($P=0.91$ in subset -NAtlantic+GSL) and to the consideration only of data from the Atlantic and the Mediterranean ($P=1.00$ in subset +AtlanticMediterranean+GSL). It is, however, not robust to the consideration only of data from South America ($P=0.48$ in subset +SAmerica+GSL) or only of data outside the Atlantic and Mediterranean ($P=0.25$ in subset -AtlanticMediterranean+GSL).

To assess the impact of the exogenous ref. 12 GSL curve for the 20th century, we consider each subset of data with and without the inclusion of this curve (indicated in Dataset S1, f by +GSL and -GSL). Twentieth century rates have broader errors without the exogenous 20th century curve but are in general agreement with that curve (e.g., +All+GSL: $1.38\pm 0.15$ mm/y; +All-GSL: $1.31\pm 0.33$ mm/y).