Figure 8.

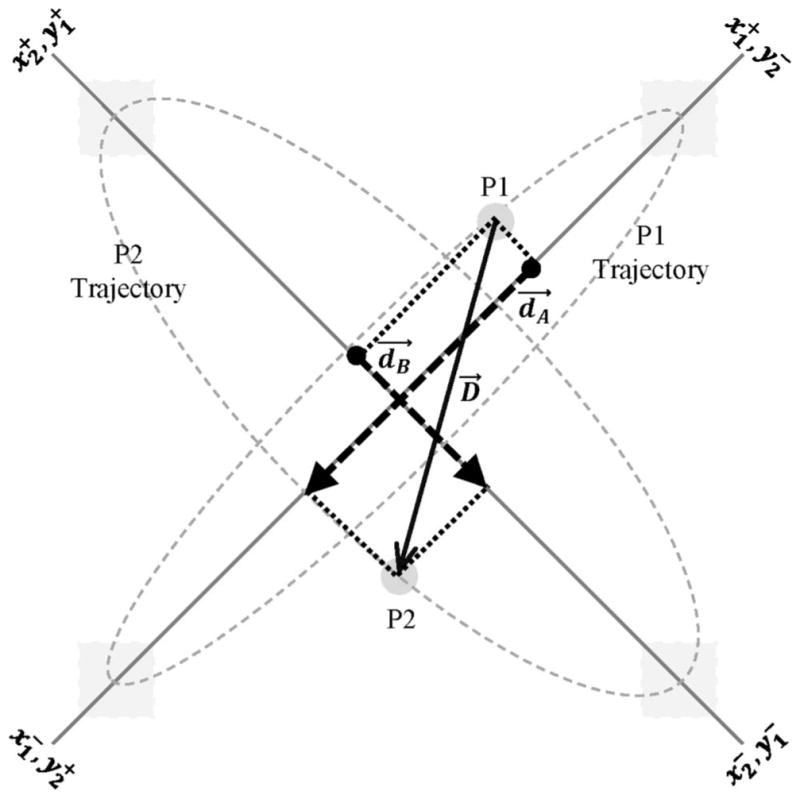
Illustration of how the displacement vector between participants’ on-screen end-effector locations is projected onto the appropriate task-dynamic axes for defining the repeller coupling functions in Equations 4a–d. The target locations (gray squares) are located at the corners of the screen. The solid gray lines along the screen’s intertarget diagonals represent the primary (limit cycle) task-space motion axes (x₁ and x₂) and orthogonal (point-attractor) motion axes (y₁ and y₂) of the participants, P₁ and P₂. The task axes of P₁ are rotated CCW 45° from the screen’s right-horizontal axis, and the task axes of P₂ are rotated CCW 135° from the screen’s right-horizontal axis; thus, the labels ${\mathit{x}}_{\mathit{i}}^{+}$ and ${\mathit{y}}_{\mathit{i}}^{+}$ at the ends of the intertarget on-screen diagonals denote the positive-going directions for motions along the corresponding x_i and y_i axes of the ith participant. The gray dashed lines reflect idealized on-screen movement trajectories of the participants, with the gray disks representing the current on-screen locations of P₁ and P₂ along these movement trajectories. In this example, the solid black line with open arrow heads, D, is the displacement vector from P₁ to P₂, and the dashed black lines with closed arrow heads, d_A and d_B, represent the projections of D onto the relevant task axes of P₂, that is, d_A = y₂ − (− x₁) = y₂ + x₁ as in Eq. 4d, and d_B = x₂ − y₁ as in Equation 4b. Note that the displacement vector from P₂ to P₁ would be represented by −D, and its projections onto the task axes of P₁ would be defined by −d_A = x₁ − (− y₂) = x₁ + y₂ as in Eq. 4a and −d_B = y₁ − x₂ as in Eq. 4c.