Finite Element Simulation of Articular Contact Mechanics with Quadratic Tetrahedral Elements

Abstract

Although it is easier to generate finite element discretizations with tetrahedral elements, trilinear hexahedral (HEX8) elements are more often used in simulations of articular contact mechanics. This is due to numerical shortcomings of linear tetrahedral (TET4) elements, limited availability of quadratic tetrahedron elements in combination with effective contact algorithms, and the perceived increased computational expense of quadratic finite elements. In this study we implemented both ten-node (TET10) and fifteen-node (TET15) quadratic tetrahedral elements in FEBio (www.febio.org) and compared their accuracy, robustness in terms of convergence behavior and computational cost for simulations relevant to articular contact mechanics. Suitable volume integration and surface integration rules were determined by comparing the results of several benchmark contact problems. The results demonstrated that the surface integration rule used to evaluate the contact integrals for quadratic elements affected both convergence behavior and accuracy of predicted stresses. The computational expense and robustness of both quadratic tetrahedral formulations compared favorably to the HEX8 models. Of note, the TET15 element demonstrated superior convergence behavior and lower computational cost than both the TET10 and HEX8 elements for meshes with similar numbers of degrees of freedom in the contact problems that we examined. Finally, the excellent accuracy and relative efficiency of these quadratic tetrahedral elements was illustrated by comparing their predictions with those for a HEX8 mesh for simulation of articular contact in a fully validated model of the hip. These results demonstrate that TET10 and TET15 elements provide viable alternatives to HEX8 elements for simulation of articular contact mechanics.

INTRODUCTION

Advances in imaging and computational methods make it possible to create and analyze detailed subject-specific models of biomechanical structures from high resolution image data. In this paper we focus on subject-specific finite element (FE) analysis of articular joint contact mechanics. Both generic and subject-specific models of articular contact have been developed and validated to gain insight into load transfer, cartilage mechanics and the etiology of osteoarthritis in the knee (Khoshgoftar et al., 2015; Luczkiewicz et al., 2015), hip (Harris et al., 2012; Henak et al., 2014) ankle (Anderson et al., 2007; Kern and Anderson, 2015) and spine (Dreischarf et al., 2014; Von Forell et al., 2015), among other joints. Despite the progress that has been made in modeling subject-specific joint contact mechanics, many challenges still remain. The articular cartilage of most joints in the human body has complex geometry, undergoes large deformations, is subjected to large compressive loads, and is often thin compared to the surrounding anatomical support. These challenges make it difficult to obtain accurate, validated computational models of articular contact mechanics.

The element type used to discretize the articular geometry is one of the most important choices that affects accuracy and robustness in simulations of articular contact. Linear tetrahedral (TET4) elements are often used due to the ease and robustness of performing automatic meshing, and local and adaptive refinement with tetrahedral elements (Hubsch et al., 1995; Johnson and MacLeod, 1998; Prakash and Ethier, 2001; Spilker et al., 1992) (Delaunay, 1934; Lo, 1991a, b; Lohner, 1996; McErlain et al., 2011; Shephard and Georges, 1991; Wrazidlo et al., 1991). There are several examples in the recent literature that have used TET4 elements to discretize articular cartilage (Das Neves Borges et al., 2014; Johnson et al., 2014; McErlain et al., 2011). However, the TET4 element has several well-known numerical issues. First, TET4 elements can only represent a constant strain state, which necessitates a very fine discretization, often requiring long solution times. Second, TET4 elements lock for nearly incompressible materials as well as under bending deformations (Hughes, 2000), which further reduces their accuracy. Because of these issues, trilinear hexahedral elements (HEX8) have seen much wider use in joint contact analyses, despite the fact that creating hexahedral meshes for complex geometries can be challenging and time consuming. Alternative formulations for TET4 elements have been designed to circumvent their problems (e.g., (Gee et al., 2009; Puso and Solberg, 2006) based on nodal averaging of the deformation gradient). Although they reduce locking, they have other problems such us spurious deformation modes (Maas, 2011), which make them inaccurate for contact analysis.

Quadratic tetrahedral elements are an attractive alternative to TET4 elements. They maintain the advantages of tetrahedral mesh generation and they can represent curved boundaries more accurately than HEX8 elements since their edges and faces can deform. Although quadratic tetrahedral elements have been investigated as alternatives to HEX8 elements (e.g., (Cifuentes and Kalbag, 1992; Tadepalli et al., 2011; Weingarten, 1994)), none of these studies investigated their application for simulation of articular contact analyses. The 10-node tetrahedron (TET10) has seen some limited use for contact mechanics (Bunbar et al., 2001; Hao et al., 2011; Tadepalli et al., 2011; Wan et al., 2013; Yang and Spilker, 2006). To our knowledge the 15-node tetrahedron (TET15) has never been used in computational biomechanics and it has seen very limited use in nonlinear computational solid mechanics at all (Danielson, 2014), although it has been used in the fluid mechanics community (Bertrand et al., 1992).

The objectives of this study were to determine the efficacy in terms of accuracy of the recovered stresses, robustness in terms of the convergence behavior, and computational expense of the TET10 and TET15 elements compared to the HEX8 element in the context of articular contact mechanics. First, the effects of different integration rules on the stress predictions and computational cost were investigated and used to determine suitable integration rules for both the TET10 and TET15 elements. Then using these integration rules, the accuracy and computational cost of both elements were compared to the HEX8 element for several benchmark contact problems. For one of these problems, we examined the results obtained using TET4 elements to contrast their performance with the quadratic elements. Finally, we compared predictions of contact stresses using HEX8, TET10, and TET15 elements for a validated model of hip contact mechanics (Henak et al., 2014).

METHODS

Element formulation and numerical integration

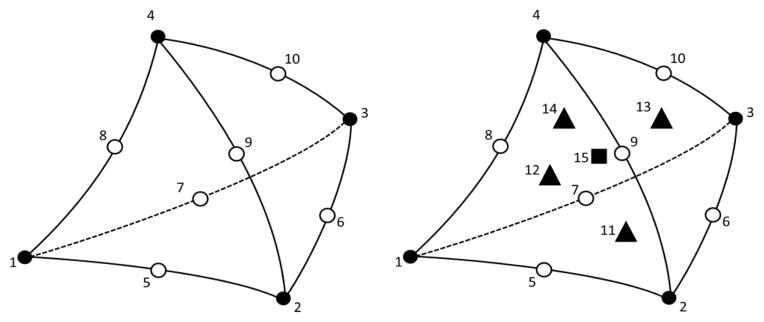
All element formulations in this research were implemented in the FEBio software suite (www.febio.org), which uses an implicit, Newton-based method to solve the nonlinear FE equations of solid mechanics (Maas et al., 2012a). The TET10 element has 10 nodes: 4 corner nodes and 6 nodes located at the midpoint of the edges (Figure 1). Due to the quadratic shape functions, the facets and edges of this element can distort and therefore the element behavior is “softer” than the TET4 element. The TET15 element adds one more node at the center of each facet, and one in the center of the tetrahedron (Figure 1). Although the TET15 element has more nodes than the TET10, it is still a quadratic element since the highest order of complete polynomial that can be represented by the shape functions is second order. The TET15 element can represent some forms of quadratic strains, whereas the TET10 element can only represent linear strains.

Figure 1.

Schematic of the node topology for two quadratic tetrahedral elements that were examined in this study. Left, 10-node quadratic tetrahedron (TET10). Right, 15-node quadratic tetrahedron (TET15). Closed circles represent corner nodes, open circles represent edge nodes, triangles represent facet center nodes, and the square in the right image represents the center node of the TET15 element.

In a FE formulation, the discretized form of the equilibrium equations requires the use of appropriate numerical integration schemes. For second-order elements, the integration rule should have at least second-order accuracy, at least for linear analyses. The ideal integration rule is less clear for large deformation nonlinear analyses. For this reason, we implemented and compared several volumetric integration rules. We denote volume integration rules as V(n) where (n) indicates the number of integration points. Similarly, the notation S(n) is used to denote surface integration rules. For the TET10 element, both 4-point (V4) and 8-point (V8) Gauss integration rules were implemented (Abramowitz and Stegun, 1964). For the TET15 element, 11-point (V11) and 15-point (V15) Gauss integration rules were implemented (Keast, 1986). All of these rules are at least second-order accurate (for linear analyses) and are symmetric, i.e. the integration points are distributed in a symmetrical spatial pattern.

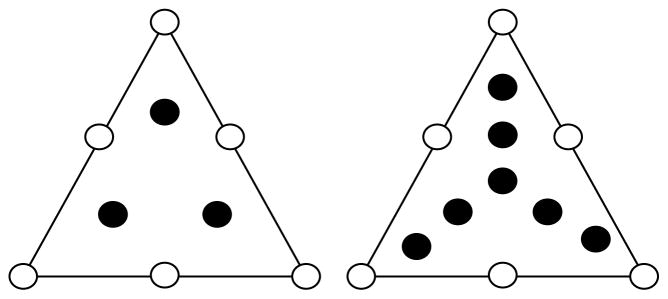
For contact enforcement, a surface integration rule is required to integrate the traction forces over the discrete surface, represented by facets of the finite elements. The facets of the TET10 element are 6-node quadratic triangles. Two surface integration rules were implemented and compared: 3-point Gauss (S3), and 7-point Gauss (S7) (Figure 2). For the TET15 element, a 7-node quadratic facet, and the same S3 and S7 integration rules were implemented. Again, these rules have at least second-order accuracy and are symmetric (Abramowitz and Stegun, 1964).

Figure 2.

Schematic of the surface integration rules that were implemented and tested for evaluation of the contact integrals for the quadratic triangle facets composing the surface of the tetrahedral elements. Left panel: S3 integration rule. Right panel: S7 integration rule. Open circles represent nodes, filled circles represent integration points. Note that these integration rules are symmetric in spatial distribution.

The mean dilatation formulation was used for the HEX8 models (Simo and Taylor, 1991). This formulation is known to perform well for nearly-incompressible materials for which the standard displacement-based formulation, using full integration, has a tendency to lock.

All analyses were performed using the quasi-Newton solver in FEBio (Maas et al., 2012b), which is based on the Broyden-Fletcher-Goldfarb-Shanno (BFGS) method (Matthies and Strang, 1979). This nonlinear solver begins with a full formation and factorization of the stiffness matrix and then proceeds with a user-defined number of BFGS updates, which involve computation of the right-hand-side (RHS) vector. For two of the problems below, we report both the number of stiffness matrix reformations and RHS evaluations as metrics of nonlinear convergence and computational effort. All contact analyses used the “sliding-tension-compression” contact algorithm in FEBio (Maas et al., 2012b). This algorithm implements a facet-on-facet, frictionless sliding contact where the contacting surfaces can separate but not penetrate (Laursen, 2002). The augmented Lagrangian method was used to enforce the contact constraint to a user-defined tolerance (Laursen and Maker, 1995).

Stress recovery

During the FE solution process, stresses are typically evaluated at the integration points. Since stresses are calculated using the shape function derivatives, they are usually discontinuous across element boundaries. For visualization and for further postprocessing analysis (e.g. a-posteriori stress error estimates (Zienkiewicz and Zhu, 1992)), a more accurate, continuous stress field is required. This is accomplished using a stress-recovery algorithm that projects the stresses from the integration points to the nodes. For TET4 elements, a weighed nodal average of the surrounding element values is usually sufficient, but for quadratic elements this does not produce good results. We implemented and used the Superconvergent Patch Recovery (SPR) method to recover stresses for the quadratic elements (Zienkiewicz and Zhu, 1992). This method incorporates a least-squares approach to fit a polynomial to the integration point values of an element patch surrounding each node. The polynomial is then evaluated at the nodes to determine the nodal value. Another important reason for investigating different integration rules is to determine the minimal integration rule that recovers the stresses accurately. Since the SPR method uses least-squares, each node must be surrounded by a minimal number of integration points to solve the least-squares system. This could pose problems at the boundary of the mesh and in thin structures. For the TET10 element, we used a linear least-squares fit since there are often not enough integration points (especially for the V4 integration rule) to fit a complete quadratic polynomial. For the TET15 element, a complete quadratic polynomial was used.

Plane strain contact

Different combinations of surface and volume integration rules were investigated using a plane strain contact model (Figure 3). This model is representative of articular contact mechanics in that it models the contact between curved, thin, incongruent, deformable materials. The model consisted of two parts. The top part had dimensions of 1.5 mm (height)×20 mm (length)×1 mm (thickness). The bottom part had the same height and thickness but was curved downward with a radius of curvature of 58 mm. The bottom of the curved layer was fixed while the top of the flat layer was displaced downward. Since FEBio is designed for 3D analysis, plane strain boundary conditions were created by preventing the nodes from displacing in the out-of-plane direction. The materials of both layers were represented by an uncoupled Mooney-Rivlin constitutive model with strain energy:

$$W_{MR}=c_1\left({\stackrel{\sim }{I}}_1-3\right)+c_2\left({\stackrel{\sim }{I}}_2-3\right)+\frac{1}{2}k{\left(lnJ\right)}^2.$$ (1)

Figure 3.

Schematic of the plane strain contact problem. The bottom surface of the curved layer is held fixed, while the top layer undergoes a prescribed downward displacement. Dashed area shows the region illustrated in the contour plots in Figure 5.

Here, Ĩ₁, Ĩ₂ are the first and second invariants of the deviatoric right Cauchy-Green deformation tensor, and J is the determinant of the deformation gradient. This material formulation and the material coefficients below were chosen to represent articular and femoral articular cartilage and coincide with the properties of a validated hip joint model (discussed below). The material parameters were c₁ = 2.98 MPa, c₂ = 0 MPa, k = 594 MPa, for the flat layer; and c₁ = 1.86 MPa, c₂ = 0 MPa, k = 371 MPa for the curved layer. To compare the integration rules, we examined isovalue fringe plots of the 3^rd principal stress and searched for erroneous patterns in the isovalues.

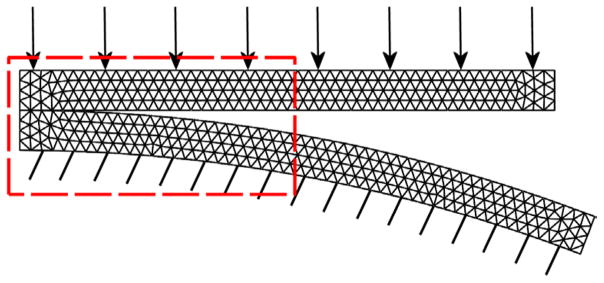
Compression and sliding of a rigid cylinder on a deformable block

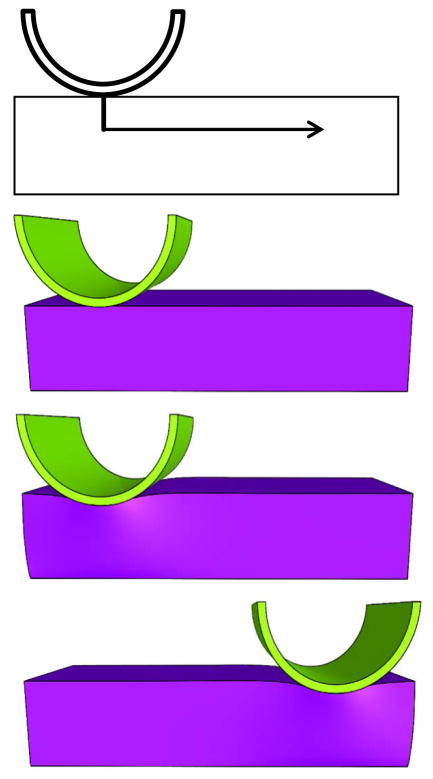
To assess the performance of the quadratic tetrahedral elements in contact problems with large amounts of sliding, a benchmark problem from the FEBio Verification Suite was used (co07.feb). This is a revelant test problem since many joints (e.g. knee, shoulder, hip) undergo large amounts of sliding during articular contact. A rigid cylinder (outer radius = 1 mm) first indents a rectangular block (length = 5 mm, width = 1.9 mm, height = 1 mm) and then slides across the surface of the block (Figure 4). The cylinder was modeled as a rigid body using quadratic 20-node hexahedral elements. Mid-side nodes of the elements were positioned so that the surface of the cylinder was smooth to avoid jumps in the contact stiffness due to discontinuities in the surface normal. Again, as before, the material formulation was chosen to represent articular cartilage. The rectangular block was represented using the Mooney-Rivlin model above (c₁ = 2.98 MPa, c₂ = 0 MPa, k = 594 MPa) and was discretized with TET4, TET10 and TET15 elements. A model using HEX8 elements was created and used as a reference. A mesh convergence study was conducted to allow fair assessment of the computational costs of the four element types (Table 1). Convergence was measured in terms of average reaction force on the rigid indenter over the entire horizontal displacement of the indenter. Fringe plots of the 3^rd principal stress at the midpoint of the analysis were used to compare the predictions of the models.

Figure 4.

Geometry and loading path of the rigid cylinder on the deformable box. First, the cylinder was displaced vertically. After reaching maximal vertical displacement, a horizontal displacement was applied while the vertical position was maintained. From top to bottom: schematic diagram, initial configuration, configuration at maximal vertical displacement, final configuration.

Table 1.

Results of the mesh convergence study for the contact sliding problem showing the number of nodes and elements, the number of time steps to complete the analysis, the number of matrix reformations (Refs) and right-hand side (RHS) evaluations, and runtime in seconds, the average reaction force during horizontal displacement of the indenter, estimated contact area and peak contact pressure at midpoint of horizontal displacement.

HEX8	Nodes	Elements	Steps	Refs.	RHS	Time (sec)	Force (kN)	Contact Area (mm2)	Peak Contact Stress (MPa)
Mesh1	2366	1800	40	79	995	53	4.82	1.6	−4.3
Mesh2	5208	4200	40	86	989	137	4.80	1.5	−4.7
Mesh3	9471	8000	40	84	1039	305	4.77	1.4	−4.7
Mesh4	17136	15000	40	84	1131	707	4.75	1.4	−4.8
Mesh5	33306	30000	40	88	1136	1931	4.76	1.4	−4.8
TET4
Mesh1	2392	9524	40	109	1237	40	8.06	1.2	−6
Mesh2	5237	23259	40	84	1075	91	6.79	1.2	−7
Mesh3	9464	44049	40	82	1097	205	6.18	1.2	−6
Mesh4	17158	85561	40	87	1150	533	5.71	1.2	−7
Mesh5	33477	175945	41	98	1259	1785	5.38	1.2	−6
TET10
Mesh1	2364	1128	40	93	1068	34	5.07	1.6	−4.7
Mesh2	5243	2824	40	81	1049	88	4.89	1.6	−5.2
Mesh3	9487	5521	40	82	1073	211	4.83	1.6	−5.0
Mesh4	17162	10331	40	90	1150	545	4.80	1.5	−5.4
Mesh5	33350	21049	42	99	1266	1748	4.78	1.5	−5.2
TET15
Mesh1	2299	389	40	94	1155	27	5.35	1.7	−5.1
Mesh2	5521	999	40	87	1068	77	4.94	1.7	−5.2
Mesh3	9459	1815	40	83	1053	151	4.86	1.6	−5.2
Mesh4	17033	3383	40	83	1058	332	4.82	1.5	−5.3
Mesh5	33023	6694	40	84	1100	864	4.79	1.5	−5.2

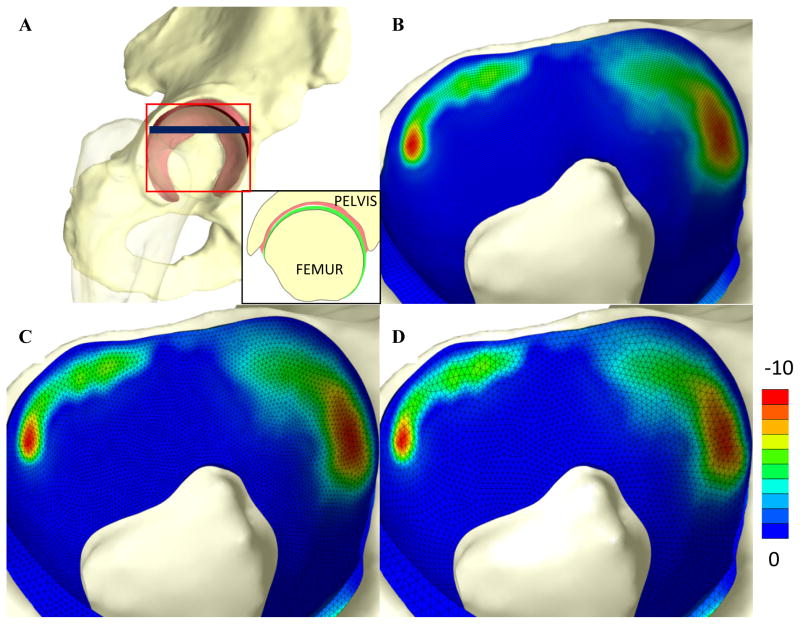
Articular contact in the human hip

To test the effectiveness of quadratic tetrahedral elements for production size articular contact problems involving complex geometry, the articular layers in a model of the hip from a previous validation study (Henak et al., 2014) were discretized with tetrahedral elements (Figure 9). In this previous study, articular layers were discretized with HEX8 elements and after a mesh convergence study it was determined that six elements through the thickness produced converged results. The thickness varied across the articular surfaces and ranged from 0.2 mm to 3.7 mm on the femoral side and from 0.5 mm to 4.5 mm on the acetabular side. The HEX8 model was validated with experimental measurements of contact stress. Cartilage layers were modeled using a Mooney-Rivlin material (acetabular cartilage c₁=2.98 MPa, c₂=0 MPa, k=594 MPa, femoral cartilage c₁=1.86 MPa, c₂=0 MPa, k=371 MPa). For this study, two additional models were created using TET10 and TET15 elements. The mesh resolution was chosen such that the number of nodes (and thus the degrees of freedom) roughly matched the HEX8 model (Table 2). For the tetrahedral models the number of elements through the thickness varied from one to four depending on the cartilage thickness. In the areas where contact was occurring there were about two to three elements through the thickness on average. Loading conditions were applied that simulated walking heel strike (Bergmann et al., 2001). A prescribed load of 1650 N was applied to the femur while keeping the pelvis fixed. The 3^rd principal stress, an indicator of contact stress, and contact area were compared.

Figure 9.

A) Finite element model of the human hip, including the acetabulum, proximal femur and articular layers on the acetabulum and femoral head. Red square shows approximate area corresponding to contour plots. Blue line shows approximate location of inset, showing cross-section of model B–D) Fringe plots of 3rd principal stress for the acetabular cartilage discretized with B) HEX8 elements, C) TET10 elements, and D) TET15 elements. There was very good agreement between the 3rd principal stress and contact area predicted by the three models.

Table 2.

Result of the hip model study where the results of a validated HEX8 model were compared with the predictions of a TET10 and TET15 model. The table lists the number of nodes and elements, peak contact stress, the contact area, the number of right-hand-side (RHS) evaluations, the number of stiffness reformations and the overall runtime (in minutes) for each of the three models.

	Nodes	Elements	Peak Contact Stress (MPa)	Contact Area (mm2)	RHS Evals	Reforms.	Run Time (min)
HEX8	144886	122148	−9.99	793	726	69	320
TET10	138081	83698	−9.93	792	892	80	374
TET15	139187	27905	−10.0	819	939	82	335

RESULTS

Plane strain contact

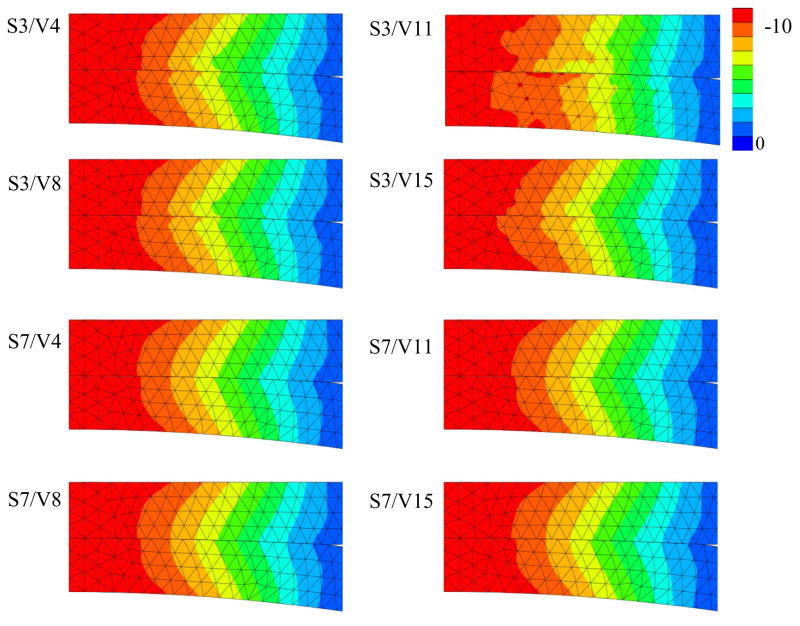
The surface integration rule had a large effect on predictions of 3^rd principal stress (Figure 5). The S3 surface integration rule predicted overall larger variations in stress near the contact interface than the S7 rule (compare rows 2 and 3 in Figure 5). We concluded that the S7 surface integration rule is the best choice of the two rules. In contrast, there was little effect of volume integration rule on predicted stresses (compare rows 3 and 4 in Figure 5). Indeed, comparing for instance the combination S3/V4 with S3/V8 for the TET10 element (Figure 5, left column), the results are nearly indistinguishable. A noticeable exception is the combination S3/V11 and S3/V15 for the TET15 element where the stresses do show a significant difference. We found that the combination S3/V11 ran very poorly and we suspect that this combination is unstable and should be avoided. Although the other results show little variation for the different volume integration rules, we did observe improved convergence behavior for the higher-order volume integration rules. For this reason the remaining simulations were done with the S7/V8 rule for the TET10 element and the S7/V15 for the TET15 element.

Figure 5.

Results for the plane strain contact problem. The isovalue fringe plots show 3rd principal stress for various combinations of surface and volume integration rules. Left column: results for TET10 element. Right column: results for the TET15 element. The first abbreviation in each label refers to the surface integration rule (S3, S7), while the second abbreviation refers to the volume integration rule (V4, V8, V11, V15). Overall, the S7 surface integration rule predicted more accurate stresses than the S3 rule. The volume integration rule did not have a significant effect on the predictions (with the combination S3/V11 a notable exception).

Compression and sliding of a rigid cylinder on a deformable block

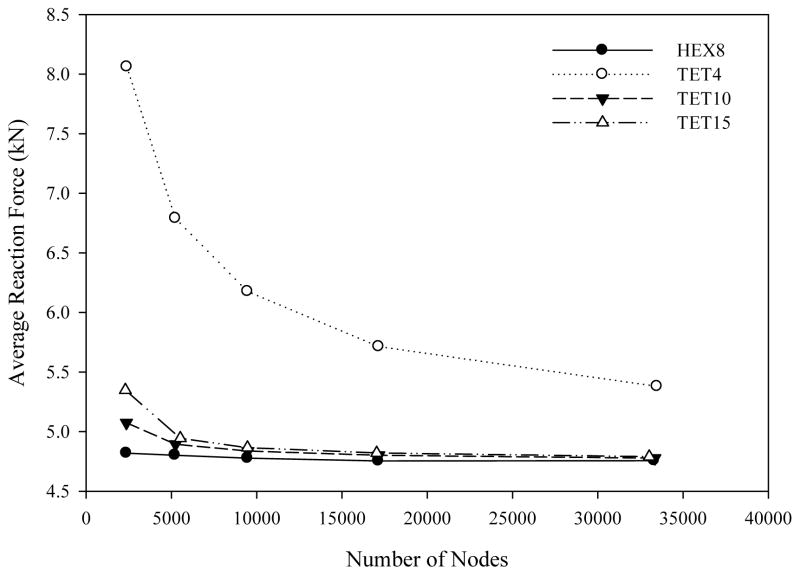
Overall reaction force on the cylinder provided an integrated measure of mesh convergence (Figure 6). The quadratic tetrahedral element formulations demonstrated excellent agreement above 10,000 nodes with the HEX8 results. With the exception of the coarsest meshes, all values are within one percent of each other (Table 1, far right column). This is in stark contrast with the TET4 results, which did not appear converged even at the finest resolution and predicted much larger reaction forces.

Figure 6.

Average reaction force on the rigid indenter while the indenter slides horizontally across the block, maintaining maximal vertical displacement. Average reaction forces are shown as a function of the number of nodes for a TET4 mesh, a TET10 mesh, a TET15 mesh and a HEX8 mesh. The TET10 and TET15 meshes above approximately 10,000 nodes are within 1% of the HEX results. The TET4 results predicted overall larger reaction forces and are not converged even at the finest mesh resolution.

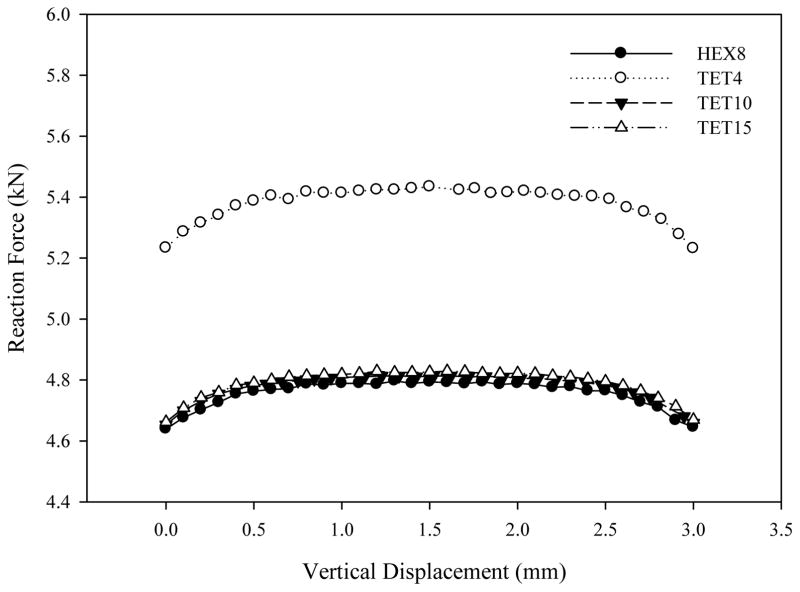
Inspecting the reaction force as a function of horizontal displacement can give an indication of the sensitivity of the reaction force to the mesh distribution. At the lowest mesh resolution all formulations showed fluctuations in the reaction forces, however at the finest resolution the reaction force varied smoothly (Figure 7). The difference between the minimum and maximum value was about 3% for each element formulation. The differences between the HEX8, TET10, and TET15 element formulations at a given displacement were even smaller and were less than 1%. Note again that the TET4 model predicted signifcantly larger reaction forces than the other three formulations.

Figure 7.

Variation of the reaction force on the rigid indenter as a function of horizontal displacement for the finest mesh resolution of HEX8, TET4, TET10, and TET15 models. The variation is relatively small and smooth throughout the entire displacement and is reduced at the start and end by boundary effects. The HEX8, TET10, and TET15 predicted overall the same response, whereas the TET4 predicted much higher reaction forces due to the stiffer response that results from the spatially constant interpolation of strain.

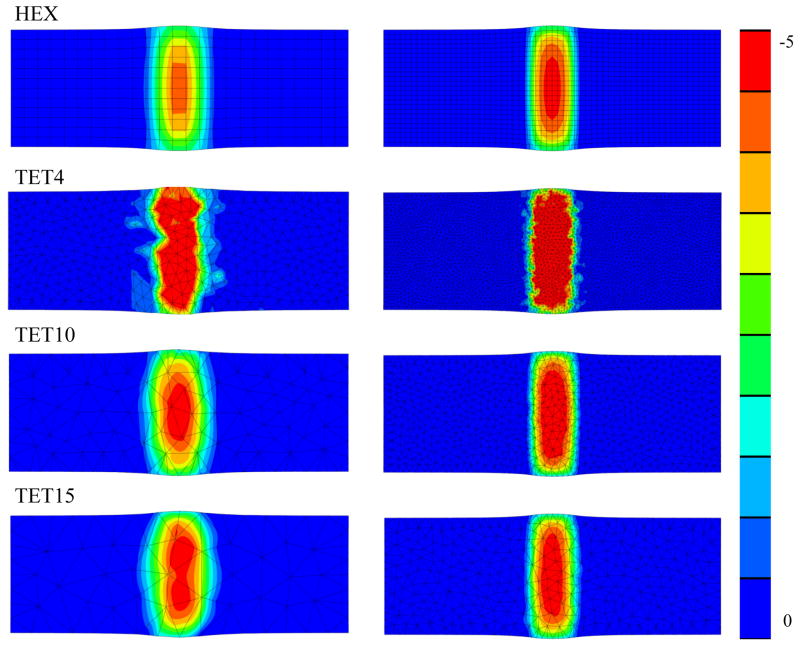
Converence behavior was comparable between the four element formulations. The number of stiffness matrix reformations and right-hand side evaluations were similar. The run times for the HEX8 were similar, though consistently higher, than those for the TET4 and TET10 formulations. The TET15 models ran sigfnicantly faster. The predicted 3^rd principal stress compared well between the quadratic tetrahedral and hexahedral models at the finest mesh resolutions (Figure 8, right column). For the coarsest mesh resolutions, the TET15 and TET10 models were similar to the HEX8 results, though variations due to the irregularity of the mesh were noticeable (Figure 8). The TET4 results were significantly higher and showed mesh dependent variations at all mesh resolutions.

Figure 8.

3^rd principal stress fringe plots for two different mesh densities at the half-way point of horizontal displacement. From left to right: coarsest mesh, finest mesh density. From top to bottom: HEX8, TET4, TET10, and TET15 mesh. Stress predictions were very similar for HEX8, TET10 and TET15 element formulations at the finest level (right column). The TET4 results were overall higher and did not appear to be smooth even at the finest level of refinement.

Articular Contact in the Hip

Based on the results of the previous two models, the S7 surface integration rule was used to evaluate the contact integrals for both tetrahedral elements in this model. The V8 and V15 volume integration rules were used for the TET10 and TET15 elements, respectively. There was good qualitative agreement of the contact stress (measured by the 3^rd principal stress) between the three models (Figure 9). Quantitative comparisons confirmed this observation. For both the TET10 and TET15 models, the peak contact stress and the contact area on the acetabular cartilage compared well to the HEX8 results (Table 2).

In terms of performance, measured by the convergence statistics as well as overall runtime, all three models ran comparably, although the TET10 model did run slightly longer than both the HEX8 and TET15 models (Table 2).

DISCUSSION

The results of this study demonstrate that quadratic tetrahedral elements are comparable both in computational cost and accuracy to the “gold standard” HEX8 elements for articular contact analysis. In some cases the TET15 models ran faster than the other models with comparable numbers of degrees of freedom, while in other cases they ran only slightly slower. It may seem surprising that these elements with more degrees of freedom are competitive in terms of computational cost, and in fact are faster than the TET4 model (e.g. the sliding contact example). Although the evaluation of the element quantities (i.e. element residual vector and stiffness matrix) is faster for low-order elements, the overall computational time may not follow the same pattern, as the examples clearly demonstrated. This can be explained by recognizing that many operations in the FE method (evaluation of global quantities, matrix assembly, etc.) are more proportional to the number of integration points than the number of degrees of freedom. This is especially true for contact problems, where the projection algorithm that determines the location of contact between surfaces can constitute a significant amount of the solution time. For a given number of nodes, a TET15 model will always have fewer elements than a similar TET10 or HEX8 and, although it uses more integration points than the TET10 or HEX8, the net sum often appears to be a reduction in the number of integration points. This may in part explain why the TET15 models ran faster in many cases.

The results of the plane strain contact analyses were very sensitive to the surface integration rule, and the S7 integration rule produced good results for the quadratic tetrahedrons. A possible explanation for this can be found by realizing that the accuracy of (Gaussian) integration rules is usually related to the ability to integrate polynomials exactly. For contact problems with non-conforming and possibly distorted surfaces, polynomials may not fit the surface tractions well and thus higher order integration rules are necessary to integrate the contact tractions accurately.

In contrast, the volume integration rule had little effect on the accuracy of the recovered stresses. All volume integration rules that were investigated are sufficient to obtain accurate results in linear analysis and it appears that, for the problems considered, the integration rules were also sufficiently accurate for nonlinear contact analysis. We did observe that the S3 surface integration rule in combination with the V11 volume integration rule for TET15 elements produced poor convergence as well as inaccurate results. We suspect that this combination does not lead to a stable element formulation. Despite the relatively small effect of the volume integration rule on the stress predictions, it may be prudent to consider the higher-order rules. The SPR recovery method, as with any least-squares method, requires a sufficient number of sample points to make the problem well-posed. In the present context this amounts to having a sufficient number of integration points surrounding each node. This may be challenging near boundaries, especially for articular contact problems, since the cartilage layers generally tend to be relatively thin. The result is that the V4 volume integration rule for TET10 prevents the use of a truly quadratic fit in the SPR recovery method. Although in this study we used a linear fit for the TET10 element and thus the V4 rule could have sufficed, there may be situations where the V8 rule is necessary to achieve accurate results. For the same reasons, for the TET15 elements, which contain additional monomials in their shape functions and thus require even more integration points that the TET10, it is prudent to consider the higher-order volume integration rule.

In this study we used “traditional” facet-on-facet based contact formulations (Laursen, 2002). In recent years, it has been demonstrated that mortar-based contact formulations have several advantages over traditional contact formulations (Puso et al., 2008). In essence, they minimize the error introduced by the non-conforming interface in either the displacements or the contact tractions. Yet, traditional formulations are widely used in many open-source and commercial finite element packages and thus evaluation of quadratic tetrahedral elements with traditional contact formulations has significant practical merit. These traditional formulations are known to give satisfactory results and, when used with an augmented Lagrangian method offer a good compromise between computational cost and accuracy. In addition, we anticipate that even for mortar-contact formulations the use of quadratic tetrahedral formulations will offer a distinctive advantage, foremost due their ability to represent arbitrarily curved surfaces more accurately than linear triangular elements. Thus, we expect that the findings in this study remain valid, regardless of the contact formulation, though further investigations are necessary to confirm this.

In this study we only looked at the effects of frictionless contact. This is not seen as a strong limitation since friction is usually not considered in articular contact. That said, friction is a feature that is still under development in FEBio’s contact formulations. Similarly, the effect of fluid motion in the tissue is of considerable interest in articular contact and was not considered here. The incorporation of fluid motion requires a biphasic analysis and the performance of quadratic tetrahedral formulations in this context is an important area for future investigation.

In the sliding contact case study we compared the quadratic tetrahedron results with linear tetrahedron results and demonstrated that, given the same number of nodes, the quadratic formulations, and especially the TET15 element, performed much better in all areas (i.e. accuracy, convergence, run-times) than the linear tetrahedron. In a way, this can be seen as yet another confirmation of the well-known mantra in finite element analysis that so-called p-refinement (i.e. increasing the polynomial order) is often a better refinement strategy than h-refinement (i.e. reducing the element size). Simply moving from a linear to a quadratic formulation resulted in vast improvements. In addition, the decreased run-times of higher-order tetrahedral formulations (for a given number of nodes), although perhaps surprising, is seen as an additional advantage of these quadratic tetrahedral formulations.

In conclusion, quadratic tetrahedral formulations offer an excellent alternative to HEX8 elements for simulation of articular contact. The TET15 element in particular appears to be very well suited for articular contact analysis.