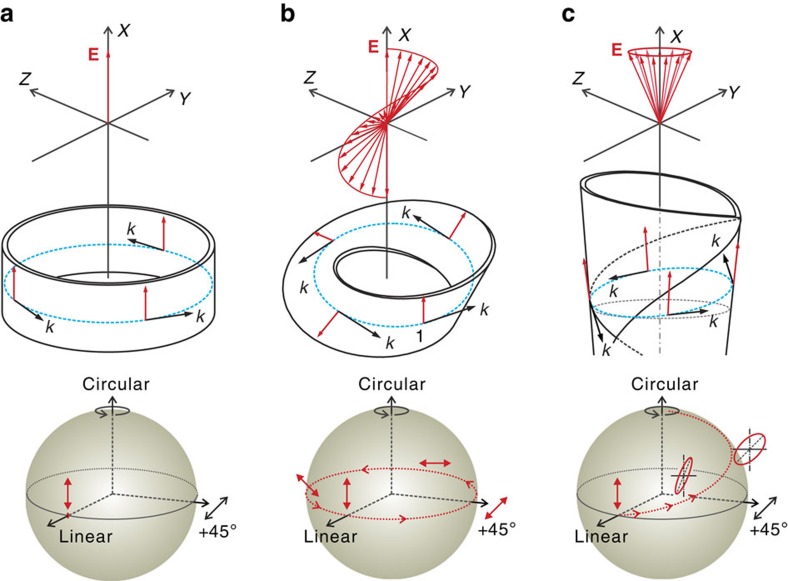
Figure 1. Optical spin–orbit coupling in WGM microcavities (top panel) and the corresponding polarization evolution on the Poincaré sphere (bottom panel).

(a) In-plane polarized light does not provide orbital angular momentum in a symmetric ring resonator due to the unchanged electric field (E) vector with respect to the wave vector k, which results in a stationary point on the Poincaré sphere. (b) In a Möbius-ring resonator, the twisted electric field E along the Möbius strip causes a varying orbital angular momentum for spin–orbit coupling, which results in a cyclic evolution on the Poincaré sphere. (c) An effective orbital angular momentum along X is generated due to the rotation of the major axis of the electric field E regulated by the cone-shaped tube wall of an anisotropic medium, allowing for an interaction with the spin angular momentum, which results in a non-cyclic evolution on the Poincaré sphere. The variations of the major polarization axis of the field E (red arrows) are shown with respect to the laboratory coordinate frame (XYZ). The blue dashed lines represent light trajectories, while the red dotted lines represent the polarization evolution trace on Poincaré sphere.