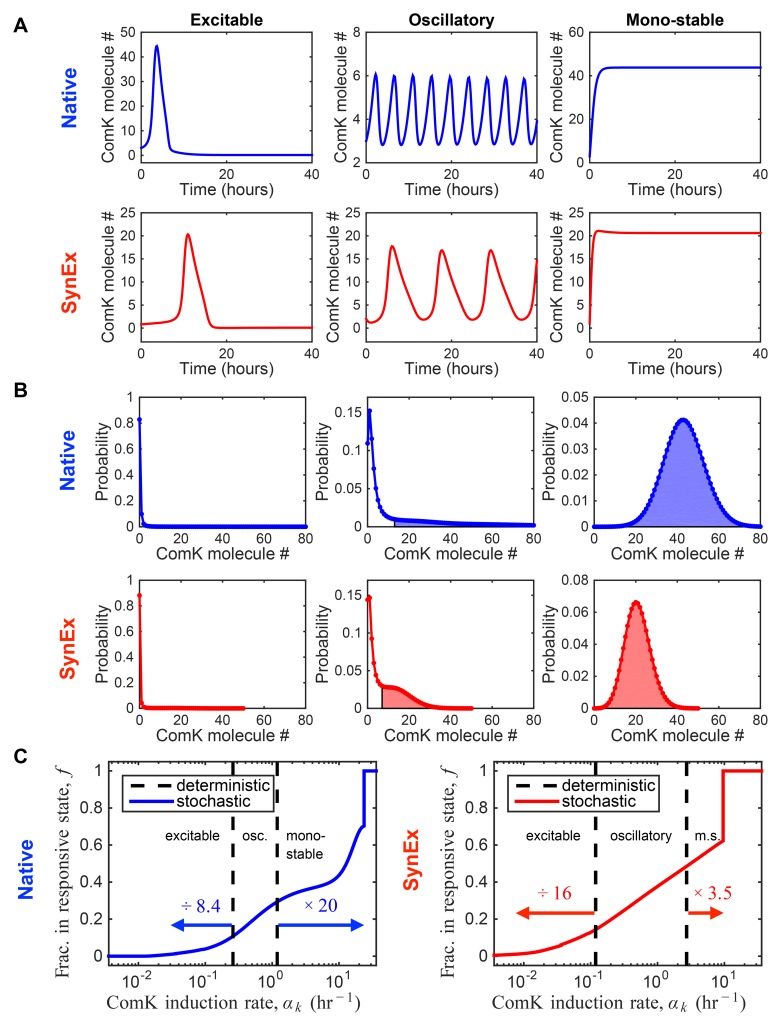
Fig 3. Stochastic modeling of B. subtilis competence.

(A) The deterministic model of each circuit (see Eqs 6 and 7) exhibits three dynamic regimes (excitable, oscillatory, and mono-stable), depending on the ComK induction rate α_k, which models stress level. (B) The stochastic model (see Eqs 1–5) reveals the ensuing distribution of ComK levels in each of the three dynamic regimes (excitable, oscillatory, and mono-stable). The fraction of the distribution in the responsive state f (determined by the inflection points, see Materials and Methods) is shaded. (C) Whereas the deterministic model exhibits sharp transitions between the dynamic regimes (dashed lines), the stochastic model exhibits a continuous dependence of f on induction rate. We see that for both circuits, stochasticity extends the viable response range (0 < f < 1) beyond the transitions predicted by the deterministic model, in both directions, by the factors given above the arrows (see Materials and Methods). Parameters are as in [16] and are given in S1 Text. In A and B, from left to right, the values of the control parameter are α_k = {0.072, 1.15, 36}/hour (native) and α_k = {0.036, 1.8, 36}/hour (SynEx). In A, from left to right, the initial conditions are ${\overline{n}}_0=\{3,3,3\}$ ComK molecules and ${\overline{m}}_0=\{15,5,0.1\}$ ComS molecules (native), and ${\overline{n}}_0=\{0.8,2,1\}$ ComK molecules and ${\overline{m}}_0=\{0.05,35,50\}$ MecA molecules (SynEx); in the excitable regime (left), the initial conditions are chosen to demonstrate the single, transient excitation.