Low levels of specularity support operational color constancy, particularly when surface and illumination geometry can be inferred

Abstract

We tested whether surface specularity alone supports operational color constancy – the ability to discriminate changes in illumination or reflectance. Observers viewed short animations of illuminant or reflectance changes in rendered scenes containing a single spherical surface, and were asked to classify the change. Performance improved with increasing specularity, as predicted from regularities in chromatic statistics. Peak performance was impaired by spatial rearrangements of image pixels that disrupted the perception of illuminated surfaces, but was maintained with increased surface complexity. The characteristic chromatic transformations that are available with non-zero specularity are useful for operational color constancy, particularly if accompanied by appropriate perceptual organisation.

1. INTRODUCTION

A. Overview

Specular highlights have long been recognized as a potential source of information about the color of the illumination on a scene[1, 2]. Here we test the influence of low levels of specularity on the perceptual separation of surface- and illuminant-contributions to the distal stimulus. When viewing a perfectly matte surface, obeying the Lambertian reflectance model, the spectral content of light reaching the eye is given by a wavelength-by-wavelength multiplication of the spectral content of the illuminant (I(λ)) and the spectral reflectance function of the surface (R(λ)). However, most surfaces are not completely matte and as well as reflecting the incident light modified by the spectral reflectance function of the surface (I(λ)R(λ)), they also reflect a proportion of the incident light that is, in the case of most non-metallic materials, not spectrally modified (I(λ)). These components are known respectively as the ‘diffuse’ or ‘body’ reflection and the ‘specular’ or ‘interface’ reflection [3]. The presence of a specular component usually results in the perception of gloss, although glossiness also depends on other factors in the image [4]. The diffuse and specular components differ in their geometry: The diffuse component is reflected isotropically, whilst the specular component is reflected in a direction determined by the angle of incidence, with additional deviations in reflectance angle introduced by the roughness of the surface. Such differences in geometry mean that the light reaching the eye from points across an object’s surface contains different additive mixtures of the diffuse and specular components. In the present study we ask whether the presence of even a weak specular component might allow observers to reliably classify image changes that arise from a change in surface reflectance versus those that arise from a change in the spectral content of the illuminant. We consider the chromatic statistics available, the systematic transformations of those chromaticities under illuminant and reflectance changes, and the spatial distribution of chromatic information across the image.

B. Color constancy

Human observers are described as color constant when their perception of object surface color depends only on the spectral reflectance of the surface and is unaffected by changes in the spectral content of the illuminant. The difficulty in achieving color constancy is that the spectral content of the light reaching the eye from the surface depends not only on the spectral reflectance function of the surface but also on the spectral content of the illuminant. Furthermore, the visual system does not have access to entire spectral functions, but only to the univariate outputs of the three cone classes (long-, middle-, and short-wavelength sensitive, L, M and S) in the retina. There are a number of models that suggest how the visual system might achieve approximate color constancy by implementing a color transformation whose parameters are set using chromatic statistics distributed over multiple surfaces in space and time (for review see [5-7]). An important result is that, for physically plausible reflectance functions and illuminant spectra, a change in illuminant imposes an approximately multiplicative scaling on the L-, M- and S-cone signals from a collection of surfaces [8-11], and the diagonal transform that corrects this scaling is the transform that maps the cone-coordinates of the second illuminant to the cone-coordinates of the first illuminant. Surfaces that produce specular reflections have been proposed as a source of information that could be used to set the parameters of a color constancy transform, since intense highlights have a chromaticity that is almost exactly that of the illuminant [1, 2]. However, at lower levels of specularity, the illuminant chromaticity will always be mixed with the chromaticity of the diffuse component. In this case it has been suggested that, when several glossy surfaces are present in a scene with a single illuminant, each surface will have a diffuse reflectance with chromaticity IR_i (where i = 1, 2, …n and n is the number of surfaces), and there will be several lines of samples in color space that converge at I. Even when the illuminant chromaticity is not directly available, this chromatic convergence [12] property may be used by the visual system to estimate the illuminant chromaticity and set the parameters of a color constancy transform. Yang and Maloney [13] used a cue-perturbation method to test the influence of specular highlights, full surface specularity and background color on achromatic settings. With a specularity value of 0.1 (which is high enough that the brightest pixels were close to the illuminant chromaticity) they found a significant influence of the highlight, but no influence of either the full specularity cue or the background.

A consequence of the multiplicative nature of the color transformation imposed by an illuminant change is that cone excitation ratios between pairs of surfaces are approximately preserved. Craven and Foster [14] label the ability to discriminate a change in spectral reflectance and a change in the spectral content of the illumination ‘operational color constancy’. With a stimulus composed of multiple diffuse-Lambertian surfaces under a single illuminant, in which either a subset of surfaces may change or the spectral content of the illuminant may change, Craven and Foster show that observers can perform well when they are required to report which of the changes occurred. Operational color constancy does not require stability of color appearance; simply the correct attribution of image changes to one or other physical origin. We adopted this performance-based measure of constancy in the experiments reported here, but presented only a single curved surface (R(λ)) illuminated by a single illuminant (I(λ)), and measured performance as a function of the specularity of that surface. To understand the information available to the observer to support this discrimination we must describe the stimuli in more detail.

C. Chromatic statistics for specular surfaces

We rendered ‘plastic’ materials as defined by the Ward reflectance model [15], which is a good approximation to most opaque materials other than metals [16]. In this model, a specularity parameter determines the proportion of light reflected in the diffuse component I(λ)R(λ) and the proportion reflected in the specular component I(λ). The mean direction of rays from the specular component is determined by the laws of reflection (i.e. the angle of reflection equals the angle of incidence, where these angles are defined between the ray and the surface normal). The specular reflection is image-forming. If the light source(s) are localised in space, they typically lead to bright (concentrated) highlights in the reflections from the surface. A roughness parameter introduces deviation (scattering) around the mean angle of reflectance, which blurs the image of the source. A zero roughness surface with specularity of 1.0 is a perfect mirror; a surface with specularity and roughness each around 0.1 appears very glossy. The diffuse component is reflected in all directions and its intensity in the image depends on the angle between the surface normal and the illuminant (Lambert’s cosine law).

The chromaticities in an image of a single surface with non-zero specularity, illuminated by a source of a single spectral composition, will lie on a line in color space that joins the chromaticity coordinates of the illuminant (I) with the chromaticity of the wavelength-by-wavelength multiplication of the illuminant and reflectance functions (IR) [1] (Figure 1 illustrates this with stimuli from our experiment). The chromaticities from the diffuse parts of the image, where the scene geometry means that no specular highlight is visible, will lie at one end of this line segment, at the coordinates of IR, although they may be distributed over a range of intensities, based on the angle between the surface and the illuminant. The chromaticities from the most concentrated parts of the specular highlights will be closer to the chromaticity of I, and will have the highest intensity. The specularity of the surface specifies the proportion of light reflected in the diffuse and specular components and therefore determines the maximum extent of this line towards the chromaticity of I. Figure 2 shows the distribution of chromaticities for the most intense pixels in our stimulus images. For surfaces of low specularity, even the most concentrated highlight regions will include light reflected in the diffuse component and so will be a mixture of the chromaticities produced by I(λ) and I(λ)R(λ). Points of the image corresponding to the more scattered regions of the highlight will have chromaticities distributed between the two extremes. In many spaces such as the CIE 1931 xyY color space or the MacLeod-Boynton [17] chromaticity diagram, the locus of chromaticities will project to a straight line in the chromaticity plane, but in spaces designed to be perceptually uniform, such as CIE L*a*b*, the locus may be curved. The curvature of the cloud of points in the intensity direction is determined by the shape and spread of the highlight, which in turn is set by the roughness and curvature of the surface.

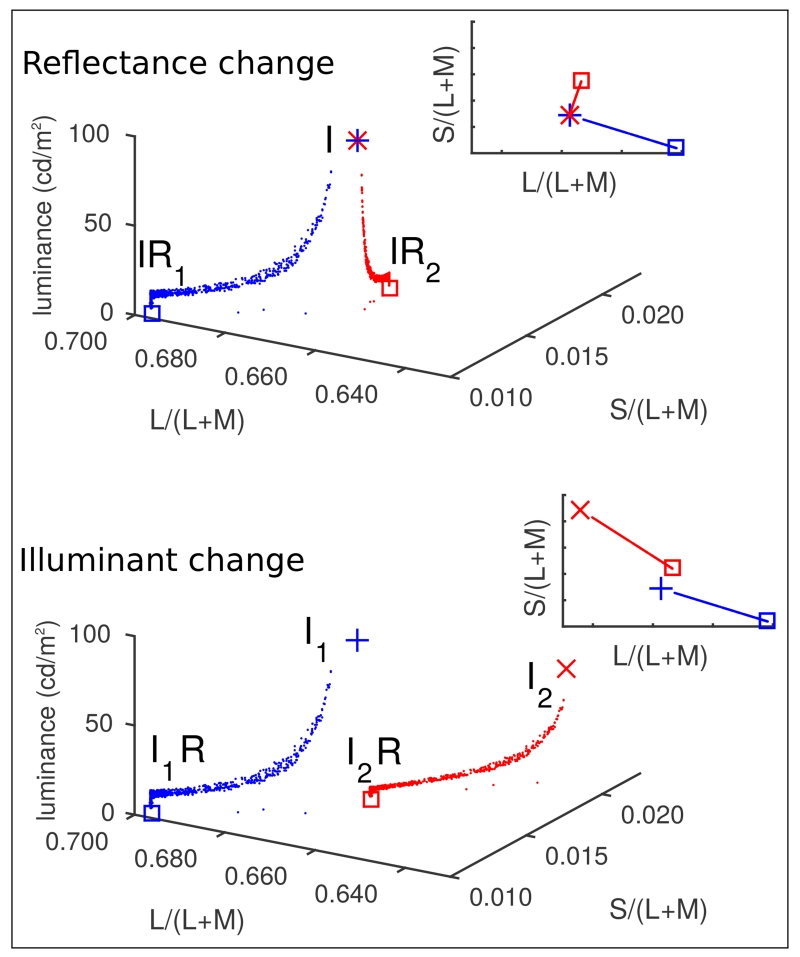
Fig. 1.

Chromaticitic distributions from stimulus images, plotted in the MacLeod-Boynton [17] chromaticity diagram (Constructed using the Stockman and Sharpe cone fundamentals [18, 19] with the S-cone fundamental scaled so that the maximum S/(L+M) value of the spectrum locus is 1 and the L- and M-cone fundamentals scaled so that they sum to V*(λ) [20]). These are taken from animations of spheres with high specularity. The blue dots show chromaticities from the first frame of the animation and the red dots show the chromaticities from the final frame. The top and bottom panels show the conditions to be descriminated in an operational constancy task: (top) a change in the spectral reflectance function of the sphere surface, with no change in the illuminant (I(λ)R₁(λ) to I(λ)R₂(λ)); and (bottom) a change in the spectral power distribution of the illuminant, with no change in the reflectance (I₁(λ)R(λ)toI₂(λ)R(λ)). The red and blue square symbols plot at the chromaticity of the product of the corresponding illuminant and reflectance functions (IR) projected onto the zero-luminance plane, and the + and × symbols plot at the chromaticity of the illuminant I. These I chromaticities have been plotted with reduced luminance since they were never directly viewed, and would be outside the range of the plot axes if plotted at their actual luminances. The 2D insets in each plot show the same chromaticity distributions projected onto an isoluminant plane.

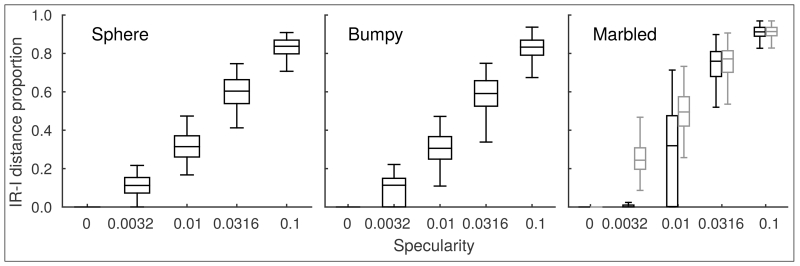
Fig. 2.

Chromaticities of the brightest pixels in our stimulus images, expressed as a proportion of the distance from the chromaticity of the diffuse component (IR) to the chromaticity of the illuminant (I), for the different specularities and conditions used in our experiments. The left panel shows the distributions for all three conditions of Experiment 1, since they share the same chromatic statistics. The centre and right panels show the distributions for the Bumpy and Marbled stimuli from Experiment 2. In (C), the extra series of grey boxes shows the distributions identified by selecting the centre of the highlight, rather than the brightest pixels in the images.

In the present study, we were particularly concerned with observers’ abilities to accurately attribute a change in the stimulus image to either a change in spectral reflectance or a change in the spectral power distribution of the illuminant. In both cases, the chromaticity of the diffuse reflection IR will change. In the case of the illuminant change, I will change as well as IR, whereas in the case of the reflectance change, I will remain the same. With highly specular stimuli, the discrimination could be based on a decision about the most intense pixels: if they are unchanged, the transition is likely to have been a reflectance change. However, at lower specularities, this cue becomes unreliable since even the most intense pixels in the image will contain a mixture of diffuse and specular components, and will therefore change in chromaticity when the reflectance changes. With low specularities, we predict that the full distribution of chromaticities will be important.

For most realistic illuminant and reflectance spectra, an illuminant change will cause similar translations in color space of I and IR. Considering the line connecting IR to I, described by all the chromaticities in the image, this line undergoes a translation during an illuminant change, or a rotation around I during a reflectance change (see Figure 1). For a reflectance change, the parts of the image with the highest intensity (dominated by the specular component and closest to I) will be the ones that change in chromaticity the least, while the parts with lowest intensity (dominated by the diffuse component and closest to IR) will change the most. This is similar to the chromatic convergence cue discussed above for multiple glossy surfaces. For our stimuli, however, only a single line of chromaticities is available at any one instant, so observers must make comparisons of the loci of chromaticities over the course of the transition. The comparison is additionally supported by a correlation between the magnitude of the chromatic change and intensity. There is also a similarity to relational color constancy [9, 21] in which the transition will be classed as an illuminant change if the chromatic relationships between surfaces in a scene are preserved. For our stimuli, however, the range of chromaticities is produced from a single surface, and it is the graded pattern of cone excitations that remains unchanged under an illuminant change but is altered in a reflectance change. Examples of the cone excitations associated with our stimuli are plotted in Figure 3. Under an illuminant change, the relationship between cone signals is described by a multiplicative transform, under a reflectance change it is not. Higher specularity results in a greater spread of chromaticities from IR toward I, which we predict will allow a better estimate of the transformation and result in better discrimination between illuminant and reflectance changes.

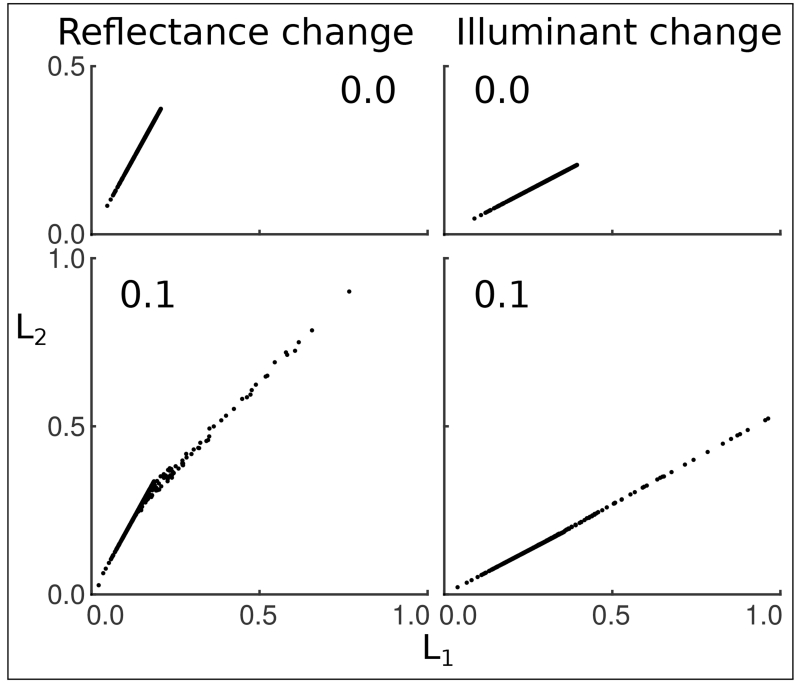
Fig. 3.

Examples of changes in normalized cone excitations elicited by our stimuli. Only excitations of L-cones are shown, but excitations of the M- and S-cones show similar patterns. In each plot, the L-cone excitation from the first frame is plotted on the abscissa and the corresponding excitation from the final frame is plotted on the ordinate. Each dot represents a pixel in the animation. The number inside each plot indicates the specularity of the surface in the stimuli: high specularity in the bottom panels and zero in the top panels. The left-hand-side panels show chromaticities from a reflectance-change stimulus and the right-hand-side panels show chromaticities from an illuminant-change stimulus. Note that the transformation in an illuminant change is multiplicative but, with non-zero specularity, this is not the case for a reflectance change (lower left panel).

D. Spatial structure of scenes with specular surfaces

The discussion so far has concentrated primarily on the chromatic statistics of the scene. However, there is also the suggestion that observers use scene and lighting geometry when estimating the illuminant and judging surface color [22-24] and that, for glossy objects, object shape modulates the information available, affecting color constancy [25]. Observers are sophisticated in their discounting of different contributions to the distal stimulus. For example Xiao and Brainard [26] obtained surface colour matches between matte and glossy spheres and found good compensation for the specular components of the image. Similarly Olkkonen and Brainard [27] found good independence between diffuse and specular components of lightness matches under real-world illumination. With real objects and lights, some studies have shown that three-dimensional scenes allow better color constancy than two-dimensional setups with asymmetric matching [28] or achromatic adjustment [29] but others have found no difference in operational colour constancy [30, 31]. Constancy has been shown to be higher for glossy objects than matte objects and for smooth objects compared to rough objects [32]. These factors have received relatively little attention in much of the classical work on color constancy, which used Mondrian [33] displays in which blocks of color are drawn to simulate diffuse-Lambertian surfaces in a uniform light field, rather than more realistic surfaces and sources. For more complex reflectance models, the scene and lighting geometry is critical.

Whilst the image of the diffuse reflection component lies on the surface of the object, the specular component forms a virtual image that lies in front or behind, depending on the curvature of the surface, and this is critical to the perception of gloss [34]. Separation in depth may help the observer to isolate the highlight from the diffuse reflection and use it as an estimate of the illuminant chromaticity. However, with rendered scenes that contained specular highlights, Yang and Shevell [35] found that viewing the scene with the highlights at their correct depth allowed no more color constancy that viewing the scene with the highlights rendered at the same depth as the surface. They did show an increase in color constancy afforded by binocular stereo presentation of the whole scene, rather than cyclopean viewing, presumably because the stereo presentation provides other information about the scene geometry besides the displacement of the highlights. In the present study, we chose not to render our stimuli with binocular disparity, but instead presented stimuli monocularly to remove conflict between depth cues in the image and cues to the flatness of the display. It is likely that pictorial cues in a monocular image will be of use in interpreting scene and lighting geometry, so performance will be better in images of three-dimensional scenes than in images containing the chromaticity information alone.

Another feature of our stimuli that is unlike those in the majority of color constancy experiments is that at any one instant they contain only a single object. Our intention was to test the sufficiency of specularity alone to support operational color constancy, and multiple surfaces with different diffuse reflectance functions would have provided other sources of information, such as those available in the statistics of Mondrian scenes (e.g. [36]).

E. Rationale

We tested whether single surfaces can support operational color constancy, as a function of the level of specularity. We use synthetic animations of spherical objects lit by point-like sources. In order to simulate physically plausible color changes, these animations were derived from hyperspectral raytraced images of surfaces with known spectral reflectance, and lights with known spectral energy distributions. As stated above, we predicted that with increased specularity, performance would increase. We present two related experiments designed to test the spatio-chromatic relationships that may support observers’ performance. Examples of our stimuli are presented in Figure 4. In the first experiment we compared performance for simple rendered spheres with performance for spatially reorganised images that preserved the chromatic statistics of the simple spheres. Differences in performance between these conditions would rule out any simple model that uses only the available chromaticities, including performance based on the brightest elements. In the second experiment, we compared performance on the simple spheres with performance on bumpy or marbled spheres. Compared to the smooth spheres, bumpy spheres redistribute the spatio-chromatic relationships in the image, but they do so in a way that is consistent with the three-dimensional geometry of a real illuminated object. The marbled spheres introduce intensity noise across the surface of the sphere, reducing the likelihood that the brightest element will locate a chromaticity that is dominated by the specular component, and disrupting the inverse correlation between magnitude of chromatic change and intensity that is present for reflectance changes and absent for illuminant changes.

Fig. 4.

Examples of images from the stimulus animations used in our experiments. The left two columns show the first and final images from an animation of a reflectance change, while the right two columns show the first and final images from an animation of an illuminant change. To aid comparison of these stimulus types, the reflectance and illuminant for the final frame of the reflectance-change example are the same as the reflectance and illuminant for the first frame in the illuminant-change example. Pairs of rows show images for the lowest and highest specularities (0.00 and 0.10 respectively) for the Sphere, Gradient, Scrambled conditions of Experiment 1, and the Bumpy and Marbled conditions of Experiment 2. Note that the color changes in the zero specularity condition are identical for reflectance and illuminant changes, despite the difference in the source of this change. Color reproduction in this figure will not be accurate.

2. METHODS

A. Stimulus generation

Observers viewed animations in which the color of a surface changed, or the color of the light illuminating that surface changed. The stimuli were synthetic, hyperspectral raytraced animations of a sphere in a void, lit by three spherical isotropic illuminant sources at different distances from the sphere. These sources were all assigned the same spectral power distribution in any single frame of an animation. The sphere had a ‘plastic’ bidirectional reflectance function (according to the Ward [15] model) and was assigned one of several spectral reflectance functions and one of five specularity values. The selection of the spectral power and reflectance functions is described later, but all were specified from 400 to 700 nm in steps of 10 nm, and so were divided to 31 wavebands. Five specularity values (as defined by RADIANCE’s plastic definition) were used: zero and four logarithmically spaced values from 10^−2.5 to 10⁻¹. The maximum value of specularity we used (10⁻¹) is a realistic value for a material of this kind [15] and appears glossy. Lower values produced materials with a satin or matte appearance. Importantly, for these low specularities, the light from the brightest points in the image contains a mixture of specular and diffuse components (see Figure 2). The roughness parameter was fixed at 0.15 for all our stimuli. The geometry of the scene was always the same and the camera was placed so that it looked directly at the centre of the sphere, with a large depth-of-field so that all of the sphere appeared in focus. Examples of the resulting images are shown in Figure 4.

Initial images were produced with the RADIANCE Synthetic Imaging System [37] with custom Bash and MATLAB (The Mathworks, Natick, MA, USA) scripts to generate an image for each spectral band. We use similar methods to Heasly et al. [38] and Ruppertsberg and Bloj [39], although we do not use their published code.

We rendered separate hyperspectral images for each frame of the animation, and for each value of specularity used. From these hyperspectral images, relative excitations of the L, M, and S cone classes of the 2° standard observer can be calculated by integrating the product of each pixel’s spectral power distribution by the each of the cone fundamentals. This results in a device-independent cone excitation image that could be converted to an RGB representation for display on our specific hardware, by using spectral measurements of the red, green and blue monitor primaries. Throughout the whole rendering and display procedure, images were stored or processed with 14-bit or greater precision.

An animation consisted of 10 frames in which either the spectral power distribution of the illuminant changed, or the spectral reflectance function changed.

B. Choice of spectral functions

Illuminant spectra were measurements of ‘sunlight’ and ‘skylight’, with CIE 1931 chromaticitiy coordinates of (x, y) = (0.336, 0.350) and (x, y) = (0.263, 0.278) respectively. Reflectance spectra were drawn from a set of 256 spectra obtained from measurements of natural and manmade surfaces [40]. Illuminant or reflectance transitions were specified as linearly ramped mixtures of the initial and final spectra to produce plausible intermediate functions, such as those arising from combinations of pigments or from mixtures of sunlight and skylight. Illuminant changes therefore resulted in chromatic changes that were predominantly aligned with a yellow-blue or blue-yellow direction. Had we chosen reflectance spectra for a given trial without consideration, reflectance changes would not have been subject to the same chromatic restrictions as the illuminant changes. To avoid observers using direction and magnitude of chromatic change as a cue to discriminate illuminant and reflectance changes, we chose pairs of reflectance spectra for the reflectance change trials that produced distributions of the directions and magnitudes of changes in chromaticity coordinates of the diffuse component that were matched to those produced in the illuminant-change trials. Therefore while only the reflectance or illuminant changed in any one animation, the colour change was predominantly in the yellow-blue or blue-yellow direction in both cases. The stimulus chromaticities are summarised in Figure 5. We presented all chosen pairs of reflectances at each level of specularity and in each condition of the experiment. We limited the number of reflectances we chose to 92 so as to limit the total number of different configurations and therefore limit the number of trials in the experiment.

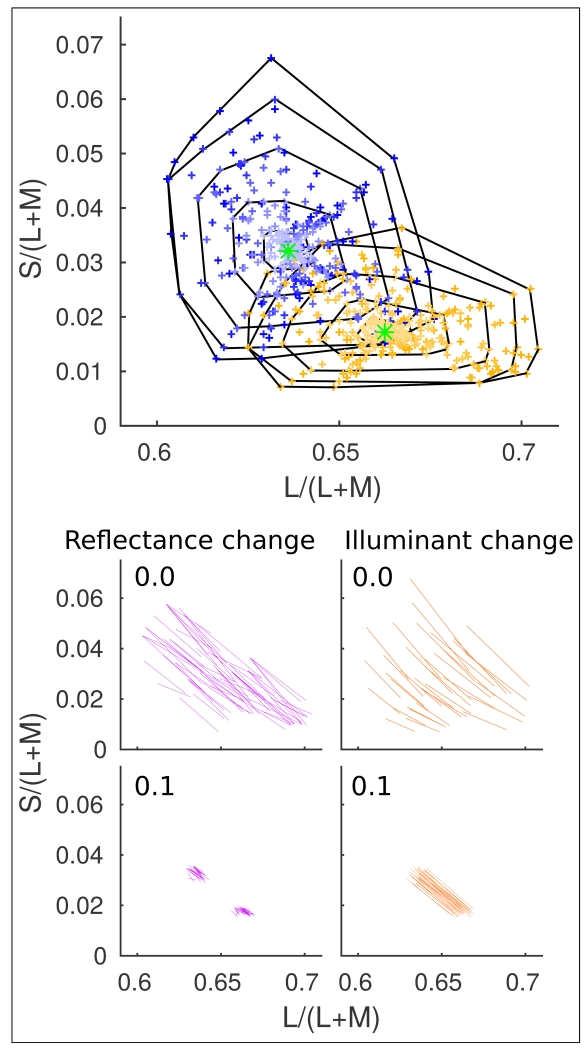
Fig. 5.

Top panel: Chromaticities of the brightest points in the first and final frames of our stimulus animations in the MacLeod-Boynton [17] chromaticity diagram. Yellow + symbols represent surfaces under sunlight, and blue + symbols represent surfaces under skylight. Points with lower saturaton indicate chromaticites with higher specularity. Each of the black polygons encloses chromaticities from stimuli with a particular specularity. The outermost polygon contains surfaces with zero specularity and the smaller polygons enclose stimuli with higher specularities. The chromaticities of the illuminants themselves are indicated by the green symbols in the centres of the corresponding clusters. Lower four panels: Chromaticities visited by the brightest points in our stimulus animations with zero specularity (upper small panels), and specularity = 0.1 (lower small panels) in the same color space as the top panel. Each line connects the chromaticity from the first frame to that of the final frame in one animation. Purple lines (left panels) represent reflectance changes and orange lines (right panels) represent illuminant changes.

C. Image statistics

The primary effect of increasing specularity is to increase the range of chromaticities available in the image, and in particular to extend the locus of chromaticities from the chromaticity of the diffuse component (IR), towards the chromaticity of the illuminant, which is carried in the specular component (I). To summarise the change in chromatic statistics with increasing specularity we extracted the chromaticity of the brightest point in our stimulus images and calculated the distance from IR to this chromaticity as a proportion of the distance between IR and I. Figure 2 shows box-plots of this proportion for the set of stimuli at each level of specularity. At zero specularity, all points in the image share the same chromaticity (IR). As specularity increases, the brightest points take a chromaticity that is increasingly close to the illuminant chromaticity. The intensity of the diffuse reflection, which varied across the reflectance spectra we used in the experiment, will affect the relative weights of I and IR and is the source of the variability seen in the box-plots. For the highest specularity we chose, the majority of images include brightest pixels that contain more than 80% of the illuminant chromaticity, and the box-plot compresses since it is not possible for the image to contain chromaticities beyond I on the IR line.

D. Stimulus presentation

Stimuli were presented on a NEC 2070SB CRT display driven by a Cambridge Research Systems (Rochester, UK) ViSaGe MkII in hypercolor mode, providing chromatic resolution of 14-bits per channel per pixel. The stimuli were 512×512 pixels, which corresponded to approximately 124×124 mm on the monitor or 22°×22° of visual angle at the 1.0m viewing distance. Observers viewed the stimuli monocularly.

The 10 frames of animation were shown at 30 frames per second so that the transition lasted 0.33s. Linnell and Foster [21] found that the ability to detect changes in cone-ratios was best with abrupt changes between illuminants and declined for slower transitions, with most observers reaching chance between 1 and 7 seconds. Our own pilot studies showed that performance was not very sensitive to the speed of the transition. We chose to use a 0.33 sec transition, which allowed us to draw comparisons with data collected for moving stimuli (not reported here), and which appeared smooth whilst using only the number of frames that could be pre-loaded into the display buffer. The first and last frames of the animation were repeated for an additional 0.5 seconds at the beginning and end of the animation, respectively, so that the animation was a transition between two static periods. At any time during the experiment when there was no stimulus being presented, random spatio-temporal luminance noise, with chromaticity and average luminance the same as the whole stimulus set, filled the screen.

Each trial consisted of the presentation of one animation, followed by a 1-second response period. The observer could not give a response until after the animation was complete and had been replaced by the luminance noise. Auditory feedback was given after each trial.

E. Experiment 1

We compared performance in three experimental conditions: Sphere, Gradient, Scrambled. Stimuli in the Sphere condition were simple spheres. Stimuli in the other two conditions were spatial transformations of the simple sphere images. In all cases, the dimensions of the image remained the same, and the transformation was done on the LMS image, before conversion to RGB. Stimuli in all three conditions shared exactly the same chromatic statistics.

For the Gradient condition, the pixels were re-arranged so that they were ordered by intensity (the sum of their L, M and S values), increasing from the top left of the image downwards, and then beginning at the top of the next column to the right and so on, so that the most intense pixels in the image were to the right-hand side.

For the Scrambled condition, the intensity (L+M+S) image of each frame of the animation was extracted, transformed to the Fourier domain (using MATLAB’s two-dimensional FFT routine), and the same randomly generated phase spectrum added to each frame before applying the inverse two-dimensional FFT. The L, M, and S values that were associated with each intensity value in the original image were then given to the corresponding intensity values in the scrambled intensity image. This produced scrambled images containing the same chromaticities as the originals, and the same correlations between intensity and chromaticity change through the animation. Since the random phase offset was applied to all frames of an animation, the spatial structure of the image did not change during the animation. Because the amplitude spectra of the images were not altered, the spatial frequency content of the transformed images was the same as the originals.

Examples of stimuli from each condition are shown in Figure 4, and the relevant chromatic statistics are summarised in 2 (left panel).

F. Experiment 2

We compared performance in two experimental conditions with different modifications to the object’s surface: “bumpy” and “marbled”. The bumpy surfaces were constructed in Blender (Blender Foundation, Amsterdam, The Netherlands) by mapping a procedural noise texture (Blender’s marble texture) to the surface of a sphere as displacement. The resulting surface geometry was then exported to RADIANCE for rendering in place of the simple sphere. The marbled objects had the same surface geometry as the simple spheres. Intensity variation was applied to the surface using a RADIANCE ‘pattern’ that reduced the magnitude of the diffuse reflectance by the same proportion at each spectral band by up to 20%, spatially determined by a volumetric turbulence function evaluated at the surface of the sphere. For each animation, the rotation of the bumpy or marbled sphere about its vertical axis was randomised, so that observers were presented with a different view on each trial. Again, we measured discrimination performance as a function of specularity in the two conditions.

The chromatic statistics in these images share many of the characteristics of the stimuli used in Experiment 1, but are not identical, so predictions based only on chromatic statistics are different for Experiments 1 and 2. For the stimuli in the Bumpy condition, the chromaticities of the brightest pixels at each level of specularity are well matched to the chromaticities of the brightest pixels in Experiment 1. These similarities are summarised in Figure 2. The spatial arrangement of bright elements, and the regularity of chromatic gradients across the image, is however quite different from any of the conditions of Experiment 1. Variation in intensity is carried in a higher spatial frequency range, and there are discontinuities in chromatic gradients. These differences are summarized in Figure 6. For the stimuli in the Marbled condition, the chromaticities of the brightest pixels are a less reliable estimate of the illuminant chromaticity than in Experiment 1. The randomised location of the intensity noise interacts with the geometry of the highlights, so on some trials the most specular region may coincide with a dark region of the marbled pattern, while a diffuse region may coincide with a light region of the marbled pattern, so that the most intense region may in fact be dominated by the chromaticity of the diffuse component. This is most likely to occur at lower specularites, and can be seen in Figure 2 (right panel) where the brightest pixels plot at lower proportions of the IR to I for lower specularities. Since the arrangement of the light sources and the smooth curvature of the sphere determines the regions that are dominated by specularity, it would be possible over trials to select, not the brightest pixel, but the pixel that is in the physical location of the centre of the highlight. In this case, the chromaticity of the selected pixel will be closer to I if the IR component is suppressed by the marbled pattern. The grey box-plots in Figure 2 (right panel) show the distributions of chromaticities obtained via this alternative selection rule.

Fig. 6.

Pseudocolor images to represent the chromatic gradients available in the stimulus images in different conditions of Experiments 1 and 2. The color map represents the chromaticity of the corresponding pixel in the stimulus image, expressed as a proportion of the distance from the chromaticity of the diffuse component (IR) to the chromaticity of the illuminant (I). Green corresponds to (IR) and purple to (I). By removing the intensity variations that are present in the real stimulus images, these plots emphasize the spatial distribution of chromatic statistics.

G. Procedure

There was a total of 2100 unique trials for each observer in Experiment 1 and 1400 unique trials for each observer in Experiment 2. We used equal numbers of illuminant- and reflectance-change trials, equal numbers of trials for each of the five specularities, and equal numbers of trials for each condition. Different conditions were presented in separate sessions, and the trials within each condition were randomly ordered and then divided into four sessions, making twelve sessions of 175 trials in Experiment 1 and eight sessions of 175 trials in Experiment 2. Observers usually ran one session of every condition in a day, and the order of conditions was counterbalanced across days. Before starting the experiment proper, each observer practised with up to four sessions of the Sphere condition only.

H. Observers

Eight observers (1-8) participated in Experiment 1 and four observers (1-4) participated in Experiment 2. All observers had normal color vision (no errors on the HRR plates and a Rayleigh match in the normal range measured on an Oculus HMC-Anomaloskop), and normal or corrected-to-normal visual acuity. Observers 1 and 6 are male; all others are female. Observers 1 and 2 are the authors; observers 3, 4, 5 and 6 were experienced psychophysical observers and had formal education on human color vision (for example, as part of an undergraduate psychology course) but were naïve to the purposes of the experiment; observers 7 and 8 were inexperienced and naïve. For Experiment 2, we selected the observers from Experiment 1 who showed reliable performance in Experiment 1 (a biased sample).

3. RESULTS

A. Experiment 1

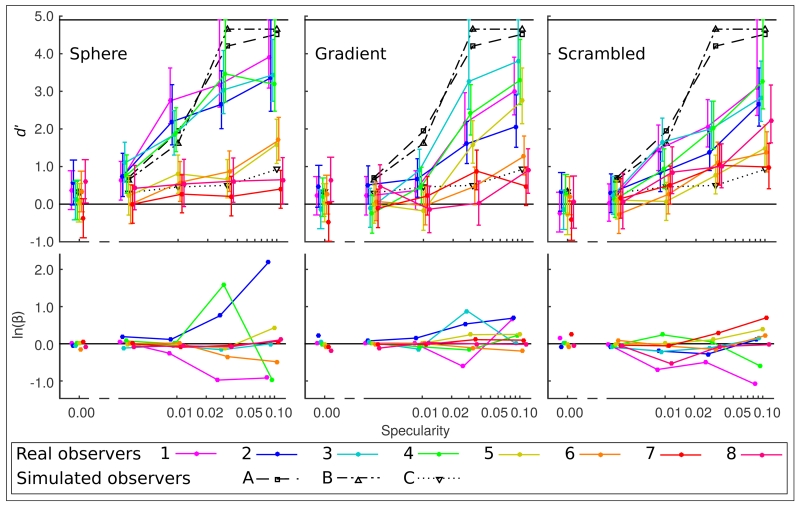
We use d’, a bias-free estimator of sensitivity, to assess performance in discriminating illuminant changes from reflectance changes and ln(β) as an estimate of response bias (positive values indicate a “reflectance change” response). Each estimate of d’ and ln(β) is derived from the 140 trials presented to each observer, at each level of specularity, and in each transformation condition. The top panels in Figure 7 show plots of d’ vs. specularity, with data from each of the eight observers plotted in a different color. Specularity is plotted on a log scale, and performance for zero specularity (matte) stimuli is included at the left-hand side of the graph. The panels below show plots of ln(β) against specularity. In all conditions, performance at zero specularity is near chance (d′ = 0), which suggests that we successfully removed any statistical regularities in the set of illuminants and reflectances that would let observers use the trial-by-trial feedback to classify chromatic changes of the diffuse (matte) component as either reflectance or illuminant changes. The left panels of Figure 7 show data for the Sphere condition. Most observers show some increase in performance with specularity. However the rate of increase of d’ with specularity differs between observers. Some (Observers 1-4) increase to very high performance (d′ ≈ 4) at the highest specularity, whilst for others maximum performance is weaker (d′ ≈ 1). The middle and right panels of Figure 7 show data from the two transformed conditions. Improved performance with increasing specularity is also shown in these conditions, but the maximum dependence on specularity, and the highest d’ reached, is lower than in the Sphere condition. However, in the progression from Sphere to Gradient to Scrambled, performance from different observers becomes increasingly similar, with some suggestion that, while performance from the best-performing observers declines from Sphere to Gradient to Scrambled, performance from the worst-performing observers may increase. A session-by-session analysis for each observer showed no improvements in performance after the practice sessions, indicating that differences between observers do not reflect differences in the time to asymptote.

Fig. 7.

Results from real and simulated observers in Experiment 1. The top panels show d’ at each measured value of specularity, and the lower panels show the corresponding ln(β) values, for the three conditions, Sphere, Gradient and Scrambled. Each real observer is represented by a different colored line (consistent across all plots), as indicated in the key. Error bars show 95% confidence intervals based on the binomial distribution. Each real observer’s data points are slightly horizontally offset by a different amount so that that error bars can be seen, although the specularities used were the same for each observer. The black dashed lines represent the simulated observers A, B and C (see text). The upper solid black line indicates the maximum measurable d’, given the number of trials in the experiment.

The ln(β) plots show that for zero specularity, all observers show neutral response bias, being no more likely to classify the trial as an illuminant-change or as a reflectance-change. As specularity increases, there is a tendency for response bias to increase. For the Sphere condition, this is most marked for Observers 1, 2 and 4, all of whom achieve high performance levels. The other observers maintain a neutral criterion. For the other conditions, there is a lesser effect of specularity, and no marked difference between observers who can do the task and those who cannot.

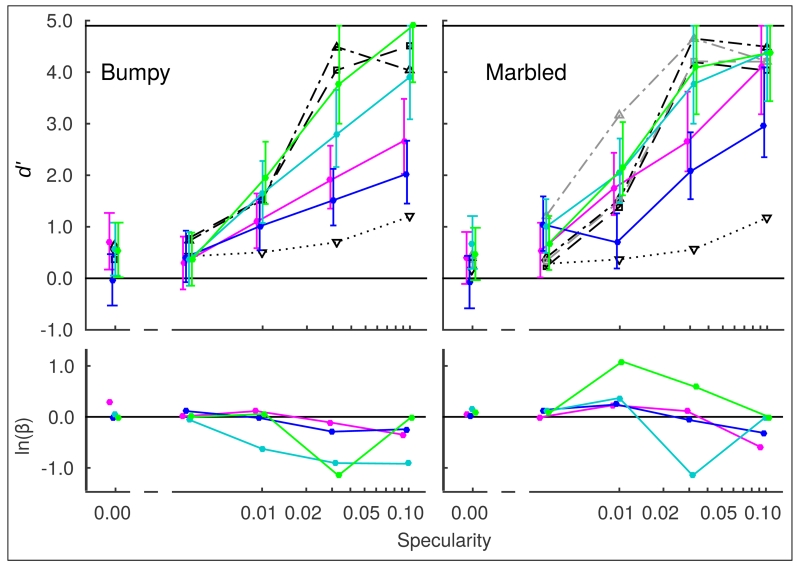
B. Experiment 2

Figure 8 shows plots of d’ and ln(β) vs. specularity, with data from each of the four observers plotted in a different color. Performance is close to chance with zero specularity, and increases systematically as specularity increases. Observers 1 and 2 maintain a neutral response bias. Observers 3 and 4 show some bias at higher specularities, but there is no consistent trend.

Fig. 8.

Results from real and simulated observers in Experiment 2, for the two conditions, Bumpy and Marbled. The formatting of these plots is the same as in Figure 7, and the symbol colors correspond to the same observers. The additional grey lines in the right panel represent the simulated observers A and B using the alternative strategy as described in the text (Section 4B).

The comparison of results between Experiments 1 and 2 requires comparisons of the data presented in Figures 7 and 8. There are two ways to compare the data. Firstly, we could compare the raw d’ values in each experiment. This would include performance differences that are due to the change in availability of chromatic statistics, and performance differences based on the spatial layout of the stimuli. Alternatively, we could compare performance in each experiment to the prediction of a simulated observer who has access to the chromatic information presented in the trials of the experiment. We have chosen the second approach. So, in Figures 7 and 8, we present the performance of our real observers alongside the performance of the simulated observers (described in the following section). For each data point, we provide 95% confidence intervals based on the number of trials that contribute to the estimate. In the Sphere condition of Experiment 1, Observers 1-4 perform at a level very close to that of simulated observers A and B. In the Bumpy condition of Experiment 2 only Observer 4 reaches this level, while the others underperform; in the Marbled condition Observers 1, 3 and 4 are similar to the simulated observers, while observer 2 underperforms. The comparison of results between the Bumpy and Marbled conditions of Experiment 2 again depends on the different availability and reliability of chromatic information in the two cases, summarised in Figure 2 and utilised in the simulated observer models. For Bumpy vs Marbled, paired comparison of each condition (with specularity >0) for each observer indicates higher performance in the Marbled condition (sign test: Z = 2.75, p < 0.05). This is of particular interest, since the chromatic statistics of the brightest pixel predict poorer performance in the Marbled condition.

C. Simulation

As part of our investigation into which cues observers were using to perform the task, we simulated the responses of an observer operating as a supervised-learning multivariate Baysian classifier [41]. We implemented three different simulated observers, operating on three different sets of parameters extracted from the stimulus animations. Our simulated observers were intended to show maximum performance based on optimal extraction of information from the images. Since the difference between first and last frames is most informative for the classification task we used only these frames in the simulations. In each case, the simulated observer ‘saw’ the trials in the same order as the real observers and maintained a perfect history of parameters on which its responses were based. Such accumulation of evidence over trials has been shown previously in human colour constancy performance [42, 43]. We then calculated d’ from the classification performance, as with the real observers. We did this for both Experiments 1 and 2, and the results are plotted on the corresponding results graphs, Figures 7 and 8.

Observer A was intended to simulate an observer who uses the amount of color change, and the color direction of that change, in the highlight (identified as the brightest part of the image, or additionally for Marbled stimuli as the image location corresponding to the highlight) to determine whether the illuminant has changed or not. The observer selects the brightest part of the image in the first frame and in the last frame and calculates the magnitude and direction of the change in chromaticity in the MacLeod-Boynton [17] chromaticity diagram. The histories of magnitudes and directions was maintained separately for illuminant and reflectance changes. On each trial, Observer A’s response was determined by which of the non-parametric multivariate kernel density estimators fitted to these histories gave the highest probability for the observed values. The selection of reflectances discussed in section B was specifically designed to minimise this cue for the zero-specularity stimuli.

Observer B was intended to simulate an observer who attempted to decide which illuminant was present at the start and the end of the animation, separately, based on the chromaticity of the highlight (identified as the brightest part of the image, or additionally for Marbled stimuli as the image location corresponding to the highlight), and respond ‘illuminant change’ if those classifications were different. The histories of S/(L + M) and L/(L + M) chromaticity coordinates of the brightest point in the image were maintained separately for illuminant and reflectance changes. On each trial, Observer B classified the illuminant at the beginning and end of the animation separately, by determining which of the two-dimensional Gaussian probability distribution functions (PDFs) fitted to these histories gave the highest probability for the observed values. The observer’s response was determined by whether or not the two classifications were different.

Observer C was similar to Observer B, but rather than using the brightest points in the first and last frames, Observer C classified the illuminant based on the chromaticity of the global mean in the first and last frames.

Since these simulations are based on the chromaticities in the images and do not take into account the spatial configuration of those chromaticities, predicted performance is identical for all of the transformation conditions in Experiment 1, but differs slightly for the conditions of Experiment 2.

It can be seen in Figures 7 and 8 that the performance of Observers A and B (using the brightest part of the images) improved with increasing specularity, whereas performance of Observer C (using the mean chromaticities) was close to chance level (d′ = 0) and only weakly dependent on specularity. The performances of Observers A and B is very similar in all conditions suggesting that, once the chromaticities of the brightest elements are extracted, decisions based on color change or on discrete classifications at the start and end of the animations can be equally effective. Performance with stimuli in the Marbled condition depends on the strategy for identifying the highlight region. Selecting the brightest pixels is less effective than selecting the region of the image associated with a specular highlight (given the fixed curvature of the spherical stimulus and the fixed geometry of the light sources).

4. DISCUSSION

A. Experiment 1 – simple spheres and individual differences

When Observers 1-4 were asked to distinguish between illuminant changes and reflectance changes in images of isolated spheres, they performed at around chance level when the surface was completely matte, and their performance increased as specularity increased to a level that appeared very glossy. One striking feature of the results of Experiment 1 is that some observers perform much better than others. Despite being given feedback, and the opportunity to practice with stimuli from the Sphere condition, Observers 5-8 used a non-optimal strategy when deciding on their responses. Individual differences in cue-(re)weighting may be important in this task. An analysis of response bias suggests that this is not an explanatory factor in understanding differences between observers. Clearly there are differences between individuals in how they use available cues to perform the task. For the Sphere condition, Observers 5 and 6 show some performance improvement with increasing specularity, whereas Observers 7 and 8 remain close to chance in their classifications for all specularities. At the highest specularities this is surprising, since a simple strategy based on the chromaticity of the brightest pixels (simulated observers A and B) would be highly effective. It is possible that the performance of these observers is dominated by cues that are only marginally informative in this case (e.g. changes in the mean chromaticity such as those used by observer C).

B. Experiment 1 – spatial factors

The transformed stimuli in the Gradient and Scrambled conditions were designed to investigate if and how the spatial structure of the chromatic information was used in the task. The stimuli contained the same pixels as the original spheres but rearranged so that they no longer made a sphere image. We see that performance differed across the three conditions.

The performance of Observers 1-4 (Observers 5-8 are discussed later) depended on specularity in all conditions, but this dependence weakened in the Gradient condition and weakened further in the Scrambled condition. Chromatic variation in the Gradient condition was distributed over a larger spatial scale than in the original Sphere condition, while in the Scrambled condition the phase-scrambling procedure ensured that the spatial scale of chromatic variation was preserved. These differences are illustrated in the pseudocolor images in Figure 6. Differences in performance between the Sphere condition and the Scrambled condition suggest that the availability of spatio-chromatic information (determined, for example, but the sensitivity of the visual system to modulation at different spatial scales) is not the only factor driving performance.

We suggest that, whilst the chromaticities available in all conditions were sufficient to support above chance discrimination, performance improved when those chromaticities were interpreted as a plausible image of an illuminated surface. The images in the Gradient condition are broadly consistent with an illuminated cylinder, whereas the Scrambled condition destroyed the implied three-dimensional structure of the scene. Previous work lends support to this interpretation. Schirillo and Shevell [44] have shown that surfaces arranged to be consistent with an illumination boundary prompt observers to make color matches that compensate for the inferred illumination. When the apparent illuminant edge is removed, even if the ensemble of chromaticities and immediate surround of the test patch are maintained, the matches are altered. A further demonstration of the importance of perceptual organisation on surface color judgement is provided by Bloj, Kersten and Hurlbert [45]. In their experiment, magenta paper on one side of a concave folded card reflects pinkish light onto the other half of the card, which is covered in white paper. When observers viewed the folded card in the appropriate perspective their color judgements compensate for the mutual illumination, but when viewing the card via a pseudoscope (so it appears convex) observers judged the white card to be pale pink. The consensus from these results is that the spectral and geometric properties of inferred illumination feed into color perception at an early stage.

In a real scene, the image of the specular highlight would appear behind that of the diffuse surface. This would be possible to simulate with two renderings from different viewpoints, and stereoscopic presentation, but in our experiment we used only one image. Observers judge surfaces to be glossy when specular highlights have the correct relative disparity [34] although then do not always use disparity cues as expected when judging shape [46]. The influence of disparity cues on performance in our task is and empirical question, and one that is yet to be answered.

Interestingly, for Observers 5-8 performance was worst in the Sphere condition, and increased in the Gradient and Scrambled conditions. In the Gradient condition Observer 8 was performing as well as Observers 1-4, and in the Scrambled condition, the difference between the two groups of observers is much less noticeable. For a color constant observer that perceptually discounts the illuminant, the illuminant-change trials will appear stable (so neither reflectance nor illuminant will appear to have changed). The reflectance-change trials will present a change in the relationship between the diffuse component and the highlight (similar to the pop-out experienced for reflectance changes in the experiments reported by Foster et al. [47]). With only two dominant chromaticities in the scene, it may be ambiguous to determine which has changed. Under this speculative interpretation, performance is predicted to be poor in the Sphere condition, which presents the best opportunity for constancy of surface reflectance accompanied by perceptual discounting of the illuminant. It is possible that these observers are relying on the global mean of the image to make their judgments.

C. Experiment 2

Observers 1-4 show improved performance with increasing specularity in both conditions of Experiment 2. These results suggest that the effect found with simple spheres generalises to more complex surfaces.

In the Bumpy condition the chromatic statistics available in the image are very similar to those in all three conditions of Experiment 1, as summarised by the box-plots in Figure 2. However, the spatial locations of the highlights are randomised by the local variation in surface curvature. The 3D geometry of the point-like light sources is more difficult to infer, but the highlights give strong (but potentially ambiguous [48]) cues to surface shape.

Since we presented the sphere in a different random orientation on each trial, the locations of the highlights in the image varied from trial-to-trial, as they had in the Scrambled condition, but not in either the Sphere or Gradient conditions, of Experiment 1. The Bumpy and Scrambled conditions therefore share some unpredictability but they differ in the spatial scale of the chromatic gradients imposed by the transitions from diffuse to specular regions of the image. These differences are apparent in the pseudocolor images of Figure 6, where it is clear that the chromatic gradients are steeper and more localised in the Bumpy condition. For Observers 3 and 4, very high performance is maintained in the Bumpy condition, but performance in the Bumpy condition is worse than in the Sphere condition for Observers 1 and 2, and approaches the level obtained in the Scrambled condition. This reduction in performance may be due to the reduction in predictability of the these stimuli from trial to trial.

In the Marbled condition, the achromatic variation in surface reflectance has very little effect on the spatio-chromatic gradients in the image (see Figure 6), but significantly disrupts some of the statistical regularities that are available in the stimuli in all conditions of Experiment 1. In particular, the marbling introduces intensity noise that disrupts the correlation between magnitude of chromatic change and intensity that is a signature of reflectances changes (see Figure 1), and additionally breaks the correspondence between the brightest pixel and a chromaticity that is dominated by the specular component. This effect of the marbling on the chromatic statistics is clear in the box-plots of Figure 2C showing the proportion of distance along the I to IR vector that is sampled by the brightest pixel. At high specularities, the intensity of the specular component dominates, and the brightest pixel locates the chromaticity of the specular component, as effectively as in the other conditions. However, at mid-specularities, the brightest pixel may be located on a light region of the marbled surface, and may not correspond with the location of the specular component, selecting instead a chromaticity more heavily dominated by the diffuse component. Interestingly, however, the performance of all four observers was very high in this condition, suggesting that disruption of chromatic statistics with intensity noise (for the single pattern contrast we used), as well as unpredictability from trial-to-trial in the spatial location of the most useful chromaticities, had less effect on performance than the spatial disruption of chromatic gradients (for the level of bumpiness we used).

D. Comparison with the simulated observers

Our simulated observers, A, B and C based their classifications on low-level chromatic statistics available in the images. Observers A and B rely on the chromaticities of the brightest pixels; Observer C relies on the mean chromaticity of the image. In Experiment 1, the four observers who perform better than the others (Observers 1-4) perform at a similar level to Observers A and B for the Sphere condition of Experiment 1, in all but the highest specularities. In the Gradient and Scrambled conditions, the real observers fall well below the performance of Observers A and B, particularly at high specularities, despite having access to the same chromatic information for the brightest pixels. The observers who are performing at the lowest levels (Observers 7 and 8) make classifications that are consistent with the level of discrimination that would be obtained using the mean image chromaticity.

In Experiment 2, Observer 4’s performance on the Bumpy stimuli follows that of Observers A and B, whereas the others fall somewhat below this level. In the Marbled condition, performance is good for all Observers 1-4, and at low specularities exceeds that predicted by Observers A and B. This improvement with marbled stimuli is a curious result and deserves some discussion. If performance were simply based on the chromaticity of the brightest pixels, there should be an advantage for Bumpy stimuli over Marbled, since the box plots in Figure 2 show that for the lower specularity levels, the brightest pixels are closer to the illuminant chromaticity for the Bumpy stimuli than for the Marbled stimuli. The relative improvement in the Marbled case is predicted by an alternative strategy, namely that observers base their judgement on the spatial region of the image that they have learned is associated with a specular highlight (given the fixed curvature of the spherical stimulus and the fixed geometry of the light sources). The I to IR proportions of these values are shown in the grey box-plots in Figure 2C, and the corresponding performances of Observers A and B are shown in grey on Figure 8. This alternative strategy might explain the trend for Observers 1-4 to out-perform the ideal brightest-pixel observer at low specularities in the Marbled case. It is a strategy that is consistent with the idea that observers are sensitive to the perceptual organisation of surfaces and the lights that illuminate them, rather than making a decision based on simple chromatic statistics in the image.

E. Conclusion

We have shown that observers are, in general but to varying degrees, able to use low levels of surface specularity to discriminate between illuminant changes and reflectance changes. We tested observers’ performances in the absence of other cues by using rendered scenes that contained only a single isolated surface. Parametric testing of the effect of the specularity parameter in the Ward reflectance model shows an approximately linear increase in d’ with logarithmic increases in specularity. While it seems that the changes in chromatic statistics of the image that accompany increases in specularity allow reliable performance in this task by themselves, performance is better when observers are presented with a plausible image of a glossy object. It is possible that the visual system parses the complex spatial arrangement of diffuse and specular reflections in an image and can use them to accurately attribute image changes to either changes in reflectance or illumination.